Abstract
Two novel and exciting avenues of neuroscientific research involve the study of task‐driven dynamic reconfigurations of functional connectivity networks and the study of functional connectivity in real‐time. While the former is a well‐established field within neuroscience and has received considerable attention in recent years, the latter remains in its infancy. To date, the vast majority of real‐time fMRI studies have focused on a single brain region at a time. This is due in part to the many challenges faced when estimating dynamic functional connectivity networks in real‐time. In this work, we propose a novel methodology with which to accurately track changes in time‐varying functional connectivity networks in real‐time. The proposed method is shown to perform competitively when compared to state‐of‐the‐art offline algorithms using both synthetic as well as real‐time fMRI data. The proposed method is applied to motor task data from the Human Connectome Project as well as to data obtained from a visuospatial attention task. We demonstrate that the algorithm is able to accurately estimate task‐related changes in network structure in real‐time. Hum Brain Mapp 38:202–220, 2017. © 2016 Wiley Periodicals, Inc.
Keywords: functional connectivity, dynamic networks, real‐time, streaming penalized optimization, neurofeedback
INTRODUCTION
The notion that the brain is a network consisting of spatially distributed and functionally connected regions is well established in neuroimaging [Bullmore and Sporns, 2009]. Until recently, the vast majority of studies involving functional connectivity assumed the underlying networks were static. As a result, a single underlying network was typically estimated and assumed to summarize the connectivity structure.While such an approach reliably recovers intrinsic functional connectivity networks that exhibit satisfactory intra‐indiviudal stability across scans [Pinter et al, 2016; Song et al, 2012], such a simplified assumption has been strongly contested in recent years [Chang and Glover, 2010; Sakoğlu et al., 2010]. There is a growing body of evidence to suggest that functional connectivity networks are in fact time‐varying (see Hutchison et al. [2013] and references therein). The study of so called dynamic functional connectivity, therefore, constitutes a rapidly emerging and novel avenue of neuroscience research. Since its inception, the study of dynamic connectivity has lead to crucial insights into the functional organization of the human connectome both during rest [Allen et al., 2014] as well as during cognitive tasks [Elton and Gao, 2014; Fornito et al., 2012; Monti et al., 2015]. From a technical perspective, a wide range of statistical methodologies have been used to study dynamic connectivity. These range from the use of change point detection [Cribben et al., 2012; Robinson et al., 2010] to regularized likelihood methods [Allen et al., 2014; Monti et al., 2014], state‐space models [Robinson et al., 2015], projection‐based methods such as principal component analysis [Leonardi et al., 2013] and linear discriminant analysis [Monti et al., 2015]. However, all of the aforementioned methods have focused on studying connectivity in an offline setting; that is to say that networks are only estimated once all data has been collected and preprocessed. In this work, we focus on the related but fundamentally different challenge of accurately estimating functional connectivity networks in real‐time.
The study of fMRI in real‐time is another rapidly expanding avenue of neuroscience research. A dominant application of real‐time (rt) fMRI has been centered around neurofeedback [deCharms, 2008; Weiskopf, 2012] in which participants learn to modulate blood‐oxygen‐level dependent (BOLD) activity within a specified brain region. However, such region of interest (ROI)‐based neurofeedback does not take into consideration the above mentioned notion of the brain as functionally connected network [Bressler and Menon, 2010; Ruiz et al., 2014; Sporns et al., 2004]. Another pertinent application of rt‐fMRI is in real‐time brain decoding [LaConte, 2011]. Such methods use multivariate classification techniques to predict brain states “on the fly” based on BOLD measurements across a large number of nodes (voxels or regions). To date, techniques such as support vector machines [LaConte et al., 2007] and neural nets [Eklund et al., 2009] have been used. It is reasonable to suggest that the performance of these classification algorithms could be further boosted by providing them with additional information relating to functional connectivity. It, therefore, follows that the next frontier for rt‐fMRI studies involves accurately estimating brain connectivity in real‐time. So far there have been only a limited number of studies focusing on estimating functional connectivity in real‐time and their primary focus has been on neurofeedback [Koush et al., 2013, 2016; Liew et al., 2015; Ruiz et al., 2014; Zilverstand et al., 2014]. A limitation of those studies however is that it only provides real‐time neurofeedback based on changes in connectivity between a very small number of ROIs. Methods that would allow instantaneous neurofeedback based on entire networks could drastically boost the relevance of such an approach by providing a far richer description of the brain state as can be achieved with state‐of‐the‐art offline methods.
Developing novel methodologies to estimate functional connectivity between many ROIs in real‐time although presents considerable theoretical and practical challenges. First, due to the nature of neurofeedback the resulting time series are expected to vary significantly over time. The accurate estimation of dynamic functional connectivity networks in an offline setting is a difficult problem in its own right and has recently received considerable attention [Allen et al., 2014; Davison et al., 2015; Monti et al., 2014, 2016]. In this work, we look to address this issue by extending recently proposed methods from the offline domain to the real‐time domain. Second, due to potentially rapid changes that may occur in a subjects' functional connectivity the proposed method must be both computationally efficient as well as highly adaptive to change. To satisfy the latter, the proposed method must be capable of accurately estimating functional connectivity networks using only a reduced (and adequately re‐weighted) subset of current and past observations.
To address these challenges, we first propose the use of exponentially weighted moving average (EWMA) models [Lindquist et al., 2014] as well as more general adaptive forgetting techniques. This decision is motivated by the superior statistical properties of such approaches as well as the need to ensure that the proposed methods are as adaptive as possible. Through several simulations, we provide exhaustive evidence to suggest such methods should be preferred to sliding windows. We then extend the recently proposed Smooth Incremental Graphical Lasso Estimation (SINGLE) algorithm [Monti et al., 2014] to the real‐time scenario. Here, functional relationships between pairs of nodes are estimated using partial correlations (as opposed to Pearson's correlation) as they have been shown to be better suited to detecting changes in network structure [Smith et al., 2011; Marrelec et al., 2009]. The rt‐SINGLE algorithm encourages two desirable properties in estimated functional connectivity networks: sparsity and temporal homogenity. We are able to re‐cast the estimation of a new functional connectivity network as a convex optimization problem which can be quickly and efficiently solved in real‐time. In addition to an extensive set of simuations, we also apply the proposed method to two different fMRI data sets: motor task data from the Human Connectome Projects (HCPs) as well as data obtained from a visuospatial attention task. We demonstrate that the algorithm is able to accurately estimate task‐related changes in network structure in real‐time and discuss important applications. To our knowledge, this is the first work to propose and validate estimating functional connectivity networks consisting of a high number of ROIs in real‐time.
METHODS
In this section, we introduce and describe the proposed method. We begin by defining notation in Notation section, then a high‐level overview of the proposed method is provided in Overview of Proposed Method section followed by a detailed description of the proposed method in First Step: Real‐Time, Adaptive Covariance Estimation and Second Step: Real‐Time Network Estimation sections. Finally, the selection of relevant parameters is discussed in Parameter Tuning section.
Notation
We assume we have access to a stream of multivariate fMRI measurements across p nodes where each node represents a ROI. We write to denote the BOLD measurements at the time point across p ROIs; thus corresponds to the BOLD measurement of the ith node at time t. In this work, we are interested in sequentially using all observations up to and including to recursively learn the underlying functional connectivity networks. At time t + 1 it is assumed we receive a new observation , which we use to update our network estimates accordingly. Throughout the remainder of this manuscript, it is assumed that each follows a multivariate Gaussian distribution, , where both the mean and covariance structure are assumed to vary over time.
The functional connectivity network at time t can be estimated by learning the corresponding precision (inverse covariance) matrix, . Such approaches have been used extensively in neuroimaging applications [Ryali et al., 2012; Smith et al., 2011; Varoquaux et al., 2010;] and have also recently been proposed to estimate time‐varying estimates of functional connectivity networks [Allen et al., 2014; Cribben et al., 2012; Monti et al., 2014]. Here, encodes the partial correlations as well as the conditional independence structure at time t. We then encode as a graph, , where the presence of an edge implies a non‐zero entry in the corresponding entry of the precision matrix [Lauritzen, 1996].
Therefore, our aim is to estimate an increasing sequence of functional connectivity networks, where each captures the functional connectivity structure at the tth observation.
Overview of Proposed Method
The objective of this work is to obtain estimates of functional connectivity networks which display the following properties:
Real‐time: first and foremost, the primary objective of this work is to estimate functional connectivity networks in real‐time. It follows that in any rt‐fMRI application it is crucial that estimated functional connectivity networks are available in a timely manner.
Adaptivity: we are particularly interested in the changes caused by the direct interaction with subjects while they are in the scanner. As such, it is crucial to be able to rapidly quantify changes in functional connectivity structure once these have occurred. The need for highly adaptive estimation methodologies is further exacerbated by the lagged nature of the hemodynamic response function, where changes in functional measurements typically occur 6 s after performing a task [LaConte et al., 2007].
Accuracy: we also wish to accurately estimate network structure over time. This involves both the accurate estimation of network connectivity at each time point as well as the temporal evolution of pairwise relationships between nodes over time. That is to say, estimated networks should provide accurate representations of the true underlying functional connectivity structure at any point in time as well as accurately describing how networks evolve over time.
The task of estimating in real time can be broken into two independent steps. First, an updated estimate of the sample covariance, , is calculated. We propose two methods with which an adaptive and accurate estimate of can be obtained: EWMA models and adaptive forgetting (discussed in First Step: Real‐Time, Adaptive Covariance Estimation section). In a second step, the corresponding precision matrix, , is estimated given the sample covariance. This is achieved by extending the recently proposed SINGLE algorithm [Monti et al., 2014] from the offline to the real‐time domain (discussed in Second Step: Real‐Time Network Estimation section).
First Step: Real‐Time, Adaptive Covariance Estimation
The estimation of functional connectivity networks is fundamentally a statistical challenge which is often studied by quantifying the pairwise correlations across various ROIs [Friston, 1994]. Such approaches correspond directly to estimating and studying the covariance structure. When the functional time series is assumed to be stationary, this coincides with studying the sample covariance matrix for the entire dataset. However, in the case of rt‐fMRI studies we are faced with data that is inherently non‐stationary. Moreover, we have the additional constraint that data arrives sequentially over time, implying that information from new observations must be efficiently incorporated to update network estimates.
In this section, we describe how adaptive estimates of the sample covariance can be obtained in real‐time via the use of EWMA models or adaptive forgetting techniques.
Sliding windows and EWMA models
Arguably the dominant approach used to obtain adaptive functional connectivity estimates involves the use of sliding windows [Hutchison et al., 2013] and this also holds true in the rt‐fMRI setting [Esposito et al., 2003; Gembris et al., 2000; Ruiz et al., 2014; Zilverstand et al., 2014]. Such methods are able to obtain adaptive functional connectivity estimates in real‐time by only considering a fixed number of past observations, defined as the window. Using only the observations within the predefined window, a local (i.e., adaptive) estimate of functional connectivity is obtained. A sliding window may be used to obtain a local estimate of the sample covariance, , at time t as follows:
| (1) |
where is the mean of all observations falling within the sliding window and parameter h is the length of the sliding window.
A natural extension of sliding windows is the use of an EWMA, first introduced by Roberts [1959]. Here, observations are re‐weighted according to their chronological proximity. The rate at which past information is discarded is determined by a fixed forgetting factor, . In this way, EWMA models are able to give greater importance to more recent observations thus increasing the adaptivity of the resulting algorithm. Moreover, as described in Lindquist et al. [2014], these methods enjoy superior statistical properties when compared to sliding window algorithms. EWMA models thereby provide a conceptually simple and robust method with which to handle a wide range of non‐stationary processes. They are also particularly well suited to the real‐time setting as we discuss below.
For a given forgetting factor, , the estimated mean at time t can be recursively defined as:
| (2) |
where is a normalizing constant which is calculated as:
| (3) |
The sample covariance at time t is subsequently defined as1:
| (4) |
| (5) |
From Eqs. (2) and (4), we note that past observations gradually receive less importance. This is a contrast to sliding windows, where all observations within the window receive equal weighting. It follows that the choice of parameter r determines the rate at which information from previous observations is discarded and is directly related to the adaptivity of the proposed method. This can be seen by considering the extreme cases where r = 1. Here, we have that and consequently that and correspond to the sample mean and covariance estimated in an offline setting (using all observations up to time t). As a result equal importance is given to all observations, leading to reduced adaptivity to changes. As the value of r is reduced, greater importance is given to more recent observations resulting in an increasingly adaptive estimate. Of course, as the value of r decreases the estimated mean and covariance become increasingly susceptible to outliers and noise. The choice of r therefore constitutes a trade‐off between adaptivity and stability. Much like the length of the sliding window, h, the choice of r essentially determines the effective sample size used to estimate both and . Therefore, the same logic applies when choosing both r and h: the value must be sufficiently large so as to allow robust estimation of the sample covariance without becoming too large [Sakoglu et al., 2010].
Adaptive forgetting models
It is important to note that for any non‐stationary data the optimal choice of both r and h may depend on the location within the dataset. By this, we mean that in the proximity to a change‐point it would clearly be desirable to have smaller choice of h and r; thereby reducing the influence of old, irrelevant observations. Whereas within a locally stationary region, we wish to have a larger choices of h and r to effectively learn from a wide range of pertinent observations. This concept is demonstrated pictorially in the top panel of Figure 1. In the case of real‐time fMRI, we inherently expect the statistical properties of a subject's functional connectivity networks to vary depending on a wide range of factors (e.g., varying task demands). Therefore, the choice of a fixed window length, h, or forgetting factor, r, may be inappropriate.
Figure 1.
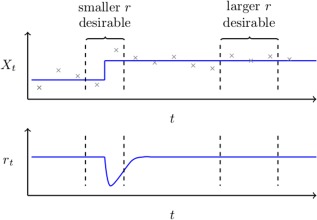
Top: Measurements of a non‐stationarity univariate random variable, , are shown in grey together with the true mean in blue. This figure serves to highlight how the optimal choice of a forgetting factor or window length may depend on location within a dataset. It follows that in the proximity of the change‐point we wish to be small in order for it to adapt to change quickly. However, when the data is itself piece‐wise stationary, we wish for to be large in order to be able to fully exploit all relevant data.
Bottom: An illustration of how an ideal adaptive forgetting factor would behave; decreasing directly after a change occurs and quickly recovering thereafter. [Color figure can be viewed at http://wileyonlinelibrary.com.]
To address this issue, we propose the use of an adaptive forgetting methodology [Haykin, 2008]. This corresponds to a selection of methods where the magnitude of the forgetting factor is adjusted directly from the data in real‐time. This is achieved by approximating the derivative of the likelihood for every new observation with respect to the forgetting factor. We are, therefore, able to update the forgetting factor in a stochastic gradient descent framework [Bottou, 2004]. As a result, the value of the forgetting factor has a direct dependence on the time index, t. To make this relationship explicit, we write to denote the adaptive forgetting factor at time t. The bottom panel of Figure 1 provides an illustration of desirable behavior for an adaptive forgetting factor. We note that immediately after a change occurs the forgetting factor drops. This helps discard past information which is no longer relevant and gives additional weighting to new observations. Moreover, it is also important to note that in the presence of piece‐wise stationary data the value of the adaptive forgetting factor increases, allowing for a larger number of observations to be leveraged and yielding more accurate and stable estimates.
Moreover, the use of adaptive forgetting also provides an additional monitoring mechanism. By considering the estimated value of the forgetting factor at any given point in time, we can gain an understanding as to the current degree of non‐stationarity in the data [Anagnostopoulos et al., 2012]. This follows from the fact that the estimated forgetting factor quantifies the influence of recent observations on the sample mean and covariance. Therefore, large values of are indicative of piece‐wise stationarity whereas small values of provide evidence for changes in the network structure.
To effectively learn the forgetting factor in real‐time, we require a data‐driven approach. One popular solution is to empirically measure performance of current estimates by calculating the likelihood of incoming observations. In this way, we are able to measure the performance of an estimated mean, , and sample covariance, , when provided with unseen data. This provides the basis on which to update our choice of forgetting factor. Under the assumption that all observations follow a multivariate Gaussian distribution, this likelihood of a new observation is given by:
| (6) |
While it would be possible to maximize using a cross‐validation framework in an offline setting, such an approach is challenging in a real‐time setting. Cross‐validation approaches typically consider general performance over many subsets of past observations; therefore, incurring a high computational cost. Moreover, due to the highly autocorrelated nature of fMRI time series, splitting past observations into subsets is itself non‐trivial. Here, we build on the work of Anagnostopoulos et al. [2012] and use adaptive forgetting methods to maximize this quantity in a computationally efficient manner. This is achieved by approximating the derivative of with respect to . This derivative can subsequently be used to update in a stochastic gradient ascent framework [Bottou, 2004].
From Eqs. (2), (4), and (5), we can see the direct dependence of estimates and on a fixed forgetting factor r. This suggests that the likelihood is itself a function of the forgetting factor, allowing us to calculate its derivative with respect to r as follows:
| (7) |
where have written A′ to denote the derivative of A with respect to r (i.e., ). Full details are provided in the Supporting Information A.
Given the derivative, , we can subsequently update our choice of forgetting factor using gradient ascent:
| (8) |
where η is a small step‐size parameter. Equation (8) serves to highlight the strengths of adaptive forgetting; by calculating we are able to learn the direction along which maximizes the log‐likelihood of unseen observations. It follows that if is positive, should be increased, while the converse is true if is negative. Moreover, in calculating we also learn a magnitude. This implies that all updates in Eq. (8) will be of a different order of magnitude. This is fundamental as it allows for rapid adjustments in the presence of abrupt changes together with small adjustments in the presence of gradual drifts.
Finally, once has been calculated, we are able to learn estimates and using the same recursive Eqs. (2), (3), (4), (5) with the minor amendment that the effective sample size, is calculated as:
| (9) |
Second Step: Real‐Time Network Estimation
To ensure estimated networks provide an accurate representation of true functional connectivity networks, we encourage two properties in estimated functional connectivity networks: sparsity and temporal homogenity.
Sparsity and temporal homogenity
While functional connectivity networks are theorized to have evolved to achieve high efficiency of information transfer at a low connection cost [Bullmore and Sporns, 2009], the main motivation behind the introduction of sparsity here is based on statistical considerations. Formally, the introduction of sparsity ensures the estimation problem remains feasible when the number of relevant observations falls below the number of parameters to estimate [Michel et al., 2011; Ryali et al., 2012]. In the presence of rapid changes, the number of relevant observations falls drastically. In such a scenario, sparse methods are able to guarantee the accurate estimation of functional connectivity networks without compromising the adaptivity of the proposed method.
The second property we wish to encourage is temporal homogeneity; from a neuroscientific perspective, we expect changes in functional connectivity structure to occur predominantly when paradigm changes occur (e.g., a subject begins performing a different task). Thus, we expect network structure to remain constant within a neighborhood of any observation but to vary over a longer period of time. We, therefore, encourage sparse innovations in network structure over time, ensuring that a change in connectivity is only reported when strongly substantiated by evidence in the data. Finally, real‐time performance is achieved by casting the estimation as a convex optimization problem which can be efficiently solved.
Algorithmic details of real‐time SINGLE
In this section, we describe how we can extend the SINGLE algorithm [Monti et al., 2014] in such a manner that we can obtain an estimated precision matrix that is both sparse and temporally homogeneous in real time.
Given a sequence of estimated sample covariance matrices , the SINGLE algorithm is able to estimate corresponding precision matrices, , by solving the following convex optimization problem:
| (10) |
The first sum in Eq. (10) corresponds to a likelihood term while the remaining terms, parameterized by and , respectively, enforce sparsity and temporal homogeneity constraints. Estimated precision matrices, , therefore balance a trade‐off between adequately describing observed data and satisfying sparsity and temporal homogeneity constraints.
However, in the real‐time setting, a new is constantly obtained implying that the dimension of the solution to Eq. (10) grows over time. It follows that iteratively re‐solving Eq. (10) is both wasteful and computationally expensive. In particular, valuable computational resources will be spent estimating past networks which are no longer of interest. To address this issue, the following objective function is proposed to estimate the functional connectivity network at time t:
| (11) |
where corresponds to the estimate of the precision matrix at time t − 1 and is assumed to be fixed. The proposed real‐time SINGLE (rt‐SINGLE) algorithm is thus able to accurately estimate by minimizing Eq. (11)—in doing so the proposed method must find a balance between goodness‐of‐fit and satisfying the regularization constraints. The former is captured by the likelihood term:
| (12) |
and provides a measure of how precisely describes the current estimate of the sample covariance, . The latter two terms of the objective correspond to regularization penalty terms:
| (13) |
The first of these, parameterized by , encourages sparsity while the second, parameterized by , determines the extent of temporal homogeneity. By penalizing changes in functional connectivity networks, the second penalty encourages sparse innovations in edge structure over time. As a result, network changes are only reported when heavily substantiated by evidence in the data. Moreover, the addition of regularization of this form serves to vastly reduce the number of parameters. Such an approach is often advocated in neuroimaging studies [Ryali et al., 2012; Varoquaux and Craddock, 2013]. Further details of the proposed optimization algorithm are discussed in Supporting Information B.
Parameter Tuning
Parameter estimation is challenging in the real‐time setting. Approaches such as cross‐validation, which are inherently difficult to implement due to the non‐stationarity of the data, are further hampered by the limited computational resources. As an alternative, information theoretic approaches such as minimizing the AIC or BIC may be taken but these too may incur a high computational burden. In this section, we discuss the three parameters required in the proposed method and provide a clear interpretation as well as a general overview on how each should be set.
In this work, we advocate the use adaptive forgetting factors which provide a more elegant and flexible solution when compared to sliding window approaches or EMWA with fixed forgetting. These methods designate the choice of to the data. As a result, only the stepsize parameter, η, must be specified. The choice of η in this context can be interpreted as a step‐size parameter for tuning the forgetting factor in a stochastic gradient descent paradigm [Bottou, 2004]. As a result, the effect of parameter η can be intuitively understood. Selecting η to be too large will result in estimates of which are volatile and potentially dominated by noise. Conversely, selecting small η may lead to slow convergence. In practice, we find that selecting η between 0.001 and 0.05 is adequate.
Parameters and enforce sparsity and temporal homogeneity respectively. The choice of these parameters affects the degrees of freedom of estimated networks, suggesting the use of information theoretic approaches such as AIC. However, in a real‐time setting, choosing and in such a manner presents a computational burden. As a result, we propose two heuristics for choosing appropriate values of and , respectively. One potential approach involves studying a previous scan of the subject in question. If this is available, then the regularization parameters may be chosen by minimizing AIC over this scan. Alternatively, the burn‐in phase may be used to choose adequate parameters. Such an approach would involve choosing and which minimized AIC over the burn in period. Moreover, it is worth noting that tuning and adaptively in a similar manner to the forgetting factor presents theoretical and computational challenges due to the non‐differentiable nature of the regularization penalties.
SIMULATION STUDY
In this section, we evaluate the performance of the rt‐SINGLE algorithm through a series of simulation studies. The purpose of our simulation is twofold. First, we look to demonstrate the properties of adaptive forgetting methods. As such, throughout this section we compare results for the rt‐SINGLE algorithm for which either sliding windows, fixed forgetting factors (corresponding to an EWMA model) or adaptive forgetting techniques are used. Second, we also look to quantify the ability of the rt‐SINGLE algorithm to accurately estimate time‐varying networks in real‐time. For this purpose, we consider the performance of the offline SINGLE algorithm as a benchmark. Naturally we expect the rt‐SINGLE algorithms to generally perform below its offline counterpart; however, the difference in performance will be indicative of how well the proposed methods work. We provide extensive details of the exact simulation settings as well as performance measures in Supporting Information C.
In Simulation 1, we study the quality of estimated covariance matrices over time. This simulation serves as a clear example of the advantages obtained via the use of adaptive filtering methods. In Simulations 2 and 3, we consider the overall performance of the proposed method by generating connectivity structures according to scale‐free and small‐world networks respectively. Finally, in Simulation 4, we look to quantify the computational cost of the proposed method as the number of nodes, p, increases; a crucial aspect to study given the objectives of this work.
Simulation 1 — Covariance Tracking
In this simulation, we look to assess how accurately we are able to track changes in covariance structure via the use of sliding windows, fixed (i.e., EWMA models) and adaptive forgetting factors.
Datasets were simulated as follows: each dataset consisted of five segments each of length 100 (i.e., overall duration of 500). The network structure within each segment was simulated according to either the Barabási and Albert [1999] preferential attachment model or using the Watts and Strogatz [1998] model. The use of each of these models was motivated by the fact that they are able to generate scale‐free and small‐world networks respectively; two classes of networks which are frequently encountered in the analysis of fMRI data [Bassett and Bullmore, 2006; Eguiluz et al., 2005; Sporns et al., 2004]. In this simulation, the estimated sample covariances from the proposed methods were compared to the results when using a symmetric Gaussian kernel, as in the offline SINGLE algorithm.
Figure 2 shows results when scale‐free (top) and small‐world (bottom) network structures are simulated over 500 independent simulations. We note that the quality of the estimated covariances drops in the proximity of a change‐point for all three real‐time algorithms. In the case of the offline SINGLE algorithm, this drop is symmetric due to the symmetric nature of the Gaussian kernel used. However, in the case of the real‐time algorithms the drop is highly asymmetric and occurs directly after the change‐point, as is to be expected. Due to the sudden change in covariance structure, these methods suffer immediately after abrupt changes in covariance structure, but are able to quickly recover. It is important to note the difference in behavior of each of the algorithms directly after a change‐point occurs. The use of fixed and adaptive forgetting factors results in rapid improvement compared to sliding windows. This is to be expected as sliding windows do not down‐weight past observations. Studying changes in covariance structure directly after a change occurs is of fundamental importance in neuroscientific research. In this context, the use of fixed and adaptive forgetting yields significant advantages. This is especially true for adaptive forgetting methods as highlighted in Figure 2.
Figure 2.
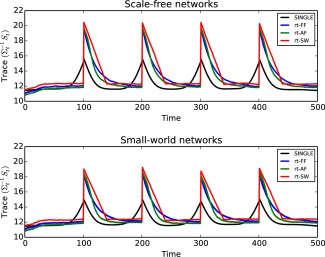
In this simulation, we study the capability of the proposed algorithm to accurately track changes to covariance structure over time. In order to quantify this, we consider the distance defined by the trace inner product, given in the supplementary material (Eq. (17)). We note that the symmetric Gaussian kernel used for the offline SINGLE algorithm outperforms the online algorithms as expected. However, when the covariance structure remains piece‐stationary for extended periods of time the online algorithms are able to outperform their offline counterparts. Moreover, the results demonstrate that adaptive filtering methods outperform both fixed forgetting factors as well as sliding windows.
Top: Covariance tracking results when underlying network structure is simulated according to the scale‐free preferential attachment model of [Barabási and Albert, 1999]. A change occurred every 100 observations.
Bottom: Covariance tracking results when the underlying network structure was simulated using small‐world random networks according to the model of Watts and Strogatz [1998]. [Color figure can be viewed at http://wileyonlinelibrary.com.]
For both scale‐free and small‐world networks, adaptive forgetting outperforms both fixed forgetting factors and sliding windows. These results, therefore, serve to clearly advocate the use of adaptive forgetting methods. Moreover, from Figure 2 we note that the covariance tracking capabilities of the proposed methods are not adversely affected by the choice of underlying network structure.
Simulation 2 — Scale‐Free Networks
In this simulation, we look to empirically quantify the capability of the proposed method to recover sparse covariance structure. As a benchmark, we compare the results of the rt‐SINGLE algorithm with the offline algorithm.
Datasets were simulated as described in Simulation 1, using the Barabási and Albert [1999] preferential attachment model. This generated scale‐free networks, implying that the degree distribution follows a power law. This implies the presence of a reduced number of hub nodes which have access to many other regions, while the remaining majority of nodes have a small number of edges [Eguiluz et al., 2005]. In this simulation, the entire dataset was simulated a priori. In the case of the rt‐SINGLE algorithms, one observation was provided at time, thereby treating the dataset as if it was a stream arriving in real‐time. The offline SINGLE algorithm was provided with the entire dataset and this was treated as an offline task.
In the left panel of Figure 3, we see the average scores for each of the real‐time algorithms as well as the offline algorithm over 500 simulations. We note that all algorithms experience a drop in F‐score in the proximity of change‐points. The offline SINGLE algorithm is based on a symmetric Gaussian kernel, as a result, we note that there it has a symmetric drop in performance in the vicinity of a change‐point before quickly recovering. Alternatively, the drop in performance of the rt‐SINGLE algorithms is asymmetric. This is due to the real‐time nature of these algorithms. In line with the results provided in Simulation 1, we note that when either the adaptive and fixed forgetting factor is used the performance of the algorithm after a change point increases rapidly. In contrast, when a sliding window is used a larger number of observations are required before an accurate estimate of the sample covariance can be obtained, resulting in poor recovery of the covariance structure.
Figure 3.
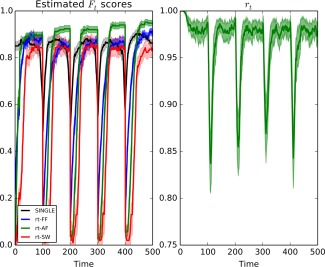
Left: Mean F scores for the offline SINGLE algorithm and the real‐time algorithms using either a sliding window (rt‐SW), a fixed forgetting factor (rt‐FF), or adaptive forgetting respectively (rt‐AF). Here, the underlying network structure was simulated using scale‐free random networks according to the preferential attachment model of Barabási and Albert [1999]. A change occurred every 100 time points. We note that all three algorithms experience a drop in performance in the vicinity of these change‐points, however in the case of the real‐time algorithms the drop is asymmetric. Moreover, we further note that when adaptive forgetting is used the real‐time algorithm is able to outperform its offline counterpart in sections where the data remains piece‐wise stationary for long periods of time.
Right: mean values for the estimated adaptive forgetting factor, , over time. We note there is a sudden drop directly after changes occurs allowing the algorithm to adequately discard irrelevant information. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Furthermore, we note that while the rt‐SINGLE algorithm performs worse than its offline counterpart directly after change‐points, it is able to quickly recover to the level of the offline SINGLE algorithm. Specifically, in the case where adaptive forgetting is used, the real‐time algorithm is able to outperform its offline counterpart in sections where the data remains piece‐wise stationary for long periods of time. This is because it is able to increase the value of the adaptive forgetting factor accordingly. This allows the algorithm to exploit a larger pool of relevant information compared to its offline counterpart. This is demonstrated on the right panel of Figure 3 where the mean value of the adaptive forgetting factor is plotted. We see there is a drop directly after changes occur; this allows the algorithm to quickly forget past information which is no longer relevant. We also note that the estimated value of the forgetting factor increases quickly after changes occur.
Simulation 3 — Small‐World Networks
While in Simulation 2 scale‐free networks were studied, it has been reported that brain networks follow a small‐world topology [Bassett and Bullmore, 2006]. Such networks are characterized by their high clustering coefficients which has been reported in both anatomical as well as functional brain networks [Sporns et al., 2004].
Datasets were simulated as described in Simulations 1 and 2, with the difference that individual networks were generated according to the Watts and Strogatz [1998] model. The Watts and Strogatz [1998] model works as follows: starting with a regular lattice, the model is parameterized by which quantifies the probability of randomly rewiring an edge. It follows that setting β = 0 results in a regular lattice, while setting results in an Erdős‐Rényi (i.e., completely random) network structure. Throughout this simulation we set as this yielded networks with sufficient variability but which still displayed the desired small‐world properties.
In the left panel of Figure 4, we see the average scores for each of the real‐time algorithms as well as the offline SINGLE algorithm over 500 simulations. Due to the increased complexity of small‐world networks, we note that the performance drops compared to scale‐free networks considered in Simulation 2. We further note that the rate at which the real‐time networks recover after a change‐point is reduced. As with Simulation 2, we note that the real‐time algorithms are able to reach the same level of performance as their offline counterpart if given sufficient time (i.e., if covariance structure is piecewise constant for sufficiently long periods of time). Moreover, in the case where adaptive forgetting is used we once again find that the performance of the real‐time algorithm exceeds that of the offline algorithm when the data remains piece‐wise stationary for a sufficiently long period of time. In the right panel of Figure 4, we see the estimated adaptive forgetting factor over each of the 500 simulations. Again, we see the drop in the value of the forgetting factor directly after change‐points; allowing past information to be efficiently discarded.
Figure 4.
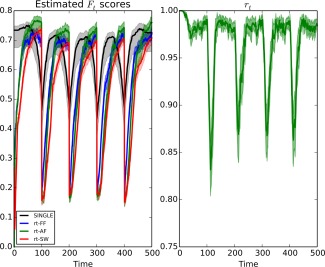
Left: Mean F scores for the offline SINGLE algorithm and the real‐time algorithms using either a sliding window (rt‐SW), fixed forgetting factor (rt‐FF), or adaptive forgetting respectively (rt‐AF). Here, the underlying network structure was simulated using small‐world random networks according to the model of Watts and Strogatz, Nature, 2012, 393, 440–442, reproduced by permission. A change occurred every 100 time points. We note that all three algorithms experience a drop in performance in the vicinity of these change‐points, however in the case of the rt‐SINGLE algorithms the drop is asymmetric. Moreover, we further note that when adaptive forgetting is used the real‐time algorithm is able to outperform its offline counterpart in sections where the data remains piece‐wise stationary for long periods of time.
Right: mean values for the estimated adaptive forgetting factor, , over time. We note there is a sudden drop directly after changes occurs allowing the algorithm to adequately discard irrelevant information. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Simulation 4 — Computational Cost
A fundamental aspect of real‐time algorithms is that they must be computationally efficient to be able to update parameter estimates in the limited time provided. The main computational cost of the rt‐SINGLE algorithm is related to the eigendecomposition of the update, which has a complexity of [Monti et al., 2014].
In this simulation, we look to empirically study the computational cost. In this manner, we are able to provide a rough guide as to the number of ROIs which can be used in a real‐time neurofeedback study while still reporting network estimates at every point in time. This was achieved by measuring the mean running time of each update iteration of the rt‐SINGLE algorithm for various numbers of ROIs, p.
Here, each dataset was simulated as in Simulation 2; that is the underlying correlation was randomly generated according to a scale‐free network. However, here we choose to only simulate three segments, each of length 50, resulting in a dataset consisting of 150 observations. For increasing values of p, the time taken to estimate a new precision matrix was calculated. Figure 5 shows the mean running time for the rt‐SINGLE algorithm where either a sliding window, a fixed forgetting factor (i.e., an EWMA model) or adaptive forgetting was used. We note that the difference in computational cost between each of the algorithms is virtually indistinguishable.
Figure 5.
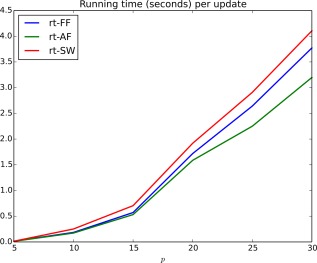
Mean running time (seconds) per update iteration of the rt‐SINGLE algorithm when either a sliding window (rt‐SW), a fixed forgetting factor (rt‐FF), or adaptive forgetting (rt‐AF) was used. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Finally, we note that when the number of nodes is below 20 it is possible to estimate functional connectivity networks in under 2 s, making the proposed method practically feasible in real‐time studies. This simulation was run on a computer with an Intel Core i5 CPU at 2.8 GHz.
APPLICATION
In this section, we present two applications of the proposed method. First, the proposed method is applied to motor‐task data taken from the HCP. Here, subjects were asked to perform a range of motor tasks. While this data was not acquired and analyzed in real‐time, it may be treated as such by only considering a single observation at a time. In this manner, we are able to compare the performance of the rt‐SINGLE algorithm to its offline counterpart using fMRI data as opposed to simulated examples, as was the case in Simulation Study section. The second application presented consists of a real‐time experiment where subjects were asked to perform a visuospatial search task. While the quality of the HCP data is arguable state‐of‐the‐art, the data generated in this experiment is of reduced quality. It, therefore, serves to demonstrate the capabilities of the rt‐SINGLE algorithm on a dataset that is more representative of typical fMRI data used in practice.
HCP Motor‐Task
Twenty of the 500 available task‐based fMRI datasets provided by the HCP were selected at random. Here, subjects were asked to perform a simple motor task adapted from those developed by Buckner et al. [2011] and Yeo et al. [2011]. This involved the presentation of visual cues asking subjects to either tap their fingers (left or right), squeeze their toes (left or right) or move their tongue. Each movement type was blocked, lasting 12 s, and was preceded by a 3 s visual cue. Each task was performed twice together with an additional three fixation blocks (each of length 15 s). This resulted in a total of 13 blocks per run.2
While this data is not intrinsically real‐time—in that the preprocessing was conducted after data acquisition—it is included as a proof‐of‐concept study. The data was preprocessed offline as the focus lies on the comparison between the real‐time and offline network estimation approaches rather than different preprocessing pipelines. Preprocessing involved regression of Friston's 24 motion parameters and high‐pass filtering using a cut‐off frequency of Hz.
Eleven bilateral cortical ROIs were defined based on the Desikan‐Killiany atlas [Desikan et al., 2006] covering occipital, parietal and temporal lobe (see Supporting Information Table 1 and Supporting Information Figure 1). These regions were selected based on the hypothesis that changes would occur in the sensory‐motor and higher‐level visual areas. The extracted time courses from these regions were subsequently used for the analysis. By treating the extracted time course data as if it was arriving in real‐time (i.e., considering one observation at a time), we can compare the results of the proposed real‐time method to offline algorithms while using the same underlying preprocessed data.
Results
Both the SINGLE as well as the rt‐SINGLE algorithms where applied to the motor‐task fMRI dataset. Our primary interest here is to report task‐driven changes in functional connectivity. In this way, we are able to examine if the rt‐SINGLE algorithm is capable of reporting the changes functional connectivity induced by the motor task.
The functional relationships that were modulated by the motor task were studied; this corresponds to studying the edges in the estimated networks which are significantly correlated with task onset. This was achieved by first estimating time‐varying functional connectivity networks using both the offline SINGLE algorithm as well as the proposed real‐time algorithm. In the case of the SINGLE algorithm, parameters where chosen as described in Monti et al. [2014]. This involved estimating the width of the Gaussian kernel via leave‐one‐out cross validation and estimating regularization parameters via minimizing AIC. In the case of the real‐time algorithm, adaptive forgetting was used with η = 0.005. The sparsity and temporal homogeneity parameters where set to the same values as the offline SINGLE algorithm as the focus here was to study differences induced by estimating networks in real‐time as opposed to differences resulting from different parameterizations.
To determine which edges where modulated by task a non‐parametric statistical test was performed. Formally, Spearman's rank correlation coefficient was estimated between the time‐varying estimated partial correlation values for each edge and the task‐evoked HRF function. It follows that edges which are modulated by the task will display strong correlations with the task HRF, thus allowing us to network of edges which are modulated by the motor task. Each estimated correlation coefficient was subsequently tested to determine if the correlation was statistically significant. The resulting P‐values (one for each edge) were then corrected for multiple comparisons via the Holm–Bonferroni method [Holm, 1979]. This allowed us to obtain an activation network, summarizing which edges are statistically activated by the motor task for each algorithm.
Figure 6 shows task activation networks for both the SINGLE and rt‐SINGLE algorithms. Edges are only present if they were reported as being significantly correlated with task‐evoked HRF function. Red edges indicated the strength of the edge increase during task while blue edges indicate the strength of the edge decrease during task (i.e., a negative correlation). Furthermore, edge thickness is indicative of the magnitude of the correlation. Figure 6 shows clear similarities across each of the algorithms, with 84% of edges reported by both the rt‐SINGLE and SINGLE algorithms. This would suggest that the rt‐SINGLE algorithm is accurately detecting task‐modulated changes in functional connectivity. In particular, we observe increased functional coupling between the motor‐sensory and visual regions in the occipital cortex as well as inferior and middle temporal heteromodal regions. These results are plausible with regard to the task that involved high‐level visual and heteromodal processing of the preceding visual cues and the execution of the actual movement and have been previously reported [Hein and Knight, 2008; Zilverstand et al., 2014].
Figure 6.
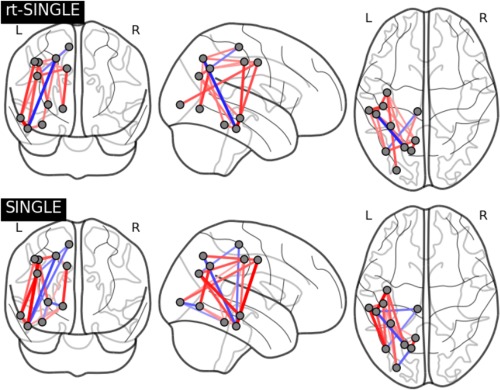
Task activation networks for rt‐SINGLE (top) and SINGLE (bottom) algorithms, respectively. Present edges had statistically significant correlations with task HRF after correction for multiple comparisons. Red edges indicate edge strength increased during task while blue edges indicate edge strength decreased during task. Eleven bilateral regions where used as described in Table 1. In order to facilitate interpretation of the plot, only the right‐hemispheric coordinates are shown here. We note there is consistent activation pattern across both algorithms, particularly across nodes nodes corresponding to the motorsensory areas. Associated summary graph statistics of the task positive and task negative networks estimated with rt‐SINGLE and SINGLE are provided in Supporting Information Table 2. [Color figure can be viewed at http://wileyonlinelibrary.com.]
While Figure 6 serves to visually demonstrate that the rt‐SINGLE algorithm is accurately detecting task‐modulated changes in connectivity, we also studied graph theoretic properties to quantify if there are significant differences in the graph structure of networks estiamted using offline SINGLE and rt‐SINGLE algorithms. While there are many candidate graph statistics which can be studied, in this work we look to study the three key properties; the mean degree centrality across nodes,3 the mean betweenness centrality over edges in the network4 and the transitivity of the network.5 Furthermore, the changes in network statistics where studied in the context of task positive and task negative modulation, thereby allowing us to study in detail if significant differences occurred in the estimated network structure. As such, graph statistics were calculated for the network of positively and negatively task‐modulated edges respectively (that is the networks corresponding to the red and blue edges in Fig. 6, respectively). The results of this supporting analysis are provided in Supporting Information Table 2. We note we found no significant differences between each of the two algorithms in each of the selected graph statistics. These results serve as evidence that the proposed method can perform comparably with offline methods despite facing the additional challenge of estimating networks “on‐the‐fly.”
Moreover, in a rt‐fMRI study it is also crucial to be able to accurately estimate functional connectivity networks for individual subjects. While the true underlying functional connectivity networks are unknown (and may vary for each subject), we are able to quantify how closely the networks estimated in real‐time recreate the results of an offline analysis. As a result, the correlation was studied between the estimated edges using both the rt‐SINGLE and the offline SINGLE algorithms. This was performed on a subject‐by‐subject basis. For each edge, the correlation between the estimated edge values using each of the two algorithms was quantified using Spearman's rank correlation coefficient and the corresponding P‐values were corrected for multiple comparisons. Figure 7 shows the subject‐specific networks containing only edges that were significantly correlated across both algorithms. As before, red edges indicate a positive correlation with task while blue edges are indicative of negative correlations and the thickness of the edges is proportional to the strength of the correlation. We note the resulting networks are dense across all subjects and the vast majority of edges indicate positive correlations. In particular, an average of 74% of edges were positively correlated across all subjects.6
Figure 7.
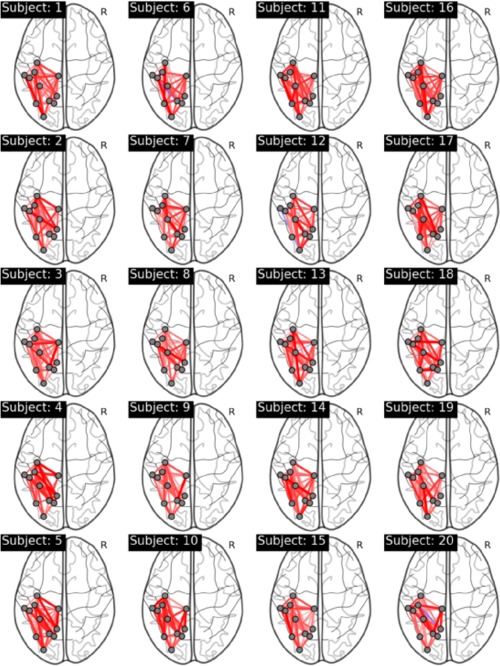
Subject specific networks visualizing edges that were significantly correlated across both the rt‐SINGLE algorithm and its offline counterpart. Red edges indicate positive correlations while blue edges indicate negative correlations. We note that networks are dense across all subjects, indicating that the rt‐SINGLE algorithm is able to accurately recover network structures similar to an offline study. Associated summary graph statistics of the task positive and task negative networks across all subjects are provided in Supporting Information Table 3. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Table 1.
Regions and MNI coordinates used in the study of HCP data described in HCP Motor‐Task section
| Name | Right hem. | Left hem. | ||||
|---|---|---|---|---|---|---|
| Lateral occipital | 31 | −84 | 1 | −29 | −87 | 1 |
| Inferior parietal | 43 | −62 | 30 | −39 | −68 | 30 |
| Superior parietal | 22 | −62 | 48 | −21 | −64 | 47 |
| Precuneus | 11 | −56 | 37 | −10 | −57 | 37 |
| Fusiform | 34 | −39 | −20 | −34 | −43 | −19 |
| Lingual | 15 | −66 | −3 | −14 | −67 | −3 |
| Inferior temporal | 49 | −26 | −25 | −49 | −31 | −23 |
| Middle temporal | 57 | −22 | −14 | −56 | −27 | −12 |
| Precentral | 39 | −8 | 43 | −38 | −9 | 43 |
| Postcentral | 42 | −21 | 44 | −42 | −23 | 44 |
| Paracentral | 9 | −26 | 58 | −8 | −28 | 59 |
Here, the MNI coordinates correspond to the center of gravity of each of the respective regions.
As noted previously, it is also important to study graph theoretic properties of the estimated networks to quantitatively study wethere there are signficant differences in the network structure across subjects. As a result, we computed the three aforementioned graph statistics over the subject‐specific estimated networks shown in Figure 7. Furthermore, as discussed previously, the graph statistics were considered for the task positive and task negative networks (that is the networks corresponding to the red and blue edges in Fig. 7 respectively). In this manner, we were able to study if significant differences occured across subjects in a detailed fashion. The results, provided in Supporting Information Table 3, show that the estimated graph statistics are stable and consistent across the cohort of subjects. This serves as an indication that graph statistics such as the betweenness centrality are robust across a cohort of subjects and therefore suitable candidates for neurofeedback applications.
Real‐Time Visuospatial Attention Task
While the HCP dataset introduced in HCP Motor‐Task section serves to demonstrate the reliability of the real‐time network estimates, our proposed method was also tested using data that was processed and studied alongside data acquisition. The data used here corresponds to fMRI data acquired over 20 subjects during the visuospatial attention task described in Braga et al. [2013]. Briefly, the task corresponded to a visual attention task explicitly designed to engage subjects with continuous top‐down visual monitoring of stimuli. Subjects where shown complex and naturalistic moving scenes and where required to detect a 1 s change in color of the target stimuli (from red to green) [Braga et al., 2013]. The target consisted of a red rectangle which appeared in two possible locations of the screen (top‐left or bottom‐right). The task, therefore, consisted of a pre‐target phase where subjects were attentively viewing the color video footage as well as a post‐target phase, where subjects had reported the target change and were no longer required to attentively watch the video. A total of twenty trials were performed for each subject, however in selected trials no target stimuli was presented. Note that the stimuli that subjects perceived in the two conditions (pre‐ and post‐target) were exactly identical; the only difference consisted in the attentional state of the subject.
In terms of data quality, the HCP dataset used in HCP Motor‐Task section was acquired using state‐of‐the‐art parallel imaging which resulted in higher temporal resolution (TR = 0.72 s) and increased signal‐to‐noise ratio [Elam and Van Essen, 2014]. In contrast, the data used here is of far lower quality; having a TR of 3 s. Furthermore, unlike the HCP dataset, preprocessing was not performed offline here, posing further limitations on the quality of the data.
While the entire dataset was collected and studied in Braga et al. [2013], in this work it was treated in a real‐time fashion. The rt‐fMRI pipeline used is described in Simulated real‐time fMRI pipeline section below. Given that we are trying to capture differences in hidden attentional states (in contrast to overt motor movements as in the case of the HCP data), this data corresponds to a far more complicated cognitive task. This, therefore, serves to validate the capabilities of the proposed method with a dataset that is representative of data typically used in rt‐fMRI studies.
As we look to corroborate previous results relating to the top‐down visuospatial attention networks, we created spheres of 10 mm radius positioned at the center of gravity of 11 activation clusters derived from a spatially constrained independent component analysis (ICA) on the data (as reported in Braga et al. [2013]) in addition to three subregions of the dorsal attention network (DAN) obtained from Capotosto et al. [2009] and Dosenbach et al. [2007] (also reported in Braga et al. [2013]). The regions, summarized in Supporting Information Table 4, showed significant differences between pre‐ and post‐target phase in the original study and where, therefore, used to study the reliability of the proposed rt‐SINGLE algorithm.
Simulated real‐time fMRI pipeline
Whole‐brain coverage images were acquired by a Philips Intera 3.0 T MRI system with an 8‐element phased array head coil and sensitivity encoding using an echoplanar imaging (EPI) sequence (T2*: FOV = 220 × 143 × 190 mm, time repetition (TR)/time echo (TE): 3,000/45 ms, 44 axial slices with slice thickness of 3.5 mm). A total of 335 EPI images were acquired for each subject. In addition, a high‐resolution (1 mm × 1 mm × 1 mm) T1‐weighted whole‐brain structural image (reference anatomical image, RAI) was obtained for each participant. Prior to the simulated online preprocessing of the data, the first EPI volume (reference functional image, RFI) was used for spatial co‐registration. The first step comprised the brain extraction of the RAI and RFI using BET [Smith, 2002], followed by an affine co‐registration of the RFI to RAI and subsequent nonlinear registration to a standard brain atlas (MNI) using FNIRT [Andersson et al., 2007]. The resulting transformation matrix was used to register the 14 ROIs (as described in Real‐Time Visuospatial Attention Task section and Supporting Information Table 4) from MNI to the functional space of the respective subject. For simulated online processing, incoming raw EPI images were motion corrected in simulated real‐time using MCFLIRT [Jenkinson et al., 2002] with the previously obtained RFI acting as reference. In addition, images were spatially smoothed using a 5 mm FWHM Gaussian kernel. ROI means for each TR were simultaneously extracted using a general linear model approach and written into a text file that was accessed by the rt‐SINGLE algorithm. Based on these time courses, rt‐SINGLE estimated time‐varying functional connectivity networks for each TR. In total, the full processing of the data in simulated real‐time took under 1 s per observation, leaving considerable time for the optimization required of the rt‐SINGLE algorithm.
Results
The rt‐SINGLE algorithm was applied to fMRI data corresponding to the visuospatial task. As in HCP Motor‐Task section, our primary interest here was to demonstrate that the proposed real‐time algorithm was able to accurately report changes in functional connectivity.
The real‐time pipeline described in Simulated real‐time fMRI pipeline section was used to estimate time‐varying functional connectivity networks for each subject independently. A burn‐in period of 10 observations was used. This allowed the sparsity and temporal homogeneity parameters to be selected by minimizing AIC over this burn‐in period. Finally, adaptive filtering was used to estimate subject covariance matrices with tuning parameter η = 0.005.
To report the functional networks (i.e., edges) modulated by the task, we report the edges which are significantly correlated with task HRF function. For each edge, the correlation between the mean estimated partial correlation across subjects and the HRF was computed using Spearman's rank correlation coefficient. As with the HCP task, resulting P‐values where corrected for multiple comparisons, resulting in a network containing only statistically significant edges.
Figure 8 shows the task activation network as estimated by the rt‐SINGLE algorithm. Edges are only present if they were reported as being statistically correlated with the task HRF function. The edge color is indicative of the behavior of a particular edge: red edges are upregulated during the pre‐attention phase (attentive visual search) while blue edges are upregulated during the post‐attention phase (passive viewing).
Figure 8.
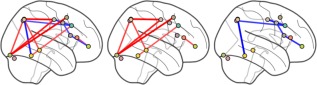
Task activation networks for rt‐SINGLE algorithm shown on the left panel. Present edges had statistically significant correlations with task HRF after correction for multiple comparisons. Red edges were upregulated during attentive visual searching while blue edges were upregulated during the passive viewing phase. For clarity, edges corresponding to attentive visual search and passive viewing are plotted separately in the middle and right panels. Associated summary graph statistics of the networks associated with attentive visual search as well as passive viewing are provided in Supporting Information Table 5. [Color figure can be viewed at http://wileyonlinelibrary.com.]
We note there is stronger coupling for the visual top‐down attention condition between the right superior parietal lobe (SPL) and the right frontal eye fields (FEF), the right occipital fusiform as well as the right middle temporal gyrus. In addition, for the same condition we observe stronger coupling between the right occipital fusiform and the right FEF as well as the left SPL. Furthermore, functional connectivity between the right inferior temporal gyrus and right middle frontal gyrus is increased for the top‐down attention. These results are in line with a previous, non real‐time analysis of this data [Braga et al., 2013], as well as accounts of visual top‐down attention regulation in the literature. Typically, during visual top‐down attention the visual cortices become functionally connected with higher‐order frontoparietal regions the SPL and FEF, making up what is known as the DAN [Corbetta and Shulman, 2002; Corbetta et al., 2008].
Finally, we also study functional connectivity networks estimated on a subject‐by‐subject basis. As in HCP Motor‐Task section, we study some of the graph theoretic properties obtained across subjects to verify if the estimated networks are robust across subjects. Subject‐specific functional connectivity networks were estimated as described above and three measures of graph structure where collected; the mean degree centrality across nodes, the mean betweenness centrality across edges and the transitivity (i.e., clustering coefficient) of the network. Moreover, as discussed in HCP Motor‐Task section, the graph statistics were estimated for the network of upregulated edges associated with attentive visual search (red edges in Fig. 8) as well as the network of upregulated edges associated with passive viewing (blue edges in Fig. 8). The results, provided in Supporting Information Table 5, indicate that networks estimated across subjects show robust and reproducible properties for both the attentive visual search and the passive viewing network. These results are reassuring in the context of real‐time fMRI neurofeedback as they validate the potential use of graph statistics.
DISCUSSION
In this work, we introduce a novel methodology with which to estimate dynamic functional connectivity networks in real‐time. The contributions of the proposed method can be summarized as follows. First, we propose the use of adaptive forgetting methods to obtain highly adaptive estimates of the sample covariance over time. Such methods designate that choice of the forgetting factor to the data, making them highly adaptive as well as flexible. The latter point is of particular importance in the rt‐fMRI setting; since changes in functional connectivity may occur abruptly and at varying intervals, the assumptions behind the use of fixed forgetting factors or sliding windows do not necessarily hold true. Second, by extending the recently proposed SINGLE algorithm we are able to accurately estimate functional connectivity networks based on precision matrices in real‐time.
The proposed method enforces constraints on both the sparsity as well as the temporal homogeneity of estimated functional connectivity networks. The former is required to ensure the estimation problem remains well‐posed when the number of relevant observations drops, as is bound to occur when adaptive forgetting is used. Conversely, the temporal homogeneity constraint ensures changes in functional connectivity are only reported when heavily substantiated by evidence in the data. As we demonstrate through a series of simulation studies, the rt‐SINGLE algorithm is able to both obtain accurate estimates of functional connectivity networks at each point in time as well as accurately describe the evolution of networks over time.
The rt‐SINGLE algorithm is closely related to sliding window methods which have been used extensively in the real‐time setting [Esposito et al., 2003; Gembris et al., 2000; Ruiz et al., 2014; Zilverstand et al., 2014]. Extensions of sliding window methods, such as EWMA models, have been successfully applied to offline fMRI studies [Lindquist et al., 2007] and have been shown to be better suited to estimating dynamic functional connectivity [Lindquist et al., 2014]. In this work we considered both sliding windows and EWMA models alongside adaptive forgetting. We presented an extensive simulation study comparing these three methods which demonstrates the advantages of adaptive filtering methods. However, the proposed method is flexible and can be implemented using either sliding windows, fixed forgetting factors (corresponding to an EWMA model) or adaptive forgetting.
The proposed method requires the input of three parameters. The first of these parameters, stepsize η, governs the rate at which an adaptive forgetting factor, , varies and can be interpreted as the stepsize in a stochastic gradient descent scheme [Bottou, 2004]. The final two parameters enforce sparsity and temporal homogeneity respectively. These parameters remain fixed throughout in a similar manner to the fixed forgetting factor and two heuristic approaches are proposed to tune these parameters. A future improvement for the proposed algorithm would involve adaptive regularization penalties. However, such approaches are computationally and theoretically challenging due to the non‐differentiable nature of the penalty terms.
Two applications of the proposed method were provided. The first involved motor‐task data from the HCP. The results demonstrate that the rt‐SINGLE algorithm was able to accurately detect functional networks which are modulated by motor task. The second application corresponds to a more complex visuospatial attention task. While the quality of the HCP data used is arguably state‐of‐the‐art, this dataset was used to demonstrate the capabilities of the rt‐SINGLE algorithm using fMRI data as opposed to simulated examples. In contrast, the quality of the second dataset studied is of similar quality than would be expected in a typical rt‐fMRI study; as it corresponds to a low temporal resolution (3 s) and a complex cognitive task. Both datasets were analyzed in real‐time and provide compelling evidence that the proposed method is able to accurately track functional connectivity “on‐the‐fly.” Moreover, throughout these two applications networks were estimated every TR. However, depending on the nature of the experiment, it would be possible to only obtain an updated estimate of the functional connectivity networks every several TRs.
It is well known in the neuroimaging field that the choice of pre‐processing strategy has a significant effect on connectivity estimates [Gavrilescu et al., 2008; Weissenbacher et al., 2009].This aspect receives even more importance for dynamic FC methods as time‐varying connectivity estimates are based on relatively few TRs [Hutchison et al., 2013]. Therefore, when conducting dynamic FC analysis, it is suggested to perform typical pre‐processing steps applied to resting‐state fMRI data (such as motion correction, spatial filtering, nuisance regression and high‐pass filtering) in addition to recording respiration and cardiac events for further de‐noising of the data [Hutchison et al., 2013]. However, these recommendations have been worked out for dynamic FC analysis on resting‐state data. When looking at task‐induced changes in FC, standard pre‐processing strategies have predominantly been used in the field [Monti et al., 2014] and high reproducibility of results has been reported when comparing minimally pre‐processed with highly pre‐processed ROI time‐courses [Allen et al., 2014]. So, in case equally distributed noise can be expected for blocks of task and blocks of no task performance, dynamic FC methods will be able to capture the task‐induced difference in FC. As reported above, the HCP data can be considered as an extensively and (offline) pre‐processed dataset while the other dataset more closely matches the description of a minimally pre‐processed dataset. For both datasets, we obtained results that are highly consistent with previous findings. Importantly although, more exhaustive pre‐processing could hypothetically be performed in real‐time (such as nuisance regression, de‐spiking etc.), thus not precluding the use of rt‐SINGLE for resting‐state data.
Besides the impact of different pre‐processing strategies on time‐varying FC results, the ad hoc ROI selection is crucial for the success of the method and interpretation of the findings. Contrary to offline analyses, in which the ROI selection itself can be an explorative process (although this might not be considered as conservative scientific approach), the real‐time nature of our proposed method requires an adequate consideration of the most suitable ROIs a priori to the experiment. For our work presented here, we have selected the respective nodes in a strictly hypothesis‐driven manner. While for the motor task, we have included nodes within sensory‐motor and higher‐level visual areas, for the visuospatial attention task we based on our node selection on activation clusters derived from a previous analysis of the same dataset that consisted of core regions of the top‐down visuospatial attention network. We, therefore, strongly hypothesized these nodes to be modulated by the respective tasks. Besides such a hypothesis‐driven ROI‐based approach, another popular and more data‐driven strategy is to parcellate the brain into large‐scale functional brain network [Smith et al., 2009] and compute time‐varying connectivity estimates based on the extracted network time‐courses [Allen et al., 2014; Calhoun et al., 2014]. Although the most common approach is to measure dynamic FC by looking at changes in correlation over time while assuming fixed ROIs or networks [Calhoun et al., 2014], recent approaches also take the spatio‐temporal nature of fMRI data into account by studying how the spatial patterns of regions/network changes over time [Karahanoglu and Van de Ville, 2015; Ma et al., 2011; Scott et al., 2015]. However to date, none of these approached would be suitable for a real‐time application.
In conclusion, the rt‐SINGLE algorithm provides a novel method for estimating functional connectivity networks in real‐time. We present two applications demonstrating that the rt‐SINGLE algorithm is capable of reporting changes in motor execution as well as internal attentional state of subjects. In future, the proposed method could be incorporated into rt‐fMRI studies, potentially providing neurofeedback based on functional connectivity. De Bettencourt et al. [2015] convincingly demonstrated that closed‐loop neurofeedback can be used to improve sustained attention abilities and reduce the frequency of lapses in attention. The authors used multivariate pattern analysis and found that behavioral improvement was the largest when feedback carried information from a frontoparietal attention network. Especially with regard to our second example, we demonstrate that rt‐SINGLE is able to capture moment‐to‐moment fluctuations in the attentional state of subjects and could potentially be used to boost brain state decoding accuracy by providing additional information relating to functional connectivity. Finally, there is great potential to integrate this work with the recently proposed Automatic Neuroscientist framework of Lorenz et al. [2016a]. Lorenz et al. [2016a] combined real‐time fMRI with machine learning techniques to optimize experimental conditions to maximize a given target brain state [Lorenz et al., 2015, 2016a]. While the target brain state in their proof‐of‐principle study was simply based on BOLD differences, our proposed method can be utilized to extend the Automatic Neuroscientist to target entire functional connectivity networks. This could be of paramount importance for the framework to be pulled through the translational pathway as various neurological and psychiatric disorders are characterized by disruption of functional networks such as attention deficit disorder [Stins et al., 2005], traumatic brain injury [Whyte et al., 1995], or bipolar disorder [Clark et al., 2002].
Supporting information
Supporting Information
ACKNOWLEDGMENT
Data were provided (in part) by the Human Connectome Project, WU‐Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657).
Figures [6] to [8] were produced using the nilearn library [Abraham et al., 2014].
Footnotes
We note that Eqs. (4) and (5) are equivalent to estimating the sample covariance in the more intuitive manner ; however, we choose to follow this parameterization in order to simplify future discussion.
For further details, please see http://www.humanconnectome.org/documentation/Q1/task-fMRI-protocol-details.html
The degree centrality of a node is defined as the sum of its weighted edges.
Betweenness centrality of an edge is a measure of the importance of the edge. Briefly, it measures the proportion of shortest paths between any two nodes which include the edge.
The transitivity of a network is a measure of the clustering of the network which studies how likely it is that nodes in the network will cluster together.
Under the null hypothesis that the edges of dynamic networks estimated using the rt‐SINGLE and SINGLE algorithms respectively are uncorrelated, we would expect zero edges to be present (i.e., an empty graph) with 95% probability. This is because by implementing the Holm–Bonferroni method we have controlled the family wise error rate at the level.
REFERENCES
- Abraham A, Pedregosa F, Eickenberg M, Gervais P, Mueller A, Kossaifi J, Gramfort A, Thirion B, Varoquaux G (2014): Machine learning for neuroimaging with scikit‐learn. Front Neuroinform 8:14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen E, Damaraju E, Plis S, Erhardt E, Eichele T, Calhoun V (2014): Tracking whole‐brain connectivity dynamics in the resting state. Cereb Cortex 24:663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anagnostopoulos C, Tasoulis D, Adams N, Pavlidis N, Hand D (2012): Online linear and quadratic discriminant analysis with adaptive forgetting for streaming classification. Stat Anal Data Min 5:139–166. [Google Scholar]
- Andersson J, Jenkinson M, Smith S (2007): Non‐linear registration, aka spatial normalisation FMRIB technical report. FMRIB Analysis Group of the University of Oxford. [Google Scholar]
- Ball G, Aljabar P, Zebari S, Tusor N, Arichi T, Merchant N, Robinson EC, Ogundipe E, Rueckert D, Edwards AD, Counsell SJ (2014): Rich‐club organization of the newborn human brain. Proc Natl Acad Sci USA 111:7456–7461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási A, Albert R (1999): Emergence of scaling in random networks. Science 286:509–512. [DOI] [PubMed] [Google Scholar]
- Bassett D, Bullmore E (2006): Small‐world brain networks. Neuroscientist 12:512–523. [DOI] [PubMed] [Google Scholar]
- Bassett D, Wymbs N, Porter M, Mucha P, Carlson J, Grafton S (2011): Dynamic reconfiguration of human brain networks during learning. Proc Natl Acad Sci USA 108:7641–7646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertsekas DP (1982): Constrained Optimisation and Lagrange Multiplier Methods. Academic Press. [Google Scholar]
- Bettencourt MD, Cohen JD, Lee RF, Norman KA, Turk‐Browne NB (2015): Closed‐loop training of attention with real‐time brain imaging. Nat Neurosci 18:470–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Zerrin V, Haughton Y, Hyde J (1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34:537–541. [DOI] [PubMed] [Google Scholar]
- Bonnelle V Leech R, Kinnunen K, Ham T, Beckmann C, De Boissezon X, Greenwood R, Sharp D (2011): Default mode network connectivity predicts sustained attention deficits after traumatic brain injury. J Neurosci 31:13442–13451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottou L (2004): Stochastic learning In: Advanced lectures on machine learning. Springer; pp. 146–168. [Google Scholar]
- Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2010): Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3:1–122. [Google Scholar]
- Braga R, Wilson L, Sharp D, Wise R, Leech R (2013): Separable networks for top‐down attention to auditory non‐spatial and visuospatial modalities. Neuroimage 74:77–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler S, Menon V (2010): Large‐scale brain networks in cognition: Emerging methods and principles. Trends Cogn Sci 14:277–290. [DOI] [PubMed] [Google Scholar]
- Buckner R, Sepulcre J, Talukdar T, Krienen F, Liu H, Hedden T, Andrews‐Hanna J, Sperling R, Johnson K (2009): Cortical hubs revealed by intrinsic functional connectivity: Mapping, assessment of stability, and relation to Alzheimer's disease. J Neurosci 29:1860–1873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner R, Krienen F, Castellanos A, Diaz J, Yeo BT (2011): The organization of the human cerebellum estimated by intrinsic functional connectivity. J Neurophysiol 106:2322–2345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nature 10:186–198. [DOI] [PubMed] [Google Scholar]
- Calhoun V, Miller R, Pearlson G, Adalı T (2014): The chronnectome: Time‐varying connectivity networks as the next frontier in fMRI data discovery. Neuron 84:262–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capotosto P, Babiloni C, Romani G, Corbetta M (2009): Frontoparietal cortex controls spatial attention through modulation of anticipatory alpha rhythms. J Neurosci 29:5863–5872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan M, Park D, Savalia N, Petersen S, Wig G (2014): Decreased segregation of brain systems across the healthy adult lifespan. Proc Natl Acad Sci USA 111:E4997–E5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover G (2010): Time–frequency dynamics of resting‐state brain connectivity measured with fMRI. Neuroimage 50:81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark L, Iversen SD, Goodwin GM (2002): Sustained attention deficit in bipolar disorder. Br J Psychiatry 180:313–319. [DOI] [PubMed] [Google Scholar]
- Corbetta M, Shulman G (2002): Control of goal‐directed and stimulus‐driven attention in the brain. Nat Rev Neurosci 3:201–215. [DOI] [PubMed] [Google Scholar]
- Corbetta M, Patel G, Shulman G (2008): The reorienting system of the human brain: From environment to theory of mind. Neuron 58:306–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox R, Jesmanowicz A, Hyde J (1995): Real‐time functional magnetic resonance imaging. Magn Reson Med 33:230–236. [DOI] [PubMed] [Google Scholar]
- Cribben I, Haraldsdottir R, Atlas YL, Wager TD, Lindquist MA (2012): Dynamic Connectivity Regression: Determining state‐related changes in brain connectivity. NeuroImage 61:907–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison E, Schlesinger K, Bassett D, Lynall M, Miller M, Grafton S, Carlson J (2015): Brain network adaptability across task states. PLoS Comput Biol 11:e1004029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- deCharms C (2008): Applications of real‐time fMRI. Nat Rev Neurosci 9:720–729. [DOI] [PubMed] [Google Scholar]
- Desikan R, Ségonne F, Fischl B, Quinn B, Dickerson B, Blacker D, Buckner R, Dale A, Maguire R, Hyman B (2006): An automated labeling system for subdividing the human cerebral cortex on mri scans into gyral based regions of interest. Neuroimage 31:968–980. [DOI] [PubMed] [Google Scholar]
- Dosenbach N, Fair D, Miezin F, Cohen A, Wenger K, Dosenbach R, Fox M, Snyder A, Vincent J, Raichle M (2007): Distinct brain networks for adaptive and stable task control in humans. Proc Natl Acad Sci USA 104:11073–11078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eguiluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV (2005): Scale‐free brain functional networks. Phys Rev Lett 94:018102. [DOI] [PubMed] [Google Scholar]
- Eklund A, Ohlsson H, Andersson M, Rydell J, Ynnerman A, Knutsson H (2009): Using real‐time fMRI to control a dynamical system by brain activity classification In: Medical Image Computing and Computer‐Assisted Intervention–MICCAI 2009. Springer; pp 1000–1008. [DOI] [PubMed] [Google Scholar]
- Elam J, Van Essen D (2014): Human Connectome Project In: Encyclopedia of Computational Neuroscience. Springer; pp 1–4. [Google Scholar]
- Elton A, Gao W (2014): Divergent task‐dependent functional connectivity of executive control and salience networks. Cortex 51:56–66. [DOI] [PubMed] [Google Scholar]
- Esposito F, Seifritz E, Formisano E, Morrone R, Scarabino T, Tedeschi G, Cirillo S, Goebel R, Di Salle F (2003): Real‐time independent component analysis of fMRI time‐series. Neuroimage 20:2209–2224. [DOI] [PubMed] [Google Scholar]
- Fornito A, Harrison B, Zalesky A, Simons J (2012): Competitive and cooperative dynamics of large‐scale brain functional networks supporting recollection. Proc Natl Acad Sci USA 109:12788–12793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K (1994): Functional and effective connectivity in neuroimaging: A synthesis. Hum Brain Mapp 2:56–78. [Google Scholar]
- Gavrilescu M, Stuart G, Rossell S, Henshall K, McKay C, Sergejew A, Copolov D, Egan G (2008): Functional connectivity estimation in fMRI data: Influence of preprocessing and time course selection. Hum Brain Mapp 1040–1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gembris D, Taylor J, Schor S, Frings W, Suter D, Posse S (2000): Functional magnetic resonance imaging in real time (fire): Sliding‐window correlation analysis and reference‐vector optimization. Magn Reson Med 43:259–268. [DOI] [PubMed] [Google Scholar]
- Haykin S (2008): Adaptive Filter Theory. Pearson. [Google Scholar]
- Hein G, Knight R (2008): Superior temporal sulcus—it's my area: Or is it? J Cogn Neurosci 20:2125–2136. [DOI] [PubMed] [Google Scholar]
- Holm S (1979): A simple sequentially rejective multiple test procedure. Scand J Stat 6:65–70. [Google Scholar]
- Hunter JS (1986): The exponentially weighted moving average. J Qual Technol 18:203–210. [Google Scholar]
- Hutchison M, Womelsdorf T, Allen E, Bandettini P, Calhoun V, Corbetta M, Della Penna S, Duyn J, Glover G, Gonzalez‐Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C (2013): Dynamic functional connectivity: Promise, issues, and interpretations. Neuroimage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S (2002): Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17:825–841. [DOI] [PubMed] [Google Scholar]
- Karahanoglu F, Van de Ville D (2015): Transient brain activity disentangles fMRI resting‐state dynamics in terms of spatially and temporally overlapping networks. Nat Commun 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koush Y, Rosa M, Robineau F, Heinen K, Rieger S, Weiskopf N, Vuilleumier P, Van De Ville D, Scharnowski F (2013): Connectivity‐based neurofeedback: Dynamic causal modeling for real‐time fMRI. NeuroImage 81:422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaConte S (2011): Decoding fMRI brain states in real‐time. Neuroimage 56:440–454. [DOI] [PubMed] [Google Scholar]
- LaConte S, Peltier S, Hu X (2007): Real‐time fMRI using brain‐state classification. Hum Brain Mapp 28:1033–1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauritzen S (1996): Graphical Models. Oxford University Press. [Google Scholar]
- Leonardi N, Richiardi J, Gschwind M, Simioni S, Annoni J‐M, Schluep M, Vuilleumier P, Van De Ville D (2013): Principal components of functional connectivity: A new approach to study dynamic brain connectivity during rest. NeuroImage 83:937–950. [DOI] [PubMed] [Google Scholar]
- Liew SL, Rana M, Cornelsen S, de Barros Filho MF, Birbaumer N, Sitaram R, Cohen LG, Soekadar SR (2015): Improving motor corticothalamic communication after stroke using real‐time fMRI connectivity‐based neurofeedback. Neurorehabil Neural Repair 30:671–675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindquist M, Waugh C, Wager T (2007): Modeling state‐related changes in fMRI activity using change‐point theory. NeuroImage 5:1125–1141. [DOI] [PubMed] [Google Scholar]
- Lindquist M, Xu Y, Nebel M, Caffo B (2014): Evaluating dynamic bivariate correlations in resting‐state fMRI: A comparison study and a new approach. NeuroImage 101:531–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz R, Monti RP, Violante IR, Faisal AA, Anagnostopoulos C, Leech R, Montana G (2015): Stopping criteria for boosting automatic experimental design using real‐time fMRI with Bayesian optimization. arXiv preprint arXiv. NIPS workshop on Machine Learning in Neuroimaging, 2015, 1511. [Google Scholar]
- Lorenz R, Monti RP, Violante IR, Anagnostopoulos C, Faisal A, Montana G, Leech R (2016a): The automatic neuroscientist: A framework for optimizing experimental design with closed‐loop real‐time fMRI. NeuroImage 129:320–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz R, Monti RP, Hampshire A, Koush Y, Anagnostopoulos C, Faisal AA, Sharp D, Montana G, Leech R, Violante IR (2016b): Towards tailoring non‐invasive brain stimulation using real‐time fMRI and Bayesian optimization. arXiv preprint arXiv 1605. [Google Scholar]
- Ma S, Correa NM, Li XL, Eichele T, Calhoun VD, Adali T (2011): Automatic identification of functional clusters in fMRI data using spatial dependence. IEEE Trans Biomed Eng 58:3406–3417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrelec G, Kim J, Doyon J, Horwitz B (2009): Large‐scale neural model validation of partial correlation analysis for effective connectivity investigation in functional MRI. Hum Brain Mapp 30:941–950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michel V, Gramfort A, Varoquaux G, Eger E, Thirion B (2011): Total variation regularization for fMRI‐based prediction of behavior. IEEE Trans Med Imaging 30:1328–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti RP, Hellyer P, Sharp D, Leech R, Anagnostopoulos C, Montana G (2014): Estimating time‐varying brain connectivity networks from functional MRI time series. NeuroImage 103:427–443. [DOI] [PubMed] [Google Scholar]
- Monti RP, Lorenz R, Hellyer P, Leech R, Anagnostopoulos C, Montana G (2015): Graph embeddings of dynamic functional connectivity reveal discriminative patterns of task engagement in hcp data. In IEEE 2015 International Workshop on Pattern Recognition in Neuroimaging (PRNI), Stanford, CA.
- Monti RP, Lorenz R, Leech R, Anagnostopoulos C, Montana G (2016): Streaming regularization parameter selection via stochastic gradient descent. arXiv. [Google Scholar]
- Nocedal J, Wright SJ (2006): Numerical Optimisation. Springer. [Google Scholar]
- Park H‐J, Friston K (2013): Structural and functional brain networks: From connections to cognition. Science 342:1238411. [DOI] [PubMed] [Google Scholar]
- Petersen K, Pedersen M (2008): The Matrix Cookbook. Technical University of Denmark; pp 7–15. [Google Scholar]
- Pinter D, Beckmann C, Koini M, Pirker E, Filippini N, Pichler A, Fuchs S, Fazekas F, Enzinger C (2016): Reproducibility of resting state connectivity in patients with stable multiple sclerosis. PloS One 11:e0152158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Mumford JA, Nichols TE (2011): Handbook of Functional MRI Data Analysis. Cambridge University Press. [Google Scholar]
- Roberts S (1959): Control chart tests based on geometric moving averages. Technometrics 1:239–250. [Google Scholar]
- Robinson L, Wager T, Lindquist M (2010): Change point estimation in multi‐subject fMRI studies. NeuroImage 49:1581–1592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson L, Atlas L, Wager T (2015): Dynamic functional connectivity using state‐based dynamic community structure: Method and application to opioid analgesia. NeuroImage 108:274–291. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Ruiz S, Buyukturkoglu K, Rana M, Birbaumer N, Sitaram R (2014): Real‐time fMRI brain computer interfaces: Self‐regulation of single brain regions to networks. Biol Psychol 95:4–20. [DOI] [PubMed] [Google Scholar]
- Ryali S, Chen T, Supekar K, Menon V (2012): Estimation of functional connectivity in fMRI data using stability selection‐based sparse partial correlation with elastic net penalty. Neuroimage 59:3852–3861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakoglu U, Pearlson GD, Kiehl KA, Wang YM, Micheal AM, Calhoun VD (2010): A method for evaluating dynamic functional network connectivity and task modulation: Application to Schizophrenia. Magn Reson Mater Phys Biol Med 23:351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott G, Hellyer P, Hampshire A, Leech R (2015): Exploring spatiotemporal network transitions in task functional MRI. Hum Brain Mapp 1348–1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp D, Beckmann C, Greenwood R, Kinnunen K, Bonnelle V, De Boissezon X, Powell J, Counsell S, Patel M, Leech R (2011): Default mode network functional and structural connectivity after traumatic brain injury. Brain 134:2233–2247. [DOI] [PubMed] [Google Scholar]
- Smith S (2002): Fast robust automated brain extraction. Hum Brain Mapp 17:143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith S, Fox P, Miller K, Glahn D, Fox M, Mackay C, Filippini N, Watkins K, Toro R, Laird A (2009): Correspondence of the brain's functional architecture during activation and rest. Proc Natl Acad Sci USA 13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith S, Miller K, Salimi‐Khorshidi G, Webster M, Beckmann C, Nichols T, Ramsey J, Woolrich M (2011): Network modelling methods for fMRI. Neuroimage 54:875–891. [DOI] [PubMed] [Google Scholar]
- Smith S, Hyvärinen A, Varoquaux G, Miller K, Beckmann C (2014): Group‐pca for very large fMRI datasets. NeuroImage 101:738–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song J, Desphande A, Meier T, Tudorascu D, Vergun S, Nair N, Biswal B, Meyerand M, Birn R, Bellec P, Prabhakaran V (2012): Age‐related differences in test‐retest reliability in resting‐state brain functional connectivity. PLoS One 7:e49847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC (2004): Organization, development and function of complex brain networks. Trends Cogn Sci 8:418–425. [DOI] [PubMed] [Google Scholar]
- Stins JF, Tollenaar MS, Slaats‐Willemse DI, Buitelaar JK, Swaab‐Barneveld H, Verhulst FC, Polderman TC, Boomsma DI (2005): Sustained attention and executive functioning performance in attention‐deficit/hyperactivity disorder. Child Neuropsychol 11:285–294. [DOI] [PubMed] [Google Scholar]
- Van Den Heuvel M, Pol H (2010): Exploring the brain network: A review on resting‐state fMRI functional connectivity. Eur Neuropsychopharmacol 20:519–534. [DOI] [PubMed] [Google Scholar]
- Van Essen D, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss S (2012): The Human Connectome Project: A data acquisition perspective. Neuroimage 62:2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varoquaux G, Craddock RC. (2013): Learning and comparing functional connectomes across subjects. NeuroImage 80:405–415. [DOI] [PubMed] [Google Scholar]
- Varoquaux G, Gramfort A, Poline J, Thirion B (2010): Brain covariance selection: Better individual functional connectivity models using population prior. In: Advances in Neural Information Processing Systems, pp 2334–2342.
- Watts DJ, Strogatz SH (1998): Collective dynamics of small‐world networks. Nature 393:440–442. [DOI] [PubMed] [Google Scholar]
- Weiskopf N (2012): Real‐time fMRI and its application to neurofeedback. Neuroimage 62:682–692. [DOI] [PubMed] [Google Scholar]
- Weissenbacher A, Kassess C, Gerstl F, Lanzenberger R, Moser E, Windischberger C (2009): Correlations and anticorrelations in resting‐state functional connectivity MRI: A quantitative comparison of preprocessing strategies. NeuroImage 1408–1416. [DOI] [PubMed] [Google Scholar]
- Whyte J, Polansky M, Fleming M, Coslett HB, Cavallucci C (1995): Sustained arousal and attention after traumatic brain injury. Neuropsychologia 33:797–813. [DOI] [PubMed] [Google Scholar]
- Yeo BT, Krienen F, Sepulcre J, Sabuncu M, Lashkari D, Hollinshead M, Roffman J, Smoller J, Zöllei L, Polimeni J (2011): The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol 106:1125–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilverstand A, Sorger B, Zimmermann J, Kaas A, Goebel R (2014): Windowed correlation: A suitable tool for providing dynamic fMRI‐based functional connectivity neurofeedback on task difficulty. PloS One 9:e85929. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


