Figure 1.

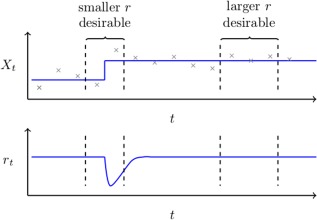
Top: Measurements of a non‐stationarity univariate random variable, ${\mathit{X}}_{\mathit{t}}$, are shown in grey together with the true mean in blue. This figure serves to highlight how the optimal choice of a forgetting factor or window length may depend on location within a dataset. It follows that in the proximity of the change‐point we wish $\mathit{r}$ to be small in order for it to adapt to change quickly. However, when the data is itself piece‐wise stationary, we wish for $\mathit{r}$ to be large in order to be able to fully exploit all relevant data.

Bottom: An illustration of how an ideal adaptive forgetting factor would behave; decreasing directly after a change occurs and quickly recovering thereafter. [Color figure can be viewed at http://wileyonlinelibrary.com.]