Quantifying Gauche Defects and Phase Evolution in Self-Assembled Monolayers through Sessile Drops

Abstract

Self-assembled monolayers (SAMs) are widely used in surface modifications, specifically in tuning the surface chemistry of materials. The structure and properties of SAMs have been extensively studied often with sophisticated tools, even for the simplest n-alkanethiolate SAMs. In SAMs, especially in linear n-alkanethiolates, the properties are dependent on the chain length, which is best manifested in the so-called odd–even effect, a simple yet not fully understood phenomenon. One main challenge is fully delineating the origin of length-dependent properties, which can be due to the structure (ideal SAMs), defect evolution, or substrate-molecule effects. This study demonstrates that utilizing the wetting behavior of polar (water) and nonpolar (hexadecane (HD)) solvents on n-alkanethiolate SAMs formed on ultraflat gold and silver surfaces, the evolution of chain-length-dependent gauche defects can be revealed and parameterized through a newly defined dimensionless number (χ). The observation of the odd–even effect in hydrophobicity, however, depends on the thiol chain length, and it was only observed on longer-chain (>C₈) molecules. The trend in this odd–even effect demonstrates that there are three main transitions in the nature of wetting, hence structure, across n-alkanethiols. From wetting with HD, the role of dispersive components in wetting reveal that the SAMs are dynamic, which we attribute to rotations associated with previously reported evolution in gauche defects and changes in packing density. Therefore, from re-expression of the Young–Dupre equation, we define a new dimensionless number associated with molecular conformations, whose periodicity mirrors the energetics of Goodman’s conformations of n-alkanes in unbound states and associated four- or two-twist turns. Therefore, we infer that the evolution in surface energy is largely due to molecular conformations and associated relaxations of the bound thiolates.

Introduction

Self-assembled monolayers (SAMs) are two-dimensional materials that have shown potential for broad applications in surface science and nanotechnology. These applications include sensing, molecular electronics, plasmonics, and surface modifications.¹⁻⁷ Alkanethiolate SAMs have a simple molecular structure and chemical composition; hence, they are experimentally⁸⁻¹³ and theoretically¹⁴⁻¹⁸ well studied. Understanding the structure and properties of SAMs has been plagued by some inconsistencies¹⁹⁻²¹ or has suffered under some generalized “truths” that, in part, has hampered the application of this rather potentially useful technology. Recent advances in re-characterization of n-alkanethiolate SAMs through either fundamental wetting studies²¹⁻²⁵ or functional devices^1,26,27 has brought to light the need to re-assess the assumed “facts” about SAMs. Fundamental properties of interest include: (i) hydrophobicity and the associated odd–even effect, (ii) nature of the unbound (surface-exposed) interface upon SAM formation, (iii) coupling between surface and bulk properties in defining SAM properties, (iv) effect of a substrate (chemistry, faceting, roughness, etc.) on the nature of the SAMs, (v) role of defects and the effect of molecular length on defect density—especially those related to molecular conformations, like gauche defects (a type of defect caused by molecular rotation into its corresponding gauche conformer),^2,28 and (vi) phase evolution (liquid-like or solid-like) with increase in the size of the molecules forming the SAMs.^2,28 The observed overinterpretation or generalization about the properties of the SAM was, in part, due to the lack of state-of-the-art tools in characterization and/or fabrication, coupled with an inability to fabricate ultraflat surfaces (and/or surfaces with tunable morphologies at low roughness), more than two decades ago. Recently, new approaches and tools have emerged that allow for improved surface fabrication and characterization. Improved methods of modeling or processing surface-generated data, coupled with multipronged experimental and theoretical tools, have led to the improved understanding of surface and interface. With advances in the quality of substrates, we believe that this is an opportune time to revert back to simplicity and deploy fundamentally simple and basic tools to expand our understanding of SAMs, hence extend their adoption as a platform technology.

We^25,29 and Nijhuis²⁷ have recently demonstrated that there are, potentially, multiple transition points in the properties of monolayers, albeit using different approaches. Where the substrates are ultraflat and molecules pure, the transitions in physical properties like wetting can only be translated to be due to changes in the nature of the SAM. There are three main sources of structural changes in a SAM, viz.: (i) the SAM formation process—because this is an equilibration process, lack of ample time for the system to interrogate the free-energy space during SAM formation can lead to nonequilibrium structures. The SAMs are therefore always formed in solutions in which the solubility of the thiol is not very high (low ΔG_m) to drive/promote surface attachment. (ii) The size of the molecule— SAMs’ packing depends on both primary (substrate-molecule) and secondary (interchain) bonds. The latter, though weak (∼1 kJ/mol for van der Waals interactions), affects the nature of defects, phase/crystallinity, and stability of the SAM.^8,16,30 (iii) The substrate—the morphology and chemistry of the substrate affect the quality of the SAM. The effect of surface morphology has recently been shown to be dependent on the size of the defects (primarily grain boundaries in ultraflat surfaces) and the size of the molecules forming the SAM.^27,25,31

Background

A SAM is composed of three parts, namely, the terminal (surface-exposed) moiety, a spacer (often alkyl chains), and an anchoring/head group (often a thiol that forms a bond with the Au/Ag substrate), as schematically shown (Figure 1a). Owing to the varying number of repeat units in the molecules making up the SAMs, the tilt angles of the terminal CH₃ (or CH₂CH₃) groups are different between SAMs with odd (SAM^O) or even (SAM^E) numbers of non-H atoms along the chain (for brevity and clarity, these are abbreviated as total number of C for n-alkanethiolate SAMs). Therefore, this difference in the tilt angle can result in the odd–even oscillation in SAM properties, such as wetting, charge transport, thermal, and mechanical properties.^{15−17,21−23,26,32,33}

Figure 1.

Background data on the progress in understanding SAMs. Schematics of an n-alkanethiolate SAM formed on an Au(111) surface. (a) Oversimplified illustration of SAMs assuming that n-alkanethiol molecules were directly adsorbed onto high-symmetry sites on Au (111). (b) Widely acknowledged (√3 × √3)R30° structure of alkanethiolate SAMs on Au(111). (c) Roughness-dependent limit to the odd–even effect as captured by hydrophobicity.²³ (d) Dependence of the odd–even effect on the nature of the probe liquid; wetting with apolar liquids shows odd–even oscillation even with rough surfaces.²⁴ (e) Substrate effects on the odd–even effect oscillation in wetting for n-alkanethiolates are dominated by SAMs with odd number of carbons and show convergence at propanethiolate SAM.²⁵ (f) Spectroscopic evidence (sum-frequency generation (SFG)) shows no odd–even oscillations for the vibration peak intensities on rough surfaces, although a disappearing inverse zigzag oscillation is observed for peak width on both rough and smooth surfaces.²⁹ This captures the differences in the evolving interface and bulk structures.

Wetting, a characteristic equilibria-based surface/interface property, often captures subtle differences in properties of surface-exposed moieties, like their conformations or the overall packing density of an SAM.^12,34−37 Wetting depends on both surface texture and chemistry. It is, therefore, imperative that differences in the orientation of terminal moieties in SAM^O and SAM^E will manifest as a zigzag oscillation in the contact angles with increasing molecular length, in part due to changes in surface topology. The odd–even effect in SAMs wetting, however, is highly dependent on the identity and/or texture of the substrate on which the SAMs are fabricated.^21,23

n-Alkanethiolate SAMs on an Au surface show a close-packed lattice of (√3 × √3)R30° at saturation coverage (1/3 monolayer) (Figure 1b).² With more complex substrate-molecule structures being observed from experiments and models,³⁸⁻⁴⁰ a secondary structure, c(4 × 2)/(3 × √3), has been reported for shorter-chain n-alkanethiolates. Because the length of the molecule (number of carbons in the chain, n) also affects the structure and hence properties of the SAMs,^8,41 there must be differences in properties that are chain-length dependent^14,16 and therefore some phase changes. Guo and Li,⁸ for example, proposed a unified model to address the phase transition from propanethiol (C₃) to butanethiol (C₄). They claimed that, as expected, van der Waals interactions increase with the molecular length, leading to a rearrangement of the alkyl chains and hence a phase change. They also explained that the ability to tilt and twist with longer-chain molecules (at least ≥C₉) gave rise to the formation of the commonly acknowledged (√3 × √3)R30° top surface structure. Fenter and Eisenberger,⁴² however, reported two distinct regimes, viz., SAMs with n > 14 and n < 14, through structure and phase changes. They also observed a temperature-dependent coexistence between “solid” and “liquid” phases of SAMs. In a related study, Jabbarzadeh and co-workers,¹⁶ through molecular dynamics simulations, noted that gauche defects are more likely in short chains, n ≤ 7, than in the longer homologues. This chain-length-dependent evolution of gauche defects showed an odd–even effect for molecules with 12 ≤ n ≤ 15. This chain-length dependence in gauche defects, however, plateaus out for longer chains, n ≥ 15, with defect densities diminishing at this point.

Despite the reported chain-length dependence of SAM structures, various studies characterized the surface and/or bulk properties of monolayers across all molecular length scales and compared the properties assuming these SAMs are members of the same structural homologues. Prato et al.⁴³ observed from optical characterization (optical spectroscopic ellipsometry) that the thickness of alkanethiolate SAMs (C₆, C₁₂, and C₁₈) does not scale up with the chain length. With a longer chain length, the thickness scales more rapidly with an alkyl chain, indicating a chain-length dependence in the general SAM structure. Recently, however, Nijhuis and co-workers²⁷ have shown that the charge transport properties of SAMs with n > 10 are significantly different than those of shorter homologues. Interestingly, a C₁₀n-alkanethiolate SAM is ∼1 nm thick, which is equivalent to the recently reported roughness-dependent limit to observation of the odd–even effect in n-alkanethiolate SAM hydrophobicity (Figure 1c). We inferred that the equivalence in the SAM thickness (Nijhuis) and the roughness-dependent limit is not a coincidence but rather a manifestation of a compliance limit in the SAMs’ ability to dominate the interface properties, which may in turn indicate either loss of the liquid-like property or a structural phase transition in the SAM. The difference in the SAM structure, however, would best manifest in phase changes as reported by Guo and Li.⁸

We recently showed that the spectroscopic (SFG) signals of the terminal CH₃ in n-alkanethiolate SAMs differ for SAMs with n < 13 and n > 13 (Figure 1f).²⁹ This SFG transition coincides with the Jabbarzadeh’s transition¹⁶ in the manifestation of the gauche defects in SAMs. We inferred that a phase transition may be occurring at this chain length, even though others⁴⁴ have inferred that C₉–C₁₈ SAMs are solid-like. In a recent report, we²⁵ have also demonstrated that substrate-driven odd–even differences in SAM hydrophobicity across Au and Ag disappear at chain lengths ≤C₃, which suggests that at this chain length, the interface properties are not solely dictated by the SAM (Figure 1d). We noted that at such low chain lengths, the SAMs are no longer hydrophobic but they wet with water (static contact angle <90°). Guo and Li⁸ had also noted that the structures of the propanethiol and butanethiol SAMs are different, and as such, the change in wetting properties and loss of substrate-dependent odd–even effects attests to the difference across this C₃–C₄ transition. In a series of reports,^21,23−25 we showed that the wetting properties of SAMs not only depend on the substrate identity and morphology but also on the probe liquid. We noted that roughness dependence of the odd–even effect shows a transition at 1 nm for hydrophobicity (Figure 1c),²³ but we did not observe any transitions for oleophobicity (Figure 1d).²⁴ This suggests that the SAM interfaces can yield a significant amount of information when probed with liquids with polar and nonpolar contributors to their surface tension. The dichotomy in the n-hexadecane (HD) and water wetting properties also points to the need for specificity and/or a reference parameter, in defining stereo-structure properties like the odd–even effect.

A comprehensive re-evaluation of the nature and properties of SAMs across all chain lengths is therefore needed, to better advance the utility of this fundamental platform. We hypothesize that on the basis of the observed structure and properties of SAM, the nature of the interface created by short-chain (≥C₄) SAMs, assuming an equilibrium, should be significantly different from those derived from medium-sized (C₉–C₁₄) or longer (≥C₁₅) SAMs. To evaluate the nature of the created interface, we desired to deploy simplicity and therefore measured static contact angles on short-chain SAMs. The static contact angle, a capture of the equilibrium wetting state, is information rich, where the nature of an interface is desired. Herein, we report a comparative study of the static wetting properties of n-alkanethiolate SAMs in the C₃–C₁₆ chain length range.

Results and Discussion

Because the quality of the SAM and hence its corresponding properties are highly dependent on the substrate (identity, roughness, and morphology),^2,27,31,45 all SAMs were fabricated on ultraflat surfaces. The well-studied ultraflat template-stripped gold and silver surfaces (Au^TS and Ag^TS) were used as substrates.⁴⁶ These two substrates were characterized by atomic force microscopy (AFM), as shown in Figure 2a. The root-mean-square roughness (R_RMS) is thus estimated, with Au^TSR_RMS = 0.41 ± 0.04 nm and Ag^TSR_RMS = 0.64 ± 0.06 nm. The power spectra density (PSD), a parameter used in characterizing the surface topology,^47,48 is also estimated as 0.14 and 0.25 nm² for Au^TS and Ag^TS, respectively, whose values are comparable to those of previous reports.^21,23 The three-dimensional (3D) view of the surface from AFM (Figure 2b) also shows that both surfaces are ultraflat with Ag^TS slightly rougher than Au^TS. Back-scattering SEM images (Figure 2c) indicate that both the Au and Ag surfaces are polycrystalline. Wide-angle X-ray diffraction patterns (Figure 2d), however, show that both Au and Ag have one significant peak, indicating that the faceting for both surfaces is dominated by the (111) direction.

Figure 2.

Surface characterization of the substrates used for SAM formation. (a) AFM images of the substrates, from which the rms roughness and PSD were estimated. (b) 3D demonstration of the surface texture from AFM. (c) Back-scattering SEM images of the template-stripped gold surface (Au^TS) and silver (Ag^TS) surface. (d) Wide-angle X-ray diffraction patterns of the two substrates, indicating a dominance of the (111) orientation.

Overview: Comparison of Hydrophobicity between Short- and Long-Chain SAMs

Short-chain alkanethiol molecules, S(CH₂)₂CH₃–S(CH₂)₈CH₃ (abbreviated as C₃–C₉), were used to form SAMs. Static contact angles (θ_s) of water drops (1 μL) on the SAMs were then obtained. For both Ag^TS and Au^TS, a rapid drop in the contact angle was observed at the C₃–C₄ chain length (Figure 3). Figure 3 shows that the average contact angles on short-chain (C₄–C₈) SAMs formed on Au^TS increase linearly and show no odd–even oscillation unlike in the homologous longer (C₁₀–C₁₆) SAMs.^23,24 An analogous study on Ag^TS showed a slightly different behavior, in that the data are not fully linear, although the slight variations in odds and evens is within the resolution of contact angle measurements. Besides the lack of an odd–even effect for short-chain SAMs (C₃– C₈/C₉), the contact angles are relatively lower than those derived from longer-chain SAMs. The contact angle on Ag^TS, as expected, is relatively lower than that on Au^TS, especially on short-chain SAMs, despite the fact that the packing density of molecules on Ag is slightly larger than that on Au.²¹ We note that in lieu of the odd–even effect, the contact angles increase with the increase in the chain length, and for C₄–C₉, a linear trend is observed.

Figure 3.

Water contact angle on SAMs formed on template-stripped gold (Au^TS) and silver (Ag^TS) surfaces. (a) Contact angle measured on short-chain SAMs (C₃–C₉) formed on Au^TS compared to that on long-chain (C₁₀–C₁₆) SAMs, derived from ref (23). (b) Contact angle measured on C₃–C₉ SAMs formed on Ag^TS compared to that on long-chain (C₁₀–C₁₆) SAMs from ref (24).

Chain-Length Dependence in Hydrophobicity of SAMs

On both substrates, the contact angle in general increases with the chain length of the molecules (Figure 3) but seems to asymptote on longer-chain molecules, albeit with emergence of the odd–even zigzag oscillation. The contact angle data can be broken down into three regimes, viz.: (i) the hydrophilic region (contact angle <90°); (ii) the linear regime with no odd–even effect (C₄/C₅–C₈ for Au^TS and C₄–C₉ for Ag^TS); (iii) the odd–even regime (C₉/C₁₀–C₁₆).

Understanding the Three Regimes

Surface wetting and hence the static contact angle (θ_s) are dependent on two main forces, the dispersion force (γ^d) and polar force (γ^p).^23,49 On the basis of the Owens–Wendt–Kaelble model for work of adhesion,⁵⁰ the cosine of the static contact angle in Young–Dupre’s equation⁵¹ can be expressed in terms of the liquid surface tension and the liquid- or surface-specific γ^d and γ^p (eq 1).

1

2

where LG and SG refer to the liquid–gas and solid–gas interfaces, respectively, and γ is the surface tension. By simplifying the equations using energy proportionality parameters for dispersive and polar 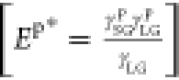interactions, we obtain eq 2, which relates the contact angle to a dimensionless term.

For wetting with polar probe liquids like water, the contact angle (θ_s) increases with a decrease in E^d* or E^p*, that is, a decrease in overall surface tension. The surface normal dipole in n-alkanethiolate SAMs generally increases with the molecular chain length,^16,18 leading to an increase in E^p* with the molecular chain length.^21,23 In contrast, the dispersive component, E^d*, in SAMs decreases with the molecular chain length due to constrained molecular vibrations induced by the increased interchain secondary bonds and decreased gauche defects in longer-chain molecules,^44,52 that is, the SAM becomes more rigid.

Zone 1: Short Chain Length ≤ S(CH₂)₂CH₃

The ability to isolate this region from the rest stems from three separate sets of evidence and, as such, is a prediction rather that is solely supported by data provided herein. The evidence supporting this inference is: (i) from Figure 2, SAMs of C₃ on both Au^TS and Ag^TS significantly deviate from the linear trend of the preceding homologues by showing a significantly lower contact angle than longer ones (≥C₄). Of note also is the fact that hydrocarbons are generally hydrophobic, but C₃ SAMs are hydrophilic. This switch in wetting properties can only be rationalized from either poorly formed SAM or changes in the electrostatic potential of the terminal CH₃ due to inductive effects from the metal–S bond or analogous effects (like σ–σ* hyperconjugation or metal–molecule orbital mixing extending up to the C₃). (ii) In addition, and as we previously reported,²⁵ the values of the contact angle from C₃ SAMs on Au^TS and Ag^TS are comparable, and any substrate-dependent wetting properties disappear at ≤C₃. (iii) The structures of C₃ and C₄ thiolate SAMs on Au show a significant difference in their organization and packing density.⁸ Higher adsorption energy of C₃ to the substrate relative to the longer congeners¹⁴ and the lack of considerable contribution from the interchain van der Waals force⁸ can give rise to poorly formed SAMs and hence ill-defined interfaces. This unusual behavior of very short chains (≤C₃) is in good agreement with the previously predicted structural phase change from C₃ to C₄ SAMs.^8,14 From the observed hydrophobic–hydrophilic switch in wetting, the disappearance of the odd–even effect, and the physical characterization studies, lead us to hypothesize that the structure of the SAM changes across the C₃–C₄ chain length.

Intermolecular dipolar repulsive interactions in SAMs arise from interactions between the permanent dipole of molecules and the bond to the metal substrate.^53,54 When the chain length is limited (here <C₃), the disordered molecular assemblies have fairly significant dipolar repulsive interactions, which can dominate SAM properties over the limited van der Waals interactions in short-chain molecules. As a result, contrary to the long-range re-organization of tail groups into a densely packed surface structure in long-chain SAMs,⁴⁰ the short-chain molecules are adsorbed almost without “through space” interactions and therefore are not able to form well-defined interfaces. Ulman and co-workers observed that terminal moieties from short-chain SAMs were “masked” by conformational instabilities.⁵⁴ Besides, it has been observed that the highly mobile/unstable features in short-chain SAMs facilitate surface migration (diffusion), where the molecules in these SAMs can “walk” or “hop”.⁵⁵ In light of this behavior, we postulate that the water molecules can also imbibe into the SAMs in the absence of a stable interface leading to improved wetting. Besides these studies, the nature of the thiol–metal bond has been hypothesized to bear a strong dipole, which could lead to a significant inductive effect. Alternatively, and owing to the covalent nature of the thiol–metal bond, σ–σ* hyperconjugation between the S-metal σ* orbital and the C₂–C₃ σ bond can be envisioned. Hyperconjugation between σ_S–M^* and σ_C2–C3 orbitals in SAMs is possible, in part due to the syn-periplanarity between σ_S–M and σ_C2–C3 bonds. This syn-periplanarity is independent of the substrate (Au vs Ag) and can account for the previously predicted^21,23−25 and now empirically confirmed loss of substrate dependence of the odd–even effect for n ≤ 3 SAMs. For these reasons, we infer that n ≤ 3 SAMs do not bear analogous interface characteristics to the longer homologues, and as such, they are not analogues to their longer congeners.

Besides poorly formed SAMs, proximity to the metal–S bond can lead to significant inductive effects, leading to enhanced polar interactions across the C₃ SAM–water interface. Ratner and co-workers⁵⁶ theoretically showed that there is significant orbital mixing between the metal and the molecule upon thiolate binding on Au, and the large electronegativity differences between the metal and thiol can lead to significant inductive effects either near the surface or may significantly extend into the molecule. Although these inductive effects are a possibility (and have been inferred from theoretical studies as mentioned above), we exercise caution in inferring that they are the major contributor to the C₃ SAM hydrophilicity as more direct evidence is needed to ascertain this.

Zone 2: Medium Chain Length SAMs (C₄–C₈/C₉)

The increasing contact angle in the region of chain length C₄–C₈/C₉ suggests that there is probably a gradual increase in the rigidity of the SAM, albeit not sufficient to induce a phase change. The low enthalpic gain upon self-assembly is not sufficient to overcome molecular vibrations under ambient conditions; hence, there are higher gauche defects in short-chain (C₄–C₈/C₉) SAMs¹⁶ and therefore a likely less-dense packing leading to a liquid-like SAM. From this argument, we can infer that higher degrees of freedom allow for maximizing dipole–dipole (polar–polar) interactions between the SAM and water droplets and hence the ability for water to spread on an otherwise chemically hydrophobic surface (i.e., interface dominated by hydrocarbons). We observe that as the number (hence, the total enthalpic gain) of possible interchain interactions increases (increase in the number of H atoms), a decrease in hydrophobicity is observed, which eventually renders the surface more hydrophobic with increasing chain length. To further support this argument, evaluation of oleophilicity shows a similar trend, suggesting that a similar structure–property evolution is also possible for apolar interactions between the SAM and a nonpolar solvent, HD. HD-derived θ_s shows a linear increase for short-chain SAMs, followed by an odd–even oscillation with increasing chain length. From SFG spectroscopic studies, it has been shown that the intensity of asymmetric stretching of the terminal CH₃ group increases generally with the chain length, which is mostly due to a decreasing density of the gauche defect.^29,44

We infer that these results, at a minimum, suggest that (i) the interface in medium chain length SAMs is evolving with the increase in the length, (ii) these SAMs are likely conformal, that is, they can deform in response to the liquid contacting them (i.e., these SAMs are dynamic, hence liquid-like), (iii) the interfacial properties of these short-chain SAMs are significantly different from those of higher chain lengths. We therefore infer that SAMs of medium-length molecules are liquid-like as previously suggested.¹⁶

Zone 3: Transition Regime (C₈/C₁₀–C₁₃)

A substrate dependence transition is observed in this zone, with Au transitioning at C₈ and Ag transitioning at C₁₀. A clear odd–even effect emerges at C₈/C₁₀. Although one can argue that for Ag the oscillation starts at C₆, the slight differences between the SAM^O and SAM^E are stochastic in nature and statistically indistinguishable (C₆ ≈ C₇ and C₈ ≈ C₉), therefore not indicative of a reliable zigzag oscillation. A clearer zigzag oscillation emerges from C₈ (for Au) and C₁₀ (for Ag), albeit showing asymmetric gain with transition from SAM^O to SAM^E compared to that of SAM^E to SAM^O, as previously described.^21,23−25 We infer that this region represents a transition zone bearing characteristics of the preceding regime and the one ahead of it. In that case, the gradual increase in contact angles is indicative of the continued evolution of the interactive effects captured in the preceding zone (zone 2), whereas the odd–even oscillation is indicative of what happens with increasing chain length (zone 4). It can be observed that the differences between two consecutive molecules in the series is larger among the shorter analogues and declines with the increase in the molecular length. An elaborate discussion on this behavior has been given in preceding works.²³⁻²⁵ Within this region, spectroscopic data indicate that the local environment of the CH₃ terminal group changes with changes in the molecular length and shows an odd–even oscillation irrespective of the degree of order or disorder (based on the nature of substrate morphology), suggesting that the molecules are dictating how they group on the surface irrespective of the limitations to the nature of the surfaces—that is, the molecule is dictating the nature of the interface. In an analogous study, Nijhuis and co-workers demonstrated that a C₁₀n-alkanethiol is sufficient to overcome surface defects, an observation that is in line with our inference.

Zone 4: Symmetric Odd–Even Regime (≥C₁₄)

Beyond the transition zone, the zigzag odd–even oscillation in contact angles asymptotes and becomes symmetric, as previously observed.^23,24 We infer that this asymmetry is due to the SAMs becoming crystalline/well-ordered; hence, the only differences in their interfaces are the orientation of the terminal CH₃. In an earlier spectroscopic study,²⁹ this enhanced order manifested as a gradual linear decay in the peak width and a loss of the odd–even oscillation in the peak width. We believe that the change from a gradual increase in the odd–even oscillation in the SFG signal peak width reported previously is a manifestation of the increased order, which leads to increased homogeneity in the local chemical environment of the terminal CH₃²⁹ and manifests here as a symmetric odd–even zigzag oscillation in wetting.

Odd–Even Effect, Dispersive Forces versus Molecular Chain Length

The contact angle of a nonpolar liquid, HD, was measured on all molecules on gold substrates and was also compared with the water contact angle, as shown in Figure 4. The contact angle gradually increases then asymptotes, and shows an odd–even effect, with increase in the molecular length (Figures 3 and 4). A close look at zone 3, however, reveals that the contact angle gradually increases when the probe liquid is water^23,24 and starts to plateau when the chain length is >C₁₃. From eq 2, it is known that the contact angle depends on both the dispersive and the polar components of surface tension; hence, the interaction energy (or wetting behavior) can be captured by the contact angle (θ_s). We infer that this gradual and reproducible increase^19−25,57 is due to a change in the interaction energy between the SAMs and water, which in this case would indicate a change in the nature of the molecules with increasing molecular length. As stated, however, eq 2 fails to parameterize the changing dynamics at the interface, partly due to its focus on energy. A dimensionless number is therefore needed to qualitatively capture the molecular changes associated with these SAMs.

Figure 4.

Contact angle of HD compared to that of water on SAMs formed on Au^TS. Contact angles of C₁₀–C₁₆ are obtained from ref (23).

From eqs 1 and 2, by rearranging the Young–Dupre equation, we define a new parameter (a dimensionless number), χ_c, on the basis of proportional energetic contributions (both polar (E^p*) and dispersive (E^d*) components of surface tension) of the surface–liquid interactions (eq 3).

3

For nonpolar HD, the polar component is negligible (γ_LG^p = 0); hence, contribution to wetting by polar–polar interactions is zero, E^p* = 0, as such . Neglecting the polar component in the equation above, we can re-express it for HD as shown below (eq 4). Because both γ_LG and γ_LG are constant for any apolar liquid, for brevity and clarity, we represent them as a constant, α, to illustrate that only proportional contributions of dispersive forces in the SAM (γ_SG^d) affect the extent of wetting (eq 4); hence, any asymmetry in wetting can only result from changes in the surface energy.

4

Evolution in contact angles with increase in the molecular chain length would therefore imply that the dispersive component of the surface energy of these SAMs is a function of the number of repeat units (carbons in n-alkanethiols), that is, γ_SG^d = f(n).^23,24 We can, therefore, re-express eq 4 as χ_c² α · f(n). A plot of χ_c² against the chain length can help delineate the evolution of the dispersive component of the surface energy in SAMs with increasing molecular length, and this is captured in Figure 5. The correlation between the chain length (n) and dispersive interactions shows that, as expected, SAM^O and SAM^E segregates into two groups, in which χ_c² exponentially decays with increase in the chain length (the lines are a guide to the eye and not a fit to a model). C₁₃ is off the fits, either due to the compound (C₁₃ is synthesized in-house but the rest are purchased from Sigma-Aldrich and used as received) or due to the different nature of C₁₃ SAMs (C₁₃ is the transition point between waxy to crystalline and hence small temperature perturbations can lead to a change in the nature of the interface). We have also spectroscopically observed that a transition occurs across the C₁₃ chain length,²⁹ and this transition may lead to an interface that is more sensitive to the dispersive forces compared with the polar forces, hence the difference in the odd–even effect between water and HD (Figure 4). From the trends, however, we observe that the contribution to the surface dispersive forces are inversely proportional to the chain length and can be summarized as (eq 5)

5

where A, t, and ε₀ are fitting parameters, and from this expression, it can be observed that χ_c² ≠ 0 at any point (i.e., no x axis intercept because it requires that 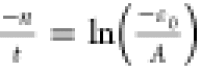, an invalid mathematical solution). It therefore follows that, from a theoretical point and on the basis of preceding arguments, at n = 0, χ_c² = A + ε₀ (a constant) in the absence of any carbon atoms. Re-expressing eq 5 into a log scale gives

6

Figure 5b, as expected from eq 6, shows a linear chain-length dependence of the χ_c², indicating that the evolution in dispersive (van der Waals-type) interactions at the liquid–SAM interfaces have a linear logarithmic relation. An odd–even oscillation in the dispersive interactions component of surface tension is observed for SAMs derived from n-alkanethiols, whose magnitude increases with the increasing molecular length. From the linear fits in Figure 5b, the two lines merge at approximately 3, indicating the disappearance of the odd–even effect at C₃, which correlates well with early predictions²⁵ and our inference that SAMs (≤C₃) belong to a different regime.

Figure 5.

Dispersion interactions in wetting is correlated to the chain length of the molecules. (a) For HD, the dispersion interactions are fitted, showing a correlation with the chain length of the molecules and exhibiting an odd–even effect. (b) In the log scale, the dispersion energy minus a constant that is derived from the above fits show a linear relation with the chain length of the molecules.

In addition, we also observed that χ_c² seems to plateau beyond C₁₄ in Figure 5a,b. We attribute this to increased SAM crystallinity; therefore, owing to a decrease in rotational degrees of freedom, an increase in the chain length has an insignificant effect on the van der Waals interaction and hence the wetting properties. A recent report on a spectroscopic (SFG) study of the odd–even effect in n-alkanethiolate SAMs²⁹ shows that evolution of the amplitude of the terminal CH₃ stretch for SAM^E was significantly smaller than that for SAM^O, which indicated a less rigid orientation of the dipole moment at the interface (hence, a less rigid SAM), in line with the observed odd–even trends in the dispersive interactions observed here (Figure 5a). In addition, the two distinct regimes in peak width (<C₁₃ and >C₁₃) from SFG studies also correlate well with the observed plateau at C₁₄ in dispersive interactions. Because the contribution of dispersive interactions decreases with an increase in the molecular chain length, in general, we can infer that the molecules get more rigid (reduced degrees of freedom) and hence a convergence occurs in the orientation states of the terminal CH₃, leading to a significant difference in the orientation of these groups at the interface for SAM^O and SAM^E. Increased rigidity, in turn, allows for easier differentiation between SAM^O and SAM^E through wetting. We therefore infer that attenuated molecular vibrations lead to minimization of interfacial coupling, hence poor coupling in the dispersive components of the interfacial surface energy (molecular vibration-dependent secondary bonding) and hence more defined differences in γ_SG versus γ_LG. By definition, Gibbsian surface tension (free energy per unit area) is the difference between surface energy and surface entropy (γ = U_surface – S_surface),⁵⁸ and as such, increased molecular vibrations or orientation states (total number of conformations possible) will increase the entropy at the interface leading to a decrease in the overall surface tension. This basic definition of surface tension allows us to further infer that the unbound surface of shorter SAMs (higher vibrations and larger number of conformational states) is, therefore, less ordered (supported by SFG studies); otherwise, a decrease in θ_s^water and a concomitant increase in θ_s are expected. The gradual decline in contact angles for both polar and nonpolar probe liquids suggests that there are other changes occurring in the system besides interfacial entropy. This inference is further supported by an increase in contact angle distributions (standard deviations) as the chain length decreases.

The fits in Figure 5b demonstrate two different rates of decay in the χ_c with the chain length for SAM^O and SAM^E. The (χ_c² – ε₀) term captures the structural deviation of an SAM from the ideal well-ordered defect free state and allows us to infer that defects density decays logarithmically with an increase in the molecular chain length. We can infer that, in general, SAM structural properties (such as thickness) are highly dependent on the chain length of molecules used to fabricate them. We can also infer that with longer chain lengths, the molecules are likely to be trans extended; hence, longer-chain SAMs are thicker, as previously observed by Prato and co-workers.⁴³

In addition, Figure 5b demonstrates that the odd–even effect is not symmetric, and more importantly, the dependence of dispersive interactions/surface properties on the molecular chain length is different for odds and evens. In other words, the addition of one methyl group to the spacer (alkyl chain) can contribute differently to the nature of secondary bonding in SAM^O versus SAM^E, which, as we inferred, is attributed to the stereostructural variance of the hydrocarbon tail. These findings correlate well with previous reports about other properties of n-alkanethiolate SAMs. In charge transport behavior of SAM-based molecular junctions, the injection current (J₀) and the contact resistance of the SAM and the electrode (R_C) are different due to different orientations of the terminal groups.^18,26,32,59 Similarly, in charge transport and friction studies, the decay constants, β, for SAM^O and SAM^E are different,^18,26,32,59 wherein the conformational disorder (gauche defects) of the molecules affect the local chemical environment of the terminal moiety, as confirmed through spectroscopic (SFG) studies.²⁹ Similarly, theoretic work in charge transport behavior across alkanethiolate junctions predicted that the odd–even effect is prominent within a certain chain length (10 < n < 19) on silver substrates.¹⁸

Serendipitous Correlation of χ_c with Conformation Dynamics or a Solid Association?

We observe that, although the plots in Figure 5 are not fitted to a specific model, the associated decay (exponential) equations bear a 3- (derived from e^n/3) or 4- (derived from e^n/4) geometric progression (i.e., χ rises by an order of 1) for SAM^O and SAM^E, respectively. This observation is not unique to SAMs but has previously been associated with two global minima in the conformational relaxation of linear hydrocarbons.⁶⁰ In his seminal theoretical work on conformational stability of free hydrocarbons, Goodman observed that C₁₇ (C₁₁ by PM3 simulations) is the longest possible linear hydrocarbon as predicted in the gas phase. The presence of a solvent changes this dynamic on the basis of the solvent used, with a mismatch in solubility parameters favoring more intramolecular interactions and hence folding. Longer-chain hydrocarbons adopt different (folded/rotated) conformations to allow for favorable intramolecular interactions. When the molecules are long enough, they can fully fold back via two main approaches: (i) a four-twist turn that involves maximized intrachain van der Waals interactions across four carbons, allowing the molecules to fully bend onto themselves, and, (ii) the two-twist turn that involves three carbons and two gauche rotations. Goodman demonstrated that the two-twist turn precedes the four-twist turn in the evolution as the chain length increases. In line with Goodman’s observations, we inferred that if the origin of the observed progress is a probabilistic chain relaxation, then embedded within the four-carbon progression are the more accessible two-twist turns (three carbons). The SAM^E were, therefore, separated into two groups, in which the series follows a four-carbon progression (see Figure S3 in the Supporting Information (SI)). When the two four-carbon progression groups are further evaluated, the lower energy three-carbon progression series is observed, as indicated by the fitting parameter, t, and predicted by Goodman on the basis of thermodynamic stability. Therefore, we infer that the decay in χ_c, and associated changes in θ_s are likely due to conformational changes in the hydrocarbon chains, the basis of the widely reported gauche defects. Therefore, we can deduce that χ_c is a gauche defect-associated surface energy parameter. On the basis of this observation, and the strong correlation with Goodman’s study, we also infer that the substrate-independent odd–even oscillations in SFG peak widths can be attributed to these changes in conformations with increasing chain length and is the basis of the observed differences in wetting properties.

Evolution of Hydrophobicity with χ_c

Unlike hexanes or other nonpolar liquids, most molecules bear both polar and nonpolar contributors to their surface tension. Hence, for water, 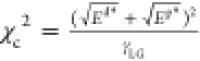because both polar and dispersion interactions contribute to wetting. As shown in Figure 6, chain-length dependency of χ_c² with water for SAMs on Au^TS shows an asymmetric decay segregating into two different regions. The odd–even effect was only observed when n > 8, similar to the observation from the contact angle. For n < 8, a linear decrease in χ_c² was observed, and as previously noted, data from the C₃ SAM did not follow a similar trend. The small odd–even oscillation coupled with low dependence of the wetting behavior on the molecular chain length (despite the associated entropic changes upon chemisorption) implies that, as expected, the dispersive component of surface tension is not the dominating influence in the wetting behavior of water. Because the polar component of surface tension is larger than the dispersive component, we can infer that any SAM property that perturbs polar–polar interactions would have a large effect on the wetting properties of water and is the subject of a different study.

Figure 6.

Chain-length dependence of interactions (χ_c²) in wetting for polar liquids (water).

Big Picture: Understanding Structure versus Chain Length Relations in SAMs

Having gained insights into the role of nonpolar surface interactions in wetting, observing the evolution of wetting with the chain length, and borrowing from earlier studies, a better understanding of SAM properties has been realized. The SAMs’ structures vary with the chain length, as revealed in ellipsometry (thickness),⁴³ STM (the packing structure),⁸ and as simulated in studies of gauche defects (conformational structure).¹⁶ From contact angle measurement, it was demonstrated that the interface properties of the SAMs were significantly chain-length dependent irrespective of whether a polar or nonpolar probe liquid was used. The observed trends in wetting with water and HD are likely due to the structural changes of SAMs with the increase in the molecular chain length.

Therefore, we are able to differentiate four regions in n-alkanethiolate SAMs on the basis of changes in wetting (particularly hydrophobicity) with changing molecular chain lengths (Figure 7). We identify these regions as: (i) pseudoformed interface from SAMs with n ≤ 3, where the limited intermolecular interactions, and potentially inductive or hyperconjugative effects, lead to poorly formed hydrophilic CH₃-terminated interfaces. (ii) Liquid-like SAMs with chain lengths within C₄–C₈/C₉: The van der Waals force gradually increases with the chain length and, with an increase in the molecular length, isolates the interface from any inductive effects that may arise due to the metal–thiol bond. With limited degrees of freedom, and decreasing gauche defects, a more static hydrophobic interface emerges. The emergence of the odd–even effects with longer chain lengths further corroborates this inference, in that, a more defined orientation of the terminal moiety is only attained with longer chains. (iii) Transitional “waxlike” SAMs with the chain length ranging from C₉/C₁₁–C₁₃: SAMs within this range show a clear odd–even effect, although a gradual increase in the contact angle is observed. The contact angles plateau off into a static value for SAM^O and SAM^E. The gradual increase in the contact angles is due to asymmetry in the odd–even oscillation, with changes in contact angles from evens to odds (Δθ_s^E-O) being less than those from odds to evens (Δθ_s^O-E) on Au substrates and vice versa on Ag. As previously observed, this asymmetry is due to changes in the contribution of the dispersive component (γ^d) to the SAM interface and has been associated with increased order/rigidity (Figure 5a).²⁴ (iv) Crystal-like SAMs with chain length >C₁₄: In this region, the contact angles do not change with increasing chain length, although an odd–even oscillation is observed.

Figure 7.

SAM structure, and associated interfaces, varies with chain-length, segregating into four chain length dependent regions (for n-alkanethiolate SAMs) as inferred from wetting behavior. The four regions are associated with degree of order in the SAMs and can be associated with chain-length dependent evolution in molecular conformations.

Conclusions

In n-alkanethiolate monolayers, molecular chain length significantly affects SAM packing, structure and hence properties. Wetting behaviors of n-alkanethiolate SAMs on ultraflat template-stripped surfaces, as captured in a static contact angle in this article, are dependent on the chain length, which is presumed to be due to different interface properties of the SAMs. We infer that the observed differences are due to intermolecular interactions, molecule–substrate interactions, and molecular conformational freedom (hence, gauche defects). From this work, we draw the following inferences:

• (i)The odd–even effect in water contact angle on short-chain SAMs (<C₉) is not observed on the Au^TS surface or the Ag^TS surface. The presence of significant gauche defects and limited enthalpic driving force toward more order, due to the limited number of favorable interchain van der Waals interactions, renders molecules in these SAMs more mobile (we term this as liquid-like) and hence there is no clear distinction between the packing and terminal group orientations in SAM^O and SAM^E. This lack of distinction manifests as disappearance of the odd–even effect with decreasing chain lengths.
• (ii)For brevity and clarity, we define a new simplified dimensionless number, χ_c: This new parameter correlates well with rotational/conformational changes in the molecule and, as such, indicates the evolution of gauche defects in the SAM. This new parameter was deduced from interfacial dispersive forces and is characteristic of the surface under investigation and the length of the chemisorbed molecule. We believe that this new constant will help extend the characterization and hence definitions of various surfaces, allowing comparison of data across different platforms.
• (iii)The dispersion interactions, hence wetting, correlate with surface entropy and not just chemical properties of the terminal group in the SAM: Although all SAMs are derived from n-alkanethiols, which would manifest as CH₃-terminated interfaces, wetting (with HD or water) is more favorable with shorter chains. From the simplified Gibbsian definition of surface tension, that is, surface tension is the difference between surface energy and surface entropy (γ = U_surface – S_surface), we can infer that an increase in the rotational freedom and hence the ability to alter the orientation of the terminal moiety under different probe liquids, will affect the entropic term to minimize the resultant interfacial surface tension. This thermodynamically favorable “relaxation” at the interface manifests as hydrophilicity for the much shorter n-alkanethiolates. The more upright molecules (SAMs on Ag) show a lower surface energy even with a higher packing density (molecules per unit area); hence, C₃–C₅ SAMs are hydrophilic on Ag, whereas only C₃ is hydrophilic on Au.
• (iv)SAMs of molecules with various chain lengths show up to four possible different structural phases. Evaluating the progress in SAM wetting properties across C₃–C₁₆, and borrowing from recent studies from us^22−24,29 and others,²⁷ we observe that (i) C₃ is an isolated case and does not align with the rest. There are two main possibilities, viz., either the SAMs are poorly formed (only seven H atoms, hence low enthalpic gain from secondary interactions) or there are significant inductive effects due to the proximity to the metal–thiol bond. At the moment, we cannot ascertain which of these two hold good in this case, but it is likely that both are contributing. More studies are needed, but on the basis of the substrate dependence studies,²³⁻²⁵ the literature,^8,14 and current studies, we can infer that ≤C₃ SAMs are different than their longer homologs. (ii) A linear regime in the dependence of the contact angle with the molecular length is observed for C₄–C_8/9. We infer that this could be attributed to surface entropy changes due to a gradual linear increase in the enthalpic gain from interchain secondary interactions with the increase in the number of CH₂ moieties. This inference is in line with the decrease in gauche defects observed by Jabbarzadeh and co-workers.¹⁶ (iii) A transition zone between the more liquid-like to the crystalline SAMs, which we refer to waxlike. Inference from wetting and SFG data indicates that C_9/10–C₁₃ SAMs show different properties than the preceding or following homologues. We refer this region as waxlike as it shows properties across the other phases, that is, a gradual increase in the contact angles (albeit nonlinear) and an odd–even effect (albeit asymmetric to account for the increase in contact angles) are observed. (iv) Finally, the increase in the contact angle asymptotes into a linear regime, and the odd–even oscillation is symmetric, indicating that the orientation of the terminal moiety is the main contributor to the Gibbsian surface energy, suggesting insignificant changes in the surface entropy (distribution of the orientation state of the terminal moiety). Therefore, we infer that there are four main phases in SAMs: (1) the pseudoformed/substrate bonding dominated phase (≤C₃ SAMs), (2) the gauche defect dominated liquid-like phase (C₄–C_8/9 SAMs), (3) the transitional waxlike phase (C_9/10–C₁₃), and (4) the well-ordered solid-like phase (≥C₁₄ SAMs). These observations, therefore, should inform recent works using SAMs that compare properties across all length cases, while supporting recently developed theories in understanding discrepancies across earlier works in SAM characterization.
• (v)Simplicity, and thermodynamics, as manifested in sessile drop wetting is an ample tool to delineate complex interfacial properties. In this, and preceding papers, we demonstrated that by felicitous choice of probe liquids and experimental variables, properties of an otherwise complex system can be delineated through physical-organic studies. We demonstrate that wetting and associated interfacial energy relations are a powerful and reliable tool in the study of surfaces and, with appropriate measures, can generate complex information as obtained by advanced tools like sum-frequency-generation spectroscopy. By introducing the “gauche-defect density”-correlated dimensionless parameter, χ_c, we provide a direct empirical route to evaluate SAM quality without the need for advanced tools.

Experimental Analysis

Chemicals and Materials

Alkanethiol reagents were purchased from Sigma-Aldrich. Ethanol, 200 proof, was purchased from Decon Laboratories, Inc. All chemicals and reagents were used as received. Nitrogen and argon gas were purchased from Airgas and used as supplied.

Substrate Preparation and Characterization

Both Ag and Au (99.99%) films were evaporated in a Temescal BJD-1800 e-beam evaporator. Au and Ag films of 200 nm were evaporated onto 3 in. silicon wafers. Afterward, template stripping was performed to obtain the ultraflat surfaces, as previously reported.^21,23,32,46 In general, glass pieces, on which 8 μL of the optical adhesive (Norland Optical Adhesive 61) was applied, were place on top of a metal film. After 12 h of UV light curing, the glass with the metal film glued to it was stripped from the silicon wafer using a razor blade. Surface characterization details (AFM, SEM, and XRD) are available in the SI.

Preparation of Monolayers

Freshly template-stripped Ag^TS and Au^TS were cleaned with ethanol and dried with nitrogen gas. As previously reported,^4,22,23,32 SAMs were prepared by placing the template-stripped metal surface into a vial containing 3 mmol alkanethiol in 5 mL of 200 proof ethanol. The surface and thiol solution were incubated for at least 3 h under an inert atmosphere. The SAM was rinsed with copious ethanol and dried with a stream of nitrogen gas.

Measuring the Contact Angle

Static contact angles formed between the SAMs and probe liquids, deionized water, and HD were measured using the Ramé-Hart Goniometer (model 100-00) with a tilting base. A droplet of the probe liquid (1.0 μL) was dispensed onto the SAMs through an integrated syringe pump. Images of the droplets generated on SAMs were analyzed with the DropImage software.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b00355.

• Additional experimental section, results, and analysis (PDF)

The authors declare no competing financial interest.