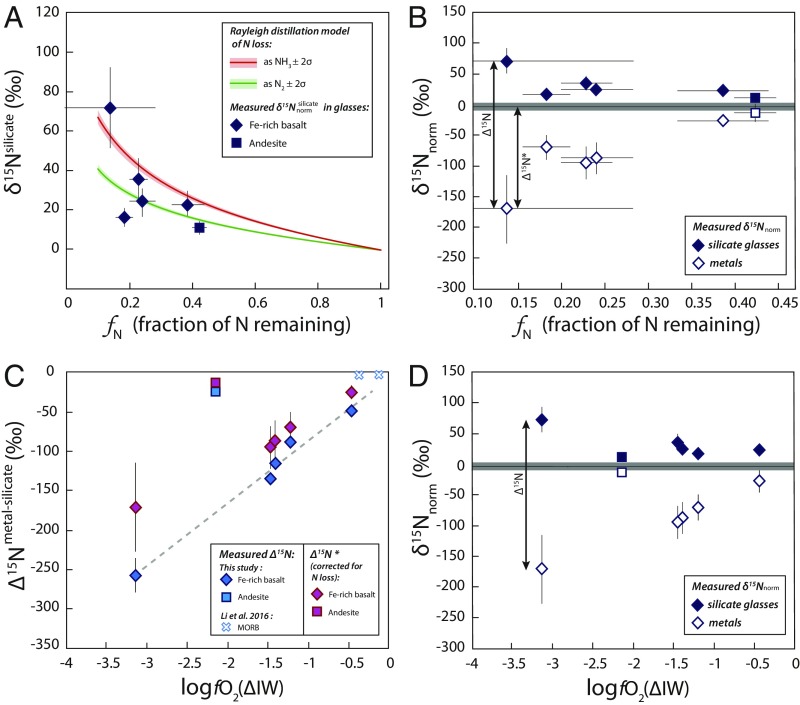
Fig. 3.

Effect of N loss (A and B) and fO₂ (C and D) on N-isotopic fractionation ∆¹⁵N^{metal-silicate}. (A) Modeled effect of N loss by Rayleigh distillation on the δ¹⁵N_norm values of silicate glasses as a function of f_N, the fraction of N remaining in the sample at the end of the experiments compared with the initial N content of the starting materials. The ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ values represent measured ¹⁵N/¹⁴N^silicate ratios normalized to the initial ¹⁵N/¹⁴N ratio of the starting material (see text and Table 1). Rayleigh distillation was modeled for N₂ loss (green curve) and NH₃ loss (red curve) as ${\text{δ}}^{15}{\text{N}}^{\text{silicate}}=\mathrm{1,000}\cdot \left(f_{\text{N}}^{\left(\left(1/\alpha \right)-1\right)}-1\right)$, where α is the fractionation factor approximated here by $\sqrt{\left[m\left({}^{15}\text{N}\right)+m\left({}^{14}\text{N}\right)\right]/m\left({}^{14}\text{N}_2\right)}$ = 1.02 for N₂ loss and by $\sqrt{\left[m\left({}^{15}\text{N}\right)+3\cdot m\left(\text{H}\right)\right]/\left[m\left({}^{14}\text{N}\right)+3\cdot m\left(\text{H}\right)\right]}$ = 1.03 for NH₃ loss. The positive δ¹⁵N values measured in our silicate glasses can be explained by the Rayleigh distillation model, suggesting that N loss may have increased the δ¹⁵N values of the silicate glasses. (B) Evolution of δ¹⁵N in the silicate glasses (closed symbols) and in the metal blobs (open symbols) as a function of f_N. The δ¹⁵N_norm values represent measured ¹⁵N/¹⁴N^p ratios (p representing the metallic or silicate phase) normalized to the initial ¹⁵N/¹⁴N ratio of the starting material (see text and Table 1), and the gray line at 0‰ represents the initial δ¹⁵N_norm value. The difference between the δ¹⁵N values measured in the metal and the silicate phases (δ¹⁵N^metal − δ¹⁵N^silicate) approximates the calculated ∆¹⁵N^{metal-silicate} values. Considering that positive ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ values may have been produced by N loss, the difference between the initial ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}$ (0‰) and the ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{metal}}$ values corresponds to ∆¹⁵N*, the N-isotopic fractionation corrected for N loss. (C) ∆¹⁵N^{metal-silicate} as a function of fO₂, showing both calculated ∆¹⁵N^{metal-silicate} (blue symbols) and ∆¹⁵N* (purple symbols). The small blue x's are reproduced from Li et al. (16), with fO₂ values recalculated following the procedure described in the text. Error bars represent 2σ SDs. Whereas the uncertainties on ∆¹⁵N^{metal-silicate} are determined from the SDs on ¹⁵N/¹⁴N ratios measured by SIMS, the larger uncertainties on f_N, δ¹⁵N_norm values, and ∆¹⁵N* are derived from the weighing uncertainties associated with the addition of Si₃¹⁴N₄ and Si₃¹⁵N₄ to the starting materials. The dashed line represents a linear regression (r² > 0.9) on the ∆¹⁵N^{metal-silicate} values measured in Fe-rich basalt. ∆¹⁵N^{metal-silicate} data describe 2 trends that can be explained by compositionally dependent differences in N speciation in the silicate glasses (see text). (D) Evolution of δ¹⁵N_norm in the silicate glasses and metal blobs as a function of fO₂. This plot shows that positive ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ values can also be produced by N-isotopic fractionation during metal segregation from the melt via the formation of ¹⁴N–Fe bonds in the metal from ¹⁴N in NH complexes in the melt. This process becomes more important as the fO₂ decreases due to the increasing stabilization of NH complexes in the melt under more reducing conditions.