Axonal Anatomy Optimizes Spatial Encoding in the Rat Entorhinal-Dentate System: A Computational Study

Abstract

Objective:

The network architecture connecting neural regions is defined by the organization and anatomical properties of the projecting axons, but its contributions to neural encoding and system function are difficult to study experimentally.

Methods:

Using a large-scale, spiking neuronal network model of rat dentate gyrus, the role of the anatomy of the entorhinal-dentate axonal projection was evaluated in the context of spatial encoding by incorporating grid cell activity to provide physiological, spatially-correlated input. The dorso-ventral extents of the entorhinal axon terminal fields were varied to generate different feedforward architectures, and the resulting spatial representations and spatial information scores of the network were evaluated. Position was decoded from the population activity using a point process filter to investigate the contributions of network architecture on spatial encoding.

Results:

The model predicted the emergence of anatomical gradients within the dentate gyrus for place field size and spatial information along its dorso-ventral axis which were dependent on the extents of the entorhinal axon terminal fields. The decoding results revealed an optimal performance at an axon terminal field extent of 2 mm which lies within the biological range.

Conclusion:

The axonal anatomy mediates a trade-off between encoding multiple place field sizes or achieving a high spatial information score, and the combination of both properties is necessary to maximize spatial encoding by a network.

Significance:

In total, this work establishes a mechanistic neuronal network model that, in concert with information-theoretic and statistical methods, can be used to investigate how lower-level properties contribute to higher-level function.

I. Introduction

The function of the hippocampus is strongly implicated in the formation of episodic memory [1]–[3]. The basis of such a function must arise from the collective properties of the neural components within the hippocampal system and their interactions. Such properties include the network/circuit architecture, the neuron morphology, their biophysical properties, synaptic dynamics, and synaptic plasticity. Therefore, by using the vast amounts of quantitative data available on the hippocampus to constrain and represent these properties in a computational model, a computational approximation of the hippocampus and its functions can be simulated. We are developing a platform from which a full-scale, biologically realistic, spiking neuronal network model of the entorhinal-dentate system of the rat hippocampus was constructed. The model represents one complete dentate gyrus including one million compartmental models of granule cells with realistic dendritic morphologies and over 3 billion perforant path synapses [4].

Our previous work with this model used random synaptic inputs to characterize its baseline activity. We found a strong role for topography in determining hippocampal system dynamics, as has been observed in theoretical models of other brain regions [5]-[8]. Topography refers to the ordered anatomical arrangement of axonal projections, originating from a presynaptic population and synapsing onto a postsynaptic population, that results in a system-level connectivity which may impose an organization to the information being transmitted. Such an organization has been characterized for the entorhinal-dentate projection by Dolorfo and Amaral [9], and this data was quantified for use in the network connectivity for our model [4]. The anatomical distribution of information then may represent a foundational “bias” that the neural system must then incorporate into its response. However, the random nature of the input in the previous work, though useful in characterizing the dynamical properties, precluded an analysis relating topography, or other model parameters, to higher level functions of the system. Therefore, physiological inputs were sought to allow the activity of the model to be interpreted with respect to higher level function.

Grid cells of the medial entorhinal cortex (MEC) encode information about position, expressing spatial receptive fields in a grid-like pattern that span the environment that an animal explores [10]. They represent a large portion of the inputs to the hippocampus and are necessary for the formation of place cells within the hippocampus [11]–[15]. Thus, grid cells and place cells are important as they provide the spatial context for memory events [16]. Measurement of various properties of the grid cells in rat have revealed that the size of the spatial receptive fields, i.e., the grid fields, varies among grid cells following an anatomical gradient [10], [17], [18].

Using the spatially-correlated activity provided by grid cells to drive a large-scale, mechanistic, spiking neuronal network model of the rat entorhinal-dentate system which included120,000 granule cells and 5,600 basket cells, the influence of topography on a network’s ability to encode spatial information was investigated. The size of the axon terminal field of the entorhinal-dentate projection was varied to explore how different feedforward architectures affected network dynamics, spatial representation, i.e., place field properties, and neuronal spatial information. A point process filter based on the work of Brown et al., 1998 [19] was used to assess the ability of the different feedforward architectures to encode spatial information and quantify it at the network level. Using these methods, we explore the role of network architecture on the neural encoding of spatial information.

II. Materials & Methods

The large-scale model simulations described here were designed to be analogous to typical in vivo experiments for determining place fields. In such experiments, a rat explores an environment during which neuronal spiking activity is recorded. The distribution of spikes is plotted against the location of the rat to identify regions in space where the neuron prefers to fire. Ideally, a rat will randomly and uniformly sample its entire environment for a sufficient time to allow the conditional firing probability as a function of x- and y-position to be calculated for each neuron. A random sampling is ideal to eliminate correlations that would arise based on patterned movements, and a uniform sampling is ideal to ensure that sufficient numbers of samples are obtained equally across all possible locations within the environment.

For computational simulations, a random path model was used to mimic the movement of a rat in a fixed environment. Experimentally, recordings are often performed during sessions that range from 20 minutes to one hour [15], [20], [21]. However, the computational complexity of the large-scale model had previously limited simulation times to 10 seconds. In order to complete 20 minute simulations in a reasonable amount of computational time, the complex neuron morphologies were simplified using an equivalent circuit algorithm developed by Marasco et al., 2012 [22].

The methods section will first describe the large-scale model and the equivalent circuit algorithm. It will then describe the methods for generating realistic grid cell activity, the procedure for extracting and characterizing place fields, and the statistical methods used to decode position and quantify information at the network level.

A. Large-Scale Model

Neuron models were constructed and simulated using the NEURON simulation environment [23]. Granule cells were represented using a multi-compartment model with the electrophysical properties of each compartment being modeled by an electrical circuit. The reduced granule cell models consisted of four compartments corresponding to the soma and the dendrites in the inner, middle, and outer thirds of the molecular layer. The parameters of the reduced model were obtained by creating an equivalent circuit model based on the complex morphology (see [22]). Compartments in series and parallel could be combined using standard circuit approaches to create a reduced model that preserved the electrophysiological properties characteristic of granule cells (Table 1). The channel conductances can be found in the Supplementary Materials. Basket cells were represented using a single compartment model with properties obtained from [24]. Gaarskjaer [25] measured the dimensions of an unfolded rat dentate gyrus and reported a septo-temporal length of 10 mm. Neurons were instantiated in a dentate gyrus map following those dimensions. synaptic connections between neurons were simulated using a distance-based rule that followed anatomically derived constraints. Axons were functionally represented as time delays that were computed based on the axonal path length distance between the soma at which the action potential was initiated and the receiving postsynaptic neuron using an action potential propagation velocity of 0.32 mm/ms [26]. The entorhinaldentate projection was mapped based on a comprehensive study that used a series of retrograde tracers injected into the dentate gyrus [9]. Quantification of the data is described in [4]. Connectivity was stochastically generated by converting spatial axon density data into distance-based Gaussian probabilities for entorhinal cortical, granule, and basket cells. Convergence values were estimated using dendritic lengths, spine density counts, and presynaptic-postsynaptic population ratios (see [4]). Basket cells provided both feedforward and feedback inhibition to granule cells (see [27]). Entorhinal input to basket cells provided a basis for feedforward inhibition, and granule cell input to the basket cells activated feedback inhibition. Suprapyramidal granule cells received 2117 grid cell inputs and 2417 LEC inputs. Infrapyramidal granule cells received 1253 grid cell inputs and 1479 LEC inputs. These numbers were derived from morphological and spine density data (see [4]) which report that suprapyramidal granule cells had a larger total dendritic length [28] and higher spine densities than infrapyramidal granule cells [29], [30]. Suprapyramidal and infrapyramidal granule cells received 108 and 68 basket cell inputs, respectively. Each basket cell received 871 MEC inputs, 1161 LEC inputs, and 915 granule cells. The conductance time course of synapses upon activation was modeled using two exponentials [24], [31] with parameters optimized to match excitatory and inhibitory postsynaptic potential data for the respective synapses. The excitatory conductances represented AMPA receptors, and the inhibitory conductances represented GABA_A receptors.

TABLE I.

Electrophysiological properties of the reduced granule cell model

Electrophysiological Property	Original Model	Reduced Model	Biological Value	General Description of Calculation
RMP (mV)	−73.5	−73.5	−75 ± 2a	The somatic membrane voltage at rest was measured.
			−74.7 ± 0.9b
RIn (MΩ)	169	170	228 ± 14.2c	A series of step currents of different amplitudes were applied to the soma and the slope of the steady-state voltage change per current amplitude was calculated.
			122 ± 13b
τmembrane (ms)	24.5	24.9	31 ± 2a	The repolarization of the somatic membrane voltage following a depolarizing current was fitted to an exponential function.
			16 ± 1b
AP Threshold (mV)	−50.4	−50.4	−49 ± 0.8c	The minimum voltage at which an action potential can be elicited was determined.
			−40.8 ± 0.6b
Fast AHP (mV)	−6.34	−2.88	−11.7 ± 1.1a	The difference between the peak AHP amplitude and the resting membrane potential after the firing of an action potential was measured.
			−7.6 ± 0.6b
Spike Frequency Adaptation Ratio	0.087 or 0.34	0.52 or 0.55	0.092 or 0.3c	The property was calculated as the ratio between (1) the initial inter-spike interval (ISI) and the final ISI or (2) the mean of the first two and last two ISIs.
Sag Ratio	1	1	0.97 ± 0.01a	The ratio was determined using the steady-state membrane voltage change following a hyperpolarizing current and the maximum change.
			1.0 ± 0.2b

Values report mean and standard deviation where applicable.

References:

^aLübke et al., 1998 [27];

^bKowalski et al., 2016 [28];

^cStaley et al., 1992 [29].

B. Grid Cell Activity

Blair et al., 2007 [32] developed a mathematical description to model grid maps involving the summation of three cosines that are rotated in increments of 60° to form the characteristic triangular lattice pattern of grid maps

$$G(r,\lambda ,\theta ,c)=g\left({\sum }_{k=1}^3\text{cos}\left(\frac{4\pi }{\sqrt{3\lambda }}u\left({\theta }_k+\theta \right)\cdot (r-c)\right)\right),$$ (1)

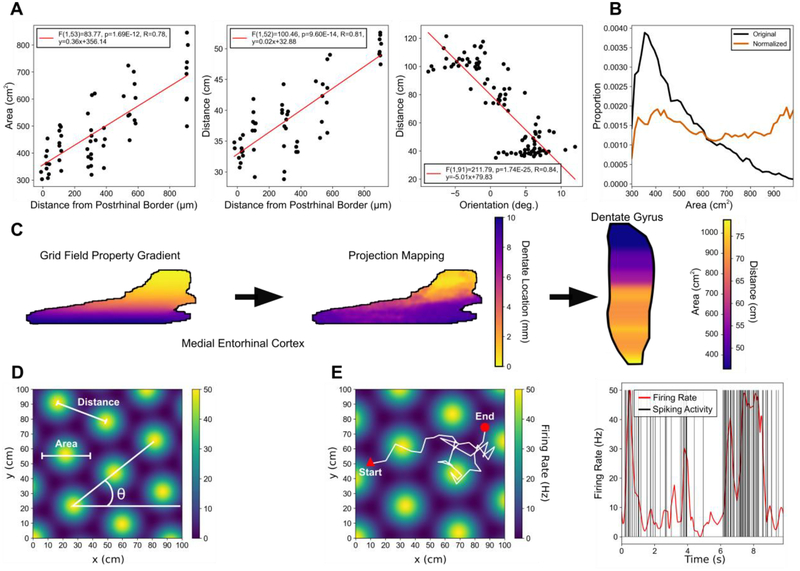
where the function u(θ_k + θ) = (cos(θ_k + θ) , sin(θ_k + θ)) determines the relative and global rotation of the cosines. The vector r corresponds to the position (x,y) with c = (x₀,y₀) determining the spatial offset of the grid map, and the variable λ sets the distance between the grid fields. The function g(x) = e^a(x-b) − 1 was chosen to act as a monotonically increasing gain function where the parameter a determines the width of the place fields, and b = −3/2 is used to set the minimum value of the function to zero. The grid maps then were normalized such that the peak firing rate was 50 Hz. Figure 1D summarizes the major properties of grid maps.

Fig. 1.

Distribution of grid field parameters and generation of grid cell activity. (A) Data from Hafting et al., 2005 (left and middle) and Stensola et al., 2012 (right) were used to constrain the grid field properties. (B) The grid field properties were normalized along the dorso-ventral axis of the medial entorhinal cortex using a generalized logisitic function such that the grid field properties were represented approximately equally. (C) The gradient of grid field parameters in the medial entorhinal cortex (left) and the mapping between medial entorhinal cortex and dentate gyrus (center) determine where the grid field information is communicated to within the dentate gyrus. The final distribution of grid field parameters results in a gradient in the dentate gyrus (right). (D) An example grid field is shown with notation describing the field area, distance, and orientation properties. (E) Left: The movement of a virtual rat in white is overlaid on a grid field with a triangle and circle denoting the start and end points of the movement, respectively. Right: The firing rate (red) is determined using a grid field and the movement of the rat through the field. A non-homogeneous Poisson process is used to generate spiking activity (black) using the firing rate.

The position of a virtual rat as it explored an 80 cm by 80 cm square environment was used as an input to the above function to obtain a position-dependent, time-varying firing rate. Movement was modeled by sampling from uniform random distributions that defined the speed of the rat (0–30 cm/s), the direction of movement (0°–360°), and the period of time during which the rat would move with the sampled velocity vector (0–500 ms). If the trajectory of the rat would take it beyond the boundaries of the environment, the rat’s movement would be reflected by off the boundary.

The resulting firing rate was used as input to an inhomogeneous Poisson renewal process to generate spike times (Fig. 1E). When a spike was elicited by a Poisson process, the firing rate after the spike time would be modified by a refractory period with an exponential time course having a time constant of 35 ms, preventing inter-spike intervals from becoming too short. The time constant was estimated from data published by Alonso and Klink 1993 [33].

The parameters of the grid maps were constrained based on the supplementary data published by Hafting et al., 2005 [10] (Fig. 1A). They reported a linear relationship between both the grid spacing and the grid field area and the entorhinal distance from the postrhinal border which corresponds approximately with the dorso-ventral position within the MEC. Stensola et al., 2012 [18] further reported a linear relationship between grid spacing and grid orientation. Linear regressions between the grid field properties and MEC dorso-ventral position were performed to quantify the anatomical organization of grid field properties.

A uniform distribution for grid field sizes and grid spacing was assumed for the model such that each grid field size was equally represented. Uniform distributions were constructed by transforming the grid map gradient with a sigmoidal function which was based on the distribution of grid cells within the MEC (Fig. 1B) following

$$y(x)=A+\frac{K-A}{{\left(1+e^{-B(x-M)}\right)}^{(1/v)}},$$ (2)

where y(x) represents the grid field size at a given dorsoventral position, A = 0.3256, K = 2.4239, B = 2.15, M = −1.7858, and v = 0.01.

C. Place Field Calculation

An initial rate map was created by discretizing the environment explored by the virtual rat into bins of size 2 cm by 2 cm. The number of spikes that were elicited by a granule cell in each bin was counted and divided by the amount of time spent in each bin. The rate maps then were smoothed using a modified version of the adaptive smoothing procedure described by Skaggs et al., 1996 [34]. The original procedure expanded a circle around each bin and used a criterion based on a meta parameter and the number of samples available within the circle to determine the size of the circle, i.e., the extent of the smoothing. The circle weighted all bins equally. The modified procedure weighted each bin based on the distance from the center using a Gaussian function. The standard deviation of the Gaussian function was increased until the weighted number of samples satisfied the criterion set by the same meta parameter using the following equation:

$$N_{spikes}>\frac{\alpha }{N_{occ}^2{\sigma }^2},$$ (3)

where N_spikes corresponds to the number of spikes transformed by the Gaussian function, N_occ is the number of samples transformed by the Gaussian function, σ is the standard deviation of the Gaussian, and a is the meta parameter that controls the amount of smoothing, set at 1.0 × 10¹³.

A grid-based version of the density clustering algorithm, DENCLUE, was used to quantify the number of place fields and areas of the place fields of the smoothed rate maps. The original DENCLUE algorithm smooths the data using a density kernel and uses a local hill climbing procedure to identify data points that share the same local maxima as clusters [35]. A grid-based version was developed to reduce the number of data points that needed to be clustered and increase the speed of the algorithm. The density kernel was a Gaussian function that used the standard deviations that satisfied the sampling criterion during the adaptive smoothing procedure. Clusters were subjected to a threshold such that bins less than 40% of the maximum value of the cluster were removed. Processed clusters with an area less than 200 cm², as described by Muller and Kubie, 1989 [36], were not considered to be clusters.

D. Spatial Information Score

The spatial information score was calculated using a histogram-based method proposed by Skaggs et al., 1996 [34] with

$$SI={\sum }_{i=1}^N{p}_i\frac{R_i}{R}lo{g}_2\frac{R_i}{R},$$ (4)

where the environment was divided into non-overlapping bins indexed by i = 1, … ,N, p_i. is the probability that the rat is in bin i, R_i is the mean firing rate for bin i, and R is the overall mean firing rate. The metric is called spatial information score in this work to differentiate it from information as it is defined by information theory. The spatial information score resembles the calculation of the mutual information but does not follow the exact form in terms of joint and marginal probabilities.

E. Recursive Point Process Filter for Decoding

Brown et al., 1998 [37] developed a statistically-based, recursive point process filtering technique that could use the receptive field and spiking activity of one or more neurons to estimate the quantity that was being encoded. The same technique was applied to estimate the position of the rat using the following equations:

One-Step Prediction

$$x_{k|k-1}=x_{k-1|k-1}+F{x}_{k-1|k-1}$$ (5)

One-Step Prediction Variance

$$W_{k|k-1}=F{W}_{k-1|k-1}{F}^T+R{W}_{\epsilon }$$ (6)

Posterior Variance

$$W_{k|k}{}^{-1}=W_{k|k-1}{}^{-1}+{\sum }_{c=1}^C\left[\left[\nabla \text{log}\left({\lambda }_{k\mathrm{\Delta }}^c\right){\left[{\lambda }_{k\mathrm{\Delta }}^c\mathrm{\Delta }\right]}^T\right]-{\nabla }^2\text{log}\left({\lambda }_{k\mathrm{\Delta }}^c\right)\left[n_{k\mathrm{\Delta }}^c-{\lambda }_{k\mathrm{\Delta }}^c\mathrm{\Delta }\right]\right]$$ (7)

Posterior Mode

$$x_{k|k}=x_{k|k-1}+W_{k|k-1}{\sum }_{c=1}^C\nabla \text{log}\left({\lambda }_{k\mathrm{\Delta }}^c\right)\left[n_{k\mathrm{\Delta }}^c-{\lambda }_{k\mathrm{\Delta }}^c\mathrm{\Delta }\right]$$ (8)

The temporal spiking activity for each neuron was discretized into bins such that a one signifies that an action potential was generated and a zero signifies no action potential. The bins were indexed by the variable k which denotes the bin number, and Δ defines the bin size which was 1 ms.

The variable ${\lambda }_{k\mathrm{\Delta }}^c$ indicates the firing rate for the neuron indexed by the variable c and at time kΔ. The generation of an action potential at time kΔ is denoted by $n_{k\mathrm{\Delta }}^c$ Thus, the probability of firing an action potential is determined by multiplying the firing rate with the bin size, ${\lambda }_{k\mathrm{\Delta }}^c\mathrm{\Delta }$. The ∇ and ∇² variables represent functions for the first and second derivatives with respect to position.

The state evolution matrix F and covariance matrix W_ε were calculated by calculating a first-order autoregressive model of the path of the rat. During One-Step Prediction, the position x_k|k−1, is estimated using the autoregressive model parameters and the previous position estimate x_k−1|k−1, which incorporates the spiking history within the interval (0, (k-1)Δ). Similarly, One-Step Prediction Variance estimates the covariance matrix of the One-Step Prediction position based on the autoregressive model parameters and the previous covariance matrix estimate.

The Posterior Mode and Variance use the neuron firing probabilities and the spiking activity at time kΔ to update the one-step estimates and obtain the estimate of the current position, x_k|k, and the covariance matrix of the posterior, W_k|k, under the assumption that the neurons are conditionally independent. These estimates incorporate the spiking history within the interval (0, kΔ). The derivatives of the log of the firing rates are weighted by the firing probabilities and spike counts to compute these estimates. The derivation of equations (4–7) are detailed by Barbieri et al., 2004 [38].

To facilitate the computation of the first and second derivatives of the rate maps during the decoding process, the rate maps were represented by a set of Legendre polynomials which are differentiable and form an orthonormal basis within the interval [-1,1] [39]. Their equations are presented in the Supplementary Materials.

F. Lower Bound of Mutual Information Encoded by Network

Pillow et al., 2000 [40] derived a generalized estimate for the lower bound of the mutual information and was used in the present study as an information-theoretic measure to characterize the ability of the network to encode position. A brief derivation is located in the Supplementary Materials.

$$I[x;r]\ge \frac{1}{2}\left[{\text{log}}_2\left[{(2\pi e)}^2\left|W_{\epsilon }\right|\right]-\left({\text{log}}_2\left|E\left[r\cdot r^T\right]\right|+{\text{log}}_2(2\pi e)\right)\right]$$ (9)

Here, W_ε refers to the covariance matrix in (6), and E [r · r^T] corresponds to the covariance of the residuals where $\widehat{x}$ or the error of the estimate.

III. Results

A. Emergence of Place Fields

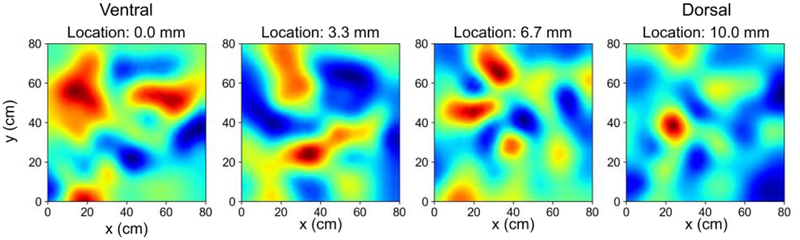
The network was driven by input from both the medial and lateral entorhinal cortices. The MEC provided spatially-correlated grid cell input, and the LEC provided spatially-uncorrelated input as random, Poisson activity, contributing noise to the grid cell input. Entorhinal-dentate system simulations were performed using experimentally-derived constraints for all aspects of the model (e.g., cellular biophysics, convergence, divergence, EPSP/IPSP parameters, grid cell receptive field properties, etc.). Each simulation represented 2,000 seconds which took 98 hours per simulation using 1,000 processors. Simulation results revealed that under these conditions granule cell activity exhibited multiple, irregularly spaced place fields which matched experimental descriptions of granule cell place fields (Fig. 2) [41], [42]. Experimental studies reported an average of 2.2 place fields with an area of 667.3 cm² [11], [42]. The average number of place fields per granule cell from simulation was 4.10 ± 1.66, and the average area was 719.5 ± 185.6 cm². Neunuebel and Knierim, 2012 [21] had reported an average spatial information score of 1.1 ± 0.56 bits/spike for experimentally recorded granule cells, and the simulations reported here resulted in an average spatial information of 0.83 ± 0.03 bits/spike. The quantitative similarities between the simulated and experimental place fields demonstrate that the large-scale model, in addition to accurately representing cellular dynamics, can adequately recreate phenomena at a higher level involving network dynamics essential for spatial cognition.

Fig. 2.

Smoothed rate maps from simulated dentate granule cells at different locations along the dorso-ventral axis. A dorso-ventral gradient for the size of the place fields was observed. Ventrally-located granule cells exhibited larger place fields, and dorsally-located granule cells exhibited smaller place fields. The color scale denotes high firing rates in red and low firing rates in blue.

B. Evaluating Gradients in Dentate Gyrus

The gradient of grid map properties within the MEC and the gradient of entorhinal-dentate projections align such that grid cells associated with smaller place fields are transmitted along projections terminating within the dorsal dentate gyrus, while grid cells associated with larger place fields are transmitted along projections terminating within the ventral dentate gyrus (Fig. 1C). This relation suggested that the dentate gyrus would exhibit place field properties such that granule cells within the dorsal dentate gyrus would express smaller place fields and granule cells within the ventral dentate gyrus would express larger place fields. Therefore, an analysis was performed to quantify the emergence of any possible gradient in the place field properties of granule cells with respect to dorso-ventral position.

A second gradient was hypothesized to emerge along the transverse axis due to the difference in number of inputs the suprapyramidal and infrapyramidal blades received, so the data was further divided into suprapyramidal and infrapyramidal populations. Therefore, the subsequent analyses investigated the presence and magnitude of the dorso-ventral gradients that occurred in the suprapyramidal and infrapyramidal blades.

C. Place Field Area Gradient Depends on Axonal Anatomy

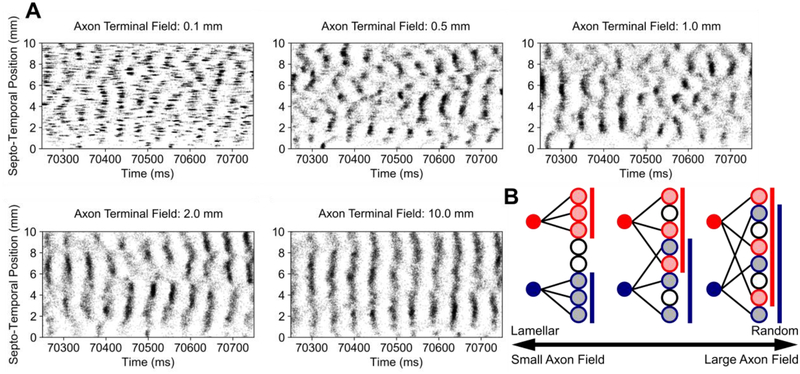
A linear regression was performed between the mean place field area and dorso-ventral position, and a gradient was discovered in which smaller place fields were generated dorsally and larger place fields were generated ventrally. To test the influence of topography on the emergence of place field area gradients, the dorso-ventral extent of the axon terminal fields of the entorhinal projection were varied in a log-linear manner, i.e., 0.1 mm, 0.5 mm, 1.0 mm, 2.0 mm, and 10.0 mm, due to the computational resources necessary to complete a single simulation. The extent of the axon terminal field constrains the area in the dentate gyrus to which a single entorhinal neuron could form synaptic connections and was used as a continuous quantity through which the entorhinal-dentate connectivity could be transitioned between a lamellar connectivity and a uniform random connectivity (Fig. 3B). The spatio-temporal activity due to different axon terminal field extents and a conceptual representation of the axon terminal field are depicted in Fig. 3A. As previously reported in [4], the axon terminal field controls the spatial extent of the clusters.

Fig. 3.

Raster plots of the spiking activity due to different axon terminal field extents. (A) Spiking activity is represented using black dots which represent the time and position along the longitudinal extent at which an action potential was generated. Clustered activity is apparent with smaller axon terminal field sizes and organizes into vertical bands at larger axon terminal field sizes. (B) A conceptual representation of the consequences of changing the axon terminal field have on connectivity is depicted. As the axon terminal field grows larger, a larger area of neurons can be contacted, and the input is more dispersed spatially. At smaller axon terminal fields, the area in which neurons can be contacted becomes restricted.

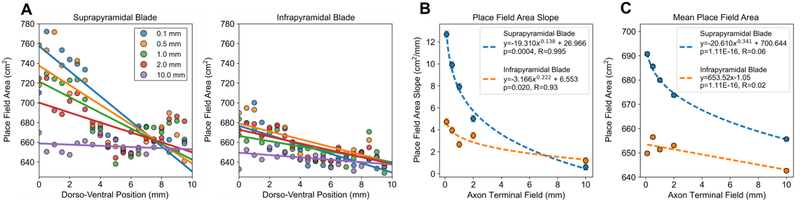
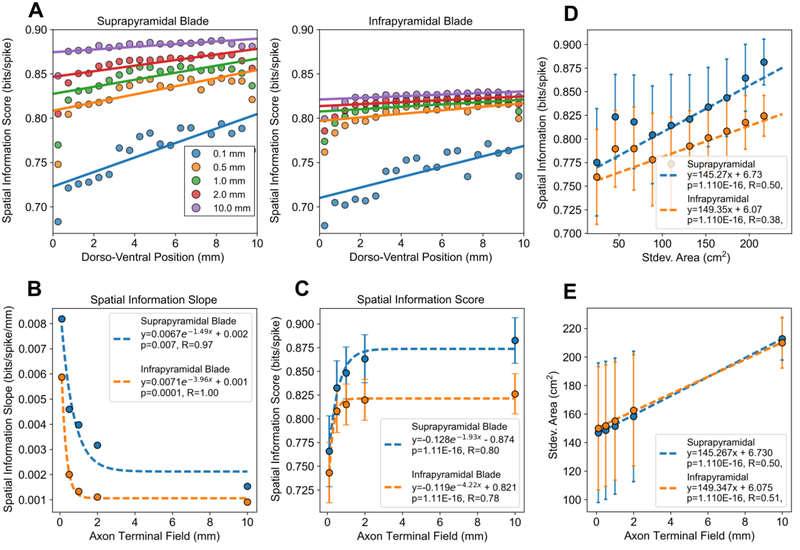
Shorter axon terminal field extents resulted in a linear decrease in place field area along the dorso-ventral axis (Fig. 4A). The slope was used as a measure to quantify the range of place field sizes, i.e., spatial resolutions, that the network represented. The slope decreased following a power law, i.e., log-linearly, as the axon terminal field extent increased (Fig. 4B). The mean place field area for the population was weakly correlated with the axon terminal field extent (Fig. 4C).

Fig. 4.

The effect of axon field terminal extent on granule cell place field properties and suprapyramidal-infrapyramidal differences. (A) The mean place field area within 0.5 mm bins along the dorso-ventral axis were plotted as a scatter plot with the corresponding linear fits. The mean values within a bin were plotted for visual clarity, but the regressions were performed using the raw data. (B) The magnitude of the slope between place field area and dorso-ventral position decreased log-linearly with the axon terminal field extent. The error bars denote the standard error of the estimates of slope. (C) The mean place field areas of the populations were weakly correlated with the axon terminal field extent. The error bars denote standard error. N_supra=65,000 and N_infra=55,000 for each field extent.

The place field area gradient was present in both the infrapyramidal and suprapyramidal populations with both populations exhibiting larger ventral place fields and smaller dorsal place fields. However, the suprapyramidal blade exhibited a steeper gradient. When comparing the mean place field areas between the infrapyramidal and suprapyramidal populations, the suprapyramidal granule cells had larger place fields regardless of the axon terminal field extent (p≪0.001 for all axon field extents).

There was no dorso-ventral gradient for the number of place fields generated per granule cell (data not shown). Suprapyramidal granule cells exhibited a slightly lower number of place fields (0.14 ± 0.03 place fields) though it was statistically significant (p ≪ 0.001 for all axon field extents).

D. Spatial Information Score Depends on Axonal Anatomy

A linear regression was performed between the spatial information score and dorso-ventral position which revealed that a spatial information gradient was present in the data for the dentate gyrus. The spatial information score was highest for the activity emerging from the dorsal dentate and was lowest for activity from the ventral dentate. Like the place field area gradient, the spatial information gradient approached zero as the topography became random (Fig. 5A and 5B). Contrary to the mean place field area which had a very weak correlation with axon field extent, the mean spatial information score for the population increased as the axon field extent increased (Fig. 5C). The 10 mm axon terminal field network had the highest spatial information score, whereas the 0.1 mm axon terminal field network had the lowest spatial information score.

Fig. 5.

The effect of axon terminal field extent on spatial information score and the effect of multi-resolution input on spatial information score. (A) The mean spatial information score within 0.1 mm bins along the dorso-ventral axis were plotted with the corresponding linear fits. The mean values within a bin were plotted for visual clarity, but the regressions were performed using the raw data. (B) The magnitude of the slope between the spatial information score and dorso-ventral position decreased exponentially with the axon terminal field extent. The error bars denote the standard error for the estimates for slope. (C) The mean spatial information increases exponentially with axon field extent. The error bars denote standard deviation. (D) The standard deviation of the grid field areas that a granule cell received were plotted against the corresponding spatial information score. (E) The standard deviation of grid field areas in the input is correlated with the axon terminal field extent. A larger axon terminal field results in a granule cell receiving a total input with a larger variety of grid field sizes.

The spatial information gradient was present in both the infrapyramidal and suprapyramidal blades, but the suprapyramidal blade displayed both a steeper spatial information gradient and a larger mean spatial information score than the infrapyramidal blade (p≪0.001 for all axon field extents).

E. Multi-Resolution Inputs Affect Spatial Information Score

We next investigated the mechanism by which axon terminal field contributed to the spatial information score. Theoretical studies have concluded that a multi-resolution representation of space in the input is important to generate singular place fields [14], [43]. We hypothesized that wider axon terminal fields would result in granule cells receiving inputs composed of a larger variety of grid field sizes which would cause the granule cells to exhibit a higher spatial information score. To test this hypothesis, a linear regression was performed between the spatial information score and the amount of different spatial resolutions, i.e., grid field sizes, represented by the total input to a granule cell which demonstrated that the spatial information score is improved by a multi-resolution input (Fig. 5D). The amount of different resolutions encoded by the input was quantified by calculating the standard deviation of the grid field areas that comprised the inputs to a granule cell. Additionally, the amount of different spatial resolutions received by granule cells was correlated with the extent of the axon terminal fields as the axon fields constrained the divergence of the input within the postsynaptic region (Fig. 5E).

F. Spatial Information Score and Multi-Resolution Representations of Space Predict Decoding Performance

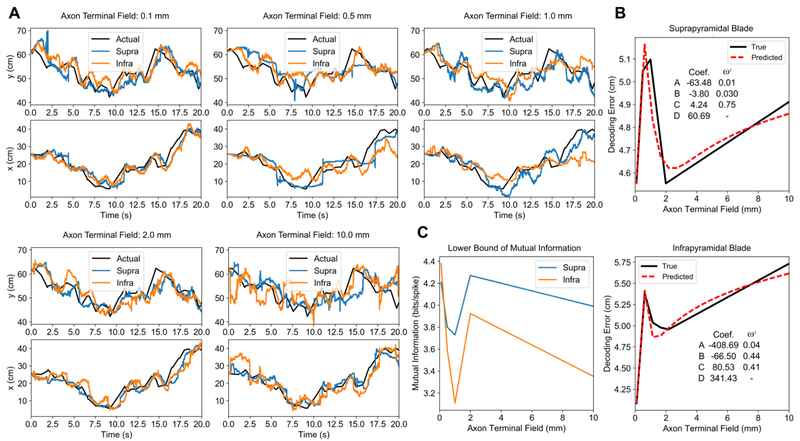
The next investigation evaluated position decoding performance using the activity generated by the neuronal network under the different axon terminal field conditions. A subset of 2000 neurons from the suprapyramidal blade and 2000 neurons from the infrapyramidal blade were chosen using a uniform random sampling along the longitudinal axis of the dentate gyrus. For each blade, decoding was performed using the same 2000 neurons for each axon terminal field extent. The position estimates and decoding performance are plotted in Fig. 6. Rather than a monotonic relation, decoding error varied nonlinearly as a function of axon terminal field extent. The smallest axon terminal field extent at 0.1 mm yielded the best estimate for both blades, followed by a large increase in error at 0.5 mm, a local minimum at 2.0 mm, and another increase in error at10.0 mm (Fig. 6B). The lower bound of spatial information was found to vary with the decoding error (Fig. 6C). To explore the relation between axon terminal field size and decoding error, we performed an analysis using the results obtained in the previous sections. We had demonstrated two opposing gradients: the range of place field areas that are represented by the population decreased as the axon field increased, but the spatial information score increased as the axon field increased. We hypothesized that, due to their opposing relations, decoding performance may be related to a combination of the two properties. The variables and their interaction were linearly combined using an equation of the form

$$\widehat{E}(x)=A\cdot f_{SI}(x)+B\cdot f_G(x)+C\cdot f_{SI}(x)\cdot f_G(x)+D,$$ (10)

where $\widehat{E}$ refers to the predicted decoding error, x refers to the axon terminal field extent, f_G (x) refers to power law equations for place field size gradient from Fig. 4B, and f_SI(x) corresponds to the power law equations for spatial information score from Fig. 5C. The power law equations were also used to interpolate additional points along the predicted decoding performance curve. The effect size of each variable was quantified using ω² which indicated that the interaction between spatial information score and slope was a significant predictor of decoding error (Fig. 6B). These results suggest that a combination of a multi-resolution input and the spatial information score contributes to optimal spatial encoding. An interesting feature is the local minimum in the actual decoding error that appears at 2.0 mm for both blades and in the predicted decoding error at 2.43 mm and 1.32 mm for the suprapyramidal and infrapyramidal blades, respectively. These values are comparable to the anatomical axon field extents of 1–1.5 mm found in vivo [44].

Fig. 6.

Decoding performance as a function of axon terminal field extent. (A) The position decoding estimates under different axon terminal field conditions are plotted over the actual positions. (B) The average error, represented by the Euclidean distance between the predicted and actual position, is plotted against axon terminal field extent (black). A linear regression was used to predict decoding performance using two variables: place field area slope and spatial information score (red). The p-values of the regressions were ≪ 0.001 for both blades. The coefficients to Eq. 17 and the effect sizes are listed within each figure. (C) The estimated lower bound of the mutual information between position and the spiking of the neural population is plotted as a function of axon terminal field extent.

IV. Discussion

A. Large-Scale Modeling and the Incorporation of Biological Constraints

Perhaps the most significant finding of the present study is the successful prediction of place field properties of dentate granule cells in response to grid cell firing of entorhinal cortical neurons as inputs to the dentate. There was no information or constraint relative to place cell firing incorporated to any degree into the model. In this sense, then granule cell place fields truly represent a property that is emergent from the network. In addition to the simple emergence of place fields, the simulated entorhinal-dentate network also displayed multiple high-level properties of place fields displayed by granule cells in vivo [11]. For example, simulated granule cells exhibited an average of 4.10 ± 1.66 place fields with place field areas of 719.5 ± 185.6 cm2 which were comparable to the 2.2 place fields with areas of 667.3 cm2 that were measured in vivo [11], [42]. Furthermore, the average spatial information of the simulated granule cells was 0.83 ± 0.03 bits/spike which were within the experimentally reported values of 1.1 ± 0.56 bits/spike [21].

The only substantial constraints included in the model were morphological (e.g. the division of the apical dendrites of the granule cell models into the granule cell layer and the inner, middle, and outer thirds of the molecular layer and the numbers and densities of synapses), anatomical (e.g. the topographical projection of entorhinal axons to dentate gyrus and the numbers and distributions of neurons throughout the dentate gyrus), biophysical (e.g. the types and densities of the ion channels represented, see Supplementary Materials), and electrophysiological (e.g. the threshold, input resistance, spike frequency adaptation ratio, etc., see Table 1), and the synaptic dynamics.

Despite the number of components and interdependencies present in the model, the large-scale neuronal network was able to exhibit place field properties and spatial information scores that were within the ranges reported experimentally. Whereas synaptic and cellular dynamics represent a bottom-up or lower level validation and are the means by which neuronal network models are typically validated, the place fields and spatial information, which rely on a combination of multiple elements outside of the individual cell models, represent a top-down validation or validation at a higher level. Validation at both levels, given the number of components in the model, suggest that at least an appropriate number of significant components were included in the model to generate place field behavior and that these components were adequately constrained with respect to the biology.

B. Dorso-Ventral Gradient in Dentate Gyrus

A possible dorso-ventral organization in dentate gyrus due to the entorhinal-dentate topography and the organization of the grid cell receptive field properties had been proposed by Solstad et al., 2006 [14]. However, the quantification of data regarding the topography of the entorhinal-dentate projection and grid cell receptive field properties and the integration of both datasets into a comprehensive model had not been performed until this work. The large-scale model presented here predicts that the dentate gyrus has a functional, dorso-ventral organization in which smaller place fields are exhibited dorsally and larger place fields are exhibited ventrally. A similar gradient for place field area has been reported in vivo for the CA3/4 subfield [20] but has not been investigated for dentate gyrus. However, given that the entorhinal-CA3 projection is organized in the same manner as the entorhinal-dentate projection and that the dentate-CA3 projection has a strongly lamellar organization [45], [46], it is plausible that the prediction of the large-scale model is accurate.

C. Transverse Gradient in Dentate Gyrus

A transverse gradient was discovered between the suprapyramidal and infrapyramidal blades. Suprapyramidal granule cells exhibited larger place field areas, a greater place field area gradient, and higher spatial information scores than infrapyramidal granule cells. The key difference between the suprapyramidal and infrapyramidal granule cell models was the number of inputs that each received with 2117 and 1253, respectively. The ratio of grid cell to LEC inputs was similar with 43% and 46% of the inputs being composed of grid cells for suprapyramidal and infrapyramidal granule cells, respectively. The mean firing rates between the blades were similar at 0.70 Hz (suprapyramidal) and 0.68 Hz (infrapyramidal). Although the number of inputs were dissimilar, the feedback inhibition provided by basket cells caused the firing rates to be approximately equal. The range of spatial resolutions available for either the suprapyramidal or infrapyramidal granule cells in their input was also similar (Fig. 5E). This leaves the number of inputs as the main factor differentiating the two populations in the present model. A study investigating the differences between suprapyramidal and infrapyramidal granule cells may reveal additional insights as to the functional differences between the groups.

D. High-Level Constraints Predict Function of Lower-Levels

Controlling certain properties in neural systems experimentally (e.g. the size of the axon terminal field) can be impossible given current technology. Computational models, with sufficient detail to represent phenomena within and across different physical scales, can predict the role of lower level properties in a larger context. The axon terminal field was found to mediate a trade-off between encoding multiple spatial resolutions or achieving a high spatial information score. Beyond a highly multi-resolution representation of space as achieved by the 0.1 mm axon terminal field extent which resulted in the greatest decoding performance, the optimal axon terminal field extents to maximize spatial encoding was predicted to be 2.43 mm and 1.32 mm for the suprapyramidal and infrapyramidal blades which suggests that both properties are necessary for good encoding. Furthermore, these values lie within the range of the reported axon field extent for entorhinal cortical axonal fields within the dentate gyrus (roughly 1–1.5 mm by Tamamaki and Nojyo, 1993 [44]). These results suggest that spatial encoding efficiency may be one constraint that is used to determine the in vivo size of the entorhinal axon terminal field and demonstrate how the large-scale model can be used to generate hypotheses that connect lower level biological properties to a system level function.

In the context of quantifying high-level properties of neural system activity, information theory has been essential by providing a framework through which the non-linear relations between external, e.g., neural, biological, and behavioral, correlates and single neuron or ensemble neural spiking activity can be reduced into single number metrics. Statistical approaches including decoding algorithms and neural functional connectivity estimation methods can be used to extract various information-theoretic quantities directly from the spiking activity as opposed to histogram-based methods [38], [40], [47]. The lower bound of mutual information used in this study directly uses the error of the estimate to quantify mutual information, but using and developing more sophisticated techniques are necessary to provide accurate metrics for higher-level function.

E. Additional Contributions to Spatial Encoding

Though grid cells are an important physiological input to the hippocampus, there exist many other functional cell types in the entorhinal cortex that have not yet been incorporated which can add to the dimensions by which the large-scale model can be interpreted. Additional cell types from layer II of the MEC include boundary cells [48] and speed cells [49]. Deeper layers of the MEC have head direction cells and conjunctive cells [50]. Less is known about specific, functional cell types in the LEC and their topographic organization. Studies in rat have shown that the LEC responds to multi-modal sensory stimuli such as olfaction and vision [51], [52]. Additionally, there is evidence that LEC cells can encode locations of objects within an environment [53].

Basket cells in the model participated in both feedforward inhibition driven by the entorhinal cortex and feedback inhibition driven by the granule cells but a thorough investigation into their contributions on the processing of spatial information was outside the scope of this work. Feedback inhibition has been included in most computational studies of place field formation to provide competitive inhibition and promote sparse activity [11], [14], [54], but the influence of feedforward inhibition on place field formation has not been investigated in the literature. Future works will study the contributions of feedback and feedforward inhibition on spatial encoding. Another significant interneuron population, mossy cells, comprises the associational system of the dentate gyrus and contributes long-ranging projections along the dorso-ventral axis. We have previously explored the effects of mossy cells on network dynamics [27] and will also explore their role in spatial encoding.

Another aspect of place field generation and decoding that has yet to be addressed involves network oscillation which has been shown to encode spatial information [55]. As the large-scale model is able to generate spiking data for entire neural populations from which local field potentials can be predicted [56], it is uniquely situated to investigate the functional consequences of network oscillations. Computational studies have demonstrated the importance of oscillations for communicating information [57], [58], and further work will be performed to integrate the analysis of oscillations with typical spiking based methods.

V. Conclusion

The accessibility and interpretability of parameters allows parametric models of neural systems to simulate unique experiments and provide mechanistic explanations of the observed phenomena. The large-scale model presented here is novel in the scope and depth of detail included to describe biologically plausible population level activity approaching the full scale of a single hemisphere of rat hippocampus. With the introduction of grid cells as input, the output of the large-scale neuronal network model and the contributions of its model parameters can now be analyzed in the context of spatial cognition. In this work, the specific role of the axonal anatomy in the rat entorhinal-dentate system was investigated using simulations that would otherwise be impossible to recreate experimentally using present technology, and as such, this work offers one of the few investigations that could explain how network architecture within and between subfields, e.g., spatial processing between dentate gyrus and CA3/4 [59], affect neural encoding and neural system function. The successful inclusion of grid cells at this stage allows behaviorally relevant computational studies to be performed using the large-scale model as it is further expanded to include the CA3/4 and CA1/2 subfields, and the differences in feedforward connectivity that exist among the subfields will offer additional opportunities in studying how the differences in architecture, and other model elements, affect the processing of spatial information as it is successively transformed by the trisynaptic pathway.