Expected Label Value Computation for Atlas-Based Image Segmentation

Abstract

The use of multiple atlases is common in medical image segmentation. This typically requires deformable registration of the atlases (or the average atlas) to the new image, which is computationally expensive and susceptible to entrapment in local optima. We propose to instead consider the probability of all possible transformations and compute the expected label value (ELV), thereby not relying merely on the transformation resulting from the registration. Moreover, we do so without actually performing deformable registration, thus avoiding the associated computational costs. We evaluate our ELV computation approach by applying it to liver segmentation on a dataset of computed tomography (CT) images.

1. INTRODUCTION

Supervised automatic image segmentation is often a central step in medical imaging studies, enabling the analysis of specific regions of interest (ROIs). A training dataset is provided in supervised image segmentation, containing images that are each accompanied with manually delineated ROI labels. A new image is then segmented using the information from the training dataset. Two popular approaches to supervised image segmentation use multiple atlases [1–3] and deep neural networks [4]. In atlas-based segmentation of a new image, atlas images are (or a mean template image is) deformably registered to the new image. The manual labels are then propagated into the new image space using the computed transformations, and fused to form the new labels.

Being computationally very demanding, deformable image registration of the atlas images to the new image is the bottleneck of atlas-based segmentation. To improve computational efficiency, it has been proposed to use only a subset of atlas images [5], albeit at the price of discarding a portion of the available information.

The transformation resulting from registration guides the label propagation from the atlas to the new image. Being an iterative non-convex optimization, image registration is prone to entrapment in local optima, potentially leading to erroneous propagation of the labels. Moreover, equally reasonable transformations may produce close values for the registration objective function (within its margin of error). Thus, even if the global optimum is found, choosing it as the single correct transformation would mean disregarding valuable information provided by other potentially valid transformations. Uncertainty in registration has been incorporated into Bayesian segmentation by approximating the marginalization over registration parameters via Markov Chain Monte Carlo techniques [6], which, even though efficiently implemented, would further increase the computational costs. Local measures of uncertainty in deformable registration have also been used to improve the sensitivity of the label propagation in atlas-based segmentation [7].

In this work, we present a new atlas-based image soft-segmentation method that produces the expected value of a label at each voxel of the new image, while considering the probability of possible transformations, without explicitly sampling from the transformation distribution. Although accounting for deformations, we do not run deformable registration in either the training or the testing stages. We create a single image from the training data, which we call the key. Then, for a new image (after affine alignment), we compute the expected label value (ELV) map simply via a convolution with the key, which is efficiently performed using the fast Fourier transform. The soft segmentation provided by the ELV map can be further used to initiate a subsequent hard-segmentation procedure. We validate our approach through liver segmentation experiments on abdominal computed tomography (CT) images.

In the following, we describe the proposed method in detail (Section 2) and present experimental results (Section 3) along with some concluding remarks (Section 4).

2. METHODS

2.1. Segmentation from a Single Atlas

Let I: ℝ^d → ℝ be the d-dimensional image to be segmented, and J: ℝ^d → ℝ an atlas image with the same contrast as I, for which the manual label of a specific ROI has been provided as L: ℝ^d → {0,1}. For the new image I, we would like to compute the expected value of the ROI label, E: ℝ^d → [0,1], which is a measure of likelihood of each voxel belonging to the ROI.

In traditional atlas-based image segmentation, the label L is propagated into the space of I as L ∘ T*, where for the transformation T* the similarity between I and J ∘ T* is maximal.¹ Here, instead, we compute the expected value of the propagated L, while considering a probability for each possible transformation in $\mathbb{T}≔\{\mathit{T}:{\mathbb{R}}^d\to {\mathbb{R}}^d\}$, as follows:

$$E≔{\int }_{\mathbb{T}}\mathrm{Pr}(\mathit{T}|I,J)\left(L\circ \mathit{T}\right)\mathrm{d}\mathit{T}.$$ (1)

Equation (1) computes the ELV as an integral over the space of all transformations, which could be regarded as multiple (theoretically an infinite number of nested) integrals over the space of parameters representing T. For free-form deformation, as considered here, Eq. (1) in fact includes a d-dimensional integral – with respect to the value of T(x) – for each x ∈ ℝ^d.

The probability of the transformation given both the new and atlas images is proportional to:

$$\mathrm{Pr}(\mathit{T}|I,J)\propto \mathrm{Pr}(I,J|\mathit{T})\mathrm{Pr}\left(\mathit{T}\right),$$ (2)

where the two right-hand-side factors correspond to the image similarity and the transformation regularity, respectively. For the former, we opt to use the inner product of the image and the transformed atlas, since it is expected to be higher when the two images are well aligned:

$$\mathrm{Pr}(I,J|\mathit{T})\propto {\int }_{{\mathbb{R}}^d}I\left(\mathit{x}\right)\left(J\circ \mathit{T}\right)\left(\mathit{x}\right)\mathrm{d}\mathit{x}.$$ (3)

This would be the cross correlation of I and J if T were only a translation. It is, however, well established that the cross correlation reflects the degree of alignment more effectively when only the phase information of the image is included [8, 9], which is how in practice we will proceed, as described in Section 2.4.

Regarding the probability of the transformation, we will use the common Tikhonov prior on the regularity of the deformation field:

$$\mathrm{Pr}\left(\mathit{T}\right)\propto R(\mathit{T})≔e^{-\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^d}{\Vert \partial \mathit{T}\left(\mathit{z}\right)-\mathbb{I}\Vert }_F^2\mathrm{d}\mathit{z}},$$ (4)

where ∂T is the Jacobian matrix of T, $\mathbb{I}$ is the d × d identity matrix, and the constant parameter σ represents a prior on the magnitude of the deformations. By combining the above equations, the ELV at voxel y will be:

$$E\left(\mathit{y}\right)\propto {\int }_{{\mathbb{R}}^d}I(\mathit{x})\mathrm{d}\mathit{x}{\int }_{\mathbb{T}}\left(J\circ \mathit{T}\right)\left(\mathit{x}\right)\left(L\circ \mathit{T}\right)\left(\mathit{y}\right)R\left(\mathit{T}\right)\mathrm{d}\mathit{T}.$$ (5)

Since x and y are fixed in the inner integral, we make the change of variables T(z) = S(z − x). Note that such a global shift will not change either the regularization, i.e. R(T) = R(S), or the domain of the inner integral, $\mathbb{T}$. Consequently:

$$\begin{gathered} E\left(\mathit{y}\right)\propto {\int }_{{\mathbb{R}}^d}I(\mathit{x})\mathrm{d}\mathit{x}{\int }_{\mathbb{T}}\left(J\circ \mathit{S}\right)\left(\mathbf{0}\right)\left(L\circ \mathit{S}\right)\left(\mathit{y}-\mathit{x}\right)R\left(\mathit{S}\right)\mathrm{d}\mathit{S} \\ ={\int }_{{\mathbb{R}}^d}I\left(\mathit{x}\right)A\left(\mathit{y}-\mathit{x}\right)\mathrm{d}\mathit{x}, \end{gathered}$$ (6)

or:

$$E\propto I*A,$$ (7)

where * denotes the convolution, and we define the key, A, as:

$$A(\mathit{x})≔{\int }_{\mathbb{T}}\left(J\circ \mathit{S}\right)\left(\mathbf{0}\right)\left(L\circ \mathit{S}\right)\left(\mathit{x}\right)R\left(\mathit{S}\right)\mathrm{d}\mathit{S}.$$ (8)

Next, we write the transformation S as the sum of a global translation Δ ∈ ℝ^d and a deformation (displacement) field u ∈ U:

$$\mathit{S}\left(\mathit{x}\right)=\mathit{x}+\mathbf{\Delta }+\mathit{u}\left(\mathit{x}\right),$$ (9)

where $U≔\left\{\mathit{u}:{\mathbb{R}}^d\to {\mathbb{R}}^d\right|{\int }_{{\mathbb{R}}^d}\mathit{u}\left(\mathit{x}\right)\mathrm{d}\mathit{x}=\mathbf{0}\}$ is the set of translation-free displacement fields. The regularity prior is now:

$$R(\mathit{S})=\tilde{R}(\mathit{u})≔e^{-\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^d}{\Vert \partial \mathit{u}\left(\mathit{z}\right)\Vert }_F^2\mathrm{d}\mathit{z}}.$$ (10)

We combine the above three equations, and separate the integral over the space of all transformations into an integral over possible translation-free deformations and an integral over possible translations:

$$A\left(\mathit{x}\right)\propto {\int }_U\tilde{R}(\mathit{u})\mathrm{d}\mathit{u}{\int }_{{\mathbb{R}}^d}J\left(\mathbf{\Delta }+\mathit{u}\left(\mathbf{0}\right)\right)L\left(\mathit{x}+\mathbf{\Delta }+\mathit{u}\left(\mathit{x}\right)\right)\mathrm{d}\mathbf{\Delta }.$$ (11)

Note that this is a linear change of coordinates, hence dS ∝ dudΔ (with the ratio independent of S). With u and x being constant in the inner integral, we make the change of variables $\mathbf{\Delta }=\tilde{\mathbf{\Delta }}-\mathit{u}\left(\mathit{x}\right)-\mathit{x}$, leading to:

$$\begin{gathered} A(\mathit{x})\propto {\int }_U\tilde{R}(\mathit{u})\mathrm{d}\mathit{u}{\int }_{{\mathbb{R}}^d}J\left(\tilde{\mathbf{\Delta }}-\mathit{u}\left(\mathit{x}\right)+\mathit{u}\left(\mathbf{0}\right)-\mathit{x}\right)L\left(\tilde{\mathbf{\Delta }}\right)\mathrm{d}\tilde{\mathbf{\Delta }} \\ ={\int }_U\tilde{R}\left(\mathit{u}\right)B\left(\mathit{u}\left(\mathit{x}\right)-\mathit{u}\left(\mathbf{0}\right)+\mathit{x}\right)\mathrm{d}\mathit{u}, \end{gathered}$$ (12)

where B can be pre-computed from the atlas as:

$$B(\mathit{x})≔\left(J\left(-\mathit{x}\right)*L\left(\mathit{x}\right)\right)(\mathit{x}).$$ (13)

As can be seen, B is obtained by reversing the atlas image, blurring it by the label, and shifting it so the label ROI is roughly at the center. It can be verified that lim_σ→0 A = B. Next, we will analytically estimate the key, A, as a function of B for σ > 0.

2.2. Expectation over the Space of Deformations

Combining Eqs. (10) and (12) leads to:

$$A(\mathit{x})\propto {\int }_{U}B(\mathit{u}\left(\mathit{x}\right)-\mathit{u}\left(\mathbf{0}\right)+\mathit{x})e^{-\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^d}{\Vert \partial \mathit{u}\left(\mathit{z}\right)\Vert }_F^2\mathrm{d}\mathit{z}}\mathrm{d}\mathit{u}.$$ (14)

For simplicity, let us for now assume that x lies on the positive half of the first Cartesian coordinate axis, i.e., x = xv₁, where v₁ is the unit vector in the direction of the first axis, and x ≥ 0. We also define the line segment Q_x := {tv₁|0 ≤ t ≤ x}. Accordingly:

$$\mathit{u}\left(\mathit{x}\right)-\mathit{u}\left(\mathbf{0}\right)={\int }_{Q_x}\partial \mathit{u}\left({\mathit{x}}^{\prime }\right)\mathrm{d}{\mathit{x}}^{\prime }={\int }_0^x{\partial }_1\mathit{u}\left(t{\mathit{v}}_1\right)\mathrm{d}t,$$ (15)

where ∂₁u is the partial derivative of u in the direction of v₁. Therefore:

$$\begin{gathered} A(x{\mathit{v}}_1)\propto {\int }_{\partial U}B\left(x{\mathit{v}}_1+{\int }_0^x{\partial }_1\mathit{u}\left(t{\mathit{v}}_1\right)\mathrm{d}t\right) \\ \times e^{-\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^d}{\Vert \partial \mathit{u}\left(\mathit{z}\right)\Vert }_F^2\mathrm{d}\mathit{z}}\mathrm{d}(\partial \mathit{u}). \end{gathered}$$ (16)

Note that we made further simplification by integrating over the space of the Jacobian of the deformation, ∂U, instead of the space of the deformation, U, itself.²

In Eq. (16), the only values of ∂u on which B depends are ∂₁u(z) for z ∈ Q_x. Thus, we separate the integral into the product of three integrals, the first one being:

$$\begin{gathered} A(x{\mathit{v}}_1)\propto \underset{{\partial }_1\left\{\mathit{u}:Q_x\to {\mathbb{R}}^d\right\}}{\overset{⬚}{\int }}B\left(x{\mathit{v}}_1+{\int }_0^x{\partial }_1\mathit{u}\left(t{\mathit{v}}_1\right)\mathrm{d}t\right) \\ \times e^{-\frac{1}{2{\sigma }^2}{\int }_0^x{\Vert {\partial }_1\mathit{u}\left(t{\mathit{v}}_1\right)\Vert }_2^2\mathrm{d}t}\mathrm{d}({\partial }_1\mathit{u}), \end{gathered}$$ (17)

and the second and third integrals are:

$$\begin{gathered} \underset{{\partial }_1\left\{\mathit{u}:{\mathbb{R}}^d\backslash Q_x\to {\mathbb{R}}^d\right\}}{\overset{⬚}{\int }}{e}^{-\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^d\backslash Q_x}{\Vert {\partial }_1\mathit{u}\left(\mathit{z}\right)\Vert }_2^2\mathrm{d}\mathit{z}}\mathrm{d}({\partial }_1\mathit{u}) \\ \times \underset{{\partial }_{2,\dots ,d}U}{\overset{⬚}{\int }}{e}^{-\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^d}{\Vert {\partial }_{2,\dots ,d}\mathit{u}\left(\mathit{z}\right)\Vert }_F^2\mathrm{d}\mathit{z}}\mathrm{d}({\partial }_{2,\dots ,d}\mathit{u}), \end{gathered}$$ (18)

which are integrals of normal distributions and therefore constant, hence not included in the expression for A(xv₁) in Eq. (17).

Calculation of A(xv₁) can be made notationally easier by approximating the inner integrals in Eq. (17) as Riemann sums. We divide [0,x] into n equal intervals (n → ∞), with dt ≈ x/n, and define:

$${\mathit{q}}_k≔\frac{x}{n}{\partial }_1\mathit{u}\left(\frac{k}{n}x{\mathit{v}}_1\right).$$ (19)

The integral is now approximated as:

$$\begin{gathered} A(x{\mathit{v}}_1)\propto {\int }_{{\mathbb{R}}^{nd}}B\left(x{\mathit{v}}_1+\sum _{k=1}^n{\mathit{q}}_k\right) \\ \times e^{-\frac{1}{2x{\sigma }^2/n}{\sum }_{k=1}^n{\Vert {\mathit{q}}_k\Vert }_2^2}\mathrm{d}{\mathit{q}}_1\dots \mathrm{d}{\mathit{q}}_n. \end{gathered}$$ (20)

This is, in fact, n consecutive convolutions of B with a d-dimensional Gaussian,

$$A(x{\mathit{v}}_1)\propto {\left[B(\mathit{z})*\stackrel{n}{\overbrace{G\left(\mathit{z}\right|\mathbf{0},\frac{x}{n}{\sigma }^2\mathbb{I})\mathrm{*}\dots \mathrm{*}G(\mathit{z}\left|\mathbf{0},\frac{x}{n}{\sigma }^2\mathbb{I}\right)}}\right]}_{\mathit{z}=x{\mathit{v}}_1},$$ (21)

where G(·|μ,∑) represents the Gaussian function with the mean μ and the co-variance matrix ∑. Given that convolution of n identical Gaussians results in a Gaussian with n times the variance, we have:

$$A\left(x{\mathit{v}}_1\right)\propto {\left[B\left(\mathit{z}\right)*G(\mathit{z}|\mathbf{0},x{\sigma }^2\mathbb{I})\right]}_{\mathit{z}=x{\mathit{v}}_1}.$$ (22)

We now exploit the rotational invariance of the Gaussian in Eq. (22) and that of the Frobenius norm of the Jacobian in Eq. (14), to generalize Eq. (22) for any x ∈ ℝ^d:

$$A\left(\mathit{x}\right)\propto {\left[B\left(\mathit{z}\right)*G(\mathit{z}|\mathbf{0},{\Vert \mathit{x}\Vert }_2{\sigma }^2\mathbb{I})\right]}_{\mathit{z}=\mathit{x}}.$$ (23)

Despite our use of the convolution notation in Eq. (23), A is not computed via an actual convolution, because the co-variance matrix of the Gaussian kernel varies depending on x, where the result of the convolution is evaluated.

One can see that the key, A, is an inhomogeneously blurred version of B, where the size of the blurring kernel increases with the square root of the Euclidean distance from the center of B – i.e., the region corresponding to the label ROI (see Section 2.1). Blurring a region in A decreases its contribution to soft segmentation by removing its high-frequency components prior to the convolution in Eq. (7). This means that the proposed ELV takes local deformations into account by giving a smaller weighting to regions in the atlas image that are farther from the ROI, making the information in such far areas less important.

2.3. Multiple Atlases

In case N atlases (affinely normalized in the same space) with manual labels are available, we will write Eq. (1) in the same fashion, as:

$$E≔\frac{1}{N}\sum _{i=1}^N{\int }_{\mathbb{T}}\mathrm{Pr}(\mathit{T}|I,J_i)\left(L_i\circ \mathit{T}\right)\mathrm{d}\mathit{T},$$ (24)

where J_i and L_i are the i^th pair of atlas and manual label images, respectively. This will result in the same E and A as in Eqs. (7) and (23), with the only difference being the definition of B:

$$B\left(\mathit{x}\right)≔\frac{1}{N}\sum _{i=1}^N\left(J_i\left(-\mathit{x}\right)*L_i\left(\mathit{x}\right)\right)\left(\mathit{x}\right).$$ (25)

Note that even in the case of multiple atlases, A is a single image that is pre-computed from the training data.

2.4. Implementation

To create the key, A, we first ensure that the N training images are represented roughly in the same space; and if not, we affinely align them. We then generate B from Eq. (25), while for each convolution J_i(−x) * L_i(x) we compute:

$${\mathcal{F}}^{-1}\{\frac{{\widehat{J}}_i^{*}\left(\mathit{\omega }\right)}{\left|{\widehat{J}}_i\left(\mathit{\omega }\right)\right|}{\widehat{L}}_i(\mathit{\omega })\},$$ (26)

where the hat sign and ${\mathcal{F}}^{-1}$ represent the Fourier and inverse Fourier transforms, respectively. By only keeping the phase information of the image, we create a sharper probability distribution for the aligning transformation in Eq. (3) [8, 9]. In addition, removing the magnitude of ${\widehat{J}}_i$ has an intensity normalization effect, which prevents B from giving a different weighting to an atlas image due to its global intensity scaling. Next, we compute A voxel-wise from Eq. (23), by multiplying and summing B with a varying discretized Gaussian kernel.

To segment a new image, I, we first make sure that it is affinely aligned to the atlas space (if not, align it to the mean atlas image), and then compute the ELV map from Eq. (7) as follows:

$$E(\mathit{y})\propto {\mathcal{F}}^{-1}\{\frac{\widehat{I}\left(\mathit{\omega }\right)}{\left|\widehat{I}\left(\mathit{\omega }\right)\right|}\widehat{A}(\mathit{\omega })\}.$$ (27)

Once the initial ELV map is obtained, it can be refined by recalculating Eq. (27) while this time prioritizing the initial soft-segmented area. In our experiments, for instance, we used weighted versions of A(x) and I(x), as $A\left(\mathit{x}\right)G(\mathit{x}|\mathbf{0},s^2\mathbb{I})$ and $I\left(\mathit{x}\right){\left[E\left(\mathit{y}\right)*G(\mathit{y}|\mathbf{0},s^2\mathbb{I})\right]}_{\mathit{y}=\mathit{x}}$, respectively, where the size of the Gaussian window (2s) was half the image size.

Given that using the phase image discards some image intensity information, one can further augment the ELV volume with image intensities by multiplying E by the intensity prior,

$$\mathrm{Pr}(L_I|I,\left\{\left(J_i,L_i\right)\right\})\propto \mathrm{Pr}(I|L_I,\left\{\left(J_i,L_i\right)\right\})/\mathrm{Pr}(I|\left\{\left(J_i,L_i\right)\right\}),$$

where L_I represents the unknown label image corresponding to I. Pr(I|L_I,{(J_i,L_i)}) and Pr(I|{(J_i,L_i)}) can be approximated by Gaussian functions of the intensity values of I, with their parameters estimated from either the atlases, or the image itself using the initial ELV map. Several other post-processing steps are possible after this soft segmentation [1]. In our evaluation, we will use the thresholded ELV map as a seed region for subsequent hard segmentation.

The proposed model accounts for large translations, as well as local deformations, even though we do not run any deformable registration. As for rotation and global scaling, the local deformations can cover a small amount of them, and we do not expect a large amount given the initial affine alignment.

3. RESULTS AND DISCUSSION

We evaluated our ELV computation method on the training dataset of the public Liver Tumor Segmentation (LiTS) Challenge [10], which includes contrast-enhanced abdominal CT images with manually delineated labels for the normal tissue and lesions in the liver, provided by various clinical sites. We considered the entire (healthy and lesion) organ label in our experiments. 85 subjects passed our inclusion criteria, mainly the slice thickness being included in the header and no larger than 2mm. The images were resampled in the space of the first image to (1.6mm)³ isotropic resolution, so they were all of the size 248×248×323.

For each image, we created the key from the remainder of the images (i.e. the 84 “atlases”) following Eqs. (25) and (23), with a value of σ = 0.1, which was heuristically optimized during initial benchmarking. Next, as described in Section 2.4, we computed the ELV map in two levels (Figure 1, left). A supplementary video of the ELV maps for all subjects is available. To create a liver mask from the map (here and in the next steps), we thresholded the map to keep a voxel subset of the size of an average liver, which we estimated as the mean liver volume from the 84 atlas labels, and then refined the mask via morphological operations, by: eroding it using a spherical structuring element with the radius of 5 voxels, keeping the largest connected component, dilating it, and filling the holes.

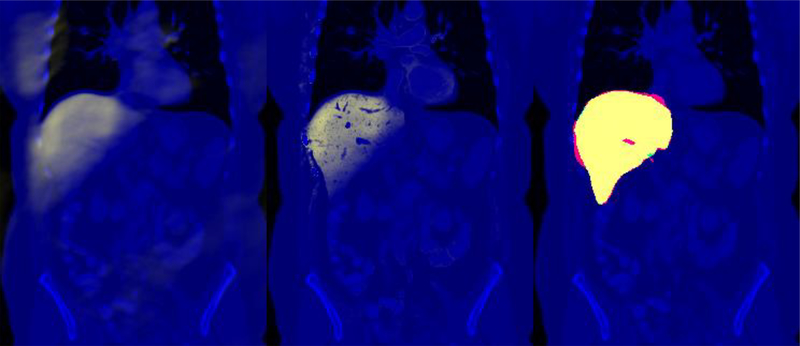
Figure 1.

CT image (blue) of the representative subject corresponding to the median segmentation Dice score. The slice with the largest cross section with the manual label is shown. Left: The ELV map of the liver (yellow). Middle: The ELV map modulated by the intensity prior (yellow). Right: The manual label (green), the segmentation result (red), and their overlap (yellow).

For the intensity-prior map, we used the initial ELV mask and its dilated version (by a sphere of radius 50) to estimate the mean intensity for the liver and the image, respectively. For stability, we estimated the standard deviation of the intensities from the 84 other subjects and their manual labels. Next, we modulated the ELV with the intensity prior (Figure 1, middle), created a new mask, and further refined it with an updated intensity mean estimated from this mask. The Dice overlap coefficients of these masks with the manual labels had a median of 0.86 across subjects (mean: 0.82 ± SEM 0.01). Note that the ELV map is computed via a simple linear convolution operation on the (phase) image, as opposed to mainstream supervised segmentation methods that include deformable registration or sophisticated trained neural networks.

Next, we used each mask to initialize an unsupervised segmentation algorithm based on the local center of mass [11]. For the intensity-prior map to be smooth, we computed it from a blurred version of the test image using a Gaussian with the standard deviation of 5 voxels. We ran the segmentation for 500 iterations with different values for the edge weighting parameter α (ranging from 100 to 2000), while not using the random phase (see [11] for details). We chose the value of α yielding the maximal Dice coefficient for each subject, leading to optimal Dice scores with a median of 0.91 (mean: 0.86 ± 0.02).³ Figure 1 illustrates the ELV and the segmentation results for the representative subject with the median Dice score. The seed mask – provided by the ELV – was indispensable to segment the liver with this unsupervised method.

For comparison, at the time of the submission of this article, the LiTS challenge website [10] reported Dice values for the healthy liver tissue ranging from 0.84 to 0.97, with many of the methods using deep learning. Note that here we aimed to estimate the entire organ label (healthy + lesion), therefore could not use the website for evaluation. Among those results of ours with lower (entire-organ) Dice scores, lesion regions were frequently the culprit, as the intensity-prior map, although generally improving the segmentation, had partially excluded some of those regions.

4. CONCLUSIONS

We have introduced a new approach to supervised soft-segmentation, which computes the expected label value (ELV) of an ROI from an image using a training dataset of atlases. The proposed method does not perform costly deformable registration, thereby also avoiding entrapment in local optima. We have evaluated our ELV computation technique in liver segmentation from CT images.

Supplementary Material

1

This video shows the computed ELV maps for the liver on all the 85 subjects. For each subject, the slice with the largest cross section with the ground-truth (manual) label of the liver is shown. The positive values, indicating the liver, are shown in red, and the negative values are in blue.