Exploring the dual functionality of an ytterbium complex for luminescence thermometry and slow magnetic relaxation

A combined experimental and theoretical approach reveals the intricacies related to an Yb^III complex, which functions dually as a SMM and a luminescent thermometer.

Abstract

We present a comprehensive investigation of the magnetic and optical properties of an ytterbium complex, which combines two desirable and practical features into a single molecular system. Based upon Yb^III ions that promote near-infrared optical activity and a chemical backbone that is ideal for an in-depth understanding of the magnetic behaviour, we have designed a multifunctional opto-magnetic species that operates as a luminescent thermometer and as a single-molecule magnet (SMM). Our magnetic investigations, in conjunction with ab initio calculations, reveal one of the highest energy barriers reported for an Yb^III-based complex. Moreover, we correlate this anisotropic barrier with the emission spectrum of the compound, wherein we provide a complete assignment of the energetic profile of the complex. Such studies lay the foundation for the design of exciting multi-faceted materials that are able to retain information at the single-molecule level and possess built-in thermal self-monitoring capabilities.

Introduction

Researchers in all fields of science regularly seek to control as many experimental variables as possible. This provides a means of rationalizing the processes that govern the outcome of the experiment, thus allowing for a more precise understanding of the dominant parameters that dictate the overall behaviour. In this regard, molecular systems are highly coveted due to their relative simplicity and the fact that they can often be systematically fine-tuned to study the effects of changing a single key feature.1–3 This is especially true for magnetic and optical systems, where high complexity compounds generally preclude an accurate comprehension of the observed properties. Indeed, while nanoparticles and high nuclearity clusters have shown great promise in their respective fields of optical spectroscopy4,5 and molecular magnetism,6,7 the underlying mechanisms that are at the heart of their exciting behaviours – i.e. energy transfer pathways and slow magnetic relaxation processes – remain elusive. As such, discrete molecular systems, based on one or two metal ions, have repeatedly been used as model compounds to uncover the origins of desirable properties.8–10 From a practical standpoint, the interest around these systems stems in part from the degree of miniaturization that they confer, with their properties being retained at the single-molecule level.11 This is a pivotal feature in view of foreseeable advanced applications, particularly for next-generation electro-magnetic devices where size limitations are often a stringent constraint.12 Therefore, discrete molecular systems are particularly appealing, since they readily allow for a comprehensive evaluation of the fundamental opto-magnetic properties, thus enabling the rational combination of multiple functionalities in a single system.

Here, we achieve the combination of magnetic and luminescence thermometric properties at a molecular level in a lanthanide (Ln^III)-based luminescent single-molecule magnet (SMM). The motivation for the current study stems from our previous investigations into a series of robust dinuclear Ln^III complexes, formulated as [Ln^III₂(valdien)₂(NO₃)₂],1,13 where valdien represents the doubly deprotonated form of N1,N3-bis(3-methoxysalicylidene)diethylenetriamine. While the Dy^III analogue isplays modest slow magnetic relaxation parameters,13 we sought to design an innovative opto-magnetic species using the same chemical backbone. This rather straightforward dinuclear model – both from a chemical and electronic energy scheme viewpoint – allows for an in-depth interpretation of both the photoluminescence and dominant magnetic relaxation pathways. Although Yb^III is a rather unorthodox choice for the preparation of purely magnetic systems, the interest around this new class of compounds is currently increasing for their potential in generating novel opto-magnetic species.14,15 With this in mind, our strategy consists of utilizing Yb^III ions, that exhibit near-infrared (NIR) optical activity for the design and synthesis of multifunctional luminescent SMMs.16–18 This, paired with the NIR optical activity of this Ln^III ion, makes Yb^III SMMs promising multifunctional opto-magnetic species. Moreover, the emission of Yb^III complexes has been shown to be a suitable tool to probe environmental changes such as temperature19 and viscosity20 variation, hence increasing the appeal of such systems from an application standpoint.

Further to this, intense research efforts on molecular junctions have recently targeted the realization of quantum computing and molecular electronics. Advances in this area by Wernsdorfer and co-workers include the elegant manipulation of single spins of a SMM (TbPc₂) using an electrical field.21 At the same time, Lee et al. reported a critical study on the heat dissipation in such single-molecule junctions.22 The generation of heat in electrical circuits, resulting from the movement of charged species, is an important issue to address, and particularly relevant for junctions based on SMMs, as the excess energy may significantly alter the magnetic relaxation dynamics of these molecules and thus their functionality. It is not feasible to carefully probe such temperature variations at a molecular level using conventional contact thermometers. Instead luminescence thermometry is a valuable tool in this context.23–25

As such, we provide a proof-of-concept for the design of molecules acting as self-calibrated contactless luminescent thermometers, while also displaying SMM behaviour. The combination of two such properties is ideal for monitoring and advancing molecular junctions based on SMMs and manipulated using electrical fields. We present our findings into the dual functionality of an Yb^III dimer behaving not only as one of the highest performing Yb^III-based SMMs reported so far, but also as a molecular luminescent thermometer capable of operating over a broad temperature range (80–320 K). Considering the recent advances towards extending the operational capabilities of SMMs above liquid nitrogen temperatures (77 K),26–29 and conversely, the outstanding results in terms of luminescent thermometers efficiently operating at the cryogenic regime,30 we foresee the exciting prospect of eventually achieving an overlap between the working range of the SMM and the molecular luminescent thermometer. This would allow for in situ and real-time contactless thermal readouts during SMM operation. It should also be noted that optical measurements performed on a single-molecule junction would be non-trivial and constitute a challenging task. In addition, while an overlap of the functioning temperature range between the two properties has yet to be achieved, the present study provides a blueprint for the design and preparation of an innovative class of SMMs with built-in thermal self-monitoring properties.

Results and discussion

Structural characterization

The dinuclear [Yb₂(valdien)₂(NO₃)₂] complex was synthesized in analogous fashion to the previous set of reported [Ln₂(valdien)₂(NO₃)₂] dimers.13 Due to the isostructural nature of the {Yb₂} complex to the well investigated {Dy₂} systems, only the key structural features will be presented here. The centrosymmetric complex crystallizes in the triclinic P1[combining macron] space group and consists of two Yb^III ions bridged by a pair of phenoxide moieties belonging to the valdien^2– ligand, while terminal NO₃^– groups serve as capping molecules. Full crystallographic details can be found in Table S1.† The intramolecular Yb^III–Yb^III distance of 3.708(6) Å is significantly shorter than the Dy^III–Dy^III distance of 3.768(3) Å. This stems from the expected contraction of the Ln^III–O bond lengths, as the ionic radius of the Ln^III ion decreases, in line with the effects of lanthanide contraction. Despite this shortening, the Yb^III–O–Yb^III bridging angle was calculated to be 108.2°, the same as for the {Dy₂} analogue.13 Also of optical and magnetic relevance is the shortest intermolecular Yb^III–Yb^III distance, which was determined to be 7.40 Å. Other relevant bond distances and angles can be found in Table S2.†

Magnetic properties

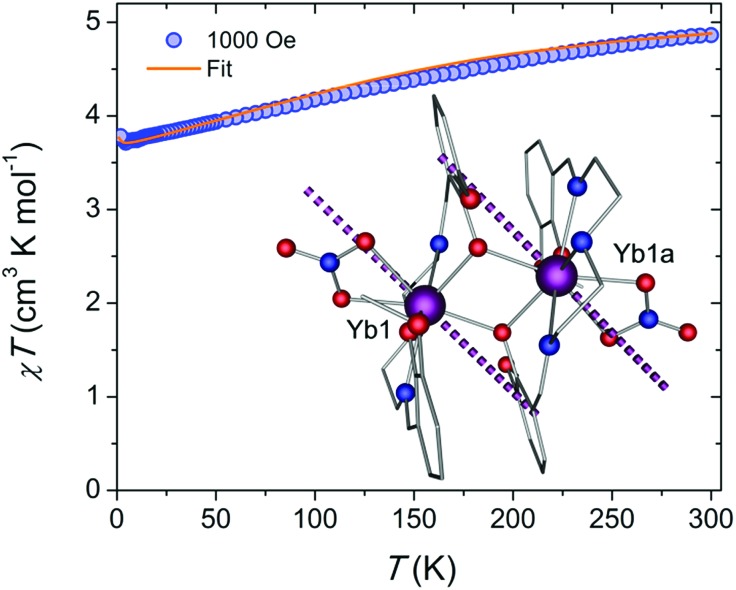
To correlate the structural and magnetic features of the proposed system, we first evaluated the dc magnetic susceptibility, χ, under a field of 1000 Oe and in the temperature range of 1.9–300 K. The corresponding χT vs. T plot (Fig. 1) reveals a room temperature χT value of 4.86 cm³ K mol^–1, which is close to the theoretical value of 5.14 cm³ K mol^–1 for two non-interacting Yb^III ions. Upon cooling, we observe a steady decrease of the χT product, down to a minimum of 3.71 cm³ K mol^–1 at 4.5 K. Such a decrease in the χT can be attributed to the thermal depopulation of the higher-energy Stark sublevels and is well reproduced by ab initio crystal field calculations. Further cooling results in a small uptick to 3.78 cm³ K mol^–1 at 1.9 K that can be provisionally explained by the presence of weak ferromagnetic interactions.18,31 According to the broken-symmetry DFT (BS-DFT) analysis however, the intramolecular exchange interaction is antiferromagnetic (–0.7 cm^–1), but this approach can provide only an estimate of J as it operates with S = 1/2 in the absence of spin–orbit coupling.32 Dipolar interaction estimates based on the crystal structure and ab initio crystal field parameters are also predicted to stabilize non-magnetic sublevels. Such low temperature increases in the χT product have been observed in similar Yb₂ SMMs and may be due to weak ferromagnetic interactions between the spin centres.18 Based on the fitting of the crystal field parameters however, such an approach failed to fit both M(H) and χT(T) data simultaneously. In contrast, here we keep the ab initio crystal field parameters and dipolar interaction fixed and fit only the exchange coupling. In this way, both M(H) and χT(T) plots match well the experimental data (Fig. 1 and S1A†). Field dependence of the magnetization (Fig. S1A†) displays typical behaviour for weakly interacting Yb^III ions, with near saturation and a value of 4.11 μ_B at 1.9 K and 7 T. Moreover, the M vs. H/T plot (Fig. S1B†) reveals isotemperature curves that are nearly superimposed, suggesting only minor magnetic axiality. Large magnetic axiality is a key component in the observation of slow relaxation of the magnetization at zero field. Ab initio analysis predicts a significant transverse component in the effective g-tensor of the lowest Kramers doublet (KD) for each Yb^III ion g_eff = (7.5724, 0.5669, 0.9183). The orientation of the main magnetic axis of the lowest KD is shown in Fig. 1.

Fig. 1. Temperature dependence of the χT product at 1000 Oe (blue spheres), and comparison with the calculated magnetic susceptibility assuming J = 0.005 cm^–1 (solid orange line). The inset displays the molecular structure of the {Yb₂} complex along with the orientation of the main magnetic axis in the ground state of the Yb^III ions as shown in the purple dashed lines. Colour code: purple (Yb), red (O), blue (N); while all unfilled grey vertices represent carbon atoms.

To evaluate the performance of the Yb^III-based dimer for slow relaxation of the magnetization, which may originate from significant separation between the ground and first excited state (vide infra), ac susceptibility measurements were performed at 1.9 K and varying dc fields (Fig. S2†). This data was fit to a generalized Debye model with the best fit parameters given in Table S3.† At zero dc field, no out-of-phase signal was observed, likely due to quantum tunnelling of the magnetization (QTM), which is enabled by the mixture of the M_J levels in the ground state due to the absence of axiality, as shown by the g-tensors. The application of a small dc field, however, reveals a clear out-of-phase signal. Such field induced SMM-like behavior has regularly been observed in Yb-based systems.

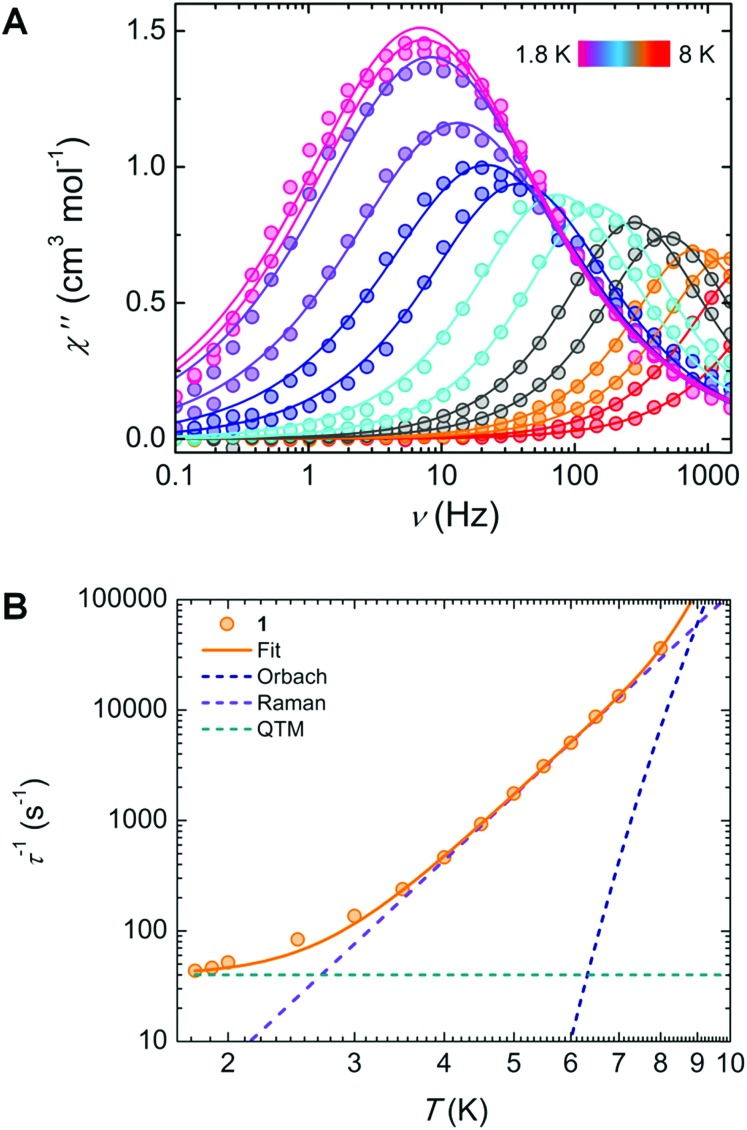
Under a static dc field of 1000 Oe, the signal of the ac magnetic susceptibility was optimized in the frequency range of 0.1 to 1500 Hz where an out-of-phase signal was observed up to 8 K (Fig. 2A). These data were fit to a generalized Debye model from which a distribution (α) of relaxation times (τ) can be extracted (Table S4†).

Fig. 2. (A) Frequency dependence of the out-of-phase (χ′′) magnetic susceptibility under a 1000 Oe dc field, with the solid lines representing the best fit to a generalized Debye model. (B) Temperature dependence of the magnetization relaxation times (τ), with the solid line representing the best fit using eqn (1), and dashed lines indicating their individual contributions to the relaxation.

Further insights into the magnetic relaxation processes of the complex was achieved by evaluating the τ^–1vs. T plot (Fig. 2B). The best-fit was obtained by considering contributions from Orbach, Raman, and quantum tunnelling of the magnetization (QTM):

τ^–1 = τ₀^–1 exp(–U_eff/k_BT) + CTⁿ + τ_QTM^–1 1

The resulting best-fit parameters are τ₀ = 4.62(3) × 10^–8 s, U_eff/k_B = 65.58(2) K, C = 0.097(5) s^–1 K^–6.06 , n = 6.0(6) and τ_QTM = 2.21(1) × 10^–2 (Fig. 2B). Below 3 K, we can observe the onset of QTM. The peaks in Fig. 2A that begin to superimpose are also a clear indication of this process becoming predominant. In the intermediate temperature range (4–7 K), the linearly increasing τ^–1 values plotted on a logarithmic scale confirm the presence of a Raman relaxation process. Finally, at high temperatures (>7 K), deviation from this linearity might suggest the onset of an Orbach relaxation mechanism, which has been observed in a limited number of Yb^III-based complexes.16 In fact, to the best of our knowledge, a U_eff of ∼65.5 K (45 cm^–1) is the highest energy barrier reported for an Yb^III SMM.33 Despite this, a significant discrepancy exists between the energy barrier determined from ac measurements, from spectroscopic evidence, and from ab initio calculations: 45.5, 382.5 and 296 cm^–1, respectively (vide infra). We infer from this that a pure Orbach model is insufficient to adequately describe the molecular system, as demonstrated by the presence of Raman and QTM terms in the τ^–1vs. T plot. Thus, it should be noted that the Orbach process, seen mainly at high temperatures, can be removed to fit the τ^–1vs. T data using only Raman and QTM mechanisms (Fig. S3†). The lack of a real state necessary for an Orbach process around the value of the energy barrier (50–70 K) further supports this conclusion. The Raman and QTM parameters for this fit were kept identical to the previously described model. Such behaviour is not surprising given the fact the slow relaxation of the magnetization was enhanced under an applied field. We have also examined the dependence of τ with an applied field, taking into account direct, QTM, Orbach and Raman processes.

τ^–1 = AH⁴T + B₁/(1 + B₂H²) + τ₀^–1 exp(–U_eff/k_BT) + CTⁿ 2

For the data collected at 1.9 K, the resulting fit parameters are A = 2.44(4) × 10^–12 s^–1 K^–1 Oe^–4, B₁ = 236.3 s^–1 and B₂ = 5.64(1) × 10^–6 Oe^–2, (Fig. S4†). It is noteworthy that the values for the thermally activated and Raman processes were kept constant from the previous fit in order to avoid over parameterization. By plotting τ vs. H (Fig. S5†), it can be seen that τ begins to plateau around 1400 Oe, suggesting that the direct process may begin to contribute more at higher fields. The increase in the relaxation times at low fields, from 200 to 1200 Oe, is explained in the following section.

Electronic structure calculations

The computed ligand field splitting of the ²F_5/2 and ²F_7/2 terms revealed a significant gap of 296 cm^–1 between the two lowest KDs. The well-isolated ground KD features pronounced anisotropy of the effective g-tensor and almost pure M_J = 7/2 wavefunction. This is not typical for eight-coordinated Yb^III complexes that usually exhibit a square antiprism coordination geometry. Such anisotropy is more common for trigonal or axial arrangements.31

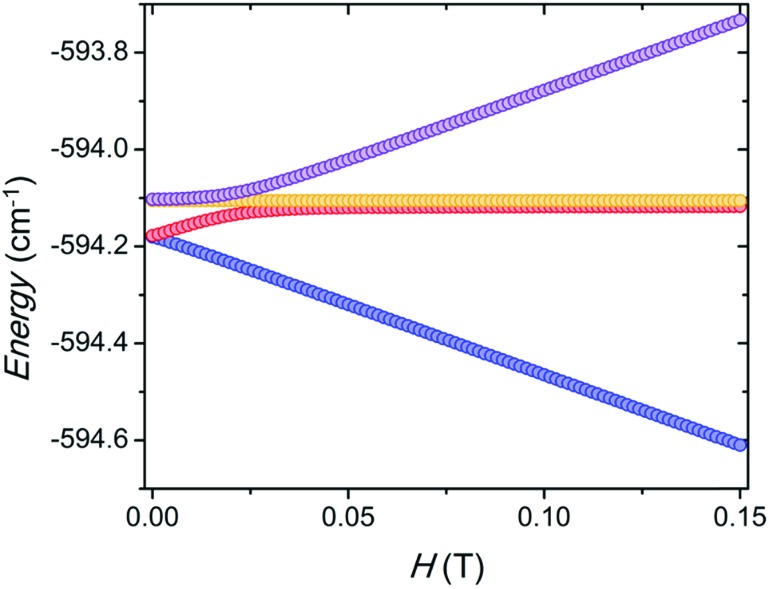
The BS-DFT calculation of the coupling between the two Yb^III centers predicts an antiferromagnetic exchange. However, as previously mentioned, the magnetic susceptibility has a small increase at low temperature that can be simulated only with a ferromagnetic interaction of J_ex = 0.005 cm^–1 taking into account a fixed dipolar interaction of J_dip = –0.004 cm^–1 as defined by the structure. Additionally, the magnetic susceptibility above 15 K is well reproduced by the ab initio model without any coupling. This small ferromagnetic exchange coupling stabilizes the magnetic sublevels by about 0.1 cm^–1. When the magnetic field is applied along the main magnetic axis of the lowest KD for each Yb^III, the level avoiding crossing is centred around 0.025 T (Fig. 3). This is consistent with the observed monotonic increase of the relaxation times with the application of a magnetic field above 0.02 T, as it decouples the magnetic sublevels (Fig. S5†).

Fig. 3. Energy of the four lowest sublevels of the coupled system taking into account dipolar and exchange interactions. The magnetic field is applied along the main magnetic axis of the lowest KD of the individual Yb^III metal centre.

Spectroscopic measurements

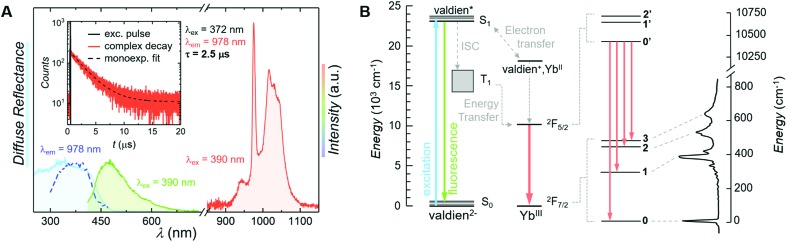
The beauty of the proposed system resides in the uncomplicated nature of its chemical structure and the simple two-level energy scheme of Yb^III, the combination of which yet endows the complex with a rich set of physical properties. To that end, along with promoting the magnetic behaviour of [Yb₂(valdien)₂(NO₃)₂], the ligand scaffold ensures absorption of light in the UV-blue optical range (Fig. 4A). The absorption properties are mirrored by the excitation spectrum, which shows sensitization of Yb^III NIR emission achieved via ligand excitation (Fig. 4A). The emission spectrum recorded at room temperature under 390 nm excitation is characterized by an intense line at approximately 978 nm assigned to the Yb^III : ²F_5/2 → ²F_7/2 transition. A weak contribution from the ligand fluorescence around 490 nm is also noticeable – this, along with the solid-state absorption spectrum, was used to locate the singlet state S₁ of the complex at approximately 23 090 cm^–1. The sensitized emission of Yb^III can occur either through energy or electron transfer from the ligand (Fig. 4B).34–37 The latter mechanism is particularly prominent in Ln^III ions that can be reduced to their Ln^II form, as it is the case for Yb^III.38 Both mechanisms entail light absorption from the ligand (i.e. the valdien moiety in the proposed {Yb₂} complex) with a consequent promotion of an electron to the excited singlet state (S₁). From there, two scenarios are possible. In one case, the ligand can undergo intersystem crossing (ISC) to the triplet state (T₁) followed by energy transfer to the Yb^III : ²F_5/2 state, eventually leading to the radiative decay to the ground state (Yb^III : ²F_7/2). Alternatively, the ligand in its excited state transfers an electron to Yb^III, thus reducing it to Yb^II. This is followed by electron back-transfer to the ligand, yielding re-oxidised Yb^III. If the correspondingly released energy is enough to populate the Yb^III excited state (²F_5/2), lanthanide emission is observed. Both sensitization pathways are plausible for this system and the findings reported below do not depend on the nature of the sensitization process.

Fig. 4. (A) Spectroscopic characterization of the luminescent SMM proposed in this study. Solid state absorption spectrum (cyan), excitation spectrum recorded monitoring the emission at 978 nm (blue) and emission spectra in the visible (green) and NIR (orange) range recorded exciting at 390 nm. In the inset: photoluminescence kinetics (orange) recorded exciting the system at 372 nm and monitoring the emission at 978 nm, along with its mono-exponential fit (dashed black line). The solid black line is the laser signal. (B) Energy level scheme with the main transitions observed in the system (same colour code as (A)) and proposed Yb^III sensitization mechanisms. The Stark sublevels are sketched according to the results of ab initio calculations and are correlated to the transitions observed in the emission spectrum of the complex recorded at 77 K under 375 nm excitation.

In spite of the rather simple electronic structure of this Ln^III ion, it has been often challenging to interpret the spectroscopic data of Yb^III complexes and to accurately retrieve the actual energy level scheme of the investigated system.14 This is mainly due to the usual strong contribution of vibronic sidebands in systems based on Yb^III.39 For this reason, we sought support from ab initio calculations and compared these results with low-temperature spectroscopic measurements, thus assigning the observed transitions accordingly (Fig. 4B and Table 1). To thoroughly characterize the complex from a spectroscopic standpoint, emission decay (inset in Fig. 4A) and photoluminescence quantum yield (PLQY) measurements were carried out. The photoluminescence lifetime of the proposed SMM under indirect (ligand-sensitized) excitation of Yb^III at 372 nm is 2.5 μs, a small value compared to most luminescent systems based on this lanthanide ion, but in line with those reported for other Yb^III complexes.15,40,41 We ascribe the relatively short lifetime of this complex, as well as the modest PLQY (vide infra), to the detrimental effect of the amine moiety in the valdien ligand on the optical performance of the system – since the high-energy vibrations of this group support the phonon-assisted de-excitation of excited levels. The lifetime of the Yb^III : ²F_5/2 level was also investigated by directly exciting the lanthanide ion at 976 nm (Fig. S6†), attaining a decay time of approximately 2.8 μs. Considering a 10 % error on the measurements and the rapid decay rate, the lifetimes obtained under direct and indirect Yb^III excitation are comparable. The slightly faster lifetime obtained under indirect excitation of Yb^III through the ligand could be explained due to the presence of additional, non-radiative de-excitation pathways that are otherwise not available under direct excitation of the lanthanide ion. These results are not surprising, since excitation wavelength-dependent lifetimes were already observed previously.42

Table 1. Energy of the Kramers doublets (KDs) as obtained from ab initio calculations and from spectroscopy measurements, corresponding effective g-tensors and the largest |M_J| contribution to the wave function computed with SOC-CASSCF/RASSI.

Term	Energy, cm–1		|MJ|	g′eff
	From calculations	From spectroscopy
2F7/2	0	0	7/2–90%	7.5724	0.5669	0.9183
	296	382.5	5/2–58%	5.8047	2.2362	1.3143
	421	530.4	1/2–49%	7.3383	0.7869	0.571
	472	641.9	3/2–44%	6.6627	1.3736	0.9008
2F5/2	10 351	10 224.9	—	4.0128	0.4209	0.6562
	10 647	—	—	2.9585	0.347	1.3231
	10 743	—	—	2.8724	0.8907	1.5597

An estimation of the PLQY could be obtained from the ratio between the observed decay time and the intrinsic Yb^III radiative lifetime, usually considered to be 1.2 ms.43,44 The PLQY obtained from this procedure is 0.21 %. Absolute PLQY measurements were also performed with the aid of an integrating sphere. For these measurements, an excitation wavelength of 372 nm and two different non-emissive blanks (BaSO₄ and an empty cell) were used. The number of emitted photons was derived from the integration of the Yb^III emission spectrum over the 900–1060 nm range. This provides a PLQY in the range of 0.4–0.5% (see Table S5 and Fig. S7 and S8†). The obtained mean value of 0.43 ± 0.07% is comparable to the values reported in the literature for other Yb^III complexes (Table S6†). Nonetheless, the comparison of PLQY values reported for different Yb^III-based systems is problematic due to a series of potential sources of uncertainty related to: (i) the reliability of the spectral emission correction curve of the detector,45 (ii) reabsorption phenomena by other Yb^III ions in the system (particularly prominent in case of measurements on closely-packed crystal structures), (iii) the choice of a suitable blank46 (again greatly impacting the results in case of measurements on powders or crystals), and (iv) the selection of the range over which the integration of the emission signal is performed.47 Considering all these sources of uncertainty, and given the small value observed for this system, uncertainties in the order of 30 % could be encountered. Similar uncertainties (intended as overall uncertainties, exceeding the typically provided relative standard deviations of fluorescent measurements – see discussion in the ESI†)48,49 have to be considered also for the values reported in Table S6.†

Luminescence thermometry

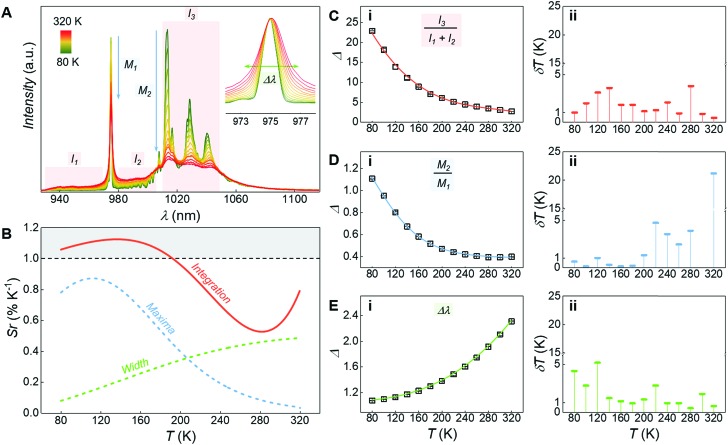
The system under study behaves as a luminescent thermometer over the 80–320 K temperature range (Fig. 5). Different self-calibrated50,51 optothermometric approaches were explored, all based on variations of the emission profile associated to the Yb^III : ²F_5/2 → ²F_7/2 transition (Fig. 5A). The most sensitive thermometric approach (Fig. 5B – Integration) was obtained when considering as the thermometric parameter (Δ) the ratio between the integrated intensity of the low-energy side of the considered band (I₃) and the sum of two regions located at higher energy (I₁ and I₂ – Fig. 5C(i)). Assignation of the signals in the considered ranges is not trivial since the emission spectra of Yb^III complexes are heavily influenced by electron-phonon coupling52,53 (see ESI and Fig. S8† for additional discussion). Here we do not attempt to identify the electronic processes involved in the variation of the spectral profile. Importantly, the sensitivity of the proposed thermometric method is above unity between 80 to 200 K and does not fall below 0.5 % K^–1 throughout the whole temperature range tested (Fig. 5B), with an associated uncertainty below 4 K (Fig. 5C(ii)).

Fig. 5. (A) Emission spectra arising from the Yb^III : ²F_5/2 → ²F_7/2 transition recorded under 375 nm excitation at different temperatures (from 80 to 320 K). In the inset, a zoom-in of the 0′–0 Stark component is shown. (B) Sensitivities (S_r) of the optothermometric approache relying on the three different thermometric parameters (Δ). In (C–E) the thermometric parameters for the three optothermometric approaches are reported (C(i) – ratio between integrated regions I₁, I₂, and I₃; D(i) – ratio between 0′–0 and 0′–1 Stark components; E(i) – 0′–0 peak width) along with the respective fits (C(i) and E(i) – cubic function; D(i) – Boltzmann function; as implemented in OriginPro® software), and their associated uncertainties (ii). In A, red shaded areas indicate the integration ranges (I₁, I₂, I₃) used for the first luminescence thermometry approach, blue arrows evidence the intensity drop of the Stark components used for the second approach, and the green double-headed arrow in the inset highlights the broadening of the 0′–0 Stark component upon increasing the temperature. In B, the region for S_r > 1 % K^–1 is highlighted with a grey-shaded area.

To further investigate the possibility of using the Yb^III complex as a luminescent thermometer, two additional optothermometric approaches were tested. A straightforward method relies on the ratio between the maxima of the 0′–0 (M₁) and 0′–1 (M₂) Stark components of the ²F_5/2 → ²F_7/2 Yb^III manifold (Fig. 5B – Maxima – and D(i)). Another approach is based on the inhomogeneous broadening of the emission profile that follows the temperature-dependent increase of phonon density – which is sizeable when considering the narrow emission lines of lanthanide-based systems.54–57 Hence, the half width at half maximum of the ²F_5/2 → ²F_7/2 manifold 0′–0 component (Δλ) was also evaluated as a thermometric parameter (Fig. 5B – Width – and E(i)). However, both approaches showcase an overall lower sensitivity compared to the one based on the integration procedure (Fig. 5B).

In all three cases, the variation of the thermometric parameters versus temperature was fitted using empirical functions. Their numerical derivatives were used to calculate the relative sensitivities (S_r) of the thermometric approaches (Fig. 5B),58 and from them the associated uncertainties (Fig. 5C(ii), D(ii) and E(ii)).59 The relative sensitivity reported for this system is slightly lower than the one of other luminescent metal coordination complexes.11,60–63 However, those systems were purposely designed to act as luminescent thermometers mainly benefiting from the energy transfer among different lanthanide ions. Moreover, they often self-assemble in extended metal–organic frameworks (MOFs) and they fully operate in the visible optical region (where the detection systems generally allow for a more accurate signal readout). Instead, here luminescence thermometry is achieved exploiting a single band in the NIR region from a single pair of Yb^III ions, in a system optimized to also operate as a SMM.

Conclusions

Here, opto-magnetic investigations into an Yb^III complex have precisely outlined the mechanisms that govern its unique SMM and optothermometric properties. The complementary combination of magnetic, optical and computational evidence provides unequivocal insights into the origins of this dual functionality. Thus, we have assessed one of the highest energy barriers for an Yb^III-based complex, while also establishing the sensitivity of the emission spectrum under UV excitation to temperature variations. The foregoing results demonstrate a unique example where we exceed the conventional study of Ln^III SMM behaviour by introducing a second practical functionality to the molecular system. While further progress is necessary to achieve an overlap between the two working temperature ranges required for both SMM and luminescence thermometry operations, we nevertheless propose an exciting avenue for novel and dually functioning single-molecular materials that can potentially stimulate further studies in the fields of SMM and luminescence thermometry.

Experimental section

All manipulations were performed under aerobic conditions using chemicals and solvents from commercial sources (Strem Chemicals, TCI America, and Fisher Scientific) and used as received without further purification.

Synthesis of N1,N3-bis(3-methoxysalicylidene)diethylenetriamine (H₂valdien)

The H₂valdien ligand was synthesized in accordance with previously published procedures.13

Synthesis of [Yb₂(valdien)₂(NO₃)₂]

To a solution of H₂valdien (0.125 mmol, 0.046 g) and triethylamine (0.25 mmol, 35 μL) in 5 mL of DMF was added Yb(NO₃)₃·5H₂O (0.125 mmol, 0.056 g) dissolved in 5 mL of MeOH. The resulting reaction mixture was stirred for 1 min and filtered. The filtrate was then left undisturbed in a diethylether bath for 4–5 days, after which yellow rectangular crystals were isolated in approx. 30% yield. Selected IR (cm^–1): 3222 (m), 2964 (w), 2917 (w), 2853 (w), 1637 (m), 1622 (s), 1594 (w), 1551 (w), 1448 (s), 1402 (m), 1352 (w), 1327 (w), 1299 (s), 1262 (s), 1238 (s), 1228 (s), 1195 (w), 1163 (w), 1111 (m), 1083 (m), 787 (w), 739 (s), 725 (s), 630 (m), 605 (w). Elemental analysis; expected: C 39.73%, H 3.83 %, N 9.27%; found: C 39.60%, H 3.25 %, N 9.37 %.

Single crystal X-ray diffraction

Single crystal X-ray diffraction data were collected at 200(2) K on a Bruker Kappa Apex II CCD diffractometer with graphite-monochromatised Mo-Kα radiation. Data collection and processing were performed with the Bruker APEX II software packages64 The structure was solved by Direct methods using SHELXL and refined on F2 by full matrix least-squares technique with SHELXL using the Olex2 (v.1.2.9) program package.65 Anisotropic displacement parameters were applied for all atoms, expect hydrogen atoms. These were calculated in their positions or located from the electron density map and refined as riding atoms using isotropic displacement parameters.

Infrared (IR) spectroscopy

IR analyses were performed with a Nicolet 6700 FT-IR spectrometer equipped with an attenuated total reflectance (ATR) accessory in the 4000–600 cm^–1 range.

Magnetic measurements

Magnetic susceptibility measurements were performed using an MPMS-XL7 Quantum Design SQUID magnetometer. Direct current (dc) susceptibility measurements were performed at temperatures ranging from 1.9 to 300 K, and up to applied fields of 7 T. Measurements were performed on a crushed polycrystalline sample of 12.7 mg, and wrapped in a polyethylene membrane. Alternating current (ac) susceptibility measurements were performed under an oscillating ac field of 3.78 Oe and ac frequencies ranging from 0.1 to 1488 Hz. Magnetization versus field measurements were performed at 100 K in order to check for the presence of ferromagnetic impurities, which were found to be absent in all samples. Magnetic data was corrected for diamagnetic contributions using Pascal's constants.

Luminescence measurements

The luminescence decay under ligand excitation was measured using an Edinburgh Instruments FLS920 fluorescence lifetime spectrometer equipped with an EPL-375 picosecond pulsed diode laser set to 50 kHz (repetition rate of 20 μs) with maximum emission at 372 nm. The luminescence decay under direct Yb excitation was measured using an Edinburgh instruments FLS980 fluorescence lifetime spectrometer equipped with a 980 nm pulsed diode laser set to 100 Hz (repetition rate of 10 ms). Luminescence lifetimes were mono-exponentially fitted from the obtained luminescence decay data using FAST.

The emission spectra at room temperature were acquired with an independently calibrated FSP920 spectrofluorometer (Edinburgh Instruments; 300–1700 nm) equipped with three different detectors and exciting the complex at 390 nm.46

Absolute photoluminescence quantum yield (PLQY) measurements were performed with a custom designed integrating sphere setup as previously reported.66 The powdered sample was measured using a demountable quartz glass circular cell with a path length of 0.05 mm. For excitation, an Edinburgh Instruments EPL-375 picosecond pulsed diode laser (peak power 0.14 W) was used with maximum emission at 372 nm.

Temperature-dependent photoluminescence data were obtained on a Fluorolog-3 spectrofluorometer (Horiba FL3-22-iHR320). An ozone-free Xenon lamp of 450 W (Ushio) was used as a radiation source, selecting an excitation wavelength of 375 nm. The emission spectra were recorded using an iHR320 emission monochromator and a Hamamatsu H10330A-75 photomultiplier. The sample was placed inside a Janis VNF-100 cryostat controlled by a Cryocon 32B temperature controller. The temperature was lowered to 80 K and gradually increased to 320 K. For each step, upon reaching the target temperature, 10 min were waited to guarantee thermal stabilization.

Ab initio calculations

Electronic structure calculations, where one of the Yb was substituted with diamagnetic Y, was performed with MOLCAS 8.0 (ref. 67) program with the following basis set: Yb and Y – ANO-RCC-VTZP; O and N – ANO-RCC-VDZP, C and H – ANO-RCC-VDZ.68–70 Cholesky decomposition with the “high” accuracy threshold was used for the two-electron integrals to speed up the calculation and reduce memory requirements.71,72 Scalar relativistic effects were accounted using second order Douglas–Kroll–Hess approximation.73 Active space for CASSCF74 calculation of spin-free states consists of seven 4f orbitals with 13 electrons for Yb^III. Spin–orbit coupling was computed using the mean-field approximation75 as implemented in RASSI. Molar magnetic susceptibility and magnetization were computed using SINGLE_ANISO76 routine together with the ligand field parameters for Stevens operator equivalence representation of the ground term with the total momentum J = 7/2.77

Dipolar and exchange interaction were computed using Spinach78 package for spin dynamics calculations employing the Stevens operator equivalence approach.79 The total Hamiltonian can be written as following:

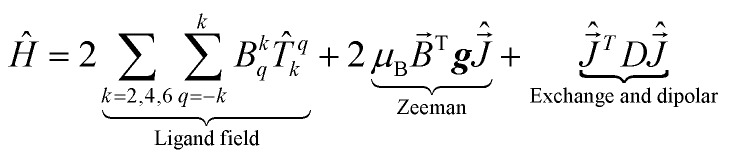3

where Bkq are the ligand field coefficients in front of the irreducible spherical tensor operators T[combining circumflex]qk; B[combining right harpoon above]^T is the magnetic field vector defined in the same frame as ligand field; g is the g-tensor; 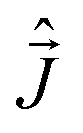vector of the x, y, z components of the total momentum operator;

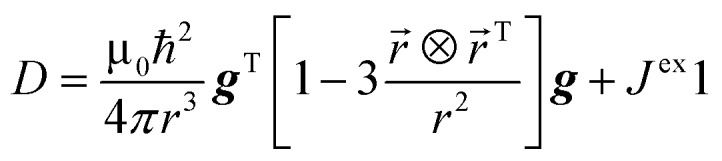4

is the matrix of dipolar interaction and isotropic exchange interaction between ions.80 The exchange interactions have been computed using the broken-symmetry approach as implemented in ORCA 4.0 (ref. 81) with B3LYP/def-TZVP method on X-Ray structures. The exchange coupling constant was computed using the Yamaguchi formalism.82

Conflicts of interest

There are no conflicts to declare.