Variational implicit-solvent predictions of the dry–wet transition pathways for ligand–receptor binding and unbinding kinetics

Significance

The kinetics of ligand–receptor (un)binding—how fast a ligand binds into and resides in a receptor—cannot be inferred solely from the binding affinity which describes the thermodynamic stability of the bound complex. A bottleneck in understanding such kinetics, which is critical to drug efficacy, lies in the modeling of the collective water fluctuations in apolar confinement. We develop a theoretical approach that couples a variational implicit-solvent model with the string method to describe the dry–wet transition pathways, which then serve as input for the ligand multistate Brownian dynamics. Without explicit descriptions of individual water molecules, our theory predicts the key thermodynamic and kinetic properties of unbinding and binding, the latter in quantitative agreement with explicit-water molecular dynamics simulations.

Abstract

Ligand–receptor binding and unbinding are fundamental biomolecular processes and particularly essential to drug efficacy. Environmental water fluctuations, however, impact the corresponding thermodynamics and kinetics and thereby challenge theoretical descriptions. Here, we devise a holistic, implicit-solvent, multimethod approach to predict the (un)binding kinetics for a generic ligand–pocket model. We use the variational implicit-solvent model (VISM) to calculate the solute–solvent interfacial structures and the corresponding free energies, and combine the VISM with the string method to obtain the minimum energy paths and transition states between the various metastable (“dry” and “wet”) hydration states. The resulting dry–wet transition rates are then used in a spatially dependent multistate continuous-time Markov chain Brownian dynamics simulation and the related Fokker–Planck equation calculations of the ligand stochastic motion, providing the mean first-passage times for binding and unbinding. We find the hydration transitions to significantly slow down the binding process, in semiquantitative agreement with existing explicit-water simulations, but significantly accelerate the unbinding process. Moreover, our methods allow the characterization of nonequilibrium hydration states of pocket and ligand during the ligand movement, for which we find substantial memory and hysteresis effects for binding vs. unbinding. Our study thus provides a significant step forward toward efficient, physics-based interpretation and predictions of the complex kinetics in realistic ligand–receptor systems.

The complex process of ligand–receptor binding and unbinding in an aqueous environment is fundamental to biological function. Understanding the thermodynamics and kinetics of such processes has far-reaching practical significance, particularly in rational drug design (1, 2). Water is a key player in ligand–receptor binding and unbinding and in molecular recognition in general (3, 4). In particular, it has been well established that hydrophobic interactions can drive the association and dissociation of biological molecules (5–8).

Hydration contributes significantly to the ligand–receptor binding free energy, determining the thermodynamic stability of the bound unit (9, 10). Recent experimental and theoretical studies have indicated that the kinetics of ligand–receptor binding and unbinding are crucial for drug effectiveness and efficacy (2, 11, 12). Often, a ligand binds to a hydrophobic pocket on the surface of a receptor molecule (13–16). Water molecules fluctuate around such an apolar pocket, leading to metastable “dry” or “wet” hydration states of the binding site, separated by an energetic barrier which is on the order of $k_{\mathrm{B}}T$ (17). Such a moderate energetic hurdle facilitates repeated condensation and evaporation of water in the pocket region, leading to large collective hydration fluctuations (18). In general, the dewetting of local regions generates strong hydrophobic forces in molecular association and dissociation (6, 7, 19, 20). In particular, it has been demonstrated that the dry–wet transitions are a precursor of the ligand–receptor binding and unbinding (17, 21, 22). Besides being the origin for the thermodynamically driven forces, water fluctuations also modify the friction and kinetics of associating hydrophobic molecules (23–27), slowing down the binding kinetics and giving rise to local non-Markovian effects (18, 27).

While water plays a critical role in molecular recognition, efficient modeling of water is rather challenging due to an overwhelming number of solvent degrees of freedom, many-body effects, and the multiscale nature of molecular interactions. Explicit-water molecular dynamics (MD) simulations have been the main tool in most of the existing studies of the kinetics of ligand–receptor binding and unbinding (18, 22, 25, 26, 28–33). While explicitly tracking water molecules, MD simulations are still limited to systems of relatively small sizes and events of relatively short timescales. In particular, slow and rare water fluctuations and large ligand residence times in the pocket still challenge the prediction of unbinding times.

In this work, we develop a holistic, multimethod, implicit-solvent approach to study the kinetics of ligand–receptor binding and unbinding in a generic pocket–ligand model exactly as studied previously by explicit-water MD simulations (18), focusing on the effect of solvent fluctuations and multiple hydration states on such processes.

Our approach is based on the variational implicit-solvent model (VISM) that we have developed in recent years (34–38). In VISM, one minimizes a solvation free-energy functional of solute–solvent interfaces to determine a stable equilibrium conformation and to provide an approximation of the solvation free energy. The functional couples the solute surface energy, solute–solvent van der Waals (vdW) dispersive interactions, and electrostatics. This theory resembles that of Lum–Chandler–Weeks (39) (cf. also refs. 40 and 41) and is different from the existing solvent-accessible surface (SAS)-type models. We have designed and implemented a robust level-set method to numerically minimize the VISM functional with arbitrary 3D geometry (36–38, 42).

Here, for our model ligand–pocket system, we use our level-set VISM to obtain different hydration states and their solvation free energies, and use the VISM-string method (43, 44) to find the minimum energy paths connecting such states and the corresponding transition rates. Such rates are then used in our continuous-time Markov chain Brownian dynamics simulations, and the related Fokker–Planck equation calculations, of the ligand stochastic motion to obtain the mean first-passage times for the ligand binding and unbinding. We compare our results with existing explicit-water MD simulations.

The Model Ligand–Receptor System.

The generic pocket–ligand model (45) consists of a hemispherical pocket and a methane-like molecule (Fig. 1A). The pocket, with the radius $R=8$ Å and centered at $\left(\mathrm{0,0,0}\right)$, is embedded in a rectangular wall, composed of apolar atoms aligned in a hexagonal close-packed grid of lattice constant 1.25 Å. The wall surface is oriented in the $xy$ plane. The ligand, a single neutral Lennard-Jones (LJ) sphere, is placed along the pocket symmetry axis, the $z$ axis, which is taken to be the reaction coordinate. Fig. 1 B–D depicts the cross-sections of all of the possible VISM surfaces, i.e., the stable solute–solvent interfaces separating the solute region ${\mathrm{\Omega }}_{\mathrm{m}}$ and solvent region ${\mathrm{\Omega }}_{\mathrm{w}}$, representing different hydration states for a fixed position of ligand.

Fig. 1.

(A) A schematic of the ligand (blue sphere), explicit water, and the pocket of a concave wall. (B) In 1s-dry, the VISM surface (blue line) is a single surface enclosing all of the wall atoms and also the ligand atom and hence a dry state of the pocket. (C) In 2s-dry, the VISM surface has 2 disjoint components, 1 enclosing all of the wall atoms with a dry pocket and 1 enclosing the ligand. (D) In 2s-wet, the VISM surface has 2 components, tightly wrapping up the wall and ligand, respectively, with no space for water and hence a wet pocket.

Results and Analysis

Multiple Hydration States and the Potential of Mean Force.

We use our level-set method to minimize the VISM solvation free-energy functional (Eq. 2 in Theory and Methods) and obtain a VISM surface. By choosing different initial solute–solvent interfaces, we obtain different VISM surfaces describing different hydration states (Fig. 1).

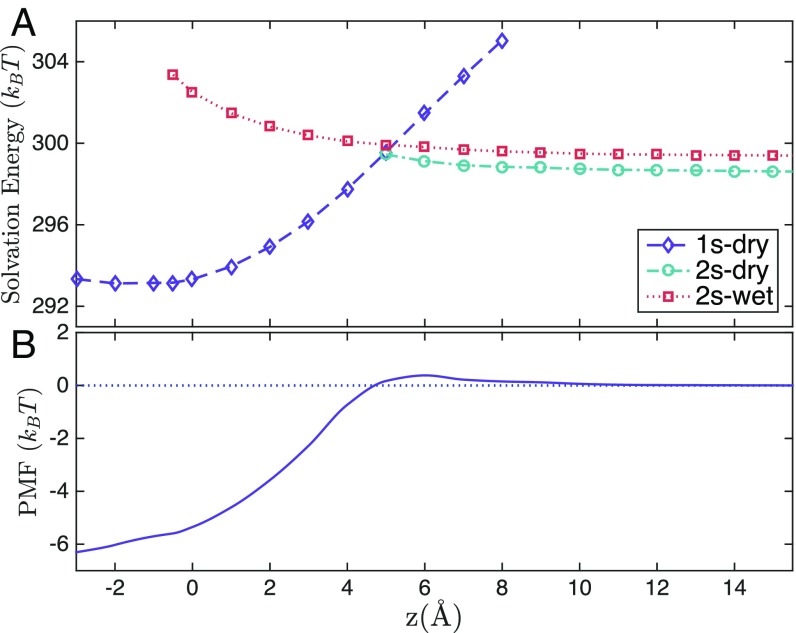
Fig. 2A shows the solvation free energies for different VISM surfaces against the reaction coordinate $z$. For $z<-0.5$ Å, there is only 1 VISM surface, 1s-dry (Fig. 1B). In addition to 1s-dry, a second VISM surface, 2s-wet, appears for $-0.5<z<5$ Å (Fig. 1D). For $5<z<8$ Å, there are 3 VISM surfaces. In addition to 1s-dry and 2s-wet, the third one is 2s-dry (Fig. 1C). Once the ligand is away from the pocket with $z>8$ Å, there are only 2 VISM surfaces: 2s-dry and 2s-wet.

Fig. 2.

(A) Solvation free energies of different VISM surfaces vs. the ligand location. (B) The equilibrium PMF.

Fig. 2B shows the equilibrium potential of mean force (PMF), defined as

$$V\left(z\right)=-k_{\mathrm{B}}T\ln \left(\sum _{\mathrm{\Gamma }\left(z\right)}{e}^{-G\left[\mathrm{\Gamma }\left(z\right)\right]/k_{\mathrm{B}}T}\right)+U_0\left(z\right)+V_{\infty },$$ [1]

where $\mathrm{\Gamma }\left(z\right)$ runs over all of the VISM surfaces with $G\left[\mathrm{\Gamma }\left(z\right)\right]$ the VISM solvation free energy at $\mathrm{\Gamma }\left(z\right)$, and $U_0\left(z\right)={\sum }_{{\mathbf{r}}_i}{U}_{\mathrm{L}\mathrm{J}}\left(|{\mathbf{r}}_i-{\mathbf{r}}_z|\right)$ with ${\mathbf{r}}_z$ the ligand position vector, ${\mathbf{r}}_i$ running through all of the wall atoms, and $U_{\mathrm{L}\mathrm{J}}\left(r\right)$ a 12–6 LJ potential. The constant $V_{\infty }$ is chosen so that $V\left(\infty \right)=0.$ The PMF agrees well with the result from MD simulations (17, 46, 47).

Dry–Wet Transition Paths and Energy Barriers.

At a fixed reaction coordinate $z$ with multiple hydration states, we use our level-set VISM coupled with the string method to calculate the minimum energy paths (MEPs) that connect these states and the corresponding transition states, energy barriers, and ultimately the transition rates. A string or path here consists of a family of solute–solvent interfaces, and each point of a string, which is an interface in our case, is called an image.

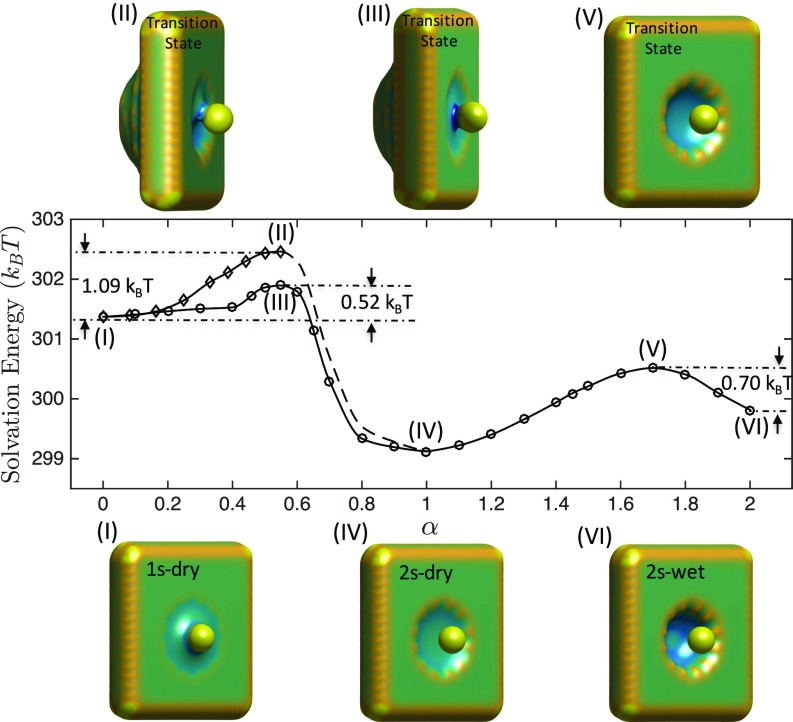
In Fig. 3, we display the solvation free energies of images on MEPs that connect the 3 hydration states, 1s-dry, 2s-dry, and 2s-wet, at $z=6$ Å. There are 2 MEPs connecting 1s-dry (marked I) and 2s-dry (marked IV). One of them passes through the axisymmetric transition state marked III, and the other passes through the axiasymmetric transition state marked II. Here, symmetry or asymmetry refers to that of the 3D conformation of the VISM surface. Energy barriers in the transition from the state 1s-dry to 2s-dry along the 2 transition paths are estimated to be $1.09\hspace{0.17em}{k}_{\mathrm{B}}T$ and $0.52\hspace{0.17em}{k}_{\mathrm{B}}T$, respectively. Only 1 MEP is found to connect 2s-dry (marked IV) and 2s-wet (marked VI), and the corresponding transition state (marked V) is also found. The MEP from 1s-dry to 2s-wet always passes through the state 2s-dry.

Fig. 3.

Solvation free energies of images on MEPs that connect the hydration states 1s-dry (I), 2s-dry (IV), and 2s-wet (VI) (shown at Bottom) with transition states (II), (III), and (V) (shown at Top) and the transition energy barriers for $z=6$ Å. In Middle plots, the horizontal axis is the string parameter $\alpha$.

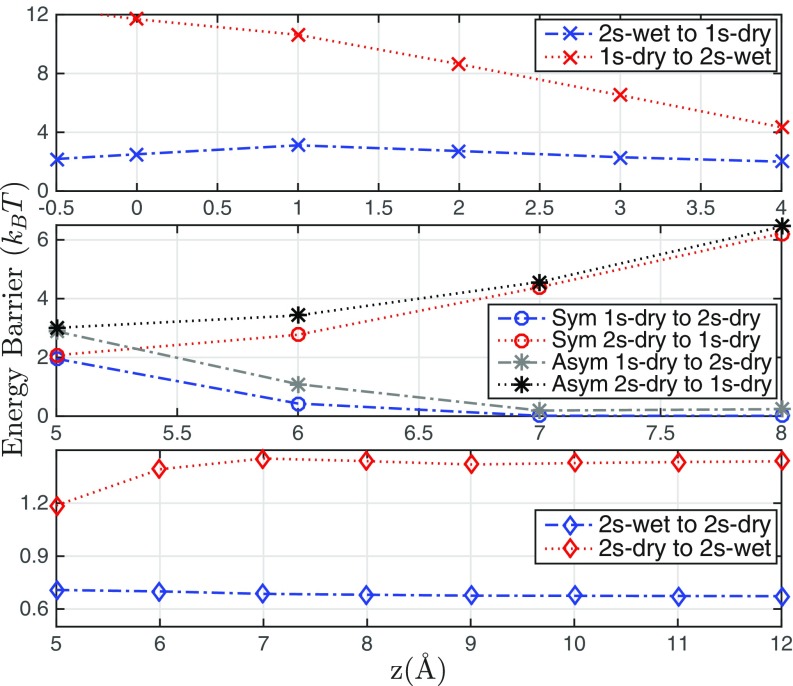
Fig. 4 summarizes all of the energy barriers in the transitions from one hydration state to another for each reaction coordinate $z.$ For $0\le z\le 4$ Å shown in Fig. 4, Top there are only 2 hydration states: 1s-dry and 2s-wet. The 1s-dry state has a lower free energy (Fig. 2A), and hence the barrier in the wetting transition from 1s-dry to 2s-wet (shown in red) is higher than that in the dewetting transition from 2s-wet to 1s-dry (shown in blue). The dewetting barrier first increases as the ligand approaches the entrance of the pocket (from $z=4$ to $z=1$ Å) and then decreases after the ligand enters the pocket (from $z=1$ to $z=-0.5$ Å). This is because the more attractive solute–solvent vdW interaction is lost in dewetting as the ligand–pocket distance reduces from $z=4$ to $z=1$ Å, and the decrease in interfacial energy outweighs the vdW contribution to the solvation free energy as the distance further reduces from $z=1$ to $z=-0.5$ Å. Our predictions agree well with those by the explicit-water MD simulations (17).

Fig. 4.

Transition energy barriers vs. the reaction coordinate $z$ with $-0.5\le z\le 4$ Å (Top) and $5\le z\le 12$ Å (Middle and Bottom). Sym stands for a MEP with an axisymmetric transition state and Asym stands for a MEP with an axiasymmetric transition state.

For $5\le z\le 8$ Å, there are 3 hydration states 1s-dry, 2s-wet, and 2s-dry (Fig. 2A). In Fig. 4, Middle we plot for $z$ in this range the energy barriers along the MEPs, both axisymmetric and axiasymmetric, connecting the 2 states 1s-dry and 2s-dry (Fig. 3). Note that, as the ligand approaches the pocket, the solute–solvent interfacial energy changes rapidly, and hence the barrier in the transition from 1s-dry to 2s-dry increases quickly, while the barrier in the reverse transition decreases quickly.

In Fig. 4, Bottom we plot energy barriers for transitions between the states 2s-dry and 2s-wet in the range $5\le z\le 12$ Å (Fig. 2A). As the ligand–pocket distance increases, the barrier for the wetting transition (marked red) first increases, since the newly created solvent region with attractive solute–solvent vdW interaction decreases. It then reaches a plateau after the distance is greater than 7 Å. The pocket dewetting barrier (marked blue) is slightly larger when the ligand is close to the pocket, since contributions of solute–solvent vdW interaction are lost during the pocket dewetting.

Kinetics of Binding and Unbinding.

We perform continuous-time Markov chain (CTMC) Brownian dynamics (BD) simulations and solve the related Fokker–Planck equation (FPE) calculations for the ligand stochastic motion with the pocket dry–wet fluctuations (Theory and Methods). For comparison, we also perform the usual BD simulations and FPE calculations without including such fluctuations.

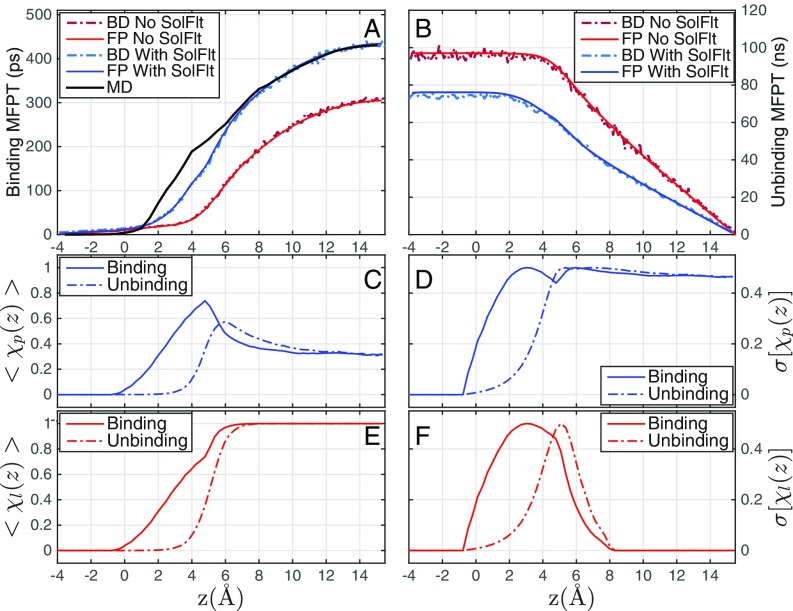
Fig. 5 A and B shows the mean first-passage times (MFPTs) for the binding and unbinding, respectively. Note that the BD simulations and FPE calculations agree with each other perfectly for both binding and unbinding, without and with the pocket dry–wet fluctuations, respectively. This validates mutually the accuracy of our numerical schemes. Note also that the binding/unbinding MFPT increases/decreases monotonically as the ligand–pocket distance increases, due to elongated/shortened ligand travel.

Fig. 5.

(A and B) The MFPT for (A) the binding of ligand that starts from $z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}=z$ and reaches the pocket at $z_{\mathrm{L}}=-4$ Å and (B) the unbinding of ligand that starts from $z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}=z$ and reaches $z_{\mathrm{R}}=15.5$ Å, predicted by BD simulations without (BD No SolFlt) and with (BD With SolFlt) the dry–wet fluctuations, and FPE calculations without (FP No SolFlt) and with (FP With SolFlt) the dry–wet fluctuations, respectively. Note that the time unit on the vertical axis in B is nanoseconds (ns) while that in A is picoseconds (ps). The MFPT obtained by explicit-water MD simulations (MD) (18) is also shown in A. (C–F) The mean values and SDs of the pocket and ligand hydration states ${\chi }_p\left(z\right)$ and ${\chi }_l\left(z\right)$, respectively, against the ligand location $z$ during the nonequilibrium binding process from the BD simulations starting at $z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}=6$ Å (C and E) and the unbinding process starting at $z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}=-2$ Å (D and F).

In Fig. 5A, we see that the MFPT for binding is very small if $z<-0.5$ Å. This is because the ligand diffusion constant $D_{\mathrm{i}\mathrm{n}}$ inside the pocket is large and the PMF is highly attractive (Fig. 2B). As the initial position $z$ increases from 0 Å to 5 Å, the difference between the 2 MFPTs with and without the pocket dry–wet fluctuations increases from nearly 0 ps to 100 ps. Such an increasing difference results from the existence of the hydration state 2s-wet in this range, and the solvation free energy of this state increases as the ligand moves from $z=5$ Å to $z=0$ Å (Fig. 2A). The pocket dry–wet fluctuations thus decelerate considerably the ligand–pocket association. Such deceleration has been explained by the reduced diffusivity of the ligand in the vicinity of pocket entrance due to the slow solvent fluctuations (18).

Our predictions of the MFPT for binding, with the dry-wet fluctuations included, agree very well with the explicit-water MD simulations (18), improving significantly over those without such fluctuations. Note that our model predicts somewhat shorter binding times than the MD simulations for $1<z<6$ Å. In this region, the hydration fluctuations are maximal, and this visible but relatively small (compared with the MFPT from the farthest distance) discrepancy reflects some of the approximations of our implicit-solvent theory and the model reduction on just a few states.

Fig. 5B shows that the timescale for unbinding is significantly larger than that for the binding, by nearly 3 orders of magnitude. Without the pocket dry–wet fluctuations, the unbinding MFPT is constant for $z<4$ Å and decreases linearly for $z>4$ Å. Note that the MFPT for binding in this case also starts to increase significantly at $z=4$ Å (Fig. 5A). With the pocket dry–wet fluctuations, the unbinding MFPT is much smaller, since the solvation free energy of the 2s-wet state is higher when the ligand is closer to the pocket (Fig. 2A), favoring the ligand unbinding. In this case, the MFPT remains constant up to $z=2$ Å and then decays almost linearly. This suggests that the wetting transitions occur if $z>2$ Å. Note from Fig. 5A that the binding MFPT starts increasing rapidly also around $z=2$ Å.

We now study the interesting hydration of the pocket and ligand individually during the nonequilibrium binding/unbinding processes. For this, we define a pocket hydration parameter to be ${\chi }_{\mathrm{p}}\left(z\right)=0$ or 1 if the pocket is dry or wet, respectively. Analogously, we set for the ligand ${\chi }_{\mathrm{l}}\left(z\right)=0$ or 1 if the ligand is dry or wet, respectively. The values 0 and 1 of these ligand-position–dependent random variables ${\chi }_{\mathrm{p}}\left(z\right)$ and ${\chi }_l\left(z\right)$ are defined by the 3 hydration states 1s-dry, 2s-dry, and 2s-wet (Fig. 1 B–D) as follows:

• ${\chi }_{\mathrm{p}}\left(z\right)=0$ and ${\chi }_l\left(z\right)=0$ for a 1s-dry VISM surface;

• ${\chi }_{\mathrm{p}}\left(z\right)=0$ and ${\chi }_l\left(z\right)=1$ for a 2s-dry VISM surface; and

• ${\chi }_{\mathrm{p}}\left(z\right)=1$ and ${\chi }_l\left(z\right)=1$ for a 2s-wet VISM surface.

Fig. 5 C–F shows the mean values, $⟨{\chi }_{\mathrm{p}}\left(z\right)⟩$ and $⟨{\chi }_{\mathrm{l}}\left(z\right)⟩$, and the SDs, $\sigma \left[{\chi }_{\mathrm{p}}\left(z\right)\right]$ and $\sigma \left[{\chi }_l\left(z\right)\right],$ during the binding and the unbinding processes, respectively.

When the ligand is far away, there are only 2 VISM surfaces, 2s-dry and 2s-wet (Fig. 2A). For such a case, our BD simulations predict the probability 32% of a wet pocket (i.e., ${\chi }_p=0.32$ for large $z$) in the binding and unbinding processes. This is perfectly consistent with the equilibrium probability $e^{-G\left[{\mathrm{\Gamma }}_{\mathrm{2}\mathrm{s}-\mathrm{w}\mathrm{e}\mathrm{t}}\right]/k_{\mathrm{B}}T}/\left(e^{-G\left[{\mathrm{\Gamma }}_{\mathrm{2}\mathrm{s}-\mathrm{d}\mathrm{r}\mathrm{y}}\right]/k_{\mathrm{B}}T}+e^{-G\left[{\mathrm{\Gamma }}_{\mathrm{2}\mathrm{s}-\mathrm{w}\mathrm{e}\mathrm{t}}\right]/k_{\mathrm{B}}T}\right)$ predicted by our VISM theory. We observe that the pocket hydration peaks at the entrance of the pocket in binding, agreeing well with MD simulations (17, 18), where it was argued that stronger pocket hydration is induced by the penetration of the ligand solvation shell. When the ligand enters the pocket, the latter becomes dry as anticipated.

In comparison, the maximum pocket hydration for unbinding is shifted a bit away from the pocket. This kinetic asymmetry or “translational mismatch” can be explained as well by the asymmetric hydration states of the ligand (Fig. 5E), which exits the pocket without a complete solvation shell. This behavior is reminiscent of a hysteresis; that is, the hydration states during the ligand passage depend on the history of the ligand, i.e., where it comes from.

The SDs of pocket hydration shown in Fig. 5D depict that the dry–wet fluctuations have local maxima close to the pocket entrance ($z\simeq 3-5$ Å) and behave also significantly differently for binding and unbinding. The corresponding SDs of ligand hydration shown in Fig. 5F show massively unstable hydration (i.e., large peaks) close to the pocket entrance, while inside and far away from the pocket the fluctuations are 0, indicating a very stable (de)hydration state. Again the peaks are at different locations for binding vs. unbinding, reflecting the hysteresis and memory of dry–wet transitions during ligand passage.

Conclusions

We have developed an implicit-solvent approach, coupling our VISM, the string method, and multistate CTMC BD simulations, for studying the kinetics of ligand–receptor binding and unbinding, particularly the influence of collective solvent fluctuations on such processes. Without any explicit descriptions of individual water molecules, our predictions of the MFPT for the binding process, which is decelerated by the solvent fluctuations around the pocket, agree very well with the less efficient explicit-water MD simulations. Moreover, we find surprisingly that the solvent fluctuations accelerate the ligand unbinding from the pocket, which involves a much larger timescale and is thus more challenging for explicit-water MD simulations (26, 30). Importantly, our implicit-solvent approach indicates that the water effects are controlled by a few key physical parameters and mechanisms, such as polymodal nanocapillarity based on surface tension of the solute–solvent interface and the coupling of the random interface forces to the ligand’s diffusive motion.

Our approach provides a promising direction in efficiently probing the kinetics, and thermodynamics, of the association and dissociation of complex ligand–receptor systems, which have been studied mostly using enhanced sampling techniques (18, 25, 26, 28, 30, 32). Our next step is to extend our approach for more realistic systems with general reaction coordinates and different techniques for sampling transition paths (48, 49). Our VISM can treat efficiently the electrostatic interactions using the Poisson–Boltzmann theory (38). To account for the flexibility of the ligand and receptor in their binding and unbinding, we shall expand our solvation model to include the solute molecular mechanical interactions (50).

Theory and Methods

VISM.

We consider the solvation of solute molecules, with all of the solute atomic positions ${\mathbf{r}}_1,\dots ,{\mathbf{r}}_N$, in an aqueous solvent that is treated implicitly as a continuum. (For our model ligand–pocket system, the solute atoms include those of the concave wall and the single atom of the ligand [Fig. 1].) A solute–solvent interface $\mathrm{\Gamma }$ is a closed surface that encloses all of the solute atoms but no solvent molecules. The interior and exterior of $\mathrm{\Gamma }$ are the solute and solvent regions, denoted ${\mathrm{\Omega }}_{\mathrm{m}}$ and ${\mathrm{\Omega }}_{\mathrm{w}}$, respectively. We introduce the VISM solvation free-energy functional (34, 35)

$$G\left[\mathrm{\Gamma }\right]=\mathrm{\Delta }P\hspace{0.17em}\text{vol}\hspace{0.17em}\left({\mathrm{\Omega }}_{\mathrm{m}}\right)+{\int }_{\mathrm{\Gamma }}\gamma \hspace{0.17em}dS+{\rho }_0{\int }_{{\mathrm{\Omega }}_{\mathrm{w}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}U\left(\mathbf{r}\right)\hspace{0.17em}dV+G_{\mathrm{e}}\left[\mathrm{\Gamma }\right].$$ [2]

Here, $\mathrm{\Delta }P$ is the difference of pressures across the interface $\mathrm{\Gamma }$, $\gamma$ is the solute–solvent interface surface tension, ${\rho }_0$ is the bulk solvent (i.e., water) density, and $U\left(\mathbf{r}\right)={\sum }_{i=1}^N{U}_i\left(|\mathbf{r}-{\mathbf{r}}_i|\right)$ with each $U_i$ a standard 12–6 LJ potential. We take $\gamma ={\gamma }_0\left(1-2\tau H\right),$ where ${\gamma }_0$ is the surface tension for a planar interface, $\tau$ is the curvature correction coefficient often known as the Tolman length (51), and $H$ is the local mean curvature. The last term $G_{\mathrm{e}}\left[\mathrm{\Gamma }\right]$ is the electrostatic part of the solvation free energy, which we do not include in this study.

Minimizing the functional Eq. 2 among all of the solute–solvent interfaces $\mathrm{\Gamma }$ determines a stable, equilibrium, solute–solvent interface, called a VISM surface, and the corresponding solvation free energy. A VISM surface is termed dry, representing a dry hydration state, if it loosely wraps up all of the solute atoms with enough space for a few solvent molecules, or wet, representing a wet hydration state, if it tightly wraps up all of the solute atoms without extra space for a solvent molecule.

Implementation by the Level-Set Method.

Beginning with an initially guessed solute–solvent interface, our level-set method evolves the interface step by step in the steepest descent direction until a VISM surface is reached. Different initial surfaces may lead to different final VISM surfaces. See SI Appendix for more details of implementation.

The Level-Set VISM-String Method for MEPs.

Let us fix all of the solute atomic positions and assume that ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ are 2 VISM surfaces (e.g., dry and wet surfaces). We apply the string method (43, 44) to find a MEP that connects ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$. A string or path here is a family of solute–solvent interfaces ${\left\{{\mathrm{\Gamma }}_{\alpha }\right\}}_{\alpha \in \left[\mathrm{0,1}\right]}$ that connects the 2 states ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$. Such a string is a MEP, if it is orthogonal to the level surfaces of the VISM free-energy functional. To find a MEP connecting ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1,$ we select some initial images (i.e., points of a string) and then update them iteratively to reach a MEP. Different initial images may lead to different MEPs. Once a MEP is found, we can then find a saddle point on the MEP. Alternatively, we can fix 1 of the VISM surfaces, select some initial images, and allow the last image to climb up to reach a saddle point, and then find the MEP connecting the 2 VISM surfaces passing the saddle point. We refer to SI Appendix for more details on our implementation of the method.

Consider now our ligand–pocket system (Fig. 1). For any reaction coordinate $z,$ we label all of the 3 hydration states 1s-dry, 2s-dry, and 2s-wet (Fig. 1) as the states 0, 1, and 2, respectively. We define for each $i\in \left\{\mathrm{0,1,2}\right\}$ the potential

$$V_i\left(z\right)=G_i\left(z\right)+U_0\left(z\right),$$ [3]

where $G_i\left(z\right)$ is the solvation free energy of the $i$th state at $z$ (Fig 2A) and $U_0\left(z\right)$ is the ligand–pocket vdW interaction potential defined below Eq. 1. We set $V_i\left(z\right)=0$ if the $i$th state does not exist at $z$.

With the energy barriers summarized in Fig. 4, we can calculate for each $z$ the rate $R_{ij}=R_{ij}\left(z\right)$ of the transition from one state $i$ to another $j.$ If a MEP from $i$ to $j$ passes through another state $k$ (Fig. 3), then we set $R_{ij}\left(z\right)=0.$ If there is only 1 MEP connecting $i$ and $j$ (e.g., $z<4$ in Fig. 2), then $R_{ij}=R_0{e}^{-B_{ij}\left(z\right)/k_{\mathrm{B}}T}$ with $B_{ij}\left(z\right)$ the energy barrier from $i$ to $j$ and $R_0$ a constant prefactor, describing the intrinsic timescale of water dynamics in the pocket. Finally, if there are 2 MEPs (axisymmetric and axiasymmetric) connecting $i$ and $j$, we use the same formula but with $B_{ij}$ an effective barrier. For instance, consider $i$ and $j$ the states I and IV in Fig. 3, respectively. The 2 transition states are II and III, respectively. We set $B_{ij}\left(z\right)=B_{\mathrm{I},\mathrm{I}\mathrm{V}}\left(z\right)=p\left(G_{\mathrm{I}\mathrm{I}}-G_{\mathrm{I}}\right)+\left(1-p\right)\left(G_{\mathrm{I}\mathrm{I}\mathrm{I}}-G_{\mathrm{I}}\right)$, where $p=e^{-\left(G_{\mathrm{I}\mathrm{I}}-G_{\mathrm{I}}\right)/k_{\mathrm{B}}T}/\left(e^{-\left(G_{\mathrm{I}\mathrm{I}}-G_{\mathrm{I}}\right)/k_{\mathrm{B}}T}+e^{-\left(G_{\mathrm{I}\mathrm{I}\mathrm{I}}-G_{\mathrm{I}}\right)/k_{\mathrm{B}}T}\right)$ and $G_A$ is the VISM solvation free energy at state $A\in \left\{\mathrm{I},\mathrm{I}\mathrm{I},\mathrm{I}\mathrm{I}\mathrm{I}\right\}$. To determine the prefactor $R_0$, we calculate the equilibrium (i.e., the large $z$ limit) energy barriers $B_{\mathrm{d}\mathrm{w}}$ and $B_{\mathrm{w}\mathrm{d}}$ in the pocket dry–wet and wet–dry transitions, respectively, and equate ${\left[R_0\left(e^{-B_{\mathrm{d}\mathrm{w}}/k_{\mathrm{B}}T}+e^{-B_{\mathrm{w}\mathrm{d}}/k_{\mathrm{B}}T}\right)\right]}^{-1}$ with the timescale for the relaxation of water fluctuation of 10 ps as predicted by explicit-water MD simulations (18). See SI Appendix for discussions on the sensitivity of the results on $R_0.$

CTMC BD Simulations and the MFPT.

To include explicitly the dry–wet fluctuations, we introduce a position-dependent, multistate, random variable $\eta =\eta \left(z\right)$: $\eta \left(z\right)=i\hspace{0.17em}\left(i\in \left\{\mathrm{0,1,2}\right\}\right)$ if the system is in the $i$th hydration state when the ligand is located at $z$, with the transition rates $R_{ij}\left(z\right)$ given above. We define the potential $V_{\mathrm{fl}\mathrm{u}\mathrm{c}}\left(\eta ,z\right)=V_i\left(z\right)$ (Eq. 3) if $\eta \left(z\right)=i$ (52). The random position $z=z\left(t\right)=z_t$ of the ligand is now determined by our CTMC BD simulations in which we solve the stochastic differential equation

$$d{z}_t=\left[-\frac{D\left(z_t\right)}{k_{\mathrm{B}}T}\frac{\partial V_{\mathrm{fl}\mathrm{u}\mathrm{c}}\left(\eta \left(z_t\right),z_t\right)}{\partial z}+D\prime \left(z_t\right)\right]dt+\sqrt{2D\left(z_t\right)}\hspace{0.17em}d{\xi }_t.$$

Here, the partial derivative of $V_{\mathrm{fl}\mathrm{u}\mathrm{c}}$ is with respect to its second variable, $D\left(z\right)$ is an effective diffusion coefficient that smoothly interpolates the diffusion coefficients $D_{\mathrm{i}\mathrm{n}}$ and $D_{\mathrm{o}\mathrm{u}\mathrm{t}}$ inside and outside the pocket, respectively, and ${\xi }_t$ is the standard Brownian motion. Solutions to this equation are constrained by $z_t\in \left[z_{\mathrm{L}},z_{\mathrm{R}}\right]$ for some $z_{\mathrm{L}}$ and $z_{\mathrm{R}}.$ For the simulation of a binding process, we reset the value of $z_t$ to be $2z_{\mathrm{R}}-z_t$ if $z_t\ge z_{\mathrm{R}}$, and we stop the simulation if $z_t\le z_{\mathrm{L}}$. For the simulation of an unbinding process, we reset the value of $z\left(t\right)$ to be $z_{\mathrm{L}}$ if $z_t\le z_{\mathrm{L}}$, and we stop the simulation if $z_t\ge z_{\mathrm{R}}.$ The distribution of $\eta \left(z_0\right)$ for an initial ligand position $z_0$ is set based on the equilibrium probabilities $e^{-G_i/k_{\mathrm{B}}T}/{\sum }_{j=0}^2{e}^{-G_j/k_{\mathrm{B}}T}\hspace{0.17em}\left(i=\mathrm{0,1,2}\right),$ where $G_i$ is the solvation free energy of the $i$th hydration state at $z_0.$

We run our CTMC BD simulation for the ligand starting at a position $z_0=z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}$ and record the time at which the ligand reaches $z_{\mathrm{L}}$ (or $z_{\mathrm{R}}$) for the first time for a binding (or unbinding) simulation. We run simulations for $\mathrm{3,000}$ times and average these times to obtain the corresponding MFPTs.

FPEs and the MFPT.

The probability densities $P_i=P_i\left(z,t\right)$ for the ligand at location $z$ at time $t$ with the system in the $i$th hydration state are determined by the generalized FPEs (25, 52)

$$\begin{array}{cc}\hfill \frac{\partial P_i}{\partial t}& =\frac{\partial }{\partial z}\left\{D\left(z\right)\left[\frac{\partial P_i}{\partial z}+\frac{1}{k_{\mathrm{B}}T}{V}_i^{\prime }\left(z\right)P_i\right]\right\}\hfill \\ \hfill & +\sum _{0\le j\le 2,\hspace{0.17em}j/=i}{R}_{ji}\left(z\right)P_j-\left(\hspace{0.17em}\sum _{0\le j\le 2,\hspace{0.17em}j/=i}{R}_{ij}\left(z\right)\right)P_i\hfill \end{array}$$

for $i=\mathrm{0,1,2},$ where $V_i$ is defined in Eq. 3. These equations are solved for $z_{\mathrm{L}}<z<z_{\mathrm{R}},$ with the boundary conditions $P_i\left(z_{\mathrm{L}},t\right)=0$ and ${\partial }_z{P}_i\left(z_{\mathrm{R}},t\right)=0$ for binding, and ${\partial }_z{P}_i\left(z_{\mathrm{L}},t\right)+\left(1/k_{\mathrm{B}}T\right)V_i^{\prime }\left(z_L\right)P_i\left(z_{\mathrm{L}},t\right)=0$ and $P_i\left(z_{\mathrm{R}},t\right)=0$ for unbinding, respectively. The initial conditions are $P_i\left(z,0\right)=\delta \left(z-z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}\right)$ if the ligand is initially at $z_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}}.$ We obtain the MFPT as the double integral of ${\sum }_{i=0}^2{P}_i\left(z,t\right)$ over $\left(z,t\right)\in \left[z_{\mathrm{L}},z_{\mathrm{R}}\right]\times \left[0,\infty \right).$

Parameters.

We set the temperature $T=298$ K, bulk water density ${\rho }_0=0.033\hspace{0.17em}{\text{Å}}^{-3}$, the solute–water surface tension constant ${\gamma }_0=0.143\hspace{0.17em}{k}_{\mathrm{B}}T/{\text{Å}}^2$ ($k_{\mathrm{B}}$ is the Boltzmann constant), and the Tolman length $\tau =0.8$ Å. We set $\mathrm{\Delta }P\text{vol}\hspace{0.17em}\left({\mathrm{\Omega }}_{\mathrm{m}}\right)=0$ as it is relatively very small. The LJ parameters for the wall particles, ligand, and water are ${\epsilon }_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}=0.000967\hspace{0.17em}{k}_{\mathrm{B}}T$ and ${\sigma }_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}=4.152$ Å, ${\epsilon }_{\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{a}\mathrm{n}\mathrm{d}}=0.5\hspace{0.17em}{k}_{\mathrm{B}}T$ and ${\sigma }_{\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{a}\mathrm{n}\mathrm{d}}=3.73$ Å, and ${\epsilon }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=0.26\hspace{0.17em}{k}_{\mathrm{B}}T$ and ${\sigma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=3.154$ Å, respectively. The interaction LJ parameters are determined by the Lorentz–Berthelot mixing rules. The prefactor $R_0=0.13$ ps⁻¹. The diffusion constants are $D_{\mathrm{o}\mathrm{u}\mathrm{t}}=0.26\hspace{0.17em}{\text{Å}}^2$/ps (18) and $D_{\mathrm{i}\mathrm{n}}=1\hspace{0.17em}{\text{Å}}^2$/ps. The cutoff position distinguishing the inside and outside of the pocket is $z_{\mathrm{c}}=-0.5$ Å. BD simulations and FPE calculations are done for $z_{\mathrm{L}}\le z\le z_{\mathrm{R}}$ with $z_{\mathrm{L}}=-4$ Å and $z_{\mathrm{R}}=15.5$ Å.