Significance
Modeling single-neuron dynamics is the first step to quantitatively understand brain computation. Yet, the existing point neuron models fail to capture dendritic effects, which are crucial for neuronal information processing. We derive an effective point neuron model, which incorporates an additional synaptic integration current arising from the nonlinear interaction between synaptic currents across spatial dendrites. Our model captures the somatic voltage response of a neuron with complex dendrites and is capable of performing rich dendritic computations. Besides its computational efficiency in simulations, our model suggests reexamination of previous studies involving the decomposition of excitatory and inhibitory synaptic inputs based on the existing point neuron framework, e.g., the inhibition is often underestimated in experiment.
Keywords: dendritic computation, synaptic current, synaptic integration, single-neuron dynamics, point neuron model
Abstract
Complex dendrites in general present formidable challenges to understanding neuronal information processing. To circumvent the difficulty, a prevalent viewpoint simplifies the neuronal morphology as a point representing the soma, and the excitatory and inhibitory synaptic currents originated from the dendrites are treated as linearly summed at the soma. Despite its extensive applications, the validity of the synaptic current description remains unclear, and the existing point neuron framework fails to characterize the spatiotemporal aspects of dendritic integration supporting specific computations. Using electrophysiological experiments, realistic neuronal simulations, and theoretical analyses, we demonstrate that the traditional assumption of linear summation of synaptic currents is oversimplified and underestimates the inhibition effect. We then derive a form of synaptic integration current within the point neuron framework to capture dendritic effects. In the derived form, the interaction between each pair of synaptic inputs on the dendrites can be reliably parameterized by a single coefficient, suggesting the inherent low-dimensional structure of dendritic integration. We further generalize the form of synaptic integration current to capture the spatiotemporal interactions among multiple synaptic inputs and show that a point neuron model with the synaptic integration current incorporated possesses the computational ability of a spatial neuron with dendrites, including direction selectivity, coincidence detection, logical operation, and a bilinear dendritic integration rule discovered in experiment. Our work amends the modeling of synaptic inputs and improves the computational power of a modeling neuron within the point neuron framework.
A single neuron performs extensive computations through active dendrites with rich biophysical properties and morphological structures (1, 2). In general, it is difficult to understand information processing in a neuron when receiving broadly distributed synaptic activities on its dendrites. Despite the complexity of dendrites, the information is presumably encoded via action potentials generated at the soma of a neuron. Therefore, for a large set of issues regarding neuronal information coding, one usually simplifies a spatial neuron as a single point representing its soma with the membrane potential dynamics modeled as a resistance–capacitance circuit (3, 4),
| [1] |
where is the membrane capacitance and is the membrane potential at the soma. Here, is the intrinsic ionic current, and is the synaptic current. By modeling different , one can obtain a class of point neuron models, such as the leaky integrate-and-fire neuron and the Hodgkin–Huxley neuron (5). For the synaptic current , in general, the integration of all individual synaptic inputs originated from dendrites is phenomenologically incorporated into a linear summation of 2 effective excitatory (E) and inhibitory (I) synaptic currents arriving at the soma, that is,
| [2] |
where and are the effective E and I synaptic conductances at the soma, respectively; and and are the E and I reversal potentials, respectively.
Point neuron models with synaptic current taking the form of Eq. 2 have been extensively applied to both experimental and theoretical studies, including synaptic current decomposition (6, 7), synaptic conductance estimation (8–10), dynamic clamp stimulation (11, 12), and neuronal network dynamics modeling (13–20), etc. Despite the simplicity of the point neuron model in analysis and simulation, various important questions remain to be addressed. For instance, do the E and I synaptic currents arriving at the soma of a spatial neuron with dendrites follow a linear summation as described in Eq. 2? Can the point neuron model reflect dendritic integration effects and implement dendritic computations? If not, how do we establish a point neuron model to capture the essence of dendritic functions?
Results
Integration of E and I Synaptic Currents Revealed in Electrophysiological Experiments.
We first investigate these questions in a CA1 pyramidal neuron of rat hippocampal slices. The whole-cell recording is made from the soma of the pyramidal neuron with sampling frequency 100 kHz, and fluorescent dye Alexa Fluor 488 is loaded into the neuron via the recording pipette to visualize the dendritic tree (Fig. 1A). Microiontophoretic applications of E transmitter glutamate and I transmitter -aminobutyric acid (GABA) at the apical dendrite induce rapid membrane depolarizations and hyperpolarizations, respectively, with kinetics similar to those of natural excitatory postsynaptic potentials (EPSPs) and inhibitory postsynaptic potentials (IPSPs) elicited by extracellular electrical stimulation in the CA1 region, respectively (Fig. 1B) (21). For convenience, these iontophoretic responses are referred to hereafter as EPSPs and IPSPs. To assess the validity of the synaptic current modeling (Eq. 2), we first need to determine the intrinsic ionic current and the passive parameters in the point neuron description of this pyramidal neuron (Eq. 1). Early experiments demonstrate that, within the subthreshold regime, the dynamics of the somatic membrane potential of a pyramidal neuron can be described as a leaky integrator (22, 23). Therefore, in the absence of action potentials, the ionic current can be well characterized as , where is the resting potential about −60 mV measured from the soma of the pyramidal neuron. The passive parameters are determined as nS and pF by giving a hyperpolarizing step current −50 pA at the soma of the pyramidal neuron. By convention, we rescale the leak conductance and the capacitance by dividing the estimated area of the neuron to obtain and .
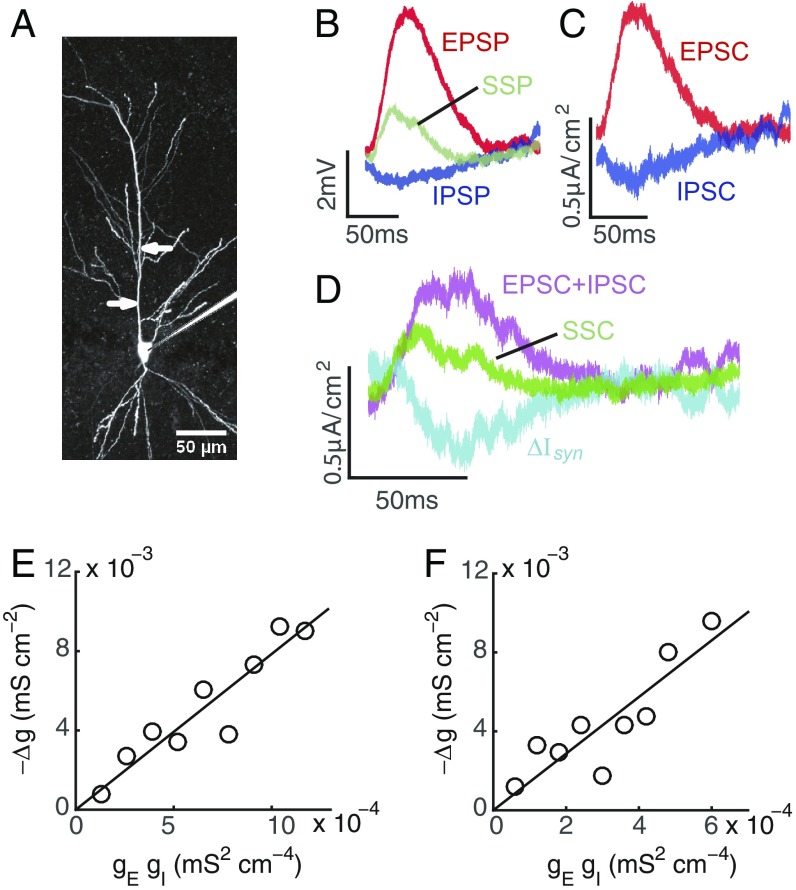
Fig. 1.
Experimental measurement of the bilinear conductance relation for a pair of E and I inputs. (A) Image of a CA1 pyramidal neuron. Arrows indicate pipettes for iontophoresis of glutamate and GABA at about 100 and 50 m from soma, respectively. (Scale bar: 50 m.) (B) A set of individual EPSP, individual IPSP, and SSP induced by both E and I inputs recorded in the experiment. A simple moving average with time window of 5 ms is applied to smooth each trace. (C) Constructed EPSC and IPSC using the SSP and the E and I conductances estimated from the EPSP and IPSP in B. (D) The SSC estimated from the SSP in B, the linear sum of the constructed EPSC and IPSC in C, and the difference between them denoted as . (E) The bilinear relation between and the multiplication of and at the time when the EPSP reaches its peak value. The E and I inputs are given simultaneously. Line indicates linear fit (slope, k, = 0.87). (F) The same as E except that the I input is given 20 ms preceded to the E input. Line indicates linear fit (slope, k, = 0.76). In E and F, by varying the E and I input strengths, the amplitude of EPSP ranges from 1 to 8 mV, and the amplitude of IPSP ranges from −1 to −3 mV. For the purpose of denoising, we first measure values of , , and for each set of EPSP, IPSP, and SSP; then, we construct a scatterplot of vs. , and finally, we divide the range of into 9 bins and average all of the data points within each bin. In addition, similar results can be obtained by replacing moving average with low-pass filtering, such as the elliptic filter.
We next examine whether the E and I synaptic currents follow a linear summation as described in Eq. 2 when the pyramidal neuron receives synaptic inputs from its dendrites. In the experiment, when an E input is elicited by an iontophoretic pipette placed at the dendritic trunk m away from the soma, an EPSP denoted as is recorded at the soma. To eliminate the numerical error when taking the temporal derivative of the EPSP, we smooth the EPSP trace by performing simple moving average with time window 5 ms. Using the smoothed EPSP (Fig. 1B), the corresponding effective excitatory postsynaptic current (EPSC) denoted as is derived based on the form of the point neuron model (Eq. 1), that is, . Similarly, when an I input is elicited by an iontophoretic pipette placed at the dendritic trunk m away from the soma, an IPSP denoted as is recorded at the soma and smoothed by simple moving average (Fig. 1B), and the corresponding effective inhibitory postsynaptic current (IPSC) denoted as is derived, that is, . Using the information of the EPSC and the IPSC, we further determine the effective E and I conductances at the soma as and , respectively, with the E reversal potential mV and the I reversal potential mV measured from the experiment.
When both the E and I inputs are elicited simultaneously with the input strengths and locations the same as given individually, a summed somatic potential (SSP) denoted as is recorded at the soma and smoothed by simple moving average (Fig. 1B), and the corresponding summed somatic current (SSC) denoted as is derived as . Based on the synaptic current description (Eq. 2) in the point neuron model, the SSC is presumably made of the linear summation of the E and I synaptic currents, that is, . However, by constructing the E and I synaptic currents, i.e., and , using the resolved conductances and and the postsynaptic potential (Fig. 1C), the SSC is found to be significantly different from instead of equal to the linear summation of the E and I synaptic currents (Fig. 1D). This fact demonstrates that the synaptic current description (Eq. 2) is insufficient to characterize the synaptic current arriving at the soma as a result of dendritic integration.
To analyze the integration of synaptic currents quantitatively, we denote the difference between the SSC and the linear sum of the EPSC and the IPSC as the synaptic integration current , that is, . If we cast this integration current in the form of Ohm’s law as with defined as the integration conductance, by randomly varying the strengths of the E and I synaptic inputs with their input locations fixed, the integration conductance is found to obey a bilinear rule throughout the response period until or vanishes (i.e., , where is the proportional coefficient independent of the input strengths but dependent of time). Note that, when the synaptic integration current is cast in the form of Ohm’s law, the reversal potential here is set to be the E reversal potential . We point out that the bilinear relation of the conductances remains valid when a different value of reversal potential is chosen (SI Appendix, Fig. S1), which will be further discussed in Discussion. The bilinear relation at a particular time point around the peak of the EPSP is illustrated in Fig. 1E (with coefficient of determination ). In addition, the bilinear relation remains valid even when there is a time delay between the E and I input arrival times. A particular case of the bilinear relation is shown in Fig. 1F () in which the I input is elicited 20 ms earlier than the E input. The proportional coefficients in both the concurrent and nonconcurrent inputs cases are not identical, indicating that is sensitive to input arrival time difference. Therefore, from our experiment, the synaptic current description (Eq. 2) in the point neuron framework should be modified to incorporate the synaptic integration current , and the corresponding integration conductance follows a bilinear rule with the proportional coefficient independent of input strengths but dependent of time. For the ease of discussion, we refer to as the integration coefficient.
Integration of E and I Synaptic Currents Revealed in Realistic Neuron Simulations.
To further confirm the existence and the structure of the synaptic integration current, we perform realistic neuron simulations in which the time derivatives of voltage can be precisely obtained to estimate the conductance values accurately. Here, a hippocampal CA1 pyramidal neuron model is built with a complex dendritic morphology (Fig. 2A) and active ionic channels (details of the model are in Materials and Methods). The E -amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor and I receptor are implemented on the dendrites of the neuron with kinetics consistent with experimental recordings (21). The resting and reversal potentials are set as , , and mV. Similar to the experimental procedure, we first determine the passive parameters in the point neuron description of the pyramidal neuron model by injecting a step current at the soma of the neuron: and . Then, in the simulation of the neuron model, an EPSP or an IPSP is measured at the soma (Fig. 2B) after eliciting an individual E synaptic input on the dendrite about m away from the soma or an individual I synaptic input about m away from the soma, respectively. The effective E and I conductances at the soma and are determined from the measured EPSP and IPSP, respectively. The neuron is then stimulated given both the E and I synaptic inputs simultaneously with the input strengths and input locations the same as given individually; an SSP is measured at the soma of the neuron, and the corresponding SSC is calculated. Consistent with our experimental observations, after constructing the EPSC and IPSC (Fig. 2C) using the E and I conductances and the SSP, the SSC is found to be significantly different from the linear summation of the constructed EPSC and IPSC (Fig. 2D). This indicates the existence of the synaptic integration current and challenges again the validity of the synaptic current form (Eq. 2) in the point neuron framework.
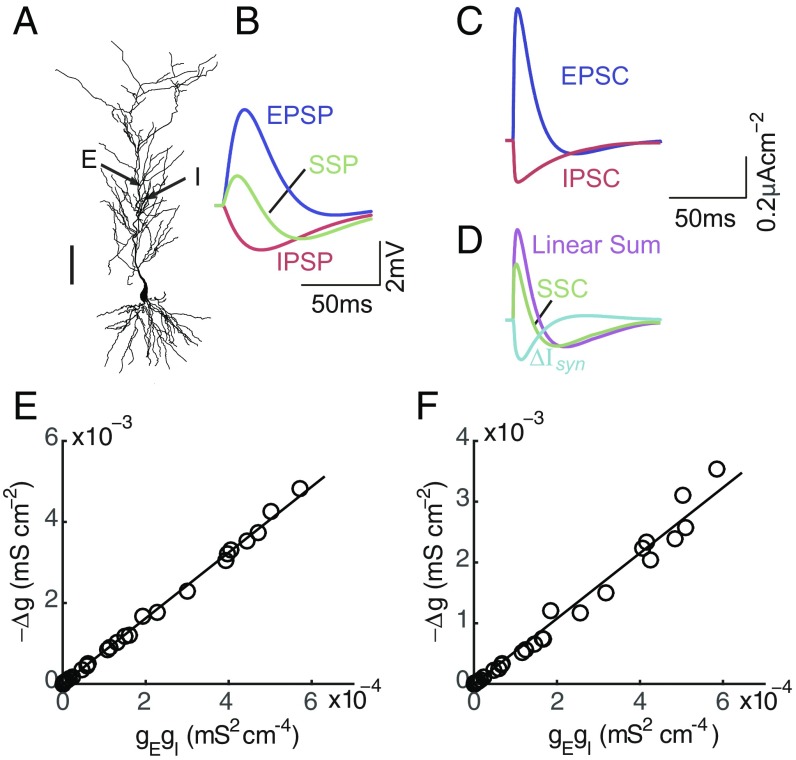
Fig. 2.
Realistic neuron simulation result of the bilinear conductance relation for a pair of E and I inputs. (A) The reconstructed hippocampal CA1 pyramidal neuron. Arrows indicate that the I and E inputs are given on the dendritic truck about 280 and 350 m away from the soma. (Scale bar: 100 m.) Model details can be found in refs. 21, 24, and 25. (B) A set of simulated individual EPSP, individual IPSP, and SSP induced by both E and I inputs. (C) Constructed EPSC and IPSC using the SSP and the E and I conductances estimated from the EPSP and IPSP in B. (D) The SSC estimated from the SSP in B, the linear sum of the constructed EPSC and IPSC in C, and the difference between them denoted as . (E) The bilinear relation between and the multiplication of and at the time when the E conductance reaches its peak value. The E and I inputs are given simultaneously. Line indicates linear fit (slope, k, = 0.998). (F) The same as E except that the I input is given 20 ms preceded to the E input. Line indicates linear fit (slope, k, = 0.979). In E and F, by varying the E and I input strengths, the amplitude of EPSP ranges from 0 to 6 mV, and the amplitude of IPSP ranges from 0 to −3 mV. Each circle corresponds to a set of EPSP, IPSP, and SSP.
Following the notation of the synaptic integration current to denote the difference between the SSC and the linear summation of the constructed EPSC and IPSC, we next verify whether the integration conductance obtained from still follows a bilinear relation with the E and I conductances as observed in experiment. Assuming that takes the form of Ohm’s law [i.e., ], by randomly varying the strengths of the E and I inputs with their input locations fixed, the integration conductance is indeed shown to be proportional to both and at each time point, confirming the bilinear relation . The bilinear relation at the peak time of the E conductance is illustrated in Fig. 2E (). Furthermore, the bilinear relation remains valid when the E and I inputs arrive nonconcurrently. As an illustration, a particular case of the bilinear relation is shown in Fig. 2F () when the I input is elicited 20 ms earlier than the E input. Consistent with our experimental observations, the integration coefficient in the bilinear relation is found to be independent of input strengths but is dependent of input arrival times (SI Appendix, Fig. S2).
Mechanism Underlying the Synaptic Current Integration.
To investigate the origin of the synaptic integration current , we perform the static 2-port analysis and show that it emerges from the interaction of synaptic inputs across the spatial dendrites (SI Appendix has details). In particular, from our analysis, the integration coefficient in the bilinear conductance relation can be expressed as
| [3] |
where , , and are the transfer resistances between the locations of the E and I inputs, between the locations of the E input and the soma, and at the soma, respectively. Therefore, only in the limiting case when the E and I inputs are given at the soma, we have . In this case, according to Eq. 3, the integration coefficient vanishes as does the synaptic integration current , hence the validity of the synaptic current description (Eq. 2). However, a neuron in general receives E and I inputs on the dendrites where and . In such a case, according to Eq. 3, deviates from zero; thus, the synaptic current description (Eq. 2) fails to characterize the synaptic current arriving at the soma of a spatial neuron with dendrites. Note that our 2-port analysis shows that the synaptic integration current is mostly negative (SI Appendix has details), indicating an additional I effect at the soma coming from the synaptic integration in addition to hyperpolarizing and shunting effects of I inputs. Consequently, the form of the synaptic current (Eq. 2) in the traditional point neuron framework underestimates the inhibition effect.
Integration of Identical-Type Synaptic Currents Revealed in Realistic Neuron Simulations.
Via realistic neuron simulations, we further discover that the synaptic integration current and the bilinear conductance relation exist for cases of both a pair of E inputs and a pair of I inputs. When 2 inputs of the same type are elicited simultaneously on the dendrites of the realistic neuron about 350 and m away from the soma, the SSC derived from the point neuron model is found to deviate from the linear sum of 2 individual synaptic currents when elicited individually. The difference between them is also denoted as and casted by the form of Ohm’s law: that is, , where () is the E or I reversal potential depending on the input type. By randomly varying the strengths of the 2 inputs without changing the input locations, the bilinear conductance relation can be observed as and , where and are the integration coefficients independent of input strengths and and () are the conductances measured when the 2 inputs are given separately. The bilinear relation at the time when one of the conductances reaches its peak value is illustrated in Fig. 3A for the case of 2 E inputs () and in Fig. 3B for the case of 2 I inputs (). Additional simulation results demonstrate that the integration coefficients vary at different time points (Fig. 4A) and are dependent of input arrival times. Note that, for the cases of both a pair of E inputs and a pair of I inputs, the expressions of the integration coefficients and in the bilinear conductance relation can be similarly obtained as in Eq. 3 using our 2-port analysis (SI Appendix has details), indicating the existence of the synaptic integration current in these cases.
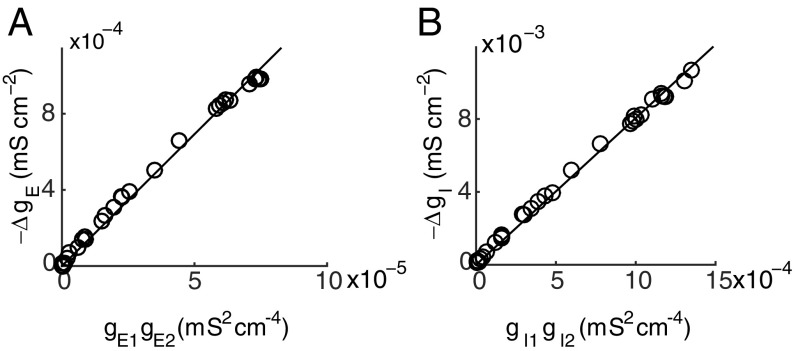
Fig. 3.
Realistic neuron simulation result of the bilinear conductance relation for a pair of synaptic inputs of the identical type. (A) The bilinear relation between and the multiplication of and . Data are collected by randomly changing the amplitude of EPSP from 0 to 4 mV. Line indicates linear fit (slope, k, ). (B) The bilinear relation between and the multiplication of and . Data are collected by randomly changing the amplitude of IPSP from 0 to −3 mV. Line indicates linear fit (slope, k, ). In A and B, the 2 E (I) inputs are given simultaneously on the dendritic trunk about 280 and 350 m away from the soma, and the data are measured at the time when one of the E (I) conductances reaches its peak value.
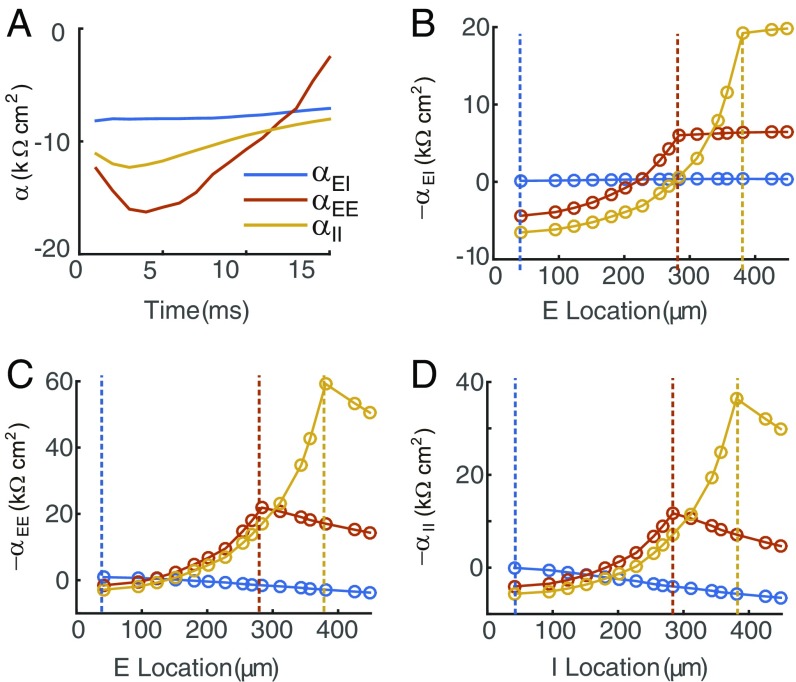
Fig. 4.
Spatiotemporal properties of the integration coefficients. (A) , , and as a function of time. (B) The spatial dependence of . For each color-coded curve, the I input is fixed at the location marked by the dashed line with identical color, and the E input moves along the dendritic trunk from the soma toward the distal dendrites. (C and D) The spatial profiles of and , respectively.
Spatiotemporal Dependence of the Integration Coefficients.
We next investigate the spatial dependence of the integration coefficients , , and in realistic neuron simulations. For a pair of E and I inputs, when the I input location is fixed, the dependence of the integration coefficient on the E input location shows a clear asymmetry for proximal vs. distal E input locations. To be specific, given an I input on the dendritic trunk, decreases rapidly as the distance between the E and I sites increases when the E input site is located between the soma and the I input site but remains constant when the E input site is located farther away from the soma than the I input site (Fig. 4B). In contrast, for a pair of E inputs, when 1 E input location is fixed, the dependence of the integration coefficient on the other E input location shows a clear symmetry for proximal vs. distal E input locations. Also, is largest when the 2 E input sites overlap with each other and decays when the distance between the 2 E inputs increases (Fig. 4C). The spatial dependence of is similar to that of (Fig. 4D). Accounting for the fact that a neuron receives the majority of synaptic inputs from its dendritic branches, we also investigate the spatial dependence of the integration coefficients on the whole dendrites. We find that the above spatial dependence of the integration coefficient still holds when 1 input site is fixed on the dendritic trunk and the other input site is scattered on the dendritic arbor (SI Appendix, Fig. S3). In addition, when 1 input site is fixed on a dendritic branch, the integration coefficient is significantly non-zero only when the other input site is within the same branch (SI Appendix, Fig. S3), consistent with the theory that each dendritic branch is an independent functional computational unit (26, 27). It has been further noticed that the integration coefficient for a pair of inputs within a branch is in general larger than that for 2 inputs at the dendritic trunk (SI Appendix, Fig. S3). All of these spatial properties of the integration coefficients observed in the simulations can be successfully explained from our 2-port analysis (SI Appendix has details).
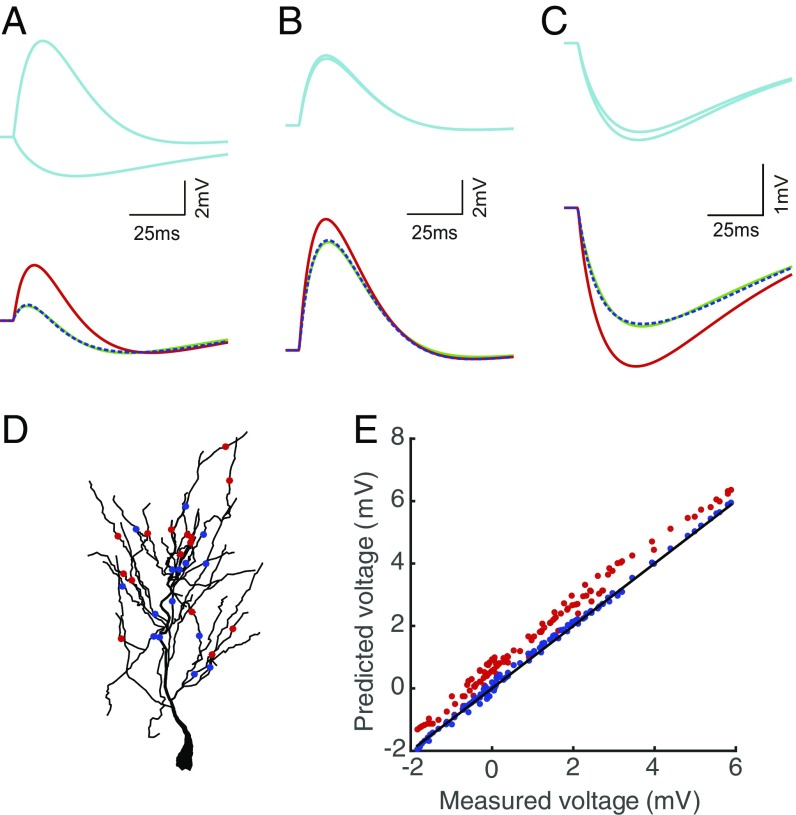
For the temporal dependence, although the integration coefficients are time dependent (Fig. 4A), the point neuron model can predict the SSP accurately by incorporating the synaptic integration currents with their coefficients approximated by time-independent constants as will be demonstrated in the simulation below. For a pair of E and I synaptic inputs, we first approximate the integration coefficient as a function of time by its value measured at the time when the E conductance reaches its peak value. The approximation can be justified by the fact that the integration conductance contributes dominantly to the synaptic integration current when is around its peak, and is insensitive to the value of when approaches zero away from its peak. We then build the point neuron model by including the synaptic integration current with the approximated constant integration coefficient. Given a pair of E and I inputs separately, we can measure the E and I conductance transients and use them in the point neuron model with the synaptic integration current incorporated to predict the SSP when the pair of E and I inputs is given simultaneously. We then compare the predicted SSP with the simulated SSP obtained from the realistic neuron when it receives the 2 inputs simultaneously. The simulation result shows that, given a pair of E and I inputs at a dendritic branch about 230 and 200 m away from the soma simultaneously, the predicted SSP from the point neuron model with the synaptic integration current incorporated almost overlaps with that recorded from the soma of the realistic neuron. In contrast, the SSP predicted by the point neuron model without the synaptic integration current deviates from the simulated SSP (Fig. 5A). Similar results are observed in the cases of a pair of E inputs and a pair of I inputs (Fig. 5 B and C). We note that the prediction error for the point neuron model without the synaptic integration current is significant (i.e., the relative error measured at the peak amplitude of the voltage trace is 248.9% for the E–I case, 20.8% for the E–E case, and 33.3% for the I–I case).
Fig. 5.
Synaptic integration current captures the somatic voltage dynamics shaped by spatiotemporal dendritic integration. (A–C) The SSP produced by the realistic neuron model (green) given a pair of (A) E–I, (B) E–E, and (C) I–I inputs (cyan), the SSP predicted by the point neuron model with the synaptic integration current using a constant integration coefficient (dashed blue), and the SSP predicted by the point neuron model without the synaptic integration current (red). The 2 inputs are given at dendritic branches about 230 and 200 m away from the soma. The integration coefficients in the 3 cases are , , and k, respectively. (D) Distribution of 15 E inputs (red dots) and 15 I inputs (blue dots) at the dendritic arbor in stratum radiatum of the realistic neuron model. (E) The SSPs predicted by the point neuron model with (blue) and without (red) the synaptic integration current are plotted against the measured SSP from the simulation of the realistic neuron model. The membrane potential from the realistic neuron model is obtained by setting the E and I inputs at locations shown in D, with the input arrival time at each location uniformly randomly distributed from 0 to 200 ms. For the ease of comparison, the slope of the black line is unity.
Generalization of Synaptic Integration Current for Multiple Synaptic Inputs.
When a neuron receives multiple E and I inputs, the synaptic current can be naturally generalized as
| [4] |
where the synaptic integration current is described as
| [5] |
The synaptic integration current describes the interaction of each paired input, and the sets of integration coefficients , , and encode the spatiotemporal information of synaptic inputs on the dendrites. In addition to the synaptic current description (Eq. 4), by incorporating the synaptic integration current (Eq. 5), the model accurately characterizes the synaptic currents arriving at the soma. As demonstrated from our numerical simulations, when the realistic neuron model receives 15 E synaptic inputs and 15 I synaptic inputs from its dendrites with uniformly distributed arrival times (Fig. 5D), its somatic voltage nearly overlaps with the SSP predicted by the point neuron model with the synaptic integration current while deviating from the SSP predicted by the point neuron model without the synaptic integration current (Fig. 5E).
Through electrophysiological experiments, realistic neuron simulations, and theoretical analyses, we demonstrate the existence of the synaptic integration current and the bilinear conductance relation with the integration coefficient encoding the spatiotemporal information of synaptic inputs on the dendrites of a spatial neuron. Under the point neuron framework, we show that the point neuron model by incorporating the synaptic integration current can accurately predict the somatic membrane potential of a spatial neuron with dendrites in response to synaptic inputs. Our results demonstrate that the spatiotemporal interaction among multiple synaptic inputs on the high-dimensional, nonlinear, active dendrites of a neuron can be decomposed into pairwise interactions for all pairs of synaptic inputs. In addition, the interaction between each pair of synaptic inputs can be reliably parameterized by a single integration coefficient, suggesting the inherent low-dimensional structure of the dendritic integration process.
Dendritic Phenomena Captured by the Synaptic Integration Current.
We next give 2 examples to illustrate that the derived point neuron model with the synaptic integration current incorporated is capable of capturing dendritic effects.
Countering dendritic filtering effect.
Our derived point neuron model predicts a phenomenon of dendritic filtering effect. Early experiments have shown that a local E synaptic input on the dendrite will be filtered by the dendritic cable property, resulting in a broader EPSP at the soma than that measured on the dendrite. This is known as the dendritic filtering effect. Because of this effect, the rising time of the somatic EPSP becomes slower as the distance between the E input location and the soma increases, indicating that the neuron may respond slower to inputs received at distal dendrites than at proximal dendrites (28). However, the existence for the synaptic integration current predicts that the dendritic filtering effect can be alleviated or even reversed in the presence of an I input. Given both E and I inputs, the effective E conductance becomes . Despite the fact that the E conductance (derived from the EPSC at the soma when the E input is given alone) rises slower for the input received at the distal dendrites than at the proximal dendrites, the effective E conductance can be shown to rise even faster for the distal E input with a large negative (Fig. 6 A, Left). Therefore, the SSP induced by the distal E input could rise faster than that induced by the proximal E input, countering the dendritic filtering effect (Fig. 6 A, Left).
Fig. 6.
Dendritic computations in a point neuron model with the synaptic integration current. (A) The countering dendritic filtering effect. In the presence of an I input, (A, Upper Left) the E conductance exhibits a faster rising time for a distal E input (red) than a proximal E input (blue). (A, Lower Left) The SSPs induced by both E and I inputs from the point neuron model with the synaptic integration current, which also exhibits a faster rising time for a distal E input (red) than a proximal E input (blue). (A, Right) The location dependence of the rising time of the individual EPSP and the SSP obtained in realistic neuron simulations. If an I input is elicited, its location is on the trunk about 250 m away from the soma. All voltages are normalized to have an identical amplitude. (B, Left) Schematic plot of the dendritic mechanism for direction selectivity. The red arrow indicates the preferred direction along which the activation of synapses will promote the activity of the neuron, while the blue arrow indicates the nonpreferred direction that has the opposite effect. (B, Right) The realization of direction selectivity in a point neuron model with the synaptic integration current for the preferred direction (red) and the nonpreferred direction (blue). (C, Left) Schematic plot of the dendritic mechanism for coincidence detection. Detection of coincident inputs is facilitated when the inputs are received on 2 separate branches. (C, Right) The realization of coincidence detection in a point neuron model with the synaptic integration current for the 2 inputs received on different branches (red) and on the same branch (blue). In B and C, the dashed lines indicate the firing threshold.
The predicted effect of countering dendritic filtering has been verified in realistic neuron simulations in which an I input is fixed in the middle of the dendritic trunk and an E input moves from the soma toward the distal dendrites. Simulation results demonstrate that, when only an E input is given on the dendrites, the time when the somatic EPSP reaches its peak value increases as the distance between the E input and the soma increases; however, when both E and I inputs are given on the dendrites, the time when the SSP reaches its peak value decreases as the distance between the E input and the soma increases (Fig. 6 A, Right). In addition to the phenomenon of countering dendritic filtering per se, the successful prediction made from the synaptic integration current suggests that one can investigate complex dendritic computations through the analysis of the simple form of the derived synaptic integration current as discussed above.
Bilinear dendritic integration rule.
Our point neuron model with the synaptic integration current incorporated is capable of capturing a bilinear rule of dendritic integration discovered in recent experiments (21, 24). In the experiments (21, 24), given a pair of glutamatergic E input and GABAergic I input simultaneously to a hippocampal CA1 pyramidal neuron, the SSP measured at the soma denoted by can be well characterized by a bilinear rule as , where and are the EPSP and IPSP measured at the soma when the E or I input is given alone, respectively, and is the shunting coefficient, which depends on the dendritic locations and arrival times of the E and I inputs but not the strengths of the inputs. In particular, the spatial dependence of measured at the time when the EPSP reaches its peak value exhibits the feature of spatial asymmetry: when the location of the I input is fixed on the dendritic trunk and the E input is located between the soma and the I input site, increases as the distance between the E input and the soma increases; when the E input is located farther away from the soma than the I input site, remains constant with further increase in the distance between the E input site and the soma. The bilinear rule of dendritic integration has also been observed for the integration of a pair of E inputs, a pair of I inputs, and a mixture of multiple E and I inputs in both experiments and realistic neuron simulations (24).
We point out that the point neuron model including the synaptic integration current can reliably capture the bilinear dendritic integration rule and its generalizations, and the shunting coefficient can be determined by the integration coefficient () (23). Furthermore, by using the 2-port analysis, we show that there is a linear mapping between the shunting coefficient and the integration coefficient (SI Appendix has details). From this mapping, one can elucidate the underlying mechanism of the bilinear dendritic integration rule and the spatially asymmetric feature of the shunting coefficient observed in the above experiment.
Dendritic Computations Performed by the Synaptic Integration Current.
Here, we show that the point neuron model with the synaptic integration current incorporated possesses the computational power of a spatial neuron with dendrites.
Direction selectivity.
A point neuron with the synaptic integration current is capable of performing the computation of direction selectivity. As predicted by Rall’s cable theory (29), the activation of a train of E inputs can promote the firing of a neuron when the inputs are received sequentially from the distal dendrite toward the soma but demote the firing when the E inputs are received in the reverse direction (Fig. 6B). In this way, the neuron has a preferred direction of input sequence. The sensitivity to spatiotemporal sequences of synaptic activation in cortical pyramidal neuron dendrites was observed in later experiments (2). In our derived synaptic integration current, the information of the input direction can be encoded in an ordered sequence of integration coefficients. In particular, the early activation of a pair of distal E inputs corresponds to the synaptic integration current with a large negative , and the late activation of a pair of proximal E inputs corresponds to the synaptic integration current with a small negative (SI Appendix has details). Therefore, given a temporal sequence of identical E inputs to the point neuron, its firing will be promoted by sequentially activating the set of with values that are in an increasing order but demoted by activating the set of in the reversed order (Fig. 6B).
Coincidence detection.
Similarly, a point neuron with the synaptic integration current can play the role of coincidence detector. In the early auditory pathway, neurons that receive bilateral inputs have bipolar dendrites, with each dendritic tree receiving input from only 1 ear (30). These neurons can detect input coincidence with submillisecond temporal resolution in their role of computing interaural arrival time difference, which is a cue for sound localization (Fig. 6C). In the point neuron model with the synaptic integration current, the detection of coincident inputs can be facilitated by a small negative in the synaptic integration current for a pair of E inputs representing the case of the inputs received on separate dendrites and will be depressed by a large negative in the corresponding synaptic integration current representing the case of the inputs received on the same dendrite (Fig. 6C and SI Appendix have details).
Logical operation.
The synaptic integration current enables a point neuron to perform logical operation. Previous studies have shown that one of the important functions of dendrites is to perform logical computation (3, 26). For instance, given a pair of E and I inputs, the I input is found to be maximally effective to silence the E input when the I input is received between the soma and the location of the E input, known as the “on-the-path effect” (3, 26). Therefore, given a pair of distal E synapse and proximal I synapse, to observe an output at the soma, it is required that the E synapse is activated, while the I synapse remains inactivated. Therefore, this pair of E and I inputs performs the logical operation of “E AND (NOT I).” In contrast, for an I input located farther away from the soma than the location of the E input—the out-of-the-path configuration—studies have shown that the I input exerts a weak influence on the E input. Therefore, this pair of E and I inputs no longer performs the logical operation of E AND (NOT I) but simply the gate of E. In addition, a pair of E inputs received at 2 separated branches in general will produce larger response at the soma of a neuron than a pair of E inputs received at the same branch. If the neuron requires at least 2 inputs to generate an output, the inputs are preferred to be at different branches. Therefore, 2 separate E inputs can play the role of an AND gate, while 2 nearby E inputs cannot. When a neuron receives multiple inputs distributed on the dendrites, the combination of the above-mentioned simple logical gates can give rise to complex logical operations. All of these logical operations can be easily achieved in the point neuron framework by measuring values of the integration coefficients in the synaptic integration current (Eq. 5), because the integration coefficients encode the locations of inputs that determine the type of logical computations.
Discussion
In this work, by using electrophysiological experiments, realistic neuronal simulations, and theoretical analyses, we have derived a form of synaptic current in the point neuron framework as a result of dendritic integration. In addition to the traditional form of the synaptic current (Eq. 4), our derived synaptic integration current described by Eq. 5 indicates that the interaction between each pair of synaptic inputs on the complex nonlinear active dendrites can be reliably captured by the bilinear interaction between their corresponding synaptic conductances. In addition, we have shown that the point neuron model with the synaptic integration current incorporated is able to capture many dendritic phenomena, including countering dendritic filtering, and a bilinear rule of dendritic integration discovered in a recent experiment, and the model possesses the computational ability of a spatial neuron with dendrites, including direction selectivity, coincidence detection, and logical operation.
When describing the synaptic integration current measured in our experiments and the simulations, we have chosen the reversal potential to be the E reversal potential. In fact, there is a degree of freedom for choosing the value of the reversal potential within the regime in which the ratio of the postsynaptic potential to the reversal potential is small, and the value of the integration coefficient depends on the choice of the reversal potential (SI Appendix has details). However, we stress that the bilinear interaction between the conductances remains valid when choosing a different reversal potential value (e.g., the I reversal potential), which has been justified in both our theoretical analysis (SI Appendix) and numerical simulations (SI Appendix, Fig. S1).
To reveal the mechanism underlying the existence of the synaptic integration current, for the simplicity of illustration, we have performed the steady-state analysis. By noticing that the static analysis fails to describe the temporal integration of synaptic inputs, we have also developed a strict analysis based on the dynamical cable equation when the model neuron receives time-dependent synaptic inputs. The dynamical analysis also gives rise to the identical form of synaptic integration current with time-dependent integration coefficients as a result of spatiotemporal dendritic integration.
According to the nonlinear integration between E and I conductances in the synaptic integration current, it behooves one to reexamine the ramifications of previous works involving the decomposition of E and I synaptic inputs. In many previous works, based on the form of the traditional synaptic current (Eq. 2), by holding the somatic membrane potential at various levels using the voltage clamp, the E and I synaptic conductances (9) and currents (10) are estimated from the linear I–V relation where the slope is the total conductance and the intercept is the reversal current . The measured conductances are often used to evaluate the state of a network (31). However, our work shows that the E and I conductances are not linearly separable but interact with each other nonlinearly. Therefore, the interpretation of the measured E and I components based on the traditional point neuron model is questionable.
We illustrate the issue of conductance measurement using realistic neuron simulations as shown in SI Appendix, Fig. S4. When a pair of E and I inputs is given at the dendritic trunk 350 and 280 m away from the soma of the realistic neuron model separately, we calculate the E and I conductances in the corresponding point neuron model as the reference conductances. Note that the reference conductance is different from the local conductance at the dendrite; instead, it reflects directly the functional impact of local synaptic inputs on the somatic membrane potential change and thereby, neuronal information processing at the soma. When the same pair of E and I inputs is given at the dendritic trunk simultaneously, by using the voltage clamp, the measured E and I conductances based on Eq. 2 significantly deviate from the reference conductances. In addition, in the case shown in SI Appendix, Fig. S4, the fact that inhibition is dominant to excitation can be misinterpreted as that E and I are approximately balanced. Through our analysis, the error is induced by neglecting the nonlinear integration between currents across the spatial dendrites when using the traditional point neuron framework.
It has been broadly believed that many dendritic phenomena, such as the integration of spatially distributed synaptic inputs, are beyond the scope of the existing point neuron models (32, 33). However, the dendritic integration process is known to have a strong impact on the action potential generation and thereby, neuronal information coding. Here, we have developed an effective point neuron model (i.e., a point neuron model with the synaptic integration current incorporated) that can capture many dendritic effects, and it has succinct structure for analysis and simulation. We have shown that the effective point neuron model can achieve the same order of accuracy for the somatic voltage dynamics as a detailed multicompartment model with substantially low computational costs (Fig. 5D).
Therefore, it is promising to develop fast algorithms for neuronal simulations to capture the dynamics of a neuron with realistic dendritic morphology. To be specific, the spatiotemporal profile of the integration coefficients encoding the information of synaptic inputs can be measured in advance and recorded in a library for future simulations. When simulating the point neuron model, the dendritic integration effect can be accurately captured by simulating the synaptic integration current with the integration coefficient read out from the library. It has been found in our simulation that the library of the integration coefficients is very sparse (SI Appendix, Fig. S5) (i.e., the majority of the coefficients are not large enough to induce a 5% change of SSP). This is consistent with previous works showing that the nonlinear interaction between a pair of inputs is mainly localized within a branch (26, 27). The sparsity of bilinear synaptic interactions benefits the simulation efficiency of our point neuron model. Consequently, the simulation speed is expected to be improved tremendously in comparison with simulating the realistic neuron model with full dendrites. The developed point neuron model in this work only describes the subthreshold regime without accounting for active channels associated with spike generation. However, this limitation could be potentially overcome by modeling the spike time as when the voltage reaches a firing threshold (i.e., the integrate-and-fire–type neuron). Another limitation of the developed point neuron model is that the integration current derived in our model so far only takes into account the second-order interaction of synaptic inputs; therefore, it may not be capable of capturing highly nonlinear dendritic phenomena, such as dendritic spikes and plateau potentials. Capturing these phenomena may involve the voltage dependence of the integration coefficients and higher-order interactions of synaptic inputs.
Furthermore, the form of the synaptic integration current reshapes the synaptic input modeling in both experiments and simulations. For instance, dynamic clamp has been extensively used in electrophysiological experiments, in which realistic E and I synaptic currents are generated at the soma of a neuron (34, 35) to mimic synaptic current dynamics. Based on our results, these synaptic currents are far from reality because of the neglect of the synaptic integration current. An appropriate way suggested by our results is to generate synaptic currents by incorporating the synaptic integration current (Eq. 5) in future studies.
Materials and Methods
Slice Electrophysiology.
The experimental procedure of whole-cell recording and microiontophresis on hippocampal CA1 pyramidal neurons in acute brain slices (350-m thick) of juvenile Sprague–Dawley rats (postnatal days 15 to 20) followed the methods described in our previous study (21). The animal experimental protocols were approved by the Animal Use and Care Committee of the State Key Laboratory of Cognitive Neuroscience & Learning at Beijing Normal University (IACUC-BNU-NKLCNL-2016-02).
Realistic Neuron Simulation.
We adapted the multicompartment neuron model used in our previous studies (21, 24, 25) for our realistic pyramidal neuron simulation. The morphology of the reconstructed pyramidal neuron, which includes 200 compartments, was obtained from the Duke–Southampton Archive of Neuronal Morphology (36). The passive cable properties and the densities of active conductances in the neuron model were based on published experimental data obtained from the hippocampal and cortical pyramidal neurons (27, 37–48). In particular, the multicompartment neuron model included the voltage-gated sodium channel, the delayed rectifier potassium channel, 2 variants of the A-type potassium channel, and the hyperpolarization activated channel. The E and I synaptic inputs were given through AMPA and receptors, respectively. The resting potential was set to mV, and the E and I reversal potentials were set to and mV. We used the NEURON software Version 7.4 (49) to simulate the model with a time step of 0.1 ms.
Supplementary Material
Acknowledgments
We thank Li Yao for providing the neuron image in Fig. 1A. This work was supported by NYU Abu Dhabi Research Institute Grant G1301 (to S.L., D.Z., and D.C.); Shanghai Sailing Program 19YF1421400 (S.L.); Beijing Municipal Science & Technology Commission Grant Z181100001518001 (to X.Z.); Shanghai Grants 14JC1403800 and 15JC1400104 (to D.Z. and D.C.); Shanghai Rising-Star Program 15QA1402600 (to D.Z.); and Natural Science Foundation of China Grants 11671259, 11722107, 91630208 (all to D.Z.), and 3157107 (to D.C.).
Footnotes
Reviewers: L.A., Columbia University; and D.L.R., University of California, Los Angeles.
The authors declare no conflict of interest.
Data deposition: The source code for our model has been deposited on GitHub at https://github.com/songting858/DIF_model.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1904463116/-/DCSupplemental.
References
- 1.London M., Häusser M., Dendritic computation. Annu. Rev. Neurosci. 28, 503–532 (2005). [DOI] [PubMed] [Google Scholar]
- 2.Branco T., Clark B. A., Häusser M., Dendritic discrimination of temporal input sequences in cortical neurons. Science 329, 1671–1675 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Koch C., Biophysics of Computation: Information Processing in Single Neurons (Oxford University Press, 2004). [Google Scholar]
- 4.Dayan P., Abbott L. F., Theoretical Neuroscience (MIT Press, Cambridge, MA, 2001), vol. 31. [Google Scholar]
- 5.Gerstner W., Kistler W. M., Spiking Neuron Models: Single Neurons, Populations, Plasticity (Cambridge University Press, 2002). [Google Scholar]
- 6.Priebe N. J. et al., Direction selectivity of excitation and inhibition in simple cells of the cat primary visual cortex. Neuron 45, 133–145 (2005). [DOI] [PubMed] [Google Scholar]
- 7.Wehr M., Zador A. M., Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature 426, 442–446 (2003). [DOI] [PubMed] [Google Scholar]
- 8.Cruikshank S. J., Lewis T. J., Connors B. W., Synaptic basis for intense thalamocortical activation of feedforward inhibitory cells in neocortex. Nat. Neurosci. 10, 462–468 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Anderson J. S., Carandini M., Ferster D., Orientation tuning of input conductance, excitation, and inhibition in cat primary visual cortex. J. Neurophysiol. 84, 909–926 (2000). [DOI] [PubMed] [Google Scholar]
- 10.Monier C., Fournier J., Frégnac Y., In vitro and in vivo measures of evoked excitatory and inhibitory conductance dynamics in sensory cortices. J. Neurosci. Methods 169, 323–365 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Chance F. S. et al., Gain modulation from background synaptic input. Neuron 35, 773–782 (2002). [DOI] [PubMed] [Google Scholar]
- 12.Piwkowska Z., et al. , Characterizing synaptic conductance fluctuations in cortical neurons and their influence on spike generation. J. Neurosci. Methods 169, 302–322 (2008). [DOI] [PubMed] [Google Scholar]
- 13.McLaughlin D., Shapley R., Shelley M., Wielaard D. J., A neuronal network model of macaque primary visual cortex (v1): Orientation selectivity and dynamics in the input layer 4c. Proc. Natl. Acad. Sci. U.S.A. 97, 8087–8092 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tao L., Shelley M., McLaughlin D., Shapley R., An egalitarian network model for the emergence of simple and complex cells in visual cortex. Proc. Natl. Acad. Sci. U.S.A. 101, 366–371 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Compte A., Brunel N., Goldman-Rakic P. S., Wang X.-J., Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb. Cortex 10, 910–923 (2000). [DOI] [PubMed] [Google Scholar]
- 16.Rudolph M., Pospischil M., Timofeev I., Destexhe A., Inhibition determines membrane potential dynamics and controls action potential generation in awake and sleeping cat cortex. J. Neurosci. 27, 5280–5290 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang X., Kendrick K. M., Zhou H., Zhan Y., Feng J., A computational study on altered theta-gamma coupling during learning and phase coding. PLoS One 7, e36472(2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cai D., Rangan A. V., McLaughlin D. W., Architectural and synaptic mechanisms underlying coherent spontaneous activity in v1. Proc. Natl. Acad. Sci. U.S.A. 102, 5868–5873 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhou D., Rangan A. V., McLaughlin D. W., Cai D., Spatiotemporal dynamics of neuronal population response in the primary visual cortex. Proc. Natl. Acad. Sci. U.S.A. 110, 9517–9522 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dai W. P., Zhou D., McLaughlin D. W., Cai D., Mechanisms underlying contrast-dependent orientation selectivity in mouse v1. Proc. Natl. Acad. Sci. U.S.A. 115, 11619–11624 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hao J., Wang X.-d., Dan Y., Poo M.-m., Zhang X.-h., An arithmetic rule for spatial summation of excitatory and inhibitory inputs in pyramidal neurons. Proc. Natl. Acad. Sci. U.S.A. 106, 21906–21911 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Badel L., et al. , Extracting non-linear integrate-and-fire models from experimental data using dynamic i–v curves. Biol. Cybernetics 99, 361–370 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhou D., Li S., Zhang X.-h., Cai D., Phenomenological incorporation of nonlinear dendritic integration using integrate-and-fire neuronal frameworks. PLoS One 8, e53508 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li S., Liu N., Zhang X.-h., Zhou D., Cai D., Bilinearity in spatiotemporal integration of synaptic inputs. PLoS Comput. Biol. 10, e1004014 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li S., Zhou D., Cai D., Analysis of the dendritic integration of excitatory and inhibitory inputs using cable models. Commun. Math. Sci. 13, 565–575 (2015). [Google Scholar]
- 26.Koch C., Poggio T., Torre V., Nonlinear interactions in a dendritic tree: Localization, timing, and role in information processing. Proc. Natl. Acad. Sci. U.S.A. 80, 2799–2802 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Poirazi P., Brannon T., Mel B. W., Pyramidal neuron as two-layer neural network. Neuron 37, 989–999 (2003). [DOI] [PubMed] [Google Scholar]
- 28.Stuart G., Spruston N., Häusser M., Dendrites (Oxford University Press, 2016). [Google Scholar]
- 29.Rall W., The Theoretical Foundation of Dendritic Function: Selected Papers of Wilfrid Rall with Commentaries (MIT Press, 1995). [Google Scholar]
- 30.Agmon-Snir H., Carr C. E., Rinzel J., The role of dendrites in auditory coincidence detection. Nature 393, 268–272 (1998). [DOI] [PubMed] [Google Scholar]
- 31.Shu Y., Hasenstaub A., McCormick D. A., Turning on and off recurrent balanced cortical activity. Nature 423, 288–293 (2003). [DOI] [PubMed] [Google Scholar]
- 32.Gerstner W., Naud R., How good are neuron models? Science 326, 379–380 (2009). [DOI] [PubMed] [Google Scholar]
- 33.Herz A. V. M., Gollisch T., Machens C. K., Jaeger D., Modeling single-neuron dynamics and computations: A balance of detail and abstraction. Science 314, 80–85 (2006). [DOI] [PubMed] [Google Scholar]
- 34.Destexhe A., Bal T., Dynamic-Clamp: From Principles to Applications (Springer, 2009). [Google Scholar]
- 35.Prinz A. A. et al., The dynamic clamp comes of age. Trends Neurosci. 27, 218–224 (2004). [DOI] [PubMed] [Google Scholar]
- 36.Cannon R. C., Turner D. A., Pyapali G. K., Wheal H. V., An on-line archive of reconstructed hippocampal neurons. J. Neurosci. Methods 84, 49–54 (1998). [DOI] [PubMed] [Google Scholar]
- 37.Destexhe A., Mainen Z. F., Sejnowski T. J., An efficient method for computing synaptic conductances based on a kinetic model of receptor binding. Neural Comput. 6, 14–18 (1994). [Google Scholar]
- 38.Destexhe A., Mainen Z. F., Sejnowski T. J., Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J. Comput. Neurosci. 1, 195–230 (1994). [DOI] [PubMed] [Google Scholar]
- 39.Poirazi P., Brannon T., Mel B. W., Arithmetic of subthreshold synaptic summation in a model ca1 pyramidal cell. Neuron 37, 977–987 (2003). [DOI] [PubMed] [Google Scholar]
- 40.Stuart G., Spruston N., Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J. Neurosci. 18, 3501–3510 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Magee J. C., Johnston D., Characterization of single voltage-gated na+ and ca2+ channels in apical dendrites of rat ca1 pyramidal neurons. J. Physiol. 487, 67–90 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hoffman D. A., Magee J. C., Colbert C. M., Johnston D., K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature 387, 869–875 (1997). [DOI] [PubMed] [Google Scholar]
- 43.Migliore M., Hoffman D. A., Magee J. C., Johnston D., Role of an a-type k+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J. Comput. Neurosci. 7, 5–15 (1999). [DOI] [PubMed] [Google Scholar]
- 44.Magee J. C., Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal ca1 pyramidal neurons. J. Neurosci. 18, 7613–7624 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Magee J. C., Cook E. P., Somatic epsp amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat. Neurosci. 3, 895–903 (2000). [DOI] [PubMed] [Google Scholar]
- 46.Andrásfalvy B. K., Magee J. C., Distance-dependent increase in ampa receptor number in the dendrites of adult hippocampal ca1 pyramidal neurons. J. Neurosci. 21, 9151–9159 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Smith M. A., Ellis-Davies G. C. R., Magee J. C., Mechanism of the distance-dependent scaling of schaffer collateral synapses in rat ca1 pyramidal neurons. J. Physiol. 548, 245–258 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nicholson D. A., et al. , Distance-dependent differences in synapse number and ampa receptor expression in hippocampal ca1 pyramidal neurons. Neuron 50, 431–442 (2006). [DOI] [PubMed] [Google Scholar]
- 49.Carnevale N. T., Hines M. L., The NEURON Book (Cambridge University Press, 2006). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.