Figure 4. .

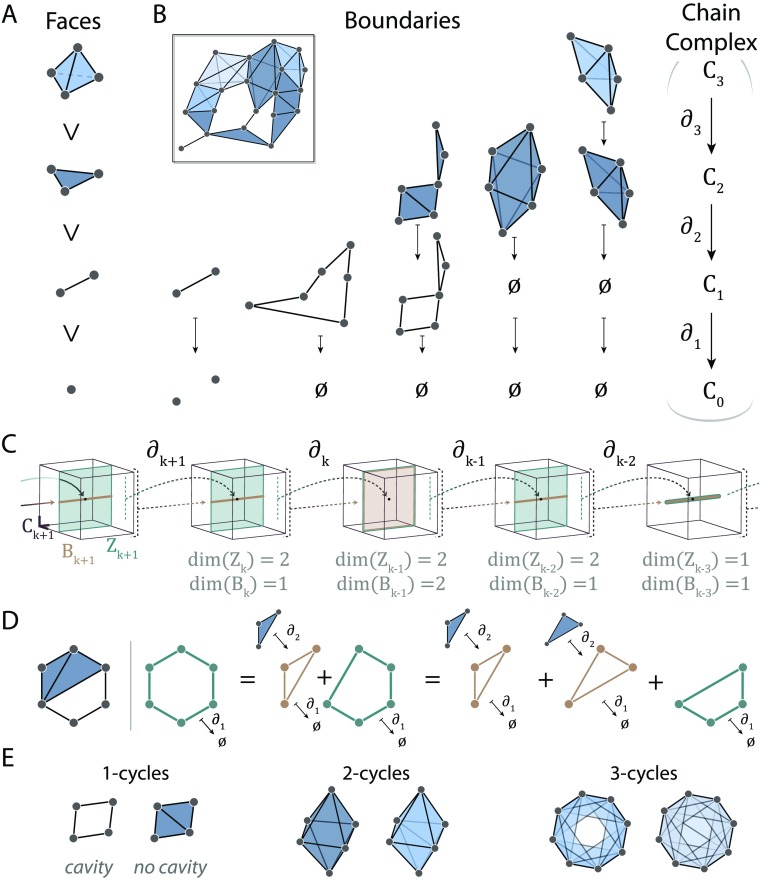
Chain complexes and homology. (A) A 3-simplex (top) has 2-simplices, 1-simplices, and 0-simplices as faces. (B) Boundary maps take k-chains to their boundaries. Examples shown for dimensions 1 through 3. These boundary maps connect the chain groups forming the chain complex (right). (C) Depiction of a chain complex with 3-dimensional chain groups (maroon boxes). Boundaries (gold) and cycles (green) are defined using the boundary operator and may span the same space, or the boundary space may be a strict subspace of the cycle space. (D) Given the simplicial complex shown at the (left), the three green cycles are equivalent because they differ by boundary cycles (gold). (E) Examples of k-cycles for k = 1 (left), k = 2 (middle), and k = 3 (right). For each k we show a non-trivial (cavity-enclosing) cycle on the left and a trivial cycle on the right.