The Effect of Angioscotomas on Map Structure in Primary Visual Cortex

Abstract

When blood vessels occlude the photoreceptor layer in the retina, they cast shadows onto the photoreceptors, creating angioscotomas (regions of the visual field to which that eye is blind). Remarkably, Adams and Horton (2002) have recently shown that it is sometimes possible to observe representations of these angioscotomas anatomically in the primary visual cortices of squirrel monkeys. However, there is substantial variability in the degree and form of these representations. The source of this variability is difficult to determine experimentally, because experimental studies are unavoidably limited by small sample size. In addition, experimental studies cannot compare the map structure that would develop with and without an angioscotoma. Here, we investigate these phenomena computationally using feature-mapping models of visual cortical development, which are not subject to the same limitations. These models suggest that the primary source of variability in angioscotoma representation is the precise timing of the onset of visual experience relative to the time course of ocular dominance column segregation. Furthermore, the models predict that angioscotomas could compete for control of local column layout with other influences such as cortical shape but that they have a small effect on the structure of orientation preference maps.

Introduction

In the primary visual cortices of many species of monkeys, neurons respond preferentially to stimuli in either the right or left eye. Together, these neurons form a pattern of interleaved monocular columns known as an ocular dominance (OD) map (LeVay et al., 1975) (for review, see Horton and Adams, 2005). The structure of these columns can be affected by artificial manipulations of the input activity in the two eyes (for instance, monocular deprivation) [for review, see Hubel and Wiesel (1977) and Katz and Shatz (1996)]. Specifically, a lack of input from one eye causes regions of cortex that would normally represent that eye to be invaded by afferents from the open eye. A natural and ubiquitous form of monocular deprivation exists in the form of angioscotomas. These are blind regions in the visual field of each eye resulting from the fact that the blood vessels in the retina, which radiate from the optic disc, are located in front of the photoreceptors and consequently deprive some photoreceptors of input from the visual field.

Remarkably, it was recently shown that angioscotomas are represented in the primary visual cortical maps of some squirrel monkeys (Adams and Horton, 2002, 2003b). They were revealed in OD maps created by cytochrome oxidase staining after monocular enucleation and appear as patterns of fine processes radiating from the optic disc representation (Fig. 1A,B). The discovery of cortical representations of angioscotomas provides additional clear evidence that imbalance of visual activity can influence the structure of the visual cortex.

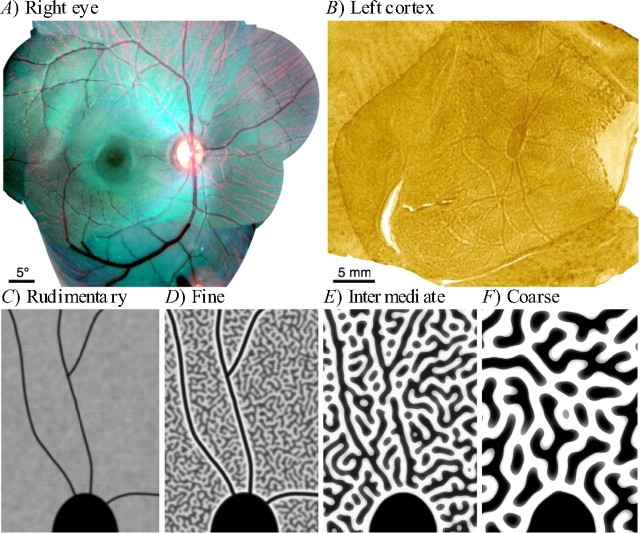
Figure 1.

Angioscotoma representations in squirrel monkey cortex as revealed by Adams and Horton (2002, 2003b). A, Fundus photograph of the optic disc and vascular tree of the right retina of a squirrel monkey. B, An OD map with an angioscotoma representation in the left striate cortex of the same squirrel monkey, created by cytochrome oxidase staining after right-eye enucleation. Dark regions correspond to neurons that receive input from the left eye only, and light regions are neurons that receive input from the right eye only. The large patch of cytochrome oxidase activity in the center is the right eye's optic disc representation. The large light area on the right is the monocular crescent. The thin processes extending from the optic disc are the right-eye angioscotoma representations. C–F, Schematic characterization of the relationship between OD column periodicity and angioscotoma visibility in the cortex (pictures are diagrams rather than actual data) (Adams and Horton, 2003b). Black represents afferents from one retina, and white represents afferents from the other. Shown in each panel is the superior half of the blind spot representation. The four panels show examples of different column periodicities in a continuous spectrum. C, Individuals with rudimentary columns have clear, thin angioscotoma representations. D, Individuals with fine columns have the clearest representations, because representations are highlighted by an outline of columns serving the other eye (frosting). E, In individuals with intermediate columns, angioscotoma representations are disrupted by the columnar pattern. F, In individuals with coarse, well segregated OD columns, there are no angioscotoma representations. A, B, Reprinted with permission from Adams and Horton (2002). C–F, Reprinted with permission from Adams and Horton (2003b).

Adams and Horton (2003b) found that the degree of angioscotoma representation varied greatly between individuals and was correlated with OD column periodicity (Fig. 1C–F). In animals with fine columns, the angioscotoma representations were outlined by a strip of opposing contrast, an effect that Adams and Horton (2003b) termed “frosting” (Fig. 1D). However, a more complete analysis of these intriguing phenomena has been precluded by experimental limitations such as the impossibility of knowing what the overall pattern would have been without an angioscotoma and the high degree of natural variability and relatively small sample size inherent in monkey studies. Furthermore, possible effects of angioscotomas on orientation (OR) maps cannot be easily investigated by experimental methods. In addition, it seems hard to explain the frosting effect, because it is not obvious why either eye should enjoy a competitive advantage in the cortex adjacent to an angioscotoma representation (Horton and Adams, 2005).

The experimental limitations discussed above do not apply to computational studies of map development. Here, we use the elastic net (Durbin and Willshaw, 1987) and Kohonen (Kohonen, 1982) models to simulate the presence of angioscotomas during OD and OR map development across a broad range of parameters. In reproducing the basic results observed by Adams and Horton (2002, 2003b), our simulations show that the degree of angioscotoma representation depends on the segregation of OD columns at the onset of visual experience. Our results also reveal an explanation for the frosting effect. Finally, we show that in the elastic net model, the degree of angioscotoma representation is affected by cortical shape and that angioscotomas can slightly affect the structure of OR maps.

Materials and Methods

Feature-mapping models.

Many different computational models for visual map development have been proposed [for review, see Erwin et al. (1995) and Swindale (1996)]. In most of these, a set of visual inputs is mapped onto a two-dimensional array of cells representing the primary visual cortex. For reasons discussed below, in this work we used the elastic net and Kohonen algorithms, both of which are based on Hebbian-type learning rules.

In the Kohonen algorithm (Kohonen, 1982), an input activity pattern v_i is presented. The cortical cell j* whose receptive field w_j best matches the input is then chosen, and the receptive field is adapted toward the input pattern. Here, we define the best-matching cortical cell j* as that with the smallest Euclidean distance between its weights vector and the input vector:

To model the effects of local lateral connections in the cortex, the receptive fields of nearby cells are also adapted toward the input pattern in proportion to a Gaussian function of their cortical distance from the winning unit:

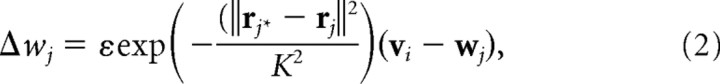where r_j specifies the cortical coordinates of cortical cell j, and ε is a small learning rate. Over the course of a simulation, K is gradually reduced, modeling a gradual refinement of cortical cell receptive fields during development.

The elastic net algorithm (Durbin and Willshaw, 1987) is similar but has a slightly different learning rule. The activity of each cortical cell in response to input v_i is first given by the following:

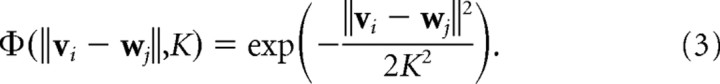These initial activities are then normalized to ensure that each input pattern produces the same overall amount of activity in the cortex:

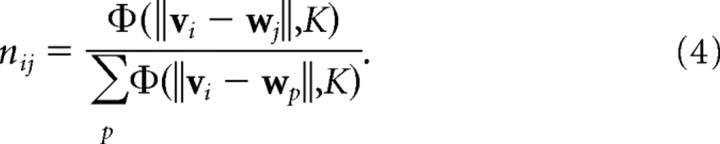The receptive fields of cortical cells are then adapted toward the input pattern in proportion to the degree n_ij to which they responded:

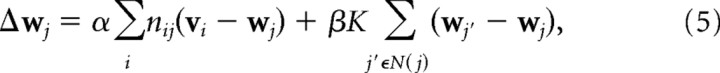where N(j) refers to the set of cells in the cortical sheet that are neighboring to j. Thus, the second term in Equation 5 implements the effects of local lateral connections by also adapting the receptive fields of neighboring cortical cells toward each other. The relative strengths of these two terms are controlled by the ratio α/β. K is again reduced over the course of a simulation.

Both the Kohonen and elastic net algorithms are Hebbian in that receptive fields adapt toward input patterns according to how strongly each cell was activated by the input pattern. There is substantial evidence that Hebbian-type learning is important in the development of visual receptive fields (Frégnac et al., 1988; Kirkwood and Bear, 1994; Frenkel et al., 2006).

As in previous work (Goodhill and Willshaw, 1990; Durbin and Mitchison, 1990; Obermayer et al., 1992), we use a simplifying abstraction of these models that speeds up computation while still producing results in good agreement with biological data. Specifically, we assume that each combination of input features, such as an oriented edge at a particular position in space observed through a specific eye, is treated simply as a point in a low-dimensional space, rather than being explicitly represented by pixel values in a high-dimensional image. Although this abstraction makes it harder to directly interpret some of the parameters, such “feature-mapping” or “low-dimensional” models also offer advantages over “high-dimensional” models (Willshaw and von der Malsburg, 1976; Miller et al., 1989; Obermayer et al., 1990; Goodhill, 1993). From a computational point of view, feature-mapping models are relatively robust and efficient. From a biological point of view, they have been shown to produce a close match to much of the experimental data regarding the structure of OD, OR, direction, and spatial frequency maps in primary visual cortex (V1), including their geometrical relationships (Erwin et al., 1995; Swindale, 1996; Swindale and Bauer, 1998; Carreira-Perpiñán et al., 2005). The elastic net in particular has also been shown to reproduce the experimentally observed effects on map structure of single-orientation rearing (Carreira-Perpiñán et al., 2005) and monocular deprivation (Goodhill and Willshaw, 1994; Carreira-Perpiñán et al., 2005), including the colocalization of pinwheels with the center of deprived-eye patches that has been observed experimentally (Crair et al., 1997).

The elastic net Equations 3–5 can be integrated to produce an objective function

that is minimized during the learning process (Durbin and Willshaw, 1987). Here,

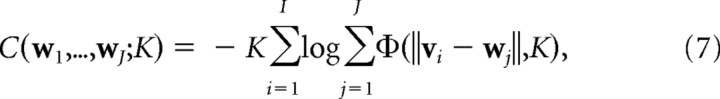and in the one-dimensional case,

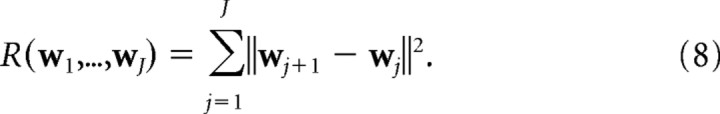The C or “coverage” (Swindale, 1991) term attempts to match cortical receptive fields to the input features, whereas the R (“continuity”) term attempts to keep neighboring cortical points close together in feature space. The elastic net algorithm can then be seen as attempting to optimize the trade-off between coverage, C, of the feature space and continuity, R, in cortical space, where the parameters α and β weight the relative importance of C and R. K can now be interpreted as an “annealing” parameter that scales the distance over which the coverage term acts. The general theoretical framework of models based on coverage versus continuity constraints is discussed in Swindale (1991, 1996, 2004), and a more detailed discussion of the elastic net can be found in Carreira-Perpiñán and Goodhill (2002). It is more computationally efficient to perform the optimization using more sophisticated methods than the simple gradient descent given by Equation 5. As described previously by Carreira-Perpiñán and Goodhill (2004) and Carreira-Perpiñán et al. (2005), here we used Cholesky factorization.

The feature space and training regime.

When applying these feature-mapping algorithms, there are different ways in which the feature space can be populated and the net trained. For the elastic net simulations, we used a regular array of feature points presented simultaneously, because (1) only a relatively small number of training points are then required to produce smooth maps, (2) batch learning can be applied to increase the speed of optimization, and (3) using this approach has previously been shown to produce map structure closely resembling that seen biologically (Carreira-Perpiñán et al., 2005). For the Kohonen simulations, one stimulus point was chosen at each iteration from a regular array of feature points. One-dimensional Kohonen simulations in which the stimuli were drawn from a uniform, random distribution gave similar results to the regular array simulations (data not shown).

We anneal the scaling parameter K for both the elastic net and the Kohonen algorithms over the course of the simulation. Such annealing was originally motivated by the application of these algorithms to combinatorial optimization problems such as the traveling salesman problem (Durbin and Willshaw, 1987; Fort, 1988), in which the annealing proved to be an effective way of producing highly optimized solutions (Rose, 1998). When these algorithms were subsequently applied to understand biological maps (Goodhill and Willshaw, 1990; Obermayer et al., 1992), the annealing was interpreted as a gradual, intrinsically determined reduction in synaptic plasticity during development, culminating in a “freezing” of the state of the map, modeling the end of the critical period for map plasticity (cf. Hensch, 2004). It is known (Goodhill and Willshaw, 1990) that the deterministic annealing strategy (Rose, 1998) used here does not generally produce global minima of objective functions such as Equation 6; rather, they represent an attempt to optimize within the confines of external (to the algorithm) constraints on map plasticity. When the global minimum can be directly calculated, it generally does not match a biological map. The optimization trajectory followed by the algorithm appears to be constrained so that it finds only local minima of the objective function, but these local optima are those that match biological maps. An example of such a constraint is that generally the spatial map appears before the OD map, which prevents the mapping of both ends of the cortex to the same end of an eye, which would be required for the global optimum (Goodhill and Willshaw, 1990). As previously described, this approach generates results matching much of the experimental data regarding the structure of maps in primary visual cortex.

The parameters used in this study were generally similar to those used by Carreira-Perpiñán et al. (2005). In the one-dimensional cortex simulations (see Figs. 2, 3), a one-dimensional cortical rope connecting 200 cortical points was mapped to one dimension of visual field and an orthogonal dimension of OD. The feature points in the visual field were a line of N_x = 50 points evenly spaced in the interval [0,1]. The OD dimension had two values at −l and l, giving a total of 50 × 2 = 100 feature points. Two parameters were varied between simulations: l, which can be related inversely to the correlation between eyes (Yuille et al., 1996), and the time of angioscotoma introduction, K_b (b signifying “birth”).

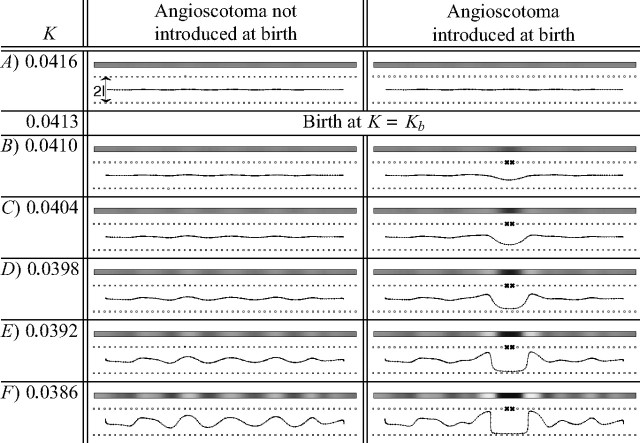
Figure 2.

Development of the same OD map without and with an angioscotoma demonstrates how the angioscotoma alters normal map formation. In the right column, an angioscotoma (marked with crosses; α = 0) was introduced at K_b = 0.0413. The left column shows the development of the same OD map when the angioscotoma is not introduced. The introduction of an angioscotoma at K_b causes the cortex to develop an angioscotoma representation with frosting. The width of the angioscotoma representation in F is approximately the same as the width of the just-segregating OD columns. For both simulations, the elastic net algorithm was used with l = 0.05 and all other parameters the same in each case. The grayscale pictures show how OD changes as the cortex is traversed: black represents afferents from the bottom retina, and white represents afferents from the top (where top and bottom correspond arbitrarily to the right and left eye biologically). The line drawings show the one-dimensional elastic rope of cortical points and the two rows of retinal points spanning a one-dimensional visual field. The horizontal position of cortical points indicates the position they represent in one-dimensional visual space, and the vertical position indicates ocularity (as in Goodhill and Willshaw, 1990). The crosses in the right column mark the position of the blood vessel after birth.

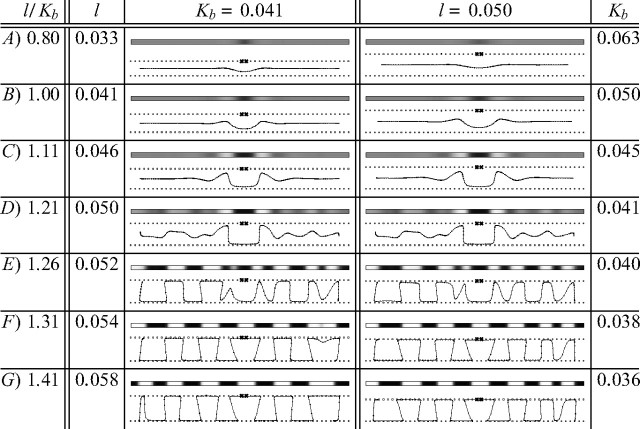
Figure 3.

Different degrees of angioscotoma representation similar to those observed experimentally are produced in one-dimensional cortices using the elastic net algorithm of visual cortical development by altering the ratio l/K_b. For the simulations in the left column, birth time K_b was constant, while l varied. In the right column, l was constant, while K_b was varied. A larger l value corresponds to faster OD column development, whereas a smaller K_b value corresponds to later birth (and hence angioscotoma introduction) when column formation is more advanced. All other parameters were the same in each case. For all simulations, annealing continued at the same rate for 10 iterations after angioscotoma introduction. The grayscale pictures show how OD changes as the cortex is traversed: black represents afferents from the bottom retina, and white represents afferents from the top (where top and bottom correspond arbitrarily to the right and left eye biologically). Note the frosting clearly apparent in B–D. The line drawings show the one-dimensional elastic rope of cortical points and the two rows of retinal points spanning a one-dimensional visual field. The horizontal position of cortical points indicates the position they represent in one-dimensional visual space, and the vertical position indicates ocularity (as in Goodhill and Willshaw, 1990). The crosses mark the position of the blood vessel after birth.

The next simulations (see Figs. 4, 6) extended the visual field to two dimensions so that feature points in the visual field formed a grid of (N_x = 50) × (N_y = 50) points in the rectangle [0,1] × [0,1]. The 50 × 50 point representation of the visual field was finer than the 20 × 20 point representation used by Carreira-Perpiñán et al. (2005) to more smoothly represent a tree-like blood vessel structure. The OD dimension remained the same as for the one-dimensional cortex case with feature points at −l and l. For these simulations, a two-dimensional cortical net of 64 × 64 = 4096 points was mapped to the training set of 50 × 50 × 2 = 5000 feature points. The rectangular cortex simulations (see Fig. 7) used larger elastic nets of 64 × 96 = 6144 and 64 × 128 = 8192 points.

Figure 4.

Different degrees of angioscotoma representation similar to those observed experimentally (Fig. 1) are produced in two-dimensional cortices using the elastic net algorithm. A–L, Different degrees of representation were generated by changing the ratio l/K_b, which controls how segregated the OD columns are at birth. A–L, Two-dimensional versions of the simulations in Figure 3. K, M–O, Representations of different-shaped angioscotomas in cortex with l = 0.05 and K_b = 0.038. These show that the degree of angioscotoma representation is independent of the specific shape of the angioscotoma. K, P–R, Angioscotoma representations in different cortices with l = 0.05 and K_b = 0.038 produced in the elastic net by starting the net from different random initial configurations. These show that the influence of the angioscotoma is largely independent of the particular pattern of columns that would have formed otherwise. All other parameters were the same in each case. For all simulations, annealing was continued at the same rate for 10 iterations after angioscotoma introduction. The red crosses indicate the cortical locations of the feature points that are deprived after birth. Black represents afferents from one retina, and white represents afferents from the other.

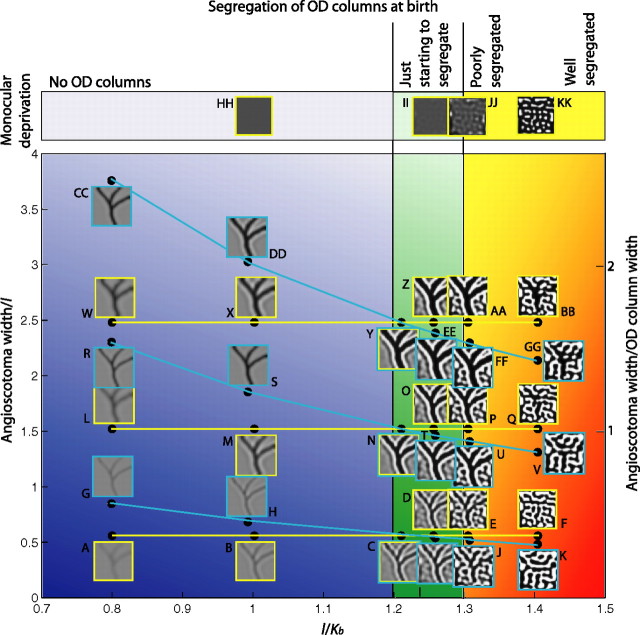
Figure 6.

A–GG, Increasing the width of the deprived region relative to the width of OD columns increases the visibility of the angioscotoma representation but does not reproduce the different degrees of angioscotoma representation observed experimentally (Adams and Horton, 2003b). To pass through the four regions of the phase diagram corresponding to the four different types of representation observed experimentally (blue, green, orange and red regions; compare with Fig. 1C–F), the segregation of the OD columns at birth must be varied by changing the width of the OD columns (changing l, cyan lines), the time of birth (changing K_b, yellow lines), or both. Changing angioscotoma width relative to OD column width alone, corresponding to moving purely vertically, does not reproduce the four types of representation observed experimentally. HH–KK, For comparison, complete monocular deprivation can produce a significant rearrangement in the cortex, even when an angioscotoma produces little or no rearrangement (compare F, KK).

Figure 7.

Cortex shape and angioscotomas compete for control of the local structure of OD columns. In the top row, the aspect ratio of the cortex is 1.5, whereas in the bottom row, it is 2.0. Each row is otherwise identical to Figure 4G–L, in which the aspect ratio of the cortex is 1.0. A–C, When the angioscotoma is introduced early in OD map development, the angioscotoma dominates local column structure. D, E, When the angioscotoma is introduced later in OD column segregation, the alignment of the OD columns (caused by the rectangular shape of the cortex) reduces the ability of the angioscotoma to cause a rearrangement in the cortex (compare with Fig. 4J,K). This effect becomes stronger with increasing alignment of the OD columns as seen by comparing Figure 4K with E (top and bottom rows). F, When OD columns are already well segregated before birth, there is no representation in the OD map, regardless of the shape of the cortex. OD maps were produced by holding l constant at 0.05 and changing the birth time K_b.

The final elastic net simulations (see Fig. 8) added orientation preference and selectivity dimensions. These dimensions were represented in polar coordinates by N_OR = 6 values of orientation preference arranged uniformly around a ring of radius r. The value of r relative to l dictates the timing of development of the OR map relative to the OD map (Hoffsümmer et al., 1995, 1996; Goodhill and Cimponeriu, 2000). For this set of simulations, a two-dimensional cortical net of 180 × 180 = 32,400 points was mapped to the training set of 50 × 50 × 2 × 6 = 30,000 feature points.

Figure 8.

Angioscotomas cause only slight changes to OR maps induced indirectly by the tendency for the OD and OR contours to intersect orthogonally. A–G, OR maps are shown as contour maps (contours in blue) and false-color maps in which intensity indicates strength of OR selectivity and color indicates OR preference according to the color code shown at bottom right. OD contours are overlaid in black or white. The crosses indicate the cortical locations of the feature points that are deprived after birth. The angioscotoma was introduced at birth time K_b, and annealing was continued at the same rate for 10 iterations after birth; a smaller K_b value corresponds to later birth (and hence angioscotoma introduction), when column formation is more advanced. A–C, OD columns form slightly before OR columns (l = 0.05; r = 0.07; see Materials and Methods). If the angioscotoma is introduced at an appropriate time to be represented in the OD map and the OR map has formed (B), then OR columns are affected indirectly by the angioscotoma, because they must arrange themselves in a way that maintains the tendency for the OD and OR contours to intersect orthogonally. E–G, OR columns form slightly before OD columns (l = 0.05; r = 0.075). If the OR columns have already formed and the angioscotoma is introduced at an appropriate time to be represented in the OD map (E,F), then the OD contours are more convoluted, because the OD columns must arrange themselves in a way that maintains the tendency for the OD and OR columns to intersect orthogonally. H, The small effect of the angioscotoma on the OR map in B can be seen when the OR contours of the map that develops with the angioscotoma (blue) are overlaid on the contours of the OR map that develops if the angioscotoma is not introduced (red). I, When a wider angioscotoma is introduced, the effect on the OR map is larger.

For all elastic net simulations, the net started from a random initial configuration with some global topographic bias. A continuity constant of β = 10 was used for all simulations. A coverage constant α = 1 was used for all nondeprived feature points, and α = 0 was used for deprived points (see below, Angioscotoma simulation). K was reduced (annealed) exponentially from a starting value of 0.2 at a rate of 0.9925 per iteration relative to the previous iteration.

In the Kohonen simulations (see Fig. 5), for each iteration a stimulus point (x, y, OD) was drawn randomly from a fixed training set, where x and y were each one of (N_x = N_y = 50) uniformly spaced points in [0,1] and OD was either −l or l. The cortex consisted of 64 × 64 points and started from a random initial condition with some global topographic bias. The rate constant was ε = 0.01, and K was annealed from 0.2 at a rate of 0.9999985 per iteration. Annealing had to be slower for the Kohonen simulations than the elastic net simulations, because only one stimulus point was presented at each iteration, so many more iterations were required to adequately sample the training set.

Figure 5.

Different degrees of angioscotoma representation similar to those observed experimentally (Fig. 1) are also produced in the two-dimensional cortices using the Kohonen algorithm by changing the ratio l/K_b, which controls how segregated the OD columns are at birth. For all simulations, at each iteration, a different stimulus was drawn randomly from a fixed set. The angioscotoma was introduced at K = K_b, and annealing was continued at the same rate for 10⁵ iterations after the angioscotoma introduction. This corresponds to each nondeprived retinal point being presented ∼20 times after angioscotoma introduction. Black represents afferents from one retina, and white represents afferents from the other.

Angioscotoma simulation.

Our simulations had two phases, one before visual experience and one after, as used by Berns et al. (1993). We began annealing from K = 0.2 and introduced a localized deprivation to one eye in the shape of a prototypical vascular tree (an angioscotoma) at K = K_b. The initial phase of annealing from K = 0.2 to K_b represents column development before visual experience. After the introduction of the angioscotoma at K_b, annealing continued at the same rate for 10 iterations for the elastic net and 10⁵ iterations for the Kohonen simulations, reflecting the fact that cortical maps remain plastic for only a finite period of time after birth (for review, see Hensch, 2004). Throughout this article, we use the terms “the onset of visual experience” and “birth” interchangeably to signify the point in the simulations after which selected feature points were deprived. No other changes were made to the correlational structure of the input at this point.

In the Kohonen simulations, for K < K_b certain points in the shape of a vascular tree were excluded from the training set from which a training point was randomly drawn at each iteration. In the elastic net simulations, our method of simulating an angioscotoma follows the method for modeling monocular deprivation used by Carreira-Perpiñán et al. (2005). In their study, maps initially developed with each feature point v_i having α = 1. To simulate monocular deprivation after some development, α was reduced from 1 to 0.4 for each feature point corresponding to the deprived eye. Here, α scales the strength of the influence that each feature point exerts on the elastic net. In our simulations of map development with an angioscotoma, in both eyes before birth and in the nondeprived eye after birth, α was 1 for all feature points v. To simulate an angioscotoma in one eye after birth, α was set to 0 for all feature points in a localized area of visual field in one eye for K < K_b. By completely removing the influence on the cortex of all feature points in that area, we effectively made the eye “blind” to that area of visual field. For the mapping of a one-dimensional cortex to one dimension of visual field and one of OD (see Figs. 2, 3), after birth α was set to 0 for two adjacent visual field points in one eye. For the two-dimensional cortex simulations (see Figs. 4, 6, 7, 8), after birth α was set to 0 for all feature points in the visual field of one eye in the shape of a prototypical vascular tree. Our simulations only consider retinal points receiving full visual input (α = 1) or no visual input (α = 0). In reality, some retinal areas are in partial shadow, and even cells in the full shadow of a blood vessel still have a small amount of visually evoked activity as a result of pupil movement, dynamic pupil size, and scattered and diffracted light (Adams and Horton, 2003b). Using a reduced but nonzero α = 0.4 for the deprived points did not change the results significantly. Our simulations of monocular deprivation (see Fig. 6, top row) follow the method used by Carreira-Perpiñán et al. (2005).

Results

The representation of angioscotomas in primary visual cortex was examined using two well established feature-mapping models of visual cortical development, the elastic net algorithm and the Kohonen algorithm (Erwin et al., 1995; Swindale, 1996). In the annealed version of these models, which we use here, the time course of development is primarily controlled by an annealing parameter K, which was gradually decreased during the simulation. To simulate map formation before the onset of visual experience, maps were allowed to develop for some time before the angioscotoma was included. At birth (K = K_b), the angioscotoma was introduced by removing the influence on the cortex of particular points in the visual field of one eye, in the shape of a prototypical vascular tree. This models points in one eye that receive no visual input. Map development was then allowed to proceed for a fixed interval, representing postnatal development. After this, maps were frozen, representing the end of the critical period for OD column plasticity (Hensch, 2004).

Angioscotoma representations in the one-dimensional elastic net

Although in reality the visual field and the cortex are two-dimensional, it is often instructive when modeling to first investigate a one-dimensional case (Goodhill and Willshaw, 1990; Wolf et al., 2000; Dayan, 2004). Figure 2 shows the mapping by the elastic net algorithm of a one-dimensional cortex to two one-dimensional rows of retinal points, one row representing each eye. The left column shows how the map develops when no angioscotoma is introduced, whereas the right column shows the same case with an angioscotoma. Note that the width of the angioscotoma representation in Figure 2F is approximately the width of the OD columns that are just starting to segregate. This result also occurred in the two-dimensional cortex simulations discussed later (see Figs. 4, 6).

Two key parameters introduced in Figure 2 are l and K_b. The parameter l is one-half the separation in feature space between the feature points in each eye (Fig. 2A) and can be related to the correlation between the eyes (Yuille et al., 1996). Increasing l both accelerates OD column formation and makes columns broader (Goodhill and Willshaw, 1990; Hoffsümmer et al., 1995, 1996; Goodhill and Cimponeriu, 2000). The parameter K_b is the value of the annealing parameter at the onset of visual experience; the smaller the K_b value, the longer maps have been allowed to develop before visual experience, so the more segregated OD columns are at birth. There are several possible biological sources of natural variation in l and K_b (see Discussion).

Figure 3 demonstrates that angioscotoma representations similar to those observed experimentally (Fig. 1) could be produced in two regimes for a deprivation of a fixed width. In the left column, the birth time K_b is constant for all simulations, and l changes, whereas in the right column, l is constant, and K_b changes. When the angioscotoma is introduced very early in column development (Fig. 3A), no OD columns are present and there is only a faint representation of the angioscotoma, because development continues for only a fixed interval after birth. In other simulations, as l increases or K_b decreases, the representation becomes increasingly darker, and frosting becomes evident (Fig. 3B,C). With additional increases in l or decreases in K_b, OD columns become increasingly segregated in the cortex surrounding the angioscotoma, and frosting becomes even more evident (Fig. 3D). Eventually, the angioscotoma representation and the frosting begin to blend in with the surrounding columns (Fig. 3E). Figure 3, F and G, shows that the angioscotoma has no representation at all in the cortex if it is introduced when column formation is well advanced. In particular, a representation of the deprived eye is still apparent in regions of cortex that one might have expected to be dominated by the nondeprived eye. This agrees with experimental observations (Adams and Horton, 2003b).

The fact that the experimental results could be reproduced in these two regimes demonstrates that a key variable in producing different degrees of angioscotoma representation in the cortex is how developed the OD columns are at the onset of visual experience. This is controlled by the ratio l/K_b; the larger this ratio is, the more developed OD columns are at birth. The ratio can be increased by reducing K_b (as done in the right column), which gives the OD columns more time to develop before birth, or increasing l (as done in the left column), which accelerates OD column formation. In our simulations, the degree of column segregation at birth is a key determinant of the degree of angioscotoma representation, and the correlation of degree of angioscotoma representation with OD column width is simply a byproduct of the positive correlation between the rate of column segregation and the final columnar width.

Angioscotoma representations in the two-dimensional elastic net

Figure 4 shows the mapping using the elastic net algorithm of a two-dimensional cortical net to two two-dimensional sheets of retinal points, one for each eye. In these simulations, the angioscotoma introduced at birth takes the shape of a vascular tree. Comparing Figure 4A–L with Figure 1C–F, we see that with a two-dimensional cortex, as with the one-dimensional cortex, the elastic net algorithm generates OD maps with different degrees of angioscotoma representation similar to the different degrees observed experimentally. Figure 4A–L shows two-dimensional extensions of Figure 3. As K_b or l is varied in different simulations, the segregation of OD columns at birth changes, and the angioscotoma representations follow the same pattern of being faint when the OD columns are not segregated before birth (Fig. 4A,G) but becoming more distinct with more apparent frosting when the angioscotoma is introduced later in development (Fig. 4B,H). When the angioscotoma is introduced while OD columns are segregating, we see a clear representation against a background of poorly segregated OD columns (Fig. 4C,D,I,J). In simulations in which the angioscotoma is introduced just after OD columns have formed, the angioscotoma representation is disrupted (Fig. 4E,K). The representation gradually disappears altogether when the angioscotoma is introduced when columns are increasingly crisply segregated (Fig. 4F,L).

OD maps generated by simulations differing only in the shape of the angioscotoma (Fig. 4K,M–O) demonstrate that the degree of angioscotoma representation is independent of the specific pattern of the angioscotoma, and the effects of angioscotomas are local. OD maps generated by simulations differing only in the random initial configuration of the elastic net (Fig. 4K,P–R) demonstrate that the degree of angioscotoma representation is independent of the specific pattern of OD columns.

Overall, Figure 4 demonstrates that in the two-dimensional cortex (as in the one-dimensional cortex), the degree of segregation of OD columns at the onset of visual experience is a key determinant of the degree of angioscotoma representation.

Angioscotoma representations in the two-dimensional Kohonen algorithm

We found that angioscotoma representations similar to the four types observed in squirrel monkeys can also be produced using the Kohonen algorithm (compare Figs. 1C–F, 5). As with the elastic net algorithm, the four types of representation could be produced in two different ways: by keeping the birth time K_b constant and changing the width of the columns l (Fig. 5, left column) or by keeping the column width l constant and introducing the angioscotoma at different times (Fig. 5, right column). Similarly to the elastic net, increasing l for constant K_b accelerates OD column formation and so also changes the timing of birth relative to OD column formation. Accordingly, as with the elastic net, the common variable between the two simulation regimes is how segregated the OD columns are when the angioscotoma is introduced, emphasizing again that this is a key determinant of the degree of angioscotoma representation.

The ability to reproduce the experimental results with both the elastic net algorithm, in which all stimulus points are presented simultaneously, and the Kohonen algorithm, which presents stimuli one at a time and uses a slightly different learning rule, demonstrates that the specific choices of training set and training regime are not critical to the basic phenomena we have observed. More generally, this provides additional evidence that the general principles of the competitive, Hebbian, feature-mapping class of models may capture some of the fundamental biological principles underlying OD column formation. Given the similarity of the results using the two algorithms, the rest of this article focuses on the elastic net algorithm.

Mechanism of different degrees of angioscotoma representation in the elastic net

The different degrees of angioscotoma representation generated by the elastic net can be explained for a fixed l in terms of the K-value at birth, K_b. K controls the degree of OD column segregation by altering the strength of the coverage and continuity terms. The coverage term describes the pull of the retinal points on the cortical points (Swindale, 1996). Each retinal point has a finite amount of influence that it shares out among all of the cortical points in its domain of attraction (Goodhill and Willshaw, 1990). The influence of each retinal point, described by the coverage term, falls off like exp(−d²/2K²) as we move a distance d from the retinal point, and is normalized. The form of this term means that when K is large, there is a gentle decrease in influence with d so that each retinal point influences many cortical points almost equally, causing cortical points to be binocular. As K decreases, the drop in influence with distance becomes steeper, so that each retinal point gives an increasing share of its influence to closer cortical points at the expense of more distant points. In general, the coverage term has the effect of narrowing the receptive fields of cortical cells to be more similar to the stimuli to which they are already most responsive (Swindale, 1996). K also weights the continuity term, which describes the “tension” in the cortical rope that tends to make the receptive fields of neighboring cortical cells similar to each other. As K decreases, the tension between cortical points decreases. Overall, as K slowly decreases, the attractive effect of the retinal points becomes localized, whereas the tension pulling cortical points together decreases, together allowing OD columns to form. Therefore, K_b is indicative of the degree of OD column segregation at birth. In the following discussion, we will arbitrarily consider an angioscotoma in the “top” eye as depicted in Figures 2 and 3.

If K_b is large (Fig. 3A, right column), then at birth all cortical points are binocular. When the angioscotoma is introduced, the missing influence of the deprived retinal points in the top eye gives the nondeprived retinal points in the bottom eye serving the same cortical area a competitive advantage. Consequently, the cortical cells in this area become more responsive to the nondeprived bottom eye. However, because K is still large, the nondeprived retinal points in the top eye still have a significant influence on many cortical cells and so partly compensate for the missing influence of the deprived retinal points. Also, the large weighting of the continuity term tends to keep the cortical rope straight. Overall, this means that angioscotoma introduction early in OD column development, when K is large, results in faint, thin angioscotoma representations. As K_b decreases, the coverage term becomes increasingly localized, reducing the compensatory influence of nondeprived retinal points in the top eye on cortical cells in the angioscotoma representation. The tension of the continuity term also decreases. Together, these altered forces mean that as K_b decreases, we see stronger angioscotoma representations (Fig. 3B–D, right column).

Frosting starts to appear as K_b decreases, because of the increasing localization of the coverage term. Because of the existing angioscotoma representation, retinal points in the bottom eye serving the edge of the representation have more cortical cells in closer proximity than retinal points in the top eye adjacent to the angioscotoma (Fig. 2B, right column). This means that as K decreases, the retinal points in the top eye adjacent to the angioscotoma have a increasingly dominant influence on cortical cells on the edge of the angioscotoma representation, leading to the frosting effect (Fig. 3B–D, right column). The mechanism described here is identical to the mechanism by which OD columns normally form in the elastic net when there are small random fluctuations from perfect binocularity; the initial OD column of the angioscotoma representation simply acts as a seed.

As K_b reduces further (Fig. 3E–G, right column), angioscotoma representations start to disappear, because the coverage term is highly localized, and the continuity term is weakened to an extent that OD columns are segregated to some degree before the angioscotoma is introduced. This means that before angioscotoma introduction, some cortical points have moved away from the horizontal midline, toward the to-be-deprived top retinal points. Because the influence of the retinal points is strongly related to distance for small K, this upward move means that the retinal points in the top eye adjacent to the angioscotoma exert a larger influence than retinal points in the bottom eye and can better compensate for the deprived retinal points, stopping cortical rearrangement in response to the angioscotoma.

The same reasoning for the different degrees of representation holds for increasing l (as done in Fig. 3, left column), because this increases the distance between the retinal points and the cortical points d. Because the influence of the retinal points falls off as exp(−d/2K²), increasing d is equivalent to decreasing K and has the same localizing effect on the coverage term. Decreasing K_b and increasing l are in this sense computationally equivalent.

Angioscotoma width and degree of representation

We also investigated whether the degree of representation is influenced by the ratio of angioscotoma width to OD column width, as proposed by Adams and Horton (2003b). Until now, we have presented simulations with relatively narrow angioscotomas. Figure 6 summarizes the variation in angioscotoma representation with the ratio of angioscotoma width to OD column width as well as OD column segregation at birth. Moving left to right in the figure shows how increasing OD column segregation at birth affects angioscotoma representation, whereas moving bottom to top in the figure shows the effect of increasing the ratio of angioscotoma width to OD column width. We examined the influence of angioscotoma width relative to OD column width by performing sets of simulations in which angioscotoma width was increased while l/K_b was constant (corresponding to moving purely vertically through Fig. 6). We found that although the ratio of angioscotoma width to OD column width did indeed influence the amount of rearrangement in the cortex, varying this parameter alone did not produce the different degrees of representation observed experimentally.

In general, increasing the width of an angioscotoma increases the visibility of its cortical representation but does not alter the type of representation. If no OD columns are present at birth, or they are just forming during the critical period (Fig. 6, blue and green regions), then increasing the width of the angioscotoma simply creates a stronger representation with stronger frosting. If the OD columns have already formed at birth (Fig. 6, red and yellow region), then increasing the width of the angioscotoma relative to the width of the OD columns results in more cortical territory being given over to the nondeprived eye. This allows a transition from no representation (Fig. 6, red region) to a disrupted representation (Fig. 6, orange region) if OD columns are well segregated at birth, but there still cannot be a transition to the other two states observed experimentally by varying the width ratio alone. To pass through the four regions of the phase diagram corresponding the four different types of representation observed experimentally (Fig. 6, blue, green, orange, and red regions), the segregation of the OD columns at birth must be varied by changing the width of the OD columns (Fig. 6, cyan lines), the time of birth (Fig. 6, yellow lines), or both. Note that in reality, the variability in representation forms a continuum but has been drawn as discrete regions for ease of explanation and understanding.

The fact that changing the width ratio alone cannot produce the four types of representation observed experimentally also follows more generally from the result that angioscotomas affect local map structure only. Experimentally, the degree of OD column segregation changes in register with the type of angioscotoma representation observed. Because the effects of angioscotomas are local, changing the relative width of an angioscotoma alone cannot create OD columns or stop them from forming over the whole primary visual cortex to produce the four types of maps observed experimentally.

There is a type of representation in Figure 6 that has not been observed experimentally: complete angioscotoma representation over the whole visual cortex, with well formed OD columns (Fig. 6P,U,AA,FF). This type of representation does not occur biologically, because the cortical magnification factor and blood vessel diameter both change with visual field position. This region of the phase diagram indicates that if the cortical width of the deprivation is sufficiently wide, there can be rearrangement of very well segregated columns. This is most likely to occur for vessels near the optic disc, because here the vessels are the widest and the cortical magnification factor is moderate (Adams and Horton, 2002).

Angioscotomas have a greater influence on the cortex as they get wider because the increased width reduces the ability of retinal points adjacent to the angioscotoma to compensate for the deprived retinal points. As explained in the previous section, if OD columns have started to segregate when a deprivation is introduced, then retinal points adjacent to the angioscotoma can compensate for the deprived retinal points, and there is no angioscotoma representation (as in Fig. 6, red region). However, if a wider angioscotoma is introduced instead, there are more deprived retinal points to compensate for, and some of those points are farther away. Because the attractive influence of retinal points described by the coverage term is normalized and is strongly related to distance, as deprivation gets wider, the retinal points adjacent to the angioscotoma lose their ability to compensate, particularly for retinal points at the center of the deprivation. As a result, there is some cortical rearrangement in response to the angioscotoma (Fig. 6, orange and yellow regions). As the deprivation gets wider, the OD columns must be increasingly well segregated at birth for there to be no angioscotoma representation.

The cortical widths of the angioscotoma representations at the different stages of OD column segregation are in agreement with the experimental observations of Adams and Horton (2003b). If the OD columns have not segregated at birth, then angioscotoma representations are approximately the cortical width of the deprivation (Figs. 3A–C, 6, blue region). However, if the OD columns have started to segregate at birth, then any cortical representation of an angioscotoma is at least as wide as the OD columns, even if this is wider than the cortical width of the deprivation (Figs. 3D,E, 6, green, orange and yellow regions); narrow angioscotoma representations through wide OD columns are never seen. The “enhanced width” seen in Figure 3, D and E, and Figure 6, C–E, I, and J, was observed in the angioscotoma representations of squirrel monkeys with fine or intermediate OD column segregation and width (Adams and Horton, 2003b). The model also predicts that any frosting of angioscotoma representations is approximately the width of the OD columns, even in individuals in which the representation is wider than the average OD column width (Fig. 6Z,AA,EE,FF).

For comparison, the top row of Figure 6 models complete monocular deprivation by extending the deprived area to cover an entire eye. Comparing Figure 6, F and KK, we see that complete monocular deprivation may still have an effect on cortices with OD columns that are too developed at birth to see an angioscotoma representation.

Interaction of angioscotomas and cortex shape

It can be seen in Figures 3–6 and in the original results of Adams and Horton (2003b) (reproduced here in Fig. 1) that in certain parameter regimes, angioscotomas exert a strong influence on local column structure. How do the local representations of angioscotomas interact with more global influences on column layout in visual cortex? Several influences on global layout have been examined previously (Goodhill et al., 1997; Yu et al., 2005), including cortical shape (Jones et al., 1991; Goodhill and Willshaw, 1994; Bauer, 1995; Wolf et al., 1996). In particular, it is known that when two square visual fields map to a rectangular cortex, columns tend to align parallel to the short axis of the cortex (Jones et al., 1991; Goodhill and Willshaw, 1994; Bauer, 1995; Wolf et al., 1996; Goodhill et al., 1997). We simulated this again, but now in the presence of an angioscotoma in one eye. Figure 7 shows the results of simulations with the same parameters as those used in Figure 4G–L but with a rectangular rather than square cortex. It is apparent that the influence of the angioscotoma dominates locally when it is introduced early in OD map development (Fig. 7A–C), overcoming the tendency for columns to align parallel to the short axis, but that the aspect ratio of the cortex regains control of local as well as global OD column structure when the angioscotoma is introduced later in OD map development (Fig. 7D,E). Comparing Figure 7E with Figure 4K, it is especially evident that the angioscotoma causes increasingly less rearrangement of the OD pattern as the predisposition for the OD columns to flow in a different direction becomes stronger.

Influence of angioscotomas on orientation maps

Can angioscotomas affect the structure of OR maps in the primary visual cortex, and if so, how? OR map structure is known to be strongly coupled to OD map structure; for instance, OD and OR map contours tend to intersect orthogonally (Bartfeld and Grinvald, 1992; Obermayer and Blasdel, 1993, Hübener et al., 1997; Kim et al., 1999). This is reproduced by both the elastic net (Carreira-Perpiñán et al., 2005) and Kohonen algorithms (Erwin et al., 1995; Swindale, 1996).

Figure 8 extends the elastic net simulations in Figure 4I–K to include OR as well as OD maps. These simulations reveal that angioscotomas cause only very slight changes in OR maps. The small changes are induced indirectly by the tendency for OR contours to intersect orthogonally with OD contours (which are affected directly by the angioscotoma). Analysis of intersection angles showed that this tendency for orthogonal intersection is not reduced by the presence of angioscotomas (data not shown). Because the (very small) effects on OR maps are indirect, they only occur when OR columns form after OD columns and when the angioscotoma is introduced at an appropriate time to be represented in the OD map (Fig. 8B,H,I). The effect on local OR map structure in this situation is demonstrated in Figure 8H, in which the OR contours of the map that develops with the angioscotoma as shown in Figure 8B (blue contours) are overlaid on the contours of the OR map that develops if the angioscotoma is not introduced (red contours). When a wider angioscotoma is introduced, the effect on the OR map is larger (Fig. 8I). If OR columns form before OD columns, the tendency for orthogonal intersection causes any angioscotoma representations in the OD maps to be more convoluted at the contour edges (Fig. 8F,G).

Angioscotomas do not have a significant direct effect on the (binocular) OR map, because in the area of the angioscotoma, all orientations still receive some input from the nondeprived eye, and all orientations are deprived equally, so no one orientation enjoys a competitive advantage. A negligible effect of angioscotomas on OR maps is nonetheless noteworthy, because OR maps are more likely to be functionally relevant than OD maps.

Discussion

We have shown that competitive, Hebbian, feature-mapping computational models of visual cortical development can reproduce recent experimental data regarding the representations of angioscotomas in the primary visual cortex of squirrel monkeys (Adams and Horton, 2002, 2003b). The ability of both the Kohonen and elastic net models to reproduce the experimental results and the insensitivity of the results to whether batch or online learning is used, or whether stimuli are drawn from a fixed or continuous set, is additional evidence that the competitive, Hebbian, feature-mapping models capture the essential biological principles underlying OD column formation.

This study sheds light on the factors controlling the degree of angioscotoma representation in V1. Adams and Horton (2003b) discussed the idea that this could be influenced by the width of OD columns relative to the width of the angioscotoma. We have shown that, although this ratio does have some influence on angioscotoma representation, it is not the primary determinant of the degrees of representation observed experimentally. Rather, the simulations presented here suggest that the degree of OD column segregation at the time of birth is a critical factor in determining the degree of angioscotoma representation and that the correlation with OD column width is partly a byproduct of this. In the elastic net, OD column periodicity and the time course of OD development are both controlled by the same parameter l, and the model predicts that columns that develop faster should be wider, whereas those that develop slower should be narrower (Hoffsümmer et al., 1995, 1996; Goodhill and Cimponeriu, 2000). We therefore propose that natural variability in the degree of OD column segregation at birth in squirrel monkeys could be an important biological variable determining the degree of angioscotoma representation.

That the degree of OD column segregation at birth might be important in angioscotoma representation was discussed by Adams and Horton (2003b) but was considered unlikely because of experiments on the macaque. LeVay et al. (1980) showed that OD columns can locally remodel for weeks after birth in macaques despite the presence of wide, well segregated columns at birth (Horton and Hocking, 1996a). This suggests that the absence of angioscotoma representations in macaques (Adams and Horton, 2003b) is not a result of OD columns being well segregated at birth as we propose. However, in their study, LeVay et al. (1980) used monocular deprivation to test the ability of the cortex to remodel. We have demonstrated here that in the elastic net, the global deprivation of monocular deprivation still produced rearrangement of the OD map when introduced at segregation levels when an angioscotoma has no effect (as seen by comparing Fig. 6F, KK). Therefore, the fact that macaque cortex is influenced by monocular deprivation at birth does not necessarily mean that it should also be influenced by an angioscotoma. The presence of well segregated OD columns at birth in macaques has also been proposed (Adams and Horton, 2006) as a reason for why one should not expect to see any effect of strabismus in the macaque. Studies examining when OD columns form in squirrel monkeys with different column widths would help verify or disprove our hypothesis.

Variability in rate of OD column segregation could be a cause of different degrees of OD column segregation at birth. It is known that final column width is highly variable (Horton and Hocking, 1996b; Adams and Horton, 2003a), which in itself implies variability in rate of segregation in our model, because of the coupling of stripe width and rate of segregation. That images of OD columns at birth in macaques show similar degrees of segregation (Horton and Hocking, 1996a) can be explained by positing that segregation is already well advanced in all of these cases, and one would have to look at an earlier time point to detect differences in rate of segregation. What biological factors might cause natural variability in the rate of OD column segregation? First, there might be intrinsic differences in the overall amount of spontaneous activity present in retinal waves (Meister et al., 1991; Warland et al., 2006). Second, there might be varying degrees of thalamic coupling between retinally generated activity in the two eyes (Weliky and Katz, 1999). Thirdly, there might be cortex-wide differences in rates of synaptic plasticity, perhaps ultimately related to the rates at which animals learn postnatally (Adams et al., 2001). Individual differences in all of these parameters must clearly exist; what is currently unknown is whether these differences are large enough to explain the differences we hypothesize in the rate of OD column development.

Apart from differences between individuals in rates of OD column development, differences in gestation length could also contribute to interindividual differences in the degree of OD column development at the onset of visual experience. It is known that gestation length in squirrel monkeys is highly variable, with values from studies using reliable methods to assess the date of conception ranging from 137 to 175 d (Goss et al., 1968; Jarosz et al., 1977; Kerber et al., 1977; Stolzenberg et al., 1979). There are some suggestions that gestation length in squirrel monkeys may be more variable than in other primates and that this may be linked to the fact that births are synchronized within squirrel monkey groups (Boinski, 1987; Hartwig, 1996). However, macaques also have a variable gestation length, reported to range from 133 to 200 d (Silk et al., 1993). Nonetheless, the fact that the duration of gestation in macaques is longer on average, together with our proposal that OD column development is faster (inferred from the fact that macaques have wide OD columns), may mean that the onset of visual experience and angioscotoma introduction in all macaques occurs too late in OD column development for angioscotomas to be represented in the cortex, despite the variability in gestation length.

Our results also show that alignment of columns along one axis as a result of the shape of the cortex reduces the ability of angioscotomas to influence the local structure of OD maps when the angioscotomas are introduced during OD column segregation. This may contribute to the variability in angioscotoma representations observed experimentally and illustrates how different factors can interact when influencing the structure of OD maps.

We have shown that our results hold for the competitive, Hebbian, feature-mapping class of models. It would be interesting to extend the results to other models of OD map development such as the high-dimensional elastic net and Kohonen algorithms (Obermayer et al., 1990) and correlation-based models (Linsker, 1986; Miller et al., 1989). Because all of these models are based on similar basic principles (Yuille et al., 1996), it is likely that they could be adapted to reproduce the results presented here and perhaps provide additional insight into the biological mechanisms underlying variability in angioscotoma representation.

OD maps appear to be unique to each individual (Hubel and Wiesel, 1977; Horton and Hocking, 1996b; Adams and Horton, 2003a,b; Kaschube et al., 2003). Although angioscotomas only affect local OD map structure, variability in angioscotoma representations in squirrel monkeys is still one of the many factors that help make each map unique. We have shown that in competitive Hebbian models, several different parameters influence to what degree angioscotomas are represented in the cortex, and there are many possible biological causes of variation in these parameters. It could be that rate of column segregation, gestation length, and cortex shape in squirrel monkeys have coincidentally appropriate ranges to not only allow angioscotoma representations but also allow different degrees of representation. Overall, our examination of angioscotoma representations illustrates how different factors can interact to influence the structure of OD maps and provides insight into the complex, interrelated causes of the variability in OD maps that makes each OD map unique.