Figure 7.
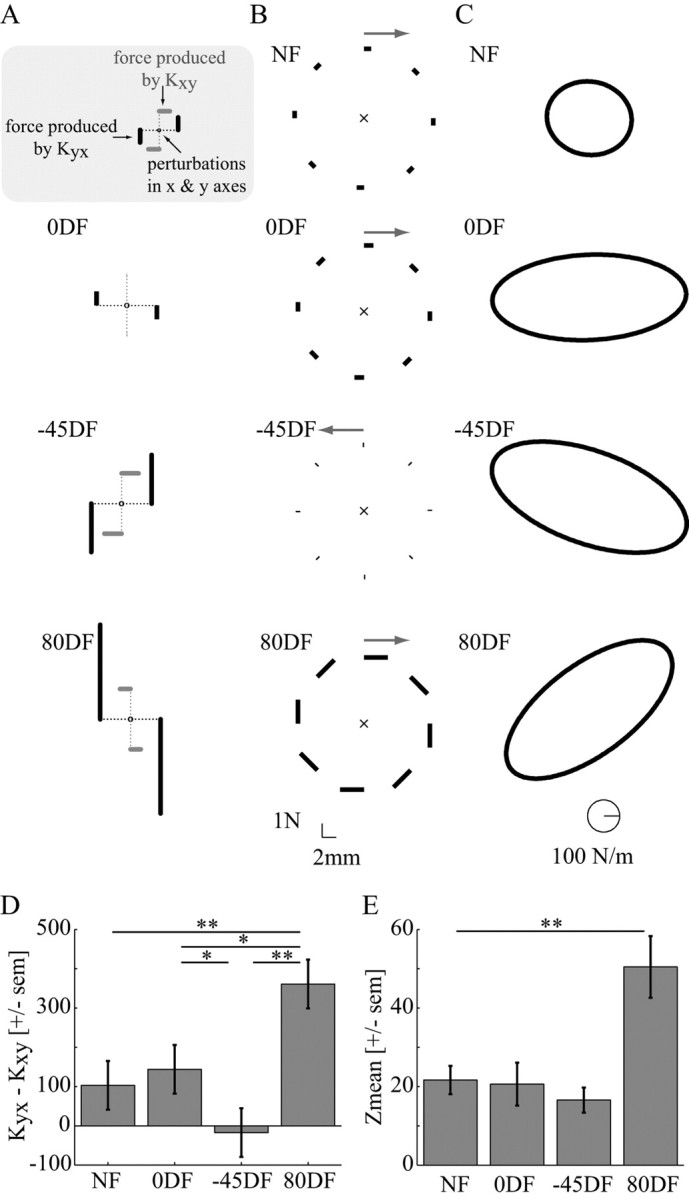
Symmetric and antisymmetric components of endpoint limb stiffness. A, Effect of the change in cross-terms of the endpoint stiffness matrix (Kxy and Kyx). For each of the three divergent force fields, the resulting change in the cross-terms relative to the original NF stiffness was calculated. The force (solid line) resulting from a 1 cm displacement (dotted line) was calculated for each of the ΔKxy (gray) and ΔKyx (black) terms. The Kxy terms after adaptation were not significantly different from the NF values and produced only small changes in force. Although the ΔKyx did not produce large forces in the 0DF field, it produced opposite effects in each of the −45DF and 80DF fields. These forces were directed to resist the oppositely directed forces from the divergent force field. B, The mean antisymmetric components of the limb stiffness for all four force fields. The force created by the antisymmetric component in response to a 10 mm displacement is displayed for eight equally spaced directions (calibration shown at the bottom). At the top of each figure, an arrow displays the direction of this curl component. C, The mean symmetric endpoint stiffness for each of the four force fields. The calibration is shown at the bottom of the figure. D, The difference in the cross-terms of the stiffness matrix (Kyx − Kxy) is shown after adaptation to each force field. It is this difference that gives rise to the antisymmetric components of the endpoint stiffness. Statistics indicate the results of Tukey's HSD post hoc test. (*p < 0.05; **p < 0.001). E, The relative contribution of the antisymmetric component of the endpoint stiffness compared with the overall symmetric forces. The Zmean and SEM are shown for each of the four force fields. Statistics indicate the results of the Dunnett's t post hoc test testing the difference of each group from the NF results (**p = 0.001).
