Adjustment for urinary creatinine or serum lipids for analytes assayed in pooled specimens

Abstract

Background:

For case–control studies, pooling biologic specimens (cases with cases and controls with controls) can make it affordable to study a biomarker that is expensive to assay, while conserving quantities of archived specimens. For a fixed number of participants, pooling designs incur little loss of estimation precision, and they can even improve precision by enabling inclusion of more participants with the same number of assays. A limitation that has discouraged the use of these methods in environmental epidemiology, however, is the lack of a valid way to adjust for creatinine (urinary dilution) when assaying a biomarker in urine or to adjust for serum lipids when assaying a lipophilic biomarker in serum.

Objective:

We aimed to develop practical strategies to accomplish those adjustments.

Methods:

Our strategies either differentially dilute specimens before pooling equal aliquots or, alternatively, pool deliberately unequal aliquots from each specimen, where prior determinations of the adjustment factor in each individual specimen inform their differential dilution or unequal aliquot volumes. In addition, we show how to modify these strategies if, instead of just adjusting for creatinine per se, one needs to account for factors that influence creatinine. We carry out simulations under several causal scenarios.

Results:

We demonstrate that the proposed strategies perform well in estimating the same adjusted association parameter as would be estimated by using individually-assayed specimens.

Conclusion:

By implementing the proposed strategies when forming specimen pools, one can greatly improve the efficiency of case–control studies that involve an expensive-to-assay exposure measured in biospecimens.

Introduction

Specimen pooling is an efficient and cost-effective design strategy for case–control studies when a quantitative assay is expensive or when quantities of archived specimens are dwindling. In its simplest implementation, one randomly partitions the cases (controls) into multiple case (control) pooling sets. For each pooling set, one combines equal aliquots from the individual specimens and assays the resulting pool. Data analysis based on the pooled sets of specimens proceeds via logistic regression where the exposure variable is the measured concentration in the pooled specimen times the number of specimens in that pooling set, which approximates the sum of the specimen-specific concentrations based on measuring the pool ^1,2. The resulting estimates of risk parameters are valid under the generally plausible assumption that the concentration in the pooled specimen approximates the average of the concentrations in the individual specimens that contributed to the pool. Pooling offers several advantages. It reduces assay costs and conserves irreplaceable biospecimens. Also, because measures of pools are pulled toward the mean, pooling can markedly reduce the fraction of determinations that fall below the assay limit of detection. For a case–control study (matched or unmatched) that is analyzed by logistic regression, little power or precision is sacrificed when pooling sets are smaller than 10 ^2,3.

One important practical limitation to pooling has been the lack of strategies for standardizing pool-based analyte measures for creatinine or total lipids. When urine specimens are assayed, traditionally one would adjust the measured analyte level for urinary diluteness by dividing by urinary creatinine; correspondingly, when serum specimens are assayed for a lipophilic analyte, one would adjust for fat content of the blood by dividing by a measure of total serum lipids. The corresponding exposure variable entering a logistic regression model for individual specimens would then be a ratio of concentrations: analyte to creatinine for urine, or analyte to total lipid for serum. For pooled specimens, a statistically valid analysis would require the sum of the specimen-specific ratios for each pooling set as the exposure variable for that set (Weinberg and Umbach 1999). Because the ratio of two sums is generally not the same as the sum of the corresponding constituent ratios, naively adjusting a pool-based analyte concentration by dividing by the corresponding pool-based measure of creatinine or of serum lipids biases the risk parameter estimates, as we will show, compared to what one would expect with individual assays.

To provide some background, the best approach to adjustment when analytes are measured individually has been a matter of some controversy ⁴. In earlier work we considered directed acyclic graphs (DAGs) that represent the use of proxy measures of exposure (e.g. using urine or blood specimens) and showed via simulations that approaches based on classical division provide confidence intervals with nominal coverage but that those classical methods can sometimes be improved with modeling strategies ⁵.

We here extend those remedies for the standardization problem to settings where pool-based approaches are to be used, presuming that creatinine or serum lipid measurements are available for each individual specimen before pooling. Ideally, small aliquots for this purpose would be set aside at collection and frozen. Because we presume those assays are much less expensive than the assay for the primary analyte, that requirement is not very restrictive. Suppose all cases and controls have been partitioned into non-overlapping pooling sets and the plan is to pool together specimens within each set and assay the resulting pools. Our remedies involve modifying the construction of pools in ways that depend on the individual creatinine or lipid levels, either by variously diluting the specimens before pooling equal aliquots from each or, instead, by including unequal aliquots into the pool. First, we show that these strategies enable the use of traditional ratio standardization for creatinine or serum lipid with pooled assays. We then show that the covariate-adjusted standardization methods proposed by O’Brien et al. ⁵ can be applied via straightforward modifications to our proposed pooling strategies. To assess the performance of our proposals compared to no pooling and to the naive approach that relies on pooling equal volumes of specimens and adjusting based on the creatinine or serum lipid concentrations measured in the pool, we provide simulations of case–control studies under selected causal scenarios represented by DAGs ⁶. We focus primarily on the scenarios considered previously and use the statistical approaches identified previously as performing best ⁵. We conclude with some cautions.

Methods

Construction of pools

We consider first urinary analyte concentrations, with creatinine concentration providing the measure of diluteness. Suppose a pooling set comprises specimens from K cases or K controls. Suppose (Z₁, C₁), ⋯, (Z_K, C_K) are pairs of concentrations, where the C_j is the creatinine concentration and Z_j is the primary analyte level for specimen j. By regarding any pair (Z_j, C_j) as equivalent in exposure to (aZ_j, aC_j) for a > 0, traditional standardization takes $\frac{Z_j}{C_j}$, the value of Z per unit of C, as the dilution-adjusted exposure of interest for individual j.

Our primary goal was to develop pooling protocols that enable estimation of the sum of the analyte-to-creatinine ratios for each pooling set. The key is to allow the specimen-specific creatinine concentrations to inform the construction of pools. Two distinct protocols accomplish our goal: (1) unequally dilute the specimens and combine equal volumes of the diluted specimens; or (2) form each pool using unequal volumes from its component specimens.

Just-add-water protocol:

Let the most dilute specimen be indexed by j = 1. This protocol calls for adding an appropriate inert substance (e.g., distilled water) to multiply the volume of each specimen j by the factor C_j/C₁. Every specimen in the pooling set then has concentration C₁. Thus, dividing the measured analyte level in the resulting pool by C₁ and multiplying the quotient by K provides the required sum of analyte-to-creatinine ratios of specimens in the pool (Appendix A). This sum of ratios is the exposure variable needed for traditional creatinine standardization in a pooling-set-based logistic regression analysis. Adjustment for total serum lipids would proceed analogously.

Unequal-volumes protocol:

Alternatively one can form the pools using unequal volumes, where the volumes are specified in a way that depends on the C_j. Choose a reference specimen, indexed by j = 1, whose creatinine concentration is near the median for the pooling set. Let V₁ be the volume contributed to the pool by that reference specimen. Then each other specimen, j = 2, ⋯ , K, should contribute a volume of $V_j={}^{V_1{C}_1}/_{C_j}$. Thus, specimens with higher creatinine concentrations contribute proportionally smaller volumes. One way to think about this protocol is that instead of combining equal volumes from each specimen, one combines volumes that contain equal amounts of creatinine (V₁C₁ = V_jC_j by construction). As shown in Appendix B, the analyte concentration for that pooled specimen, denoted Z_M, is

$$Z_M={}^{\sum _{j=1}^K\left(\frac{Z_j}{C_j}\right)}/_{\sum _{j=1}^K\left(\frac{1}{C_j}\right)}.$$

Thus, to get the exposure variable needed for logistic regression based on pooling sets with creatinine adjustment, namely, ${\sum }_{j=1}^K\left(\frac{Z_j}{C_j}\right)$, one multiplies that analyte concentration by ${\sum }_{j=1}^K\left(\frac{1}{C_j}\right)$.

Covariate-adjusted standardization:

Certain factors may influence creatinine (or serum lipids). Such factors could also affect disease risk. O’Brien et al. ⁵ introduced the idea of using such factors for “covariate-adjusted standardization.” Briefly, one fits a preliminary regression model with creatinine as the outcome and any relevant stable factors, e.g., age, sex, as predictors. Using that model, one estimates the expected creatinine level, denoted E[C_j], and then calculates the ratio of the observed to the expected creatinine level, that is, $R_j=\frac{C_j}{E[C_j]}$. The rationale is that this ratio might provide a better adjustment for dilution than would C_j alone. The fitted risk model for individual specimens then uses the covariate-adjusted exposure $\frac{Z_j}{R_j}$.

To implement covariate-adjusted standardization when pooling specimens, the preliminary regression to predict creatinine is carried out before pooling. The creatinine-adjusted exposure variable used in logistic regression is now the sum of the creatinine-adjusted exposures for the individual specimens in the pool, namely, $\sum \frac{Z_j}{R_j}$. These exposure variables are measured by using either the just-add-water method or the unequal-volumes method to form the pooled specimens, but employing R_j in place of C_j. (Arguments analogous to those in Appendices A and B are valid provided one replaces all of the C_j throughout with R_j.) The just-add-water protocol takes as the reference specimen the one with the smallest R_j in the set; the unequal-volumes protocol instead chooses a reference specimen with an R_j value near the middle of those in the pooling set.

Simulation Methods

We carried out simulations to assess the performance of our approaches for pooling and for adjustment in various causal scenarios. Though our pooling protocols are operationally distinct, they both deliver the sum of standardized exposure levels needed for fitting pool-based models. Thus, our simulations do not distinguish between the just-add-water and unequal-aliquot protocols. We compare our pooling strategies to equal-volume pooling of undiluted specimens with adjustment based on creatinine measured in the pool (“naïve standardization”) and to analyses using individual specimens.

Causal Scenarios:

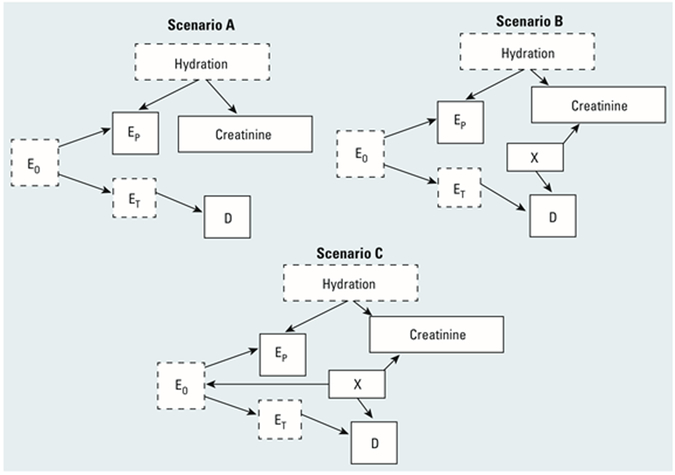
For biomarkers in urine, we studied causal scenarios A, B, and C of O’Brien et al. ⁵ (Figure 1) plus two added scenarios, B’ and C’. In scenario A, creatinine is only affected by recent consumption of water and the exposure is assessed by proxy using the adjusted level of a biomarker in urine, where the unmeasured risk-relevant exposure is exposure at a target tissue. Scenario B allows for a measured factor X that influences both creatinine and disease directly, and scenario C allows factor X to also influence the exposure itself. Our new scenarios B’ and C’ are like Scenarios B and C except that factor X has no direct effect on disease.

Figure 1.

Directed acyclic graphs showing scenarios where a proxy for an exposure biomarker is measured in urine, showing causal relationships among overall exposure concentrations (E₀), target tissue exposure concentrations (E_T), urinary (proxy) exposure concentrations (E_P), hydration, creatinine concentration, covariate X, and disease (D). Variables with solid outlines are observed; those with dashed outlines are unobserved. (Environ Health Perspect 2016; 124(2):220-227, https://ehp.niehs.nih.gov/1509693/.)

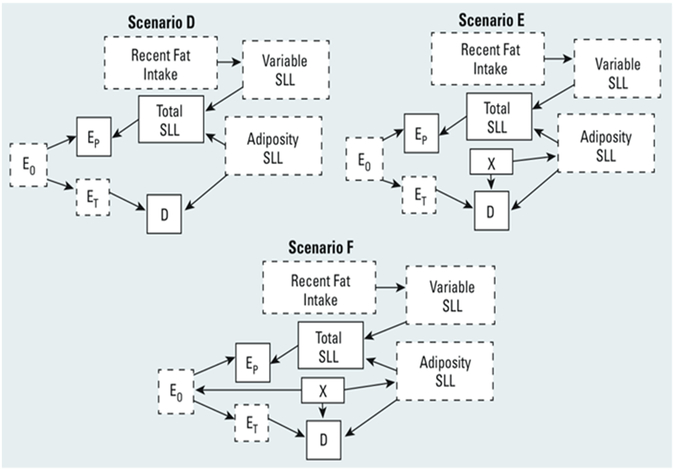
For lipophilic biomarkers measured in serum, we simulated causal scenarios D, E, and F of O’Brien et al (Figure 2) plus two additional scenarios, E’ and F’. The scenarios for serum are conceptually similar to those for urine but with features attuned to lipophilic biomarkers. Our new scenarios E’ and F’ resemble Scenarios E and F, except that factor X is not a cause of the disease.

Figure 2.

Directed acyclic graphs showing scenarios where a proxy for a lipophilic exposure biomarker is measured in serum, showing causal relationships among overall exposure concentrations (E₀), target tissue exposure concentrations (E_T), serum (proxy) exposure concentrations (E_P), recent fat intake, total serum lipid levels (SLL), variable SLL, adiposity SLL, , covariate X, and disease (D). Variables with solid outlines are observed; those with dashed outlines are unobserved.

(Environ Health Perspect 2016; 124(2):220-227, https://ehp.niehs.nih.gov/1509693/.)

Note that our scenarios do not measure the risk-relevant exposure -- an issue that exists whether one pools the biospecimens or not. In evaluating the behavior of our proposed adjustment approaches, we sought to compare an analysis using pooled specimens with what would have been seen using individual specimens. The mean difference in those estimates defines our “bias”.

Models fitted:

O’Brien et al. ⁵ investigated seven models that adjust for creatinine or serum lipids for each of six causal scenarios. For biomarkers in urine under scenarios A, B, and C, O’Brien et al. recommended their models 3 and 7 as best overall, but we consider only the more parsimonious model 3, which just uses covariate-adjusted standardization (Table 1 of O’Brien et al.). For fitting data for lipophilic biomarkers in serum under scenarios D, E, and F, O’Brien et al. recommended their models 2 and 6 as best overall; but we considered only the more parsimonious model 2, which uses traditional standardization (Table 1).

Table 1:

Predictors employed when comparing individual-specimen analyses, pooled-specimen analyses with naïve standardization after equal-volume pooling, and pooled-specimen analyses with standardization based on either the just-add-water or unequal-volumes protocols.

Standard- ization	Causal Scenarios	Individual-specimen analysesa		Pooled-specimen analysesb
				Naïve standardization		Proposed methods
		Exposure Variable, S	Covariates, X	Exposure Variable, SP	Covariates, XP	Exposure Variable, SP	Covariates, XP
Creatinine (covariate-adjusted)	A	$\frac{Z}{R}$	none	$K\frac{\sum Z_j}{\sum C_j}$	none	$\sum \frac{Z_j}{R_j}$	none
	B, B’, C, C’	$\frac{Z}{R}$	X	$K\frac{\sum Z_j}{\sum C_j}$	$\sum X_j$	$\sum \frac{Z_j}{R_j}$	$\sum X_j$
Total Lipid (traditional)	D	$\frac{Z}{C}$	none	$K\frac{\sum Z_j}{\sum C_j}$	none	$\sum \frac{Z_j}{C_j}$	none
	E, E’, F, F’	$\frac{Z}{C}$	X	$K\frac{\sum Z_j}{\sum C_j}$	$\sum X_j$	$\sum \frac{Z_j}{C_j}$	$\sum X_j$

Note: Causal scenarios are defined in Figures 1 and 2 (scenarios with primes (‘) eliminate the causal arrow from X to D in the corresponding un-primed scenarios); notation is defined in the text.

^a

Equation fitted in analyses of individual specimens:

$$\frac{\mathrm{Pr}[\mathit{case}\mid S,X]}{\mathrm{Pr}[\mathit{control}\mid S,X]}=\mathit{exp}\{\mu +\beta S+\alpha X\}$$

^b

Equation fitted in analyses of pooled specimens:

$$\frac{\mathrm{Pr}[\mathrm{case}\mathrm{set}\mid K,S_P,X_p]}{\mathrm{Pr}[\mathrm{control}\mathrm{set}\mid K,S_P,X_p]}=\mathit{exp}\{{\mu }^{\ast }K+\beta S_P+\alpha X_p+\ln (r_K)\}$$

To select models for our new scenarios (B’ and C’ for biomarkers in urine; E’ and F’ for biomarkers in serum), we compared traditional standardization with covariate-adjusted standardization. These preliminary simulations used only individual measurements, and the procedures closely mimicked those in O’Brien et al. (eAppendix 1: Model Selection for Scenarios B’, C’, E’, and F’). Results of these preliminary simulations echoed the results of O’Brien et al. in that covariate-adjusted standardization was better for scenarios B’ and C’, whereas traditional standardization was better for scenarios E’ and F’ (eTables 1 and 2 and eFigure 1).

Based on those results, when fitting models to the simulated data from pooled specimens, we used covariate-adjusted standardization of exposure for all five scenarios involving urine but used traditional standardization for all five scenarios involving serum. To account for pooling, the logistic models for pooled specimens use as predictors the sums of the corresponding predictors for individuals in each pooling set. Thus, as in Weinberg and Umbach ^1,2, we fit the following set-based logistic model, where K_p is the pool size, S_p is the sum of the model-relevant analyte-to-creatinine ratios for specimens in the pooling set ($\sum \frac{Z_j}{c_j}$ for traditional standardization; $\sum \frac{Z_j}{R_j}$ for covariate-adjusted standardization; $K_p\frac{\sum Z_j}{\sum c_j}$ for naïve standardization), and X_p is a covariate that equals the sum of the individual X values for members of the pooling set:

$$\frac{\mathrm{Pr}[\mathrm{case}\mathrm{set}\mid K_p,S_p,X_p]}{\mathrm{pr}[\mathrm{control}\mathrm{set}\mid K_p,S_p,X_p]}=\mathit{exp}\{{\mu }^{\ast }{K}_p+\beta S_p+\alpha X_p+\text{ln}(r_K)\}$$

Where r_K denotes the number of case sets of size K_p divided by the number of control sets of size K_p and the natural log of that ratio is included in the model as an “offset”, i.e., a covariate with a coefficient that is constrained to be 1. Note that the β in this model is the same as that in an individual-based model for risk.

Generating simulated data:

Our general strategy for generating pooled data was as follows. We first simulated predictors and outcomes for individuals in a case–control study under one of the causal scenarios using an assumed risk model. Then we randomly partitioned the cases into case pooling sets and the controls into control pooling sets.

The models we used were taken directly from O’Brien et al. ⁵, except that we did not transform exposure variables to their z-scores. Briefly, we first randomly generated covariates based on their corresponding distributions and position in the causal scenario. We generated values for independent covariates first; then values for covariates that depended on other covariates. For example, we generated hydration level before generating creatinine level. We then generated a person-specific probability of disease based on the assumed risk model (as in O’Brien et al.), randomly drawing case status from a Bernoulli distribution with probability given by the person’s disease risk. We kept simulating data until reaching the desired number of cases and of controls.

Performance evaluation:

In generating simulated data, we specified a risk parameter (β coefficient) for the exposure at the target tissue. The models that we fit, because they use the estimated proxy exposure in urine or serum after standardization, do not estimate β itself but, instead, estimate, say, β*. We need to know the β* for unpooled analysis to evaluate bias and confidence interval coverage. To calculate β* for each scenario, we simulated a data set of 1 million cases and 1 million controls and fit a model using the proxy standardized exposure. The estimated coefficient from fitting this model closely approximates the asymptotic value of β* for the proxy exposure when specimens are individually assayed.

In our simulations, we evaluated confidence interval coverage (proportion of simulated data sets where the confidence interval for β* covered β*), the bias (the mean difference between the estimates from each simulated data set and β*), and the power for assessing the effect of the analyte (proportion of simulated data sets where the 95% confidence interval failed to cover 0). We consider a pooling strategy to be valid if a model fit using the proxy standardized exposure derived from pools estimates the same risk parameter that a comparable analysis based on a proxy standardized exposure derived from individual specimens would have estimated. That said, because the sample size is smaller with pooling and logistic regression is itself necessarily biased (away from the null), except for large samples⁷. Thus, under alternatives to the no-effect null, some bias away from the null is expected.

Scope of simulations:

For biomarkers in urine, we studied five causal scenarios A, B, B’, C, C’ (Figure 1); similarly, for lipophilic biomarkers in serum, we studied five causal scenarios D, E, E’, F, F’. For each causal scenario, we simulated data using five different values for the effect of a unit change in the (unmeasured) exposure at the target tissue; we used odds ratios 2, 1.3, 1.0, 0.77, and 0.5, which correspond to logistic regression coefficients (β) of 0.69, 0.26, 0, −0.26, −0.69, respectively. For constructing power curves (shown in the online supplement), we included additional β values: 0.10, 0.14, 0.16, 0.18, and 0.22. We set pool sizes to 1, 2, 5, or 10, where 1 corresponds to individual specimens. For each of these 200 distinct data-generation scenarios, we simulated 1000 case–control studies, each with 500 cases and 500 controls. We fit logistic models as specified in Table 1. Models for pooled analyses with urine-based biomarkers used either naïve standardization after equal-aliquot pooling or covariate-adjusted standardization following our proposed pooling strategies. Models for pooled analyses with serum-based biomarkers used proxy exposure variables based on either naïve standardization or on traditional standardization following our proposed pooling strategies.

Results

For all five causal scenarios with urine-based biomarkers, naïve standardization resulted in biased coverage of confidence intervals, whereas covariate-adjusted standardization based on our pooling protocols demonstrated coverage consistent with 95% (Tables 2 and 3). Results for negative coefficients resembled those for positive coefficients (with biases away from the null), so we do not show them. With our pooling protocols, little efficiency was sacrificed until the pooling-set size reached 10. We saw some bias away from the null for the coefficient estimates, but this bias is due to the effective reduction in the sample size from 1000 (K=1) to 100 (K=10), and can be corrected ⁸. The mean width of 95% confidence intervals, proportional to the standard error of estimated regression coefficient, increased with pool size.

Table 2.

Performance comparisons for each causal scenario A, B and B’, for covariate-adjusted standardization using our urine pooling protocols vs. naïve standardization after equal-volume pooling for 1000 simulated studies of 500 cases and 500 controls each.

Beta	Pool size	Naïve Standardization		Covariate-adjusted standardization using our pooling protocols
		95% CI coverage	Bias (SE)	95% CI coverage	Mean 95% CI width	Power	Bias (SE)
			Scenario A
0	1a	0.95	−0.003 (0.003)	0.95	0.42	0.05	−0.003 (0.003)
0	2	0.96	0.000 (0.003)	0.95	0.42	0.05	0.003 (0.004)
0	5	0.95	−0.006 (0.003)	0.96	0.43	0.04	−0.008 (0.004)
0	10	0.95	−0.002 (0.003)	0.95	0.43	0.05	0.006 (0.004)
0.26	1a	0.95	0.003 (0.004)	0.95	0.44	0.97	0.003 (0.004)
0.26	2	0.93	−0.037 (0.003)	0.96	0.44	0.97	0.003 (0.004)
0.26	5	0.92	−0.036 (0.004)	0.95	0.46	0.96	0.008 (0.004)
0.26	10	0.93	−0.029 (0.004)	0.96	0.50	0.97	0.016 (0.004)
0.69	1a	0.95	0.008 (0.004)	0.95	0.50	1.00	0.008 (0.004)
0.69	2	0.81	−0.113 (0.004)	0.95	0.54	1.00	0.013 (0.004)
0.69	5	0.86	−0.102 (0.005)	0.96	0.66	1.00	0.031 (0.005)
0.69	10	0.88	−0.068 (0.007)	0.96	0.92	1.00	0.077 (0.008)
			Scenario B
0	1a	0.95	0.001 (0.004)	0.95	0.44	0.06	0.001 (0.004)
0	2	0.95	−0.008 (0.003)	0.96	0.45	0.04	0.003 (0.004)
0	5	0.95	0.004 (0.004)	0.96	0.49	0.04	0.003 (0.004)
0	10	0.95	0.003 (0.004)	0.95	0.58	0.06	−0.010 (0.005)
0.26	1a	0.95	0.005 (0.004)	0.95	0.45	0.96	0.005 (0.004)
0.26	2	0.93	−0.047 (0.003)	0.95	0.47	0.96	0.005 (0.004)
0.26	5	0.93	−0.028 (0.004)	0.94	0.53	0.91	0.010 (0.005)
0.26	10	0.92	−0.016 (0.005)	0.96	0.65	0.84	0.031 (0.005)
0.69	1a	0.94	0.009 (0.004)	0.94	0.51	1.00	0.009 (0.004)
0.69	2	0.83	−0.123 (0.004)	0.97	0.56	1.00	0.013 (0.004)
0.69	5	0.87	−0.089 (0.006)	0.96	0.74	1.00	0.046 (0.006)
0.69	10	0.92	−0.021 (0.009)	0.96	1.15	1.00	0.118 (0.011)
			Scenario B’
0	1a	0.95	−0.003 (0.003)	0.95	0.42	0.05	−0.003 (0.003)
0	2	0.95	0.000 (0.003)	0.95	0.42	0.05	0.003 (0.003)
0	5	0.95	−0.007 (0.003)	0.95	0.43	0.06	−0.002 (0.004)
0	10	0.95	0.002 (0.003)	0.96	0.43	0.04	0.000 (0.004)
0.26	1a	0.95	0.004 (0.004)	0.95	0.44	0.97	0.004 (0.004)
0.26	2	0.77	−0.110 (0.003)	0.95	0.44	0.97	0.009 (0.004)
0.26	5	0.8	−0.101 (0.003)	0.95	0.46	0.97	0.012 (0.004)
0.26	10	0.81	−0.087 (0.004)	0.95	0.50	0.96	0.017 (0.004)
0.69	1a	0.95	0.001 (0.004)	0.95	0.50	1.00	0.001 (0.004)
0.69	2	0.2	−0.311 (0.003)	0.96	0.54	1.00	0.010 (0.004)
0.69	5	0.39	−0.284 (0.004)	0.96	0.65	1.00	0.011 (0.005)
0.69	10	0.57	−0.256 (0.006)	0.96	0.92	1.00	0.071 (0.008)

^aPool size of 1 means no pooling; analysis used individual observations. In each “pool size 1” row, entries are the same for both naïve standardization and for our proposed methods and are repeated only for convenience.

Table 3.

As for Table 2 except for causal scenarios C and C’, for covariate-adjusted standardization using our serum analyte pooling protocols vs. naïve standardization after equal-volume pooling for 1000 simulated studies of 500 cases and 500 controls each.

Beta	Pool size	Naïve Standardization		Covariate-adjusted standardization using our pooling protocols
		95% CI coverage	Bias (SE)	95% CI coverage	Mean 95% CI width	Power	Bias (SE)
			Scenario C
0	1a	0.96	0.000 (0.003)	0.96	0.43	0.05	0.000 (0.003)
0	2	0.94	−0.002 (0.003)	0.95	0.44	0.05	0.002 (0.004)
0	5	0.94	0.002 (0.004)	0.95	0.49	0.06	0.002 (0.004)
0	10	0.95	0.004 (0.004)	0.96	0.56	0.05	−0.002 (0.005)
0.26	1a	0.95	−0.002 (0.004)	0.95	0.45	0.95	−0.002 (0.004)
0.26	2	0.92	−0.048 (0.003)	0.95	0.47	0.95	0.003 (0.004)
0.26	5	0.93	−0.035 (0.004)	0.96	0.55	0.91	0.016 (0.004)
0.26	10	0.95	−0.016 (0.005)	0.96	0.70	0.79	0.026 (0.006)
0.69	1a	0.96	0.007 (0.004)	0.96	0.52	1.00	0.007 (0.004)
0.69	2	0.80	−0.131 (0.004)	0.96	0.58	1.00	0.021 (0.005)
0.69	5	0.88	−0.093 (0.006)	0.95	0.80	1.00	0.046 (0.007)
0.69	10	0.92	0.007 (0.011)	0.98	1.47	1.00	0.199 (0.014)
			Scenario C’
0	1a	0.95	0.003 (0.003)	0.95	0.42	0.05	0.003 (0.003)
0	2	0.96	−0.003 (0.003)	0.96	0.42	0.04	−0.005 (0.003)
0	5	0.96	−0.004 (0.003)	0.95	0.43	0.06	−0.003 (0.004)
0	10	0.96	0.000 (0.003)	0.95	0.43	0.06	0.008 (0.004)
0.26	1a	0.94	0.001 (0.004)	0.94	0.44	0.97	0.001 (0.004)
0.26	2	0.77	−0.110 (0.003)	0.94	0.44	0.96	−0.003 (0.004)
0.26	5	0.76	−0.110 (0.003)	0.95	0.46	0.97	0.008 (0.004)
0.26	10	0.82	−0.093 (0.003)	0.96	0.50	0.96	0.009 (0.004)
0.69	1a	0.94	0.007 (0.004)	0.94	0.50	1.00	0.007 (0.004)
0.69	2	0.24	−0.306 (0.004)	0.96	0.54	1.00	0.007 (0.004)
0.69	5	0.40	−0.283 (0.004)	0.96	0.66	1.00	0.032 (0.005)
0.69	10	0.57	−0.257 (0.006)	0.96	0.92	1.00	0.077 (0.008)

For all five scenarios with serum-based lipophilic biomarkers, traditional standardization based on our pooling protocols performed well: confidence-interval coverage was near the nominal 95%, bias was generally low, power generally high away from the null, although mean confidence interval length increased with pool size as expected (Tables 4 and 5). Surprisingly, however, naïve standardization provided 95% confidence intervals that exhibited near nominal coverage for scenarios D, E, and E’, though not for scenario F and F’. Generally, logistic models using pools show slight bias away from the null, again reflecting effects of the number of sets in the analysis ⁷. In practice, use of the Firth correction ^8,9, effectively eliminates that small-sample bias (eTable 3).

Table 4.

Performance comparisons for each causal scenario D, E and E’ for lipophilic traditional standardization using our pooling protocols vs. naïve standardization after equal-volume pooling for 1000 simulated case–control studies of 500 cases and 500 controls each.

Beta	Pool size	Naïve standardization		Traditional standardization using our pooling protocols
		95% CI coverage	Bias (SE)	95% CI coverage	Mean 95% CI width	Power	Bias (SE)
			Scenario D
0	1a	0.95	0.003 (0.003)	0.95	0.42	0.05	0.003 (0.003)
0	2	0.95	0.000 (0.003)	0.94	0.42	0.06	−0.006 (0.004)
0	5	0.95	−0.001 (0.003)	0.95	0.43	0.06	−0.002 (0.003)
0	10	0.96	0.000 (0.003)	0.94	0.43	0.06	−0.002 (0.004)
0.26	1a	0.94	0.005 (0.004)	0.94	0.44	0.96	0.005 (0.004)
0.26	2	0.95	−0.012 (0.003)	0.96	0.44	0.98	0.008 (0.004)
0.26	5	0.94	−0.012 (0.004)	0.94	0.47	0.97	0.017 (0.004)
0.26	10	0.94	−0.003 (0.004)	0.97	0.50	0.98	0.017 (0.004)
0.69	1a	0.96	0.002 (0.004)	0.96	0.50	1.00	0.002 (0.004)
0.69	2	0.95	−0.020 (0.004)	0.95	0.54	1.00	0.007 (0.004)
0.69	5	0.94	−0.024 (0.005)	0.95	0.66	1.00	0.013 (0.005)
0.69	10	0.94	0.002 (0.008)	0.97	0.92	1.00	0.067 (0.008)
			Scenario E
0	1a	0.96	−0.003 (0.004)	0.96	0.43	0.04	−0.003 (0.004)
0	2	0.95	−0.002 (0.004)	0.96	0.44	0.04	0.003 (0.003)
0	5	0.95	0 (0.004)	0.97	0.48	0.04	−0.008 (0.004)
0	10	0.96	−0.011 (0.004)	0.95	0.55	0.05	0.005 (0.005)
0.26	1a	0.96	0 (0.004)	0.96	0.45	0.96	0.000 (0.004)
0.26	2	0.96	−0.006 (0.004)	0.95	0.46	0.95	0.002 (0.004)
0.26	5	0.94	−0.009 (0.004)	0.95	0.52	0.93	0.016 (0.004)
0.26	10	0.95	0.002 (0.005)	0.96	0.62	0.87	0.028 (0.005)
0.69	1a	0.94	0.007 (0.004)	0.94	0.51	1.00	0.007 (0.004)
0.69	2	0.95	−0.023 (0.004)	0.95	0.56	1.00	0.009 (0.004)
0.69	5	0.95	−0.005 (0.006)	0.96	0.72	1.00	0.036 (0.006)
0.69	10	0.94	0.073 (0.011)	0.96	1.11	1.00	0.117 (0.010)
			Scenario E’
0	1a	0.95	0.007 (0.003)	0.95	0.42	0.05	0.007 (0.003)
0	2	0.95	−0.003 (0.003)	0.95	0.42	0.05	−0.006 (0.003)
0	5	0.95	−0.001 (0.004)	0.95	0.43	0.05	0.002 (0.003)
0	10	0.96	0.001 (0.003)	0.96	0.43	0.05	0.001 (0.004)
0.26	1a	0.95	0.001 (0.004)	0.95	0.44	0.98	0.001 (0.004)
0.26	2	0.95	−0.008 (0.004)	0.96	0.44	0.97	0.005 (0.004)
0.26	5	0.95	−0.018 (0.004)	0.95	0.47	0.97	0.010 (0.004)
0.26	10	0.95	−0.004 (0.004)	0.95	0.51	0.97	0.023 (0.004)
0.69	1a	0.95	0.008 (0.004)	0.95	0.50	1.00	0.008 (0.004)
0.69	2	0.94	−0.020 (0.004)	0.95	0.54	1.00	0.013 (0.004)
0.69	5	0.94	−0.039 (0.005)	0.95	0.66	1.00	0.014 (0.005)
0.69	10	0.93	−0.005 (0.007)	0.96	0.92	1.00	0.078 (0.008)

^aPool size of 1 means no pooling; analysis used individual observations. In each “pool size 1” row, entries are the same for both naïve standardization and for our proposed methods and are repeated only for convenience.

Table 5.

Performance comparisons for each causal scenario F and F’ for lipophilic traditional standardization using our pooling protocols vs. naïve standardization after equal-volume pooling for 1000 simulated case–control studies of 500 cases and 500 controls each.

Beta	Pool size	Naïve standardization		Traditional standardization using our pooling protocols
		95% CI coverage	Bias (SE)	95% CI coverage	Mean 95% CI width	Power	Bias (SE)
			Scenario F
0	1a	0.94	−0.005 (0.003)	0.94	0.41	0.05	−0.005 (0.003)
0	2	0.94	−0.002 (0.003)	0.93	0.42	0.07	0.002 (0.004)
0	5	0.95	−0.001 (0.003)	0.95	0.46	0.06	−0.002 (0.004)
0	10	0.95	−0.001 (0.004)	0.96	0.52	0.06	−0.005 (0.004)
0.26	1a	0.94	0.003 (0.004)	0.94	0.45	0.96	0.003 (0.004)
0.26	2	0.93	−0.030 (0.004)	0.94	0.47	0.95	0.000 (0.004)
0.26	5	0.92	−0.040 (0.004)	0.96	0.55	0.91	0.023 (0.004)
0.26	10	0.92	−0.027 (0.006)	0.96	0.72	0.78	0.039 (0.006)
0.69	1a	0.95	−0.004 (0.004)	0.95	0.53	1.00	−0.004 (0.004)
0.69	2	0.91	−0.065 (0.005)	0.95	0.61	1.00	0.007 (0.005)
0.69	5	0.89	−0.069 (0.007)	0.95	0.88	1.00	0.045 (0.007)
0.69	10	0.94	0.092 (0.016)	0.98	1.85	1.00	0.228 (0.017)
			Scenario F’
0	1a	0.96	−0.002 (0.003)	0.96	0.33	0.04	−0.002 (0.003)
0	2	0.95	−0.004 (0.003)	0.95	0.33	0.05	−0.002 (0.003)
0	5	0.95	0.006 (0.002)	0.94	0.33	0.06	−0.003 (0.003)
0	10	0.96	0.001 (0.003)	0.96	0.33	0.05	−0.003 (0.003)
0.26	1a	0.96	0.003 (0.003)	0.96	0.35	1.00	0.003 (0.003)
0.26	2	0.93	−0.022 (0.003)	0.95	0.36	1.00	0.004 (0.003)
0.26	5	0.93	−0.031 (0.003)	0.94	0.38	1.00	0.004 (0.003)
0.26	10	0.92	−0.028 (0.003)	0.94	0.43	1.00	0.016 (0.004)
0.69	1a	0.95	−0.004 (0.004)	0.95	0.43	1.00	−0.004 (0.004)
0.69	2	0.91	−0.058 (0.004)	0.96	0.48	1.00	0.004 (0.004)
0.69	5	0.89	−0.074 (0.005)	0.95	0.63	1.00	0.028 (0.005)
0.69	10	0.90	−0.028 (0.008)	0.96	0.99	1.00	0.088 (0.009)

Naïve standardization, because it uses the wrong exposure variable, should show coverage below nominal. Scenarios F and F’ conformed to that expectation, but D, E, and E’ did not. Consequently, we hypothesized that either the bias was quite small or naïve standardization in scenarios D, E, and E’ was producing some counteracting bias toward the null, to yield the correct coverage seen in our simulations. The Firth correction results supported the latter view (eTable 3), as did simulations with a larger sample size. In these simulations, the bias in the naïve standardization for scenarios D, E, and E’ became evident together with the expected below nominal confidence interval coverage (eTable 4). Clearly, nominal coverage cannot be presumed for naïve standardization in scenarios D, E, and E’. Moreover, traditional standardization showed higher power than naïve standardization in these scenarios (eFigure 2).

Discussion

In case–control studies of the effects of environmental factors on risk of disease, high assay costs for exposure biomarkers can limit the affordable sample size. Pooling specimens for assay can make efficient use of the assay budget and of the specimens. Although it can also limit flexibility in considering interactions and transformations during modeling, pooling can substantially enhance power and precision by enabling inclusion of many more cases and controls. Despite these and other advantages ^1,2, a practical problem has discouraged widespread adoption of specimen pooling in environmental epidemiology: one cannot simply adjust a pooled urine sample for dilution by dividing by the creatinine level in the pool, or adjust a pooled serum sample for lipids by dividing by a measure of serum lipids in the pool. Our simulations showed, in fact, that such naïve standardization can distort the estimation of effects compared to individual-based analysis and result in 95% confidence intervals with coverage markedly below 95%.

We proposed two practical strategies that permit creatinine or lipid standardization when pools are assayed: one strategy dilutes each specimen in the pooling set to force them all to have the same concentration of creatinine (or serum lipid); the other selects unequal volumes of the specimens to be pooled. In their simplest forms, these protocols both work because they effectively force the specimens in each pooling set to contribute the same amount of creatinine (for urine) or serum lipid (for serum) to the pool.

Because specific gravity is not as strongly influenced by factors like sex, age, or muscle mass as is creatinine ¹⁰, some studies approach adjustment for differing urine dilutions by instead using specific gravity ^11,12,13. One widely used approach to specific-gravity standardization involves measuring specific gravity in each urine specimen and then forming the standardized exposure $\frac{Z_j}{Q_j}$, where $Q_j=\frac{S{G}_j-1}{S{G}_{{\mathit{REF}}^{-1}}}$. Here SG_j denotes the specific gravity measured in specimen j and SG_REF denotes a selected reference level for specific gravity in the population under study. Our proposed pooling strategies could also be applied to such standardization by replacing C_j with Q_j when calculating dilutions or unequal volumes.

Although this paper has focused on case–control studies, as either retrospective or nested within a cohort, prospective designs with repeated measures also usefully employ specimen pooling ¹⁴. The objectives in a prospective design are usually different; pooling is carried out to reduce extraneous within-person variability from day-to-day fluctuations in analyte levels. The methods we have described can be used for each person, and the regression coefficient based on this pooled predictor should be subject to less bias. A full assessment of the pragmatic need for such methods in a prospective study is, however, beyond our current scope.

For a case–control study, various pros and cons can influence the choice between the two protocols. With the just-add-water protocol, the index creatinine specimen for each pooling set has to be selected to be the most dilute one in that set. The analyte concentration for the pool is thereby forced to be relatively low, which might not be in the optimal range for performance of the assay and might also increase the proportion that fall below the assay’s limit of detection. On the other hand, the just-add-water protocol offers the benefit that once specimens have been appropriately diluted, they will retain their within-pool creatinine level (or serum lipid level) for possible future assessments of other expensive-to-assay analytes. Thus, for each pooling set one should consider formulating a corresponding larger pool to archive for future assays. If instead one uses the unequal-volumes protocol, one can select the index specimen to have a middle-level or higher-level creatinine concentration to help ensure that most concentrations in the constructed pools fall in a better reliability range for the assay. Also, a middle value of the concentration will mean that the volume adjustment factors will be close to one, resulting in volumes contributed by individual specimens that are not too disparate and helping suppress variance attributable to technical measurement errors. Again, one can formulate a corresponding larger pool to archive for future assays. Of course, both approaches require creatinine or serum lipids to be measured beforehand in individual specimens. Another downside to either the just-add-water or the unequal-volumes protocols is that they require additional manipulations (pipetting) and careful attention to what volume is needed from each specimen. With modern automated sample-handling technologies, however, the necessary manipulations should become feasible.

That said, we have not tried out the methods with biospecimens and the pooling process could itself introduce some errors. Even if pooling is done perfectly, Weinberg and Umbach showed that pooling will exacerbate biases caused by assay errors, though it should have no effect on biases due to day-to-day variations. Further consideration of measurement errors would be valuable and is an active area of research ¹⁵, but is beyond our current scope.

In summary, studies using exposure biomarkers as predictors in logistic regression models commonly adjust the measured analyte level in a urine or serum specimen for creatinine or total lipids, respectively. Until now, investigators who wanted to carry out such adjustments could not take advantage of the cost savings and other benefits that accrue from pooling specimens because valid methods for adjustment did not exist. Provided that the creatinine or total lipid levels are measured in advance for individual specimens, our new protocols for pooling specimens enable the desired adjustments and yield valid statistical inference. These methods should encourage wider use of specimen pooling in environmental epidemiology.

Appendix A: The just-add-water protocol.

Here we show that the concentration of primary analyte in a pooled specimen created using the just-add-water protocol is proportional to (and allows straightforward estimation of) the sum of the analyte-creatinine ratios for the individual specimens, which is the exposure measure needed for valid logistic regression based on pooled specimens. The proportionality constant needed is a simple function of the number of specimens and the lowest creatinine concentration in the pooling set.

Suppose a pooling set comprises K specimens, indexed by j ∈ {1, 2, ⋯ , K}, where the individual creatinine concetrations have been measured, and indexed so that j = 1 corresponds to the lowest value. The just-add-water protocol begins by taking a subsample with a common volume, denoted V, from each specimen in the set. Next, this common volume for each specimen in the pooling set is diluted by a factor $\frac{C_j}{C_1}$, so that the volume of specimen j after dilution becomes $V\left(\frac{C_j}{C_1}\right)$. The concentration of analyte in a specimen is defined as the amount of analyte in the specimen divided by its volume; correspondingly, the amount of analyte equals concentration times volume. Thus, the pre-dilution amount of analyte in volume V of specimen j is the product VZ_j and, because the post-dilution concentration, denoted $Z_j^D$, is that same amount divided by the post-dilution volume, we have:

$$Z_j^D=\frac{V{Z}_j{C}_1}{V{C}_j}=Z_j\left(\frac{C_1}{C_j}\right).$$

By a similar argument the creatinine concentrations in the diluted specimens are now all C₁.

After dilution, the protocol specifies taking an equal-volume aliquot from each diluted specimen and pooling them. The measured concentration of primary analyte in the pooled specimen, denoted Z_M, is the average concentration in the component aliquots, i.e., $Z_M=\frac{1}{K}{\sum }_{j=1}^K{Z}_j\left(\frac{C_1}{C_j}\right)$. Consequently, under the unequal-volumes protocol, the sum of the analyte-to-creatinine concentration ratios, the appropriate exposure variable to use in the pool-based logistic model when employing traditional standardization, is given by $\frac{K}{C_1}{Z}_M$.

Appendix B: The unequal-volumes protocol.

The just-add-water protocol described in Appendix A can be seen as a device to ensure that each specimen in the pooling set contributes the same amount of creatinine to the pool. The unequal-volumes protocol achieves that same objective, but through a different approach. We will show that the measured concentration of primary analyte in a pooled specimen created using the unequal-volumes protocol is proportional to (and allows straightforward estimation of) the sum of the analyte-creatinine ratios for the individual specimens contributing to that pool. In addition, the proportionality constant only depends on the creatinine concentrations of the individual specimens.

Suppose a pooling set comprises K specimens, indexed by j ∈ {1,2, ⋯ ,K}, for which the individual creatinine concentrations are assumed to be available to inform the pooling process. A specimen whose creatinine value is near the median for the pooling set is selected to serve as the reference specimen and indexed by j = 1. (Though any specimen could serve, this choice offers practical advantages, as noted in the main text).

The unequal-volumes protocol takes a subsample with volume V_j, from each archived specimen j; these subsamples are combined to form the pooled specimen for assay. First, the volumes needed are calculated so that each specimen will contribute the same amount of creatinine to the pool. Accordingly, the K volumes must satisfy the following relationship for every j:

$$V_j{C}_j=V_1{C}_1$$

or, equivalently,

$$V_j=V_1\left(\frac{C_1}{C_j}\right).$$

The analyte measured concentration in the pooled specimen, denoted Z_M, is the total amount of analyte that the pool contains divided by its volume. The amount of primary analyte in the volume of any individual specimen is Z_jV_j, and thus the total amount in the pool is:

$$\sum _{j=1}^K{Z}_j{V}_j=\sum _{j=1}^K{Z}_j{V}_1\left(\frac{C_1}{C_j}\right)=V_1{C}_1\sum _{j=1}^K\left(\frac{Z_j}{C_j}\right).$$

The total volume of the pooled specimen is:

$$\sum _{j=1}^K{V}_j=\sum _{j=1}^K{V}_1\left(\frac{C_1}{C_j}\right)=V_1{C}_1\sum _{j=1}^K\left(\frac{1}{C_j}\right).$$

The quotient of these two quantities gives the primary analyte concentration in the pool:

$$Z_M=\frac{V_1{C}_1\sum _{j=1}^K\left(\frac{Z_j}{C_j}\right)}{V_1{C}_1\sum _{j=1}^K\left(\frac{1}{C_j}\right)}=\frac{\sum _{j=1}^K\left(\frac{Z_j}{C_j}\right)}{\sum _{j=1}^K\left(\frac{1}{C_j}\right)}.$$

Thus, the primary analyte concentration in the pool is proportional to the sum of the analyte-to-creatinine concentration ratios for the component specimens, and the proportionality constant, ${\left[{\sum }_{j=1}^K\left(\frac{1}{C_j}\right)\right]}^{-1}$, depends only on the creatinine concentrations of the individual specimens.

Consequently, under the unequal-volumes protocol, the sum of the analyte-to-creatinine concentration ratios, the appropriate exposure variable to use in the pool-based logistic model when employing traditional standardization, is assessed as $\left[{\sum }_{j=1}^K\left(\frac{1}{C_j}\right)\right]Z_M$.