Coupled cycling programs multicellular self-organization of neural progenitors

ABSTRACT

Self-organization is central to the morphogenesis of multicellular organisms. However, the molecular platform that coordinates the robust emergence of complex morphological patterns from local interactions between cells remains unresolved. Here we demonstrate that neural self- organization is driven by coupled cycling of progenitor cells. In a coupled cycling mode, intercellular contacts relay extrinsic cues to override the intrinsic cycling rhythm of an individual cell and synchronize the population. The stringency of coupling and hence the synchronicity of the population is programmed by recruitment of a key coupler, β-catenin, into junctional complexes. As such, multicellular self-organization is driven by the same basic mathematical principle that governs synchronized behavior of macro-scale biological systems as diverse as the synchronized chirping of crickets, flashing of fireflies and schooling of fish; that is synchronization by coupling. It is proposed that coupled cycling foreshadows a fundamental adaptive change that facilitated evolution and diversification of multicellular life forms.

Introduction

Self-organization describes the emergence of global order from local interactions between components of a system without supervision by external directing forces. It orchestrates phenomena as diverse as crystal growth, molecular self-assembly, swarm behavior in bacteria and birds and social organization of insects. Self-organization is also central to a major evolutionary adaptation that shaped the biosphere; the advent of multicellularity [1,2]. Unlike unicellular organisms, proper spatial patterning of specialized metazoan cells is critical to the survival of individual cells and the organism. Notably, morphogenic blueprints of complex metazoan organs emerge from simple interactions between cells that possess identical genetic information [2,3]. How such simple interactions instruct optimal spatial positioning and fate specification of progenitor cells remains a mystery. We know, however, that subtle changes in the interpretation of self-organization cues can drive major evolutionary adaptations. Ontogeny of the human brain is an example of altered cellular self-organization; humans benefit remarkably from protracted neurogenesis that improves learning capacity compared to other primates. Insight into the mechanistic basis of neural self-organization would provide a framework to decipher evolutionary adaptations of the human neurosensory apparatus while bypassing the inherent complexity of molecular systems involved in its development.

In principle, the emergence of self-organizing patterns is driven by the exchange of information about the “internal states” of individual components of a system [4]. Subsequent to the exchange of information by local interactions, individuals adopt the internal states of their nearest neighbors which ultimately leads to synchronization of the population and emergence of order [5]. Schooling fish, for example, copy the predominant movement decisions of their nearest neighbors in order to migrate in a synchronized manner [6]. At a micro-scale, neural self-organization is driven by restricted autonomy of individual cells (e.g. during differentiation) via activity of a potential “coupler” that links their “internal states” to that of neighboring cells. This connectivity invokes a form of collective intelligence that guides morphogenesis. Herein we explore the molecular governance of self-organization during human neurogenesis [7] by addressing the following questions: what is the biological correlate of “internal state” in neural self-organization? What is the molecular mechanism for coupling the “internal states” of cells during neural self-organization? Is it possible to control the neural self-organization outcome by modulating the coupling mechanism? We finally combine mathematical and biological self- organization platforms to devise a synthetic programming language that invokes the desired neural self-organization signatures.

We hypothesized that the emergence of self-organization could be controlled by regulation of population-level cell cycle profile. Our findings demonstrate that multicellular self-organization is the outcome of an unexpected evolutionary adaptation; metazoan cell cycle has lost its autonomy in sharp contrast to unicellular organisms that cycle independently.

Materials and methods

Materials and reagents

All chemicals were purchased from Sigma-Aldrich Inc. unless stated otherwise. All primers were purchased from IDT DNA.

Cells

Human brain pericytes, with a demonstrated neural differentiation capacity [7,8], were purchased from ScienCell (Carlsbad, CA). DMEM/F12 supplemented with 10% fetal calf serum, recombinant human FGF-2 20 ng/ml (R&D Systems, 233-FB) and Antibiotic-Antimycotic (100X, Life Technologies) were used for culturing the neural progenitors for analysis of mitotic cycle. To induce neural differentiation, NSCs were cultured in Knockout™ DMEM (Gibco), GlutaMAX™ supplement, N2 supplement (Gibco), and brain-derived neurotrophic factor (BDNF, 10 ng/ml, Sigma).

Immunohistochemistry

Specimens were fixed in 2% paraformaldehyde/5% sucrose in 0.02 M phosphate buffer pH: 7.4 (680 mOsm), for 4 h at 4°C. After blocking in incubation buffer containing 0.1 M PBS, 1% BSA, 0.1% Tween-20, and 5% normal goat serum (for detection with rabbit Abs) or 5% normal rabbit serum (for detection with mouse Abs) for 40 min, sections were incubated with the primary antibodies overnight at 4 °C and secondary antibodies for 1 h at room temperature. Specificity controls were carried out by incubating sections with rabbit or mouse IgG negative control antibodies.

Transmission electron microscopy

For TEM analysis, cells were fixed in Karnovsky’s fixative overnight at room temperature followed by post-fixation in OsO₄ for 1 h. Preparations were dehydrated in graded alcohols and embedded in low viscosity resin (TAAB Laboratory and Microscopy, United Kingdom). Ultrathin sections were mounted on Pioloform/formvar-coated slot grids, stained in uranyl acetate and lead citrate and examined in a Phillips CM120 BioTWIN electron microscope.

Cell cycle analysis by premo™ fucci sensor

Transfection parameters were determined as follows:

Particles per cell: 40

Cell number per dish: ≈ 40,000–50,000

Volume of geminin-GFP or Cdt1-RFP used for each well = 20μl

After adding the reagent based on the calculations above, cells were incubated overnight (16 h) and visualized using a live-imaging microscope (Leica).

Neural organoids

Neural organoids were generated using the hanging drop method. Briefly, the cultured NSCs were gently trypsinized, collected and counted. A minimum of ≈10⁴ cells were re-suspended in 35 μL of the growth medium and loaded onto the cover of an agar plate.

Gene expression analysis

RNA was isolated using the RNeasy Mini Kit (Qiagen). After DNase treatment, reverse transcription of the extracted RNA was carried out using a mixture of 1 μL of oligo-dT, 4 μL of total RNA, 1 μL of dNTP Mix (10 mM each), 4 μL of 5x First-Strand synthesis Buffer, 1 μL of 0.1 M DTT, 1 μL of RNaseOUT (40 units/μL), 1 μL of SuperScript-III reverse transcriptase (200 units). Reverse transcription was performed at 50°C for 50 min followed by 55°C for 15 min. RNA was subsequently digested with RNAase H. To design primers, gene sequence data and exon/intron boundaries were obtained from the GenBank database (see supplementary Table S1). In each of the primer sets, the common 3΄ or 5΄ primer spanned the adjacent exons to prevent amplification of genomic DNA.

Real-time PCR

Real-time PCR (38 cycles) was performed using SensiFAST™ SYBR® Lo-ROX reagents (BIOLINE®). Reaction mix comprised of 2 μl of cDNA, 400 nM inner primers (1.5 μl/primer), 10 μl of 2x SensiFAST SYBR Lo-ROX Mix, and 5 μl of PCR-grade water on a Stratagene® Mx3000P real-time PCR instrument. The average efficiency of PCR amplification for each gene of interest was quantified based on a linear regression model using the LineRegPCR software. The relative expression ratio of the gene of interest (test:control) was then calculated using the efficiency (Eff.) values based on the method proposed by Pffafi as follows:

$$Ratio=\frac{{(Ef{f}_{tar})}^{\mathrm{\Delta }c{t}_{tar}(control-test)}}{{(Ef{f}_{ref})}^{\mathrm{\Delta }c{t}_{ref}(control-test)}}$$

Small molecule inhibitors

BIO (GSK3β inhibitor, catalog no. B1686), IWR-1 (axin-1 stabilizer, catalog no. I0161), and ML141 (CDC42 inhibitor, catalog no. SML0407) were all purchased from Sigma-Aldrich. The inhibitors were applied at a final concentration of 1 μM for 24 h.

Live-imaging analyses

For live-imaging analysis cells were cultured in six-well plates overnight and transferred into the live-imaging platform (Leica DMI6000B live cell imaging microscope). Phase contrast images were captured every 4 min for 36 h from multiple wells (10x magnification). To analyze mitotic activity, images were imported into FIJI (ImageJ) platform and cell divisions (m_i: mitosis) were binned in 40-min periods (t_i: periods) with M-phase defined as cell rounding until the end of cytokinesis. The cumulative division graphs (continuous lines of Figure 2(b)) for the data points (t_i, m_i) were generated as follows:

$$\begin{array}{rl}& i=\{1,\dots ,50\}\\ & t_i=i\times 40\\ & m_i=\sum _{t_i=1}^{2000}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{t}{\mathrm{s}}_{{\mathrm{t}}_{\mathrm{i}}}\end{array}$$

Figure 2.

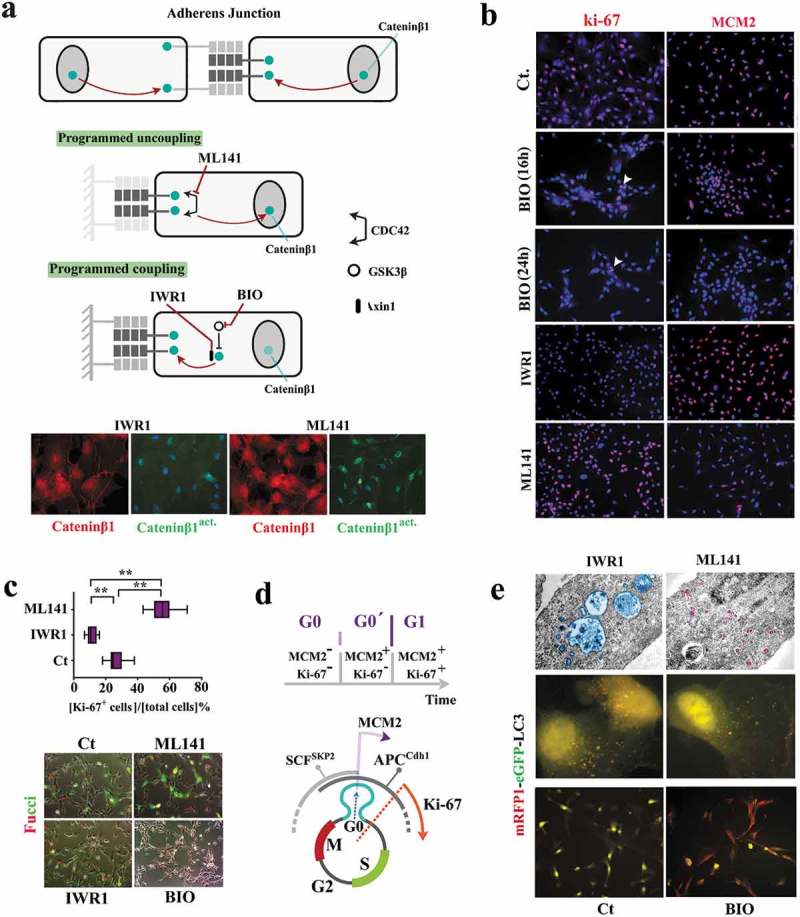
Reprogramming of coupled cycling using small molecule inhibitors.

(a) Schematic image shows the molecular basis for modulating subcellular localization of β-catenin in order to program coupled cycling. Note that the application of a coupling enhancer (IWR1) triggers the depletion of active nuclear catenin-β1 (catenin-β1^act.) by recruitment into the junctional complexes. Application of a coupling suppressor (ML141) induces the opposite signature (scale bar: 20μm). (b) Ki-67 and MCM2 report the synchronization state of neural progenitors subsequent to the application of coupling enhancers (BIO and IWR1) and a coupling repressor (ML141) (scale bar: 60μm). (c) Ki-67 immuno-reactivity (n = 15 fields) suggests Synchronization of uncoupled cells (ML141⁺) at late G1 as opposed to G0 Synchronization coupled IWR1⁺ cells. Fucci reporter dye confirmed the proposed state of cycle subsequent to the application of inhibitors (scale bar: 35μm). ** indicates p < 0.01. (d) Schematic demonstration of molecular signature that characterizes G0 (early G0), G0ˊ (late G0), and G1. (e)Electron micrographs demonstrate autophagosome formation (blue) in IWR-1⁺ cells. Note the enhanced endocytosis (purple granules) in ML141⁺ cells due to destabilized junctional complexes subsequent to the inhibition of CDC42. Analysis of autophagic flux by RFP/GFP‐tagged LC3 reporter plasmid, ptfLC3, confirmed ultrastructural findings (top scale bar: 0.4 μm, middle scale bar: 5μm, bottom scale bar: 45μm). Note that autophagic flux in simulated coupling (IWR⁺, BIO⁺) increases. In Bio⁺ cells autophagy is highly active (RFP⁺/GFP⁻).

The cumulative linear mitotic rate (Lmr) defined the slope (α) of the least-squares regression line where m and t correspond to the data points (t_i, m_i). The second parameter measures deviation (dm_i) of the observed mitotic events (t_i, m_i) from those predicted by the linear regression model

$$\begin{array}{rl}& \mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}=\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}\mathrm{m}-\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{m}\\ & \mathrm{d}{\mathrm{m}}_{\mathrm{i}}=\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}{\mathrm{m}}_{\mathrm{i}}-\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}{\mathrm{m}}_{\mathrm{i}}\end{array}$$

Data were imported into MATLAB to build the regression model and calculate mitotic residuals using the curve fitting app of MATLAB.

The locomotory landscape was constructed by measuring the average velocity of cells (V_av) in a field of view:

$$v_{av}=\frac{\sum _{j=1}^N\sum _{i=1}^{30}{v}_i^j}{N}$$

where N represents the number of mobile cells tracked and binned in 60-min intervals (i = 30 frames).

Mathematical modeling of synchronized cycling

We simulated the cycling cells as a population of N coupled phase oscillators based on the Kuramoto model and using MATLAB. Cell cycle was modeled as an abstract limit cycle and ${\theta }_k$ (phase variable) that describes progress through the cell cycle of a progenitor cell (k) with reference to the forthcoming mitosis that resets the phase variable to zero (Supplementary Fig. S3). In the model, natural (uncoupled) cycling frequencies (ω_k) of proliferating cells are synchronized to other members of the population by a coupling mechanism:

$$\frac{d{\theta }_k}{dt}={\omega }_k+\sum _{z=1}^N{K}_{kz}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_z-{\theta }_k\right)$$

where K is the coupling strength, and N is the number of cycling cells.

Statistical analysis

SPSS statistical software (SPSS v.16, Chicago, Illinois, US) was used for the statistical analysis of data. The relative expression levels of genes of interest were compared using univariate ANOVA and non-parametric Mann-Whitney U test. In the present study, a p-value<0.01 was considered as statistically significant.

Results

Individual neural progenitors copy the cell cycle state of neighboring cells

As a pre-requisite for self-organization, we began by exploring the biological basis for an “internal state” that restricts the autonomy of individual cells by adapting to the internal states of other cells in a population. Cell cycle orchestrates fundamental decisions such as cell fate specification [9] and spatial navigation [10]. We investigated whether cell cycle, as a proxy for the “internal state”, is entirely autonomous or adapts to the cell cycle of neighboring cells. We used 2D cultures of neural progenitor cells [7,8] that migrate at an average velocity of 20nm/sec. In a 2D culture system, human neural progenitors (HNPs) organize into synchronously cycling clusters (Figure 1(a)). High-resolution single cell tracking of cycling HNPs that express the Fucci reporter dye revealed an unexpected mode of synchronization. Individual cells, upon encountering a cluster of G1 phase cells, abort their intrinsic cycle state and adopt the dominant cycle state by regression from G2 to G1 phase of the cycle (Figure 1(a-c) Supplementary Movies S1, S2). Directionality of the cell cycle is mainly attributed to a temporally programmed proteolysis and experimental modulation of cyclin profile triggers a reversal from G1 to M phase of cell cycle [11]. Our findings provide additional evidence for inherent contact-dependent reversibility of cell cycle from G2 to G1 phase. A similar mechanism drives developmental endocyling where a reversal of cell cycle from G2 to G1 phase is required in order to re-enter S phase [12]. As such, we anticipated improved synchronization of the cycling cells in a 3D milieu due to the enhanced stability of intercellular communications.

Figure 1.

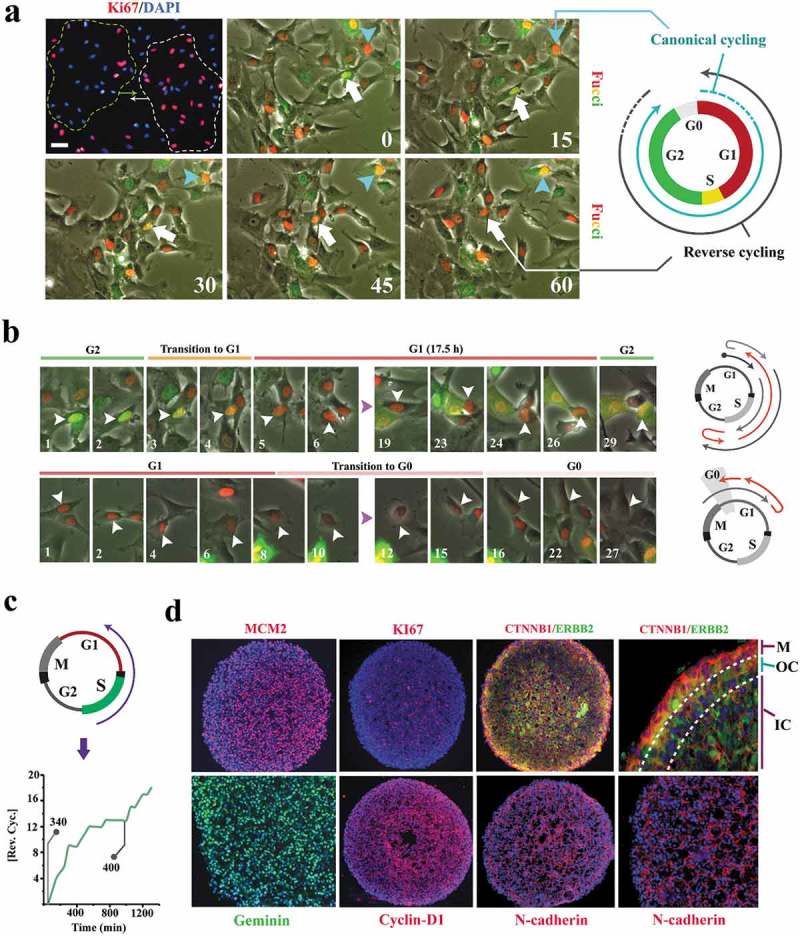
Cell cycle state of individual neural progenitors is programmed by other cells in the population.

(a) Synchronized clusters of migratory Ki-67⁺ and Ki67⁻ cells (top left, dotted lines) can either form by random localization of cells that are in the same phase of cycle or by de novo synchronization subsequent to clustering (top left scale bar: 40μm, top middle scale bar: 20μm). Live- imaging analysis by application of Fucci reporter dye shows de novo synchronization by reversal of the cell cycle directionality of an individual cell (white arrow) in order to adapt to a cluster of G1-Synchronized cells (red nuclei). In the absence of clustering, cell cycle progresses in the expected direction (turquoise arrow). Timestamps are in minutes. (b)Synchronized clusters convene at G1 by two parallel mechanisms. Cells that are in G2 regress to G1 and cells that are at G1 dwell longer in this phase by regression to G0 (timestamp unit = 50 min; scale bar: 10μm). (c) Line graph shows the cumulative incidence of reverse cycling detected by Fucci reporter dye. The two grey lines indicate the total number of cells at t = 0 (n = 340 cells) and t = 1000 min (n = 400 cells). (d) The majority of the organoid cells synchronize to early G1 within 16 h. Note the depletion of cytoplasmic β-catenin (CTNNB1), a major driver of the cell cycle, by recruitment into intercellular junctions (N-cadherin). In the outermost layer, where intercellular contacts are diminished, β-catenin becomes detectable in the cytoplasm. ERBB2 (Her2) is a major inhibitor of GSK3β and hence rescues β-catenin that is subsequently recruited to junctional complexes (top left scale bar: 120μm, top right scale bar: 40μm, bottom scale bars: 60μm). M: Mantle layer; OC: outer core cells; IN: inner core cells.

To test this hypothesis, we generated neural organoids. Within 16 h of organoid formation, the majority of progenitor cells were identified as MCM2⁺/Ki67⁻ (Figure 1(d)). A small number of cells were identified as MCM2⁻/Ki67⁻ (Figure 1(d)). MCM2 (Minichromosome Maintenance Complex Component 2) is a component of the pre-replication complex assembled in early G1 [13] and Ki67 is expressed upon progression into late G1 [14]. The MCM2⁺/Ki67⁻ profile is therefore consistent with near-complete synchronization of organoid cells at G0 (defined by Ki67⁻ profile) with a commitment (MCM2⁺) to progress into S phase (Figure 1(d)). Due to such commitment (MCM2⁺), we termed the MCM2⁺/Ki67⁻ phase as late G0 (that is termed G0ˊ in this paper). On the other hand, the MCM2⁻/Ki67⁻ profile is consistent with synchronization at early G0 (non-committed G0 that implies a lack of commitment to progress into G1). In a control 2D culture, only ≈50% of progenitor cells completed the mitotic cycle within 16 h (supplementary Fig. S1). Given the longer timespan required for progression of all cells into G0 by completion of a mitotic cycle (≈50% of cells in 2D versus 100% in 3D), we concluded that synchronization of cells within an organoid should mainly occur by regression into early and late G0 analogous to the observed synchronization of cycling cells in 2D (Figure 2(b,c)). Expression of Geminin (inhibitor of DNA replication that is confined to S and G2 phases) and cyclin-D1 provided further evidence that synchronization has occurred by regression into G0 (as opposed to completion of mitosis) subsequent to the formation of an organoid (Figure 1(d)). These observations suggest a fundamental adaptation of the metazoan cell cycle, that is, coupling to other cycling cells. By restricting the autonomy of individual cycling cells and installing a collective behavior, the coupling could facilitate emergence of order during morphogenic self-organization. We next investigated the molecular basis for coupled cycling of progenitor cells.

Subcellular localization of β-catenin programs synchronized cycling of individual cells

In a simplified model, coupled cycling can occur if a major driver of the cell cycle is regulated by intercellular contacts. β-catenin fulfills such a requirement. The transcriptional activity of free cytoplasmic β-catenin in driving cell cycle [15] is counterbalanced by recruitment of this protein into cadherin-based intercellular junctions [16] (Supplementary Fig. S2). To probe the putative coupling activity of β-catenin, we used several small molecule inhibitors (Figure 2a). A Gsk-3β inhibitor, BIO [17], was employed (1μM) to restrict the degradation of cytoplasmic β-catenin [18] and enrich the fraction bound to junctional complexes. Likewise, an Axin-1 stabilizer (IWR-1, 1μM, 24 h) was used to enhance the stability of this protein and recruit the cytoplasmic β-catenin, in association with Axin-1, into cadherin-based junctions [19]. Conversely, we used a CDC42 inhibitor, ML-141 [20] (1μM, 24 h), to destabilize cadherin-based junctions [21] and release the sequestered β-catenin. Subsequent to the application of BIO, progenitor cells became MCM2⁻/ki67⁻ (Figure 2(b)). This profile is consistent with synchronization at early G0 (non-committed G0 prior to assembly of the pre-replication complex). Likewise, enrichment of junctional β-catenin by the application of IWR-1 synchronized ≈90% of progenitor cells into late G0 (ki67⁻/MCM2⁺ phase) (Figure 2(b-d)). Contrarily, the enrichment of cytoplasmic catenin-β1 (by applying ML-141) coerced a ki67⁺/MCM2⁻ profile in ≈60% cycling neural progenitors suggesting an aborted early G1 synchronization followed by accelerated progression into interphase (Figure 2(b-d)). We noted that the induction of an autophagic flux was required to regress from G0ˊ into G0 (Figure 2(e)). This is because further depletion of β-catenin by autophagy [22] complements reduction of the cytoplasmic pool of the protein by recruitment to junctional complexes. The data suggest that β-catenin acts as a binary switch for programming the coupling stringency and synchronicity of a cycling population. Free cytoplasmic β-catenin signals the uncoupled state or a paucity of neighboring cells and drives the progression of cell cycle. On the other hand, recruitment of β-catenin to junctional complexes signals the coupled state or the availability of neighboring cells with a resultant delay at G0/G0ˊ. Such transient delay improves synchronicity of the population. To complement the cross-sectional measurements and access the temporal landscape of synchronicity of the population, a reporter-independent method of tracking cell cycle by live imaging was required. This is because reporter-dependent measurements at a temporal resolution are associated with phototoxicity, DNA damage and altered kinetics of cell cycle.

The proposed model for the emergence of synchronization reflects a fundamental property of many other oscillatory systems where coupling (i.e. transfer of information between individual components) occurs. Examples include synchronized oscillations of coupled pendulums and activity of pacemaker cells in the heart. In these systems, emergence of synchronization can be accurately described by a simple mathematical platform, the Kuramoto model [23]. We, therefore, measured the synchronicity of cell division by phase contrast live imaging (see methods) and utilized the Kuramoto model to extrapolate the synchronicity of cell cycle.

Kuramoto model accurately predicts coupling dynamics of the cycling neural progenitors

In the basic version of the Kuramoto model, intrinsic frequency of individual oscillators synchronizes to that of the others by a coupler that accelerates the slower oscillators and decelerates the faster ones [23,24]. Using the Kuramoto model, we simulated the synchronized mitotic entry of progenitor cells, as an index (or an outcome) of synchronized cycling. The equivalent in vitro index was generated by tracking the synchronicity (±20 min) of cell divisions (see methods and supplementary Fig. S3). Synchronized divisions lead to mitosis-rich periods that are followed by mitosis-poor temporal windows. The resultant temporal oscillation of the cumulative incidence of cell divisions was measured by regression of a straight line onto the data. The amplitude of oscillations (mitotic residuals in Figure 3) reflects the synchronicity and hence the coupling stringency of cycling cells. Upon calibrating parameters of the Kuramoto model (Supplementary Fig. S4), we noted that a weak coupler (Coupling constant = 0.00005) can accurately simulate the in vitro synchronization signature of proliferating cells (Figure 3(a,b), Supplementary Fig. S5). In agreement with findings in vitro (Figure 1(a,b)), modeling indicated that deceleration of the fast oscillators (abstraction of the regression of cell cycle presented in Figure 1) was central to the emergence of the synchronization signature (Figure 3(a)). We then investigated the numerical predictability of coupling and uncoupling dynamics. At this stage, small molecule inhibitors were applied at a lower dose (100 nM) to avoid full synchronization/desynchronization of cells. Enhanced coupling stringency (IWR1⁺ cells) delayed mitotic entry of the fast cycling cells by amplifying G0/early G1 synchronization (Figure 3(c)). Contrarily, uncoupling of the cycling cells (ML141⁺ cells) restored the intrinsic rhythm of fast cycling cells (by removal of the extrinsic decelerating cues ofcell cycle) and propelled precocious entry into mitosis by these cells (Figure 3(c)). Programming of Kuramoto oscillators accurately simulated the coupling and uncoupling dynamics of the population. The simulations confirmed numerical programmability of the coupling stringency of cycling cells, to regulate the length of G0/early G1 and the synchronicity of a cycling population, by manipulation of subcellular localization of β-catenin (Figure 4(a)). Remaining unanswered is whether the numerical predictability of the coupling dynamics translates into the predictability of fate specification and spatial organization.

Figure 3.

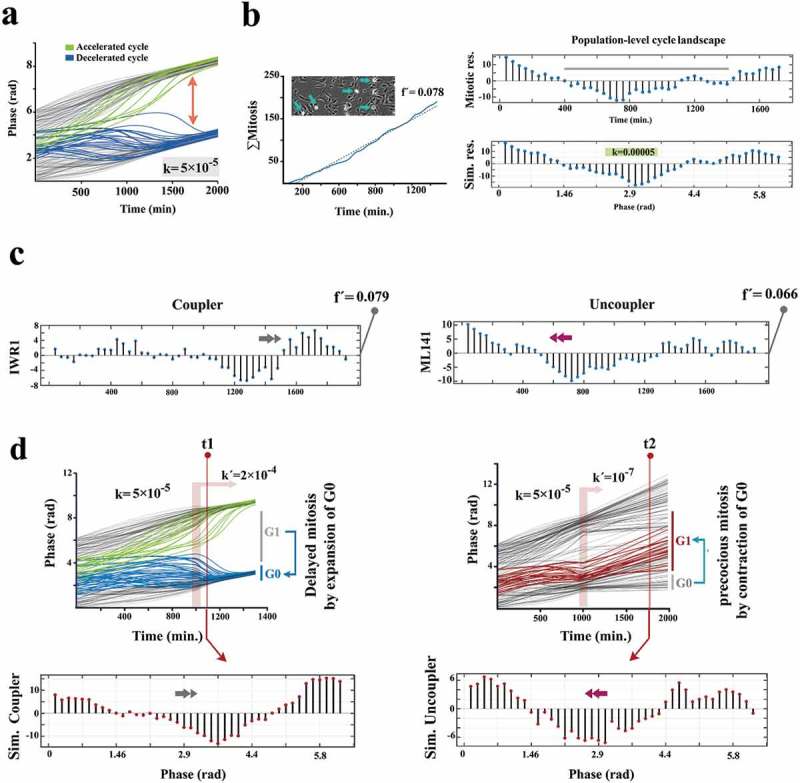
Kuramoto model accurately predicts coupling dynamics of the cycling neural progenitors.

(a) Simulated emergence of synchronized cell divisions under instruction from a weak coupler. Phase angle (y-axis) represents the progress of progenitor cells (n =150 cells) through an abstract cell cycle with reference to the forthcoming mitosis that occurs at phase angle = 2Π (see methods for details). As such, the coupler instructs emergence of complete phase locking (full synchronization) at t = 1300 min. from the random distribution of phase angles (uncoupled/non- synchronized state) at t = 0. In this timeframe, the partial synchronization that occurs at t = 700 is compatible with the in vitro synchronization signature of progenitor cells. (b)The left panel shows the cumulative incidence of cell division (blue line) and the associated regression line (dotted grey line, fˊ = slope of the regression line). Phase contrast image shows an example of synchronized divisions (blue arrows) that generate positive deviations of mitotic incidence from linearity. Such deviations from linearity of cell division (mitotic residuals: mitotic res.) are in vitro signatures of coupled cycling (top right). The in vitro signature is accurately simulated by Kuramoto model of synchronization (bottom right, t = 700 as explained in part a). (c) Representative temporal signatures of mitotic synchronicity subsequent to increased (IWR1) and decreased (ML141) stringency of coupling were developed by application of inhibitors at a concentration of 100 nM (see methods). (d) Simulated emergence of synchronicity after increased (top left) and decreased (top right) coupling stringency that occurs at t = 1000 min (pink ribbon, kˊ indicates the altered coupling constant). The synchronicity profiles compatible with the in vitro signatures were observed at t1 (100 min. after the enhanced coupling) and t2 (750 min. after uncoupling). Biological interpretations of the simulated profiles of synchronicity are found next to the emergence plots.

Figure 4.

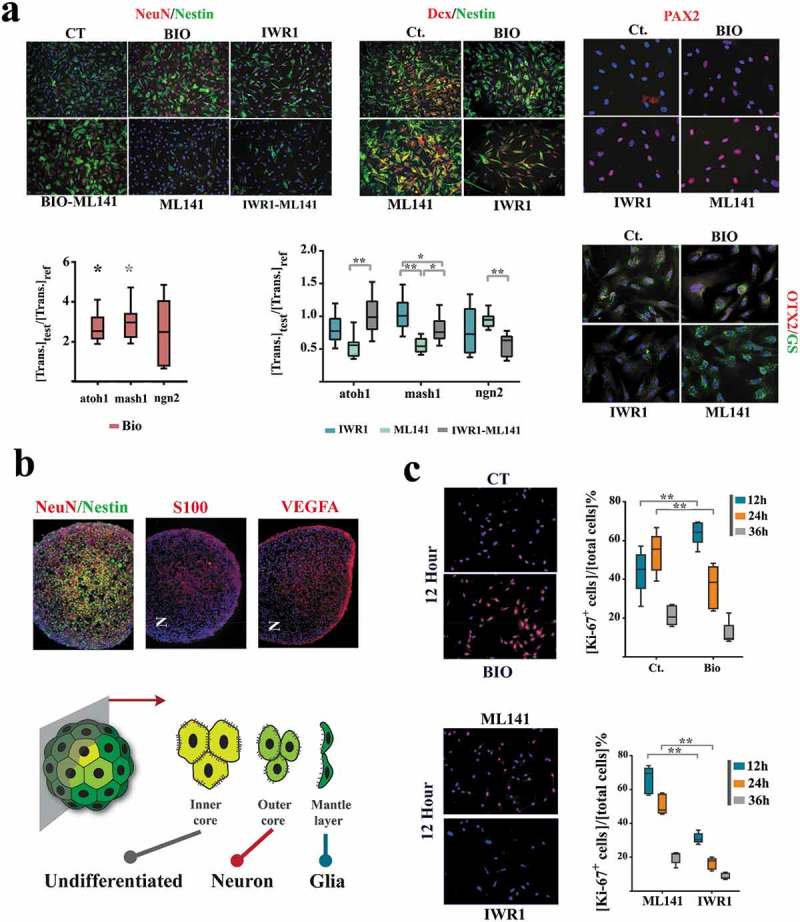
Sub-lineage fate specification of neural progenitors is programmed by coupling dynamics of the population.

(a) ML141⁺ neural progenitors demonstrate a glial differentiation bias (NeuN⁻, Nestin⁻, Glutamine synthase⁺ (GS⁺), top). IWR1⁺ cells demonstrate neuronal differentiation bias that is offset by simultaneous application of ML141. BIO⁺ cells (synchronized at G0) remain quiescent (Nestin⁺, Dcx⁻, atoh1^high, mash1^high) subsequent to the induction of differentiation and this state is not counterbalanced by simultaneous application of ML-141 (top left scale bar: 55μm, top middle scale bar: 45μm, top right scale bar: 20μm). The expression level of genes of interest are normalized β-actin and referenced to the control group (n = 3 biological replicates). * indicates p < 0.05 and ** indicates p < 0.01. (b) In neural organoids, inner core cells are mainly Nestin⁺. The cells in the outer core are NeuN⁺ and those in the mantle layer are S100⁺/VEGF⁺ (scale bar: 120μm). Note the radial polarity of NeuN⁺ cells as opposed to the the axial polarity of S100⁺/VEGF⁺ pro-glial cells. (c) Expression of Ki-67 in various treatment groups (n = 15 fields) after the induction of differentiation (scale bar: 55μm). ** indicates p < 0.01.

Coupled cycling of cells communicates biased sub-lineage fate specification

We initially investigated the impact of coupling stringency on sub-lineage differentiation outcome of neural progenitors upon differentiation. Cells were programmed by the application of small molecule inhibitors for 24 h in growth medium. To initiate neural induction, the inhibitors were washed out and the programmed cells were incubated in neural induction medium for 24 h. We noted that enhanced coupling stringency (IWR1⁺ cells, synchronized at G0ˊ) instructs a neuronal differentiation bias as opposed to glial differentiation of the uncoupled ML141⁺ cells (Figure 4(a)). Cells synchronized at early G0 remained resistant to differentiation cues for 24 h (Figure 4(a)). We compared this signature to that of neural organoids. In neural organoids, peripheral cells (mantle layer, characterized by high cytoplasmic β-catenin analogous to ML141⁺ cells) showed a glial differentiation bias (Figure 4(b)). Pro-glial cells also demonstrated significant axial polarity (dominance at one pole). Conversely, cells in the outer core of the organoid (β-catenin^low analogous to IWR⁺ cells) demonstrated a neuronal differentiation bias (Figure 4(b)). Cells in the inner core of the organoid (β-catenin⁻/ERBB2⁺ analogous to BIO⁺ cells) remained NeuN⁻/Nestin⁺, consistent with resistance to differentiation (Figure 4(b)).

In order to disclose the temporal emergence of various fate outcomes, we profiled Ki-67 expression at 12, 24, and 36 h after the induction of differentiation (Figure 4(c)). As expected, IWR⁺ cells differentiated faster due to synchronization at pro- differentiation late G0 (G0´). Differentiation of ML141+ cells was delayed for 24 h due to synchronization at late interphase that demanded completion of another mitotic round prior to entry into G1 (Figure 4c). This temporal signature is consistent with earlier emergence of neuronal fate during development [25]. Findings are aligned to the demonstrated role of β-catenin in instructing a neuronal fate outcome [26]. While enrichment of cadherin-bound β-catenin manifests as improved synchronicity of cycling progenitor cells, release of this protein from junctional complexes, upon a commitment to differentiation [27], enforces a neuronal differentiation bias (Figure 4b). On the other hand, differentiation of BIO⁺ cells was delayed for 12 h (evidenced by retention of ki-67 expression) due to synchronization at early G0 (quiescence). Synchronization at G0 with high autophagic flux maintains stemness [28] in part by degrading the β-catenin that is released from junctional complexes during differentiation. We eventually asked if the demonstrated differentiation bias is also linked to a spatial organization bias.

Coupled cycling of cells programs spatial self-organization of organoids

Cellular navigation is in part regulated by combined activities of attractive intercellular cues such as cdh-2 [29] and repulsive intercellular cues such as slit-1 [30]. As intercellular cues synchronize cycling cells to G0/G0ˊ, it was not surprising to detect downregulation of these cues in parallel to progression into late G1 (Figure 5(a), Supplementary Figs. S6, S7). The intercellular cues were upregulated in G0ˊ compared to G0 (Figure 5a,b). Following this observation, we combined progenitor cells pre-conditioned with BIO (synchronized at G0), IWR1 (synchronized at early G1) and ML141 (synchronized at G2 phase) for 16 h. The organoids formed by a random mixture of BIO⁺ and IWR1⁺ cells (1:1 ratio) exhibited remarkable radial polarity characterized by an inner core of BIO⁺ and an outer layer of IWR1⁺ cells (Figure 5(c)). This signature is consistent with endogenous self-organization of neural progenitors where neuronal fate dominated the outer core and the undifferentiated Nestin⁺ cells occupy the inner core of organoid (Figure 4(b)). On the other hand, the organoids formed by a random mixture of BIO⁺ and ML141⁺ cells (1:1 ratio) demonstrated axial polarity with BIO⁺ cells pooled in one pole and the ML141⁺ cells in the opposite pole (Figure 5(d)). This signature simulates the polarized enrichment of glial cells in the mantle layer of the organoid (Figure 4(b)). These observations foreshadow the alignment of numerical predictability of coupling dynamics (based on Kuramoto model) to the predictability of fate and spatial self-organization. We concluded that multi-cellular self-organization memory could be accurately programmed by the stringency of coupled synchronization of cycling cells.

Figure 5.

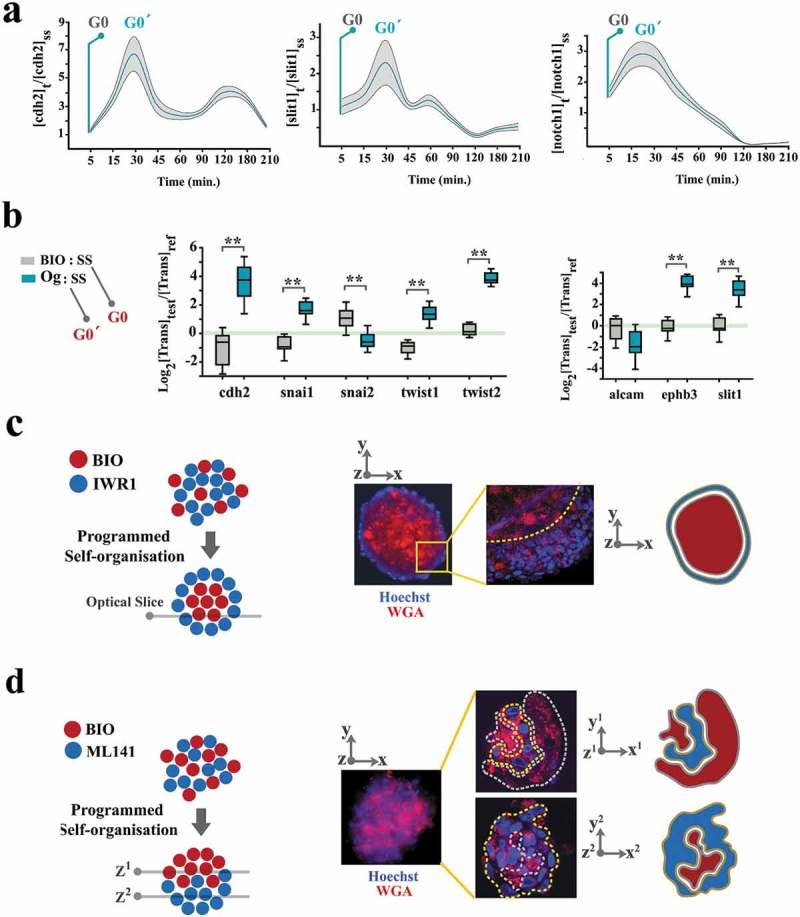
Spatial self-organization of organoids is programmed by coupling dynamics of the population.

(a) To uncover cell cycle-mediated modulation of intercellular communication cues, cells were initially synchronized at G0 by serum starvation and forced into G1 by adding serum. Graphs demonstrate the levels of gene expression normalized to t₀ (serum starvation) (n = 3 biological replicates). Turquoise line: mean value, grey ribbon: ±SEM. (b) Box plots demonstrate the levels of expression genes that regulate intercellular communication cues in neural organoids (Og) and BIO+ cells, both normalized to cells in a serum-starved mode (SS) for 24 h. Note that organoid cells (synchronized at G0ˊ) express a higher level of these transcripts analogous to t = 30 min in part a when cells progress into G0ˊ from G0 by addition of serum to the starved cells. (c)A representative organoid shows the radial organization of BIO⁺ and IWR1⁺ cells. Wheat germ agglutinin-Alexa594 was used to label BIO-treated cells and Hoechst labeled the cells treated with IWR1 (top left scale bar: 100μm, top right scale bar: 25μm). High magnification image (right image) shows an optical slice of the organoid captured using confocal microscopy. (d)A representative organoid shows the polarised organization of BIO⁺ and ML141⁺ cells. Wheat germ agglutinin- Alexa594 was used to label BIO- treated cells and Hoechst labeled the cells treated with ML141 (top left scale bar: 100μm, top right scale bar: 50μm). High magnification image (right image) shows two optical slices of the organoid (1: top, 2: bottom of the organoid) captured using confocal microscopy.

Discussion

Data presented herein provide evidence regarding coupled cycling of human neural progenitor cells. In a coupled cycling mode, intercellular contacts reprogram the intrinsic cycling rhythm of individual cells and improve synchronicity of the cycling population (Figure 6(a)). Recruitment of β-catenin into junctional complexes synchronized the cycling cells and mobilization into the cytoplasm has the opposite effect of de-synchronization. While coupled cells assume a neuronal fate bias upon differentiation, uncoupled cells mainly differentiate into glial cells. The fate bias is combined with a spatial organization bias. During self-organization morphogenic signatures emerge as the fate and spatial biases associated with an individual cell are linked to those of the other cells due to coupled cycling. It is the strength of coupling that determines the outcome of morphogenesis.

Figure 6.

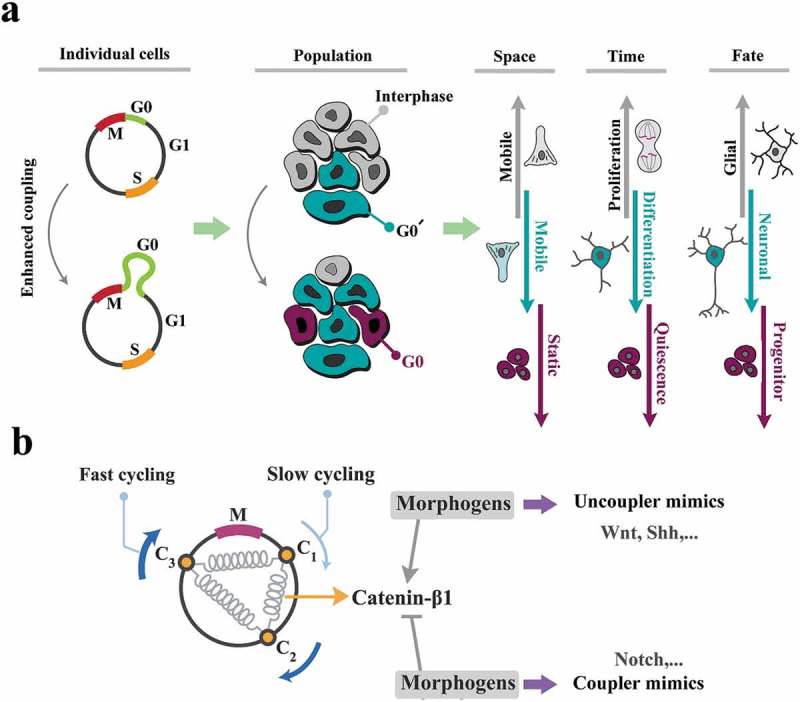
The cell cycle is key to the self-organization of neural progenitors.

(a) Enhanced coupling stringency leads to amplification of G0/G0ˊ phases of cell cycle and subsequent- synchronized progression into interphase at a population level. The very same siganture, at an individual cell level, instructs spatial navigation, proliferation, and fate specification biases. As such, increased coupling stringency improves synchronicity of the cycling cells by decelerating the cell cycle and in parallel, delays differentiation. Upon differentiation, the same mechanism induces neuronal fate bias. Uncoupling instructs the opposite phenotype. (b) Morphogenes may be interpreted as the enhancers or the suppressors of coupling strength (schematized as springs) in order to synchronize/desynchronize the population and invoke the morphogenic signatures.

Global synchronization of the cell cycle has been described in various unicellular organisms. For example, unicellular eukaryotic amoebae Dictyostelium discoideum switch to a synchronized cycling mode upon starvation in order to form the multicellular slime mold [31]. Such synchronised cycling has been attributed an unknown diffusible factor [31]. We propose that contact-dependent coupled cycling was a major evolutionary step in the adaptation to multicellularity by programming self-organization memory and collective behavior of cells during morphogenesis. β-catenin was pivotal in orchestrating coupled cycling of the eukaryotic cell cycle. Notably, free cytoplasmic β-catenin is rapidly degraded [32]. It is therefore expected that the half-life of free cytoplasmic β-catenin would determine the coupling strength of cycling cells with resultant alteration of the downstream morphogenic signatures. The proposed mechanism of enhanced coupling stringency could explain why stabilization of β-catenin during brain development amplifies cerebral cortical gyrification [33]. On the other hand, the abnormal cortical development in Miller-Dieker Syndrome that manifests as the opposite phenotype of reduced gyrification (lissencephaly) is linked to the disruption of N-cadherin/β-catenin axis [34]. From this perspective, the morphogenic capacity of major developmental signaling pathways, such as Wnt cascade, could have been a consequence of co-opting the basic coupling activity of β-catenin (Figure 6(b)). If this hypothesis is true, one would expect evidence for independent signaling activities of Wnt and β-catenin. Interestingly, emerging evidence suggests that Wnt-independent signaling by β-catenin [35] and β-catenin-independent signaling by Wnt [36] complement the activity of the canonical Wnt/β-catenin axis. Further evidence is required to confirm the proposed interpretation of the action of morphogens.

From a mathematical perspective, the proposed mechanism of self- organization provides a biological foundation for the long-established reaction-diffusion mechanism of morphogenesis [37]. The mathematician, Alan Turing (1952), proposed a theoretical model for morphogenesis [38] that inspired many others to build upon and expand the field. Despite the remarkable success of reaction-diffusion models in predicting morphogenic outcomes, the application to real-world problems has been surprisingly limited. This in part due to the lack of a credible biological basis for idealized theoretical parameters that coordinate self-organizing systems; a “coupler” that can be experimentally programmed to induce self-organization and the subsequent “symmetry breaking” that creates morphogenic patterns. The proposed paradigm for self-organization links the reaction-diffusion model and biological platforms for the first time and enables the translation of a rich mathematical background into biological outcomes.

The proposed unifying model of morphogenesis provides direct low-level (i.e. downstream) insight into currently inaccessible phenomena such as adaptations characteristic of the human brain. While complex systems-level interactions would remain a challenge to decipher, the morphogenic signature communicated by these cascades can now be analyzed based on coupling dynamics. Further, interpretation of altered self-organization language in dysmorphogenesis, e.g. developmental syndromes, will be facilitated by the adoption of the model. The simplicity of the proposed self-organizing platform has therapeutic implications. Analysis of the altered self-organization signature (based on the methodology provided) could inform the design of novel therapeutics that target and correct the coupling dynamics without identifying the systems-level deficiencies that may be complex to dissect and costly to remediate. This is akin to mechanisms that induce robustness during development; perturbations of a signaling cascade are compensated by hyperactivation in parallel of another signaling cascade [37].

In conclusion, we envisage that the proposed model will provide a novel approach to reinterpret complex morphogenic phenomena. It also foreshadows the importance of transitioning into a coupled cycling mode in the evolution of multicellularity.

Funding Statement

This study was supported by NIDCR grant R01 DE015272 and Australian National Health and Medical Research Council grant 512524.3

Acknowledgments

General: We would like to thank Professor Georg Gottwald (Faculty of Science, University of Sydney) for reviewing the section on mathematical modeling and illuminating discussions and advice provided.

Disclosure statement

No potential conflict of interest was reported by the authors.

Data and materials availability

The authors declare that all data generated or analyzed during this study are included within the article and its supplementary information files.

Supplementary material

Supplemental data for this article can be accessed here