An active learning framework for enhancing identification of non-artifactual intracranial pressure waveforms

Abstract

Intracranial pressure (ICP) is an important and established clinical measurement that is used in the management of severe acute brain injury. ICP waveforms are usually triphasic and are susceptible to artifact because of transient catheter malfunction or routine patient care. Existing methods for artifact detection include threshold-based, stability-based, or template matching, and result in higher false positives (when there is variability in the ICP waveforms) or higher false negatives (when the ICP waveforms lack complete triphasic components but are valid). We hypothesized that artifact labeling of ICP waveforms can be optimized by an active learning approach which includes interactive querying of domain experts to identify a manageable number of informative training examples. The resulting active learning based framework identified non-artifactual ICP pulses with a superior AUC of 0.96 ± 0.012, compared to existing methods: template matching (AUC: 0.71 ± 0.04), ICP stability (AUC: 0.51 ± 0.036) and threshold-based (AUC: 0.5 ± 0.02).

1. Introduction

Intracranial pressure (ICP) monitoring is used to guide the management of patients with acute brain injury at risk for elevated ICP based on clinical and imaging features [1]. 37,000 patients a year receive an external ventricular drain (EVD) in the setting of acute hydrocephalus in the US, generating in-hospital charges of $151,672 per patient, or $5.6 billion dollars a year [2]. Beyond the mean value of ICP, ICP- derived features can hold significant importance in the management of acute brain injury. Among these include cerebral perfusion pressure (CPP) [3], continuous ICP waveform assessment [4], and indices derived from ICP waveforms such as pressure reactivity index (PRx), pulse amplitude index (PAx), and correlation between pulse amplitude and CPP (RAC) [5]. Active areas of investigation using analyses on ICP waveform morphology include: hydrocephalus shunt response in adults [6–10] and children [11], prediction of ICP [12,13], prediction of metabolic crises [14,15], prognosis following traumatic brain injury [16–19], prediction of intrcranial hypertension [20] and others [21–24].

There are many centers investigating the use of ICP waveform analysis; review articles detail this pre-clinical work [25,26]. The limitations to translating this technique into the clinical setting include acquiring the data from the invasive intracranial sensor and obtaining artifact free ICP waveforms [25]. In the pursuit of enabling translation of ICP waveform analysis into clinical setting, inherent challenges of artifacts must be addressed. These artifacts can be categorized as high frequency or low frequency noise. High frequency noise is introduced from devices and amplifiers, whereas low frequency noise is introduced by the complex patient environment [27,28]. Low frequency noise is embedded in the signal itself. Manual artifact removal can introduce variability from multiple raters and limit large-scale implementation.

Few methods currently exist to automate true ICP waveform identification. Template matching (TM) [28] involves creation of a reference library of valid ICP pulses, and determines true ICP waveform based on the correlation of the pulse with the reference library. The benefit of a reference library powering automated waveform identification is its consistency (as opposed to the variability of a human or manual rater). However, unless the library can be guaranteed to be exhaustive, it can incorrectly label true ICP waveforms as artifact. The reference library approach was embedded in a software package whose purpose was to quantify ICP waveform, a process highly dependent on 3 sub-peak (triphasic waveform) detection. This excludes the wide range of ICP waveforms that may not present with all 3 peaks, but are not artifactual (Figure 1). The use of this automated method would be too restrictive for practical uses, such as determination of continuous CPP, PRx, PAx, and RAC. In the non-artifactual pulse recognition algorithm reliant on ICP stability (IS) [27], true ICP is identified by comparing the mean amplitude and duration of pulse under investigation with the mean amplitude and duration of a double window comprised of three previous and three future pulse waves. The limitation with this method is that when all seven pulses are artifactual, the pulse under investigation would be identified as true ICP. Additionally, this algorithm will label true ICP as an artifact when there is variability in the ICP waveforms. A threshold-based algorithm (TB) [29] utilizes 6-second windows to compute mean ICP wave amplitude and mean ICP wave latency. It identifies the single wave as a true ICP if the wave amplitude is between 1.0 and 35.0 mmHg and latency between 0.08 and 0.40 s. The choice of the thresholds will considerably affect the identification of the ICP waveform. The authors of this approach tried different thresholds through visual inspection. Manual inspection of waveforms to set thresholds defeats the purpose of an automated analysis; this would be inhibitory for real-time monitoring.

Figure 1.

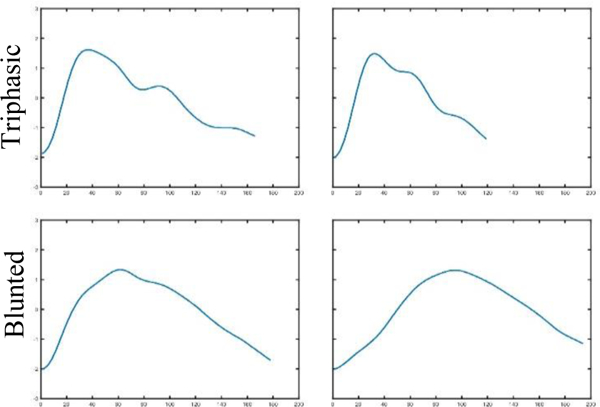
Examples of non-artifactual ICP waveforms

We propose an active learning approach to create a mathematical model of true ICP, one that is not limited to a curated reference library, a comparison of prior and future ICP waveforms, or a reliance on preset thresholds. Active learning is a semi-supervised technique in which a learning algorithm interactively queries data that are then labeled by an expert. It was a logical choice to other learning models in the absence of ground truth labeled data. Active learning is a principled approach to generating labeled data in an efficient way. Because not all training examples are equally useful for classification, the rationale for active learning is that a model can perform better despite training on fewer labeled data if the algorithm itself can choose the data on which it trains [30]. The method provides an appealing balance between expert-driven specificity and machine-driven efficiency by providing physicians with only the most influential waveforms to label, i.e. the data closest to the theoretical line between artifact and true measurement. It provides a platform for expert scrutiny of individual waveforms without wasting resources evaluating empirically similar samples. Active learning algorithms have found success in several domains, like detection of buried unexploded ordnance [31], classification of endothelial cells in tumors [32], text classification [33,34], microarray analysis [35], and recommender systems [36]. Our hypothesis is that this approach will result in a more accurate labeling of true ICP waveforms, which is correctly inclusive of abnormal but non-artifactual ICP.

2. Methods

2.1. Study Population

We studied consecutive subjects who were admitted to the neurointensive care unit between March 2016 and August 2017. This was part of an observational cohort study approved by the Columbia University Medical Center Institutional Review Board. We included subjects who had external ventricular drains and ICP waveforms transduced for at least one clamp trial before either EVD removal or permanent shunt placement. ICP signal was captured during 47 clamp trials (1160 hours) in total from 34 patients. All waveform data was collected at 125Hz using ICM Plus software (University of Cambridge, Cambridge Enterprise, Cambridge, UK, http://www.neurosurg.cam.ac.uk/icmplus).

2.2. Overall study design

We compared the performance of an active learning approach against the existing template matching (TM), ICP stability (IS), and threshold-based (TB) approaches for true ICP waveform labeling. First, we used a validated technique, Morphological Clustering Analysis of ICP Pulse (MOCAIP)[28], to detect dominant pulses in all ICP data. We extracted 126,725 dominant pulses. The sample size required for 95% confidence level, with 7% margin of error with a population size of 126,725 is 196. Therefore, we randomly selected 200 samples for a test set, and used the remaining for a training set. Because ambiguity exists in identifying abnormal but non-artifactual ICP waveform, we had three experts (Rater 1, Rater 2, Rater 3) separately label the 200 sample test set as true ICP vs artifact. We used Cohen’s Kappa statistic for agreement between a) manually labeled test dataset annotated by three raters, b) labels classified by active learning models on the test set (200 waveforms) c), labels classified by active learning models on the unlabeled dataset (126,525 waveforms). Interpretation of kappa coefficient was done according to the one proposed by Viera et al. [37] summarized in Table I.

TABLE I.

SUMMARY OF KAPPA COEFFICIENT

Kappa (κ)	Agreement
<0	Less than chance agreement
0.01–0.2	Slight agreement
0.21–0.4	Fair agreement
0.41–0.6	Moderate agreement
0.61–0.8	Substantial agreement
0.81–0.99	Almost perfect agreement

Lastly, we compared the three approaches (TM, IS, and TB algorithms) to our active learning approach for ICP waveform labeling. For template matching, we used the reference library that was created within MOCAIP [28] (shared by X.H.) to label ICP waveforms in our test set. For the ICP stability and threshold-based algorithms, we replicated the methods in Calisto et al. [27] and Eide et al. [29] to label ICP waveforms in our test set. For active learning, we built the classifier on the training dataset and applied it to our test set. We compared the four algorithms with area under the receiver operating curve (AUC), correct classification rate (CCR), positive predictive value (PPV), and negative predictive value (NPV). ). In addition to the above metrics, we have also computed partial area under the receiver operative curve (pAUC). pAUCs are most useful when only certain regions are of interest. For example, by constraining for specificity >= 0.9 we are assessing whether the false positive rates have been minimized. Likewise, by constraining for Sensitivity >=0.9 we are assessing if true positive rates are maximized.

2.3. Detection of dominant ICP pulse using Morphological Clustering Analysis of ICP Pulse (MOCAIP)

Dominant pulse extraction [28] consists of two components. The first step is identification of individual ICP pulses using the QRS complexes in the electrocardiogram (ECG) signal. The quantization noise is a well-known issue for typical ICP recording. Poor quality of ICP waveform severely hamper the feasibility of conducting the analysis of morphological changes of ICP pulses. A sensible trade-off can be made to conduct the analysis of ICP pulse morphology by not using individual pulse but rather using a representative cleaner pulse to be extracted from a sequence of consecutive raw ICP pulses. The second step is hierarchical clustering in short time segments (30 seconds), where raw ICP pulses are clustered based on their morphological distance. The largest cluster is identified and an average ICP pulse (the “dominant pulse”) is obtained from this cluster.

2.4. Approach 1: Template Matching for valid ICP waveform detection (TM)

The dominant pulse is compared to a static reference library of expert-validated ICP pulses to support the recognition of non-artifactual ICP pulses. A dominant pulse is judged to be a non-artifactual, if the pulse correlates with any of the reference ICP pulses with a correlation coefficient greater than a threshold of 0.82. For the waveforms x_i and y_i of length n and with mean values $\overline{\mathcal{X}}$ and $\overline{y}$ , the correlation coefficient was computed as,

$$r=\frac{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

Pulse was identified as true ICP if r > 0.82.

2.5. Approach 2: ICP Stability algorithm for non-artifactual pulse recognition (IS)

The amplitude (A_i) and duration (P_i) of the dominant pulse is compared with the mean amplitude and duration of a double window comprising of three previous and three future pulse waves A_m and P_M, where

$$A_M=\frac{{\sum }_{j=-3}^{-1}{A}_{i+j}+{\sum }_{j=1}^3{A}_{i+j}}{6},$$

$$P_M=\frac{{\sum }_{j=-3}^{-1}{P}_{i+j}+{\sum }_{j=1}^3{P}_{i+j}}{6}$$

Pulse is identified as a valid or true ICP if

$$\left|P_i-P_M\right|\le 15\%.P_M$$

and

$$\left|A_i-A_M\right|\le 10\%.A_M.$$

2.6. Approach 3: Threshold-based single wave criteria (TB)

The dominant pulse is marked as a true ICP if the wave amplitude is between 1.0 and 35.0 mmHg and latency between 0.08 and 0.40s. Wave amplitude (W_A) is the pressure difference between the starting diastolic minimum pressure and systolic maximum pressure. Wave latency (W_L) is the time interval when the pressures change from diastolic minimum pressure to systolic maximum pressure.

Pulse is identified as valid or true ICP if

$$\text{1}mmHg\text{<}{W}_A\text{< 35}mmHg$$

and

$$\text{0}.08s\text{<}{W}_L\text{<0}\text{.40}s$$

2.7. Proposed Approach: Active Learning for valid ICP waveform detection (AL)

The dominant pulse of a 30 second ICP segment, identified by MOCAIP, is used as the feature vector represented by x_i. Each dominant pulse in this binary classification can be associated as either a valid waveform (+1) or an artifact (−1). A logistic regression model is written as,

$$P\left(y_i|x_i\right)=\sigma \left(y_i{w}^T{x}_i\right)$$

$$\sigma (\gamma )=\frac{1}{1+e^{-\gamma }}$$

Where P(.) denotes the probability of an event and w is a vector of classifier parameters that need to be estimated. Assuming the features are independently and identically distributed (iids), the log-likelihood function can be written as

$$l(w)={\Sigma }_{i=1}^{N}ln\sigma \left(y_i{w}^T{x}_i\right)$$

and with enough labeled examples, w_optimai is solved by maximizing log-likelihood function as:

$$w_{\text{optimal}}=arg\underset{w}{max}{\sum }_{i=1}^{N}ln\sigma \left(y_i{w}^T{x}_i\right)$$

The selection of the training examples proceeds in a sequential manner. The proposed framework uses variance reduction methods, where examples that maximize the determinant of the Fisher information matrix Q [38] are queried for their labels. By definition of Fisher information matrix [38], we have

$$Q=E_y\{\frac{\partial l}{\partial w}\frac{\partial l^T}{\partial w}\}$$

The inverse of the determinant of Fisher information (|det(Q)|⁻¹ ) sets a lower bound on the variance of the model’s parameter estimates [38,39]. In other words, to minimize the variances over its parameter estimates, the algorithm should select the data and query the user for the input label that will maximize the Fisher information[32].

Figure 2 shows the graphical user interface (GUI) that queries the experts for input labels. Three experts (Rater 1, Rater 2, Rater 3) separately trained an active learning model. With visual access to the entire training dataset (126,525 examples), the expert selects one example each of a valid ICP pulse and of an artifact; this is the initial training example for the current classification task. The algorithm sifts through the training data, and provides the expert with one waveform that results in the maximum information computed via the Fisher information matrix. The expert then labels the suggested waveform as either a valid ICP pulse or as an artifact. Based on the response of the expert, the algorithm then updates its parameters and computes the most informative waveform for the expert to label for the next iteration. The limitation of a machine learning model is that it can not remove all the possible artifacts; we mitigate this limitation by presenting the online information gain of the model, with the assumption that as information gain decreases, the model is closer to maximally learning inherent characteristics of ICP waveforms (vs artifact). The algorithm training is terminated when the gradient of information gain plateaus. We evaluated the performance of the classifiers using c-statistics, precision recall, correct classification rate, positive predicted value, and negative predicted value [40] on a test dataset that was not used for model building. The GUI displays the iterative performance of the model on the test set, and displays the results on the unlabeled training data as shown in the Figure 2. Each expert sits through multiple active learning sessions, to demonstrate the consistency of the model. The consistency of intra-individual inter-session learning is measured by the mean and standard deviation of the performance metrics. The performance of each active learning model for inter-rater agreement is compared with Cohen’s Kappa statistic. Interpretation of kappa coefficient was done according to the one proposed by Viera et al. [37] summarized in Table I.

Figure 2 :

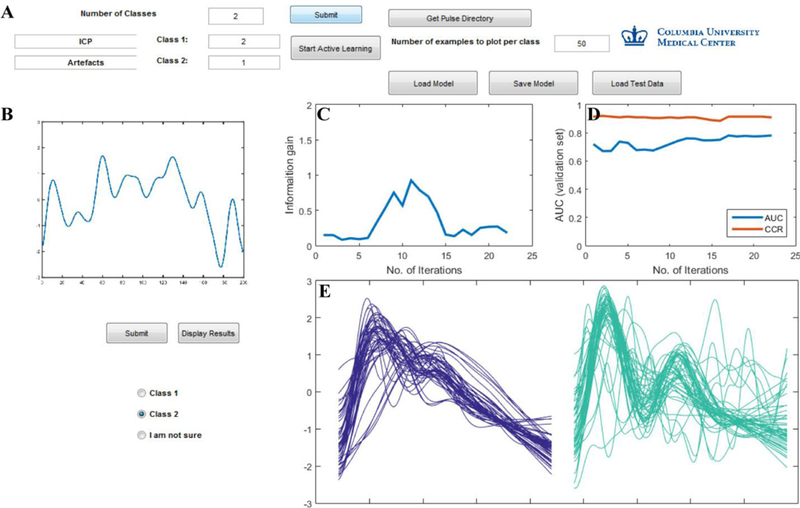
Graphical User Interface (GUI) to train the active learning model. (A) Model inputs: number of classes, one example of valid ICP pulse and artifact; ability to save the current model or load an existing model. (B) Pulse displayed on the GUI for the trainer to label as either class 1 (valid ICP), class 2 (artifact) or “I am not sure”. (C) Plot displaying information gain (D) Plot displaying area under the curve (AUC) and correct classification rate (CCR) on the test data updated based on the trainers input for every iteration. (E) The results of the AL model on the training dataset is displayed for two classes in purple (valid ICP) and green (artifacts).

3. Results

From March 2016 to August 2017, 34 patients (mean age 57 years +/− 12.9, 21 female (61.8%)) with ICP waveform data from EVDs were enrolled in the study. Twelve were admitted for intracranial hemorrhage (ICH, 35.3%), 14 for subarachnoid hemorrhage (SAH, 41.2%), 1 for traumatic brain injury (TBI, 2.9%) and 7 for other diagnoses (20.6%). The average length of stay was 18.9 +/− 9.7 days, with average length of clamp trial 23.5 +/‒ 19.1 hours. We extracted 126,725 dominant pulses; of those, 200 dominant pulses were set as the test dataset. We identified an additional 5 patients (external to the 34) not used in the test or training process and reported the performance of models on this prospective validation dataset. (Supplementary Figure A 1).

3.1. Test Set

Of the 200 manually labeled ICPs in the test dataset, Rater 1 identified 20, Rater 3 and Rater 2 identified 21 artifacts. The remaining were identified as true ICP. They agreed among themselves 91% of the time. The agreement was quantified by pair-wise kappa statistics. The agreement between Raters 1 & 2 and Raters 3 & 2 was “substantial” while the agreement between Raters 1 & 3 was moderate (Figure 3). The kappa statistics on the unlabeled training set (126,525 waveforms) were substantial (0.75, 0.77) to “almost perfect” (0.87) (Table I).

Figure 3:

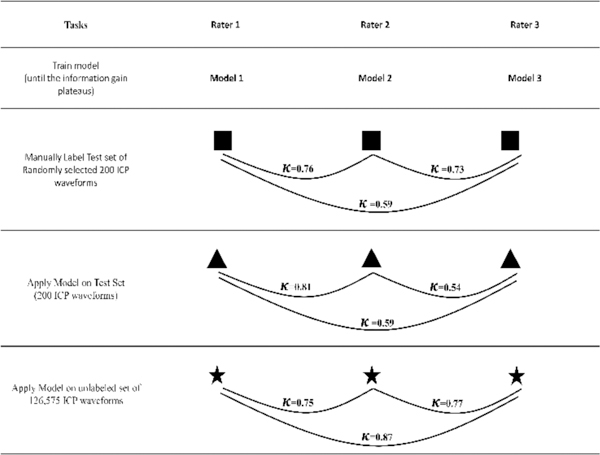
Inter-rater agreement quantified by kappa statistics between manually labeled (200 waveforms) datasets labeled by three raters; agreement of the individually trained models on their own test sets (200 waveforms) and the agreement of the models on the larger unlabeled dataset (126,575 waveforms).

3.2. Approaches 1–3: Template Matching, ICP stability, and Threshold-Based non-artifactual pulse recognition algorithm for valid ICP waveform detection

The AUCs and CCRs for template matching (AUC – Rater 1: 0.75, Rater 2: 0.67, Rater 3: 0.7; CCR – Rater 1: 0.81, Rater 2: 0.8, Rater 3: 0.8) were higher compared to the ICP stability approach (AUC – Rater 1: 0.55, Rater 2: 0.48, Rater 3: 0.5; CCR – Rater 1: 0.69, Rater 2: 0.71, Rater 3: 0.71) and threshold-based approach (AUC - Rater 1: 0.5, Rater 2: 0.52, Rater 3: 0.48; CCR – Rater 1: 0.63, Rater 2: 0.62, Rater 3: 0.63). AUC curves are included in Supplementary Figure A 2. Positive predictive values (PPV) and negative predictive values (NPV) were also higher for template matching (PPV – Rater 1: 0.86, Rater 2: 0.86, Rater 3: 0.86; NPV – Rater 1: 0.35, Rater 2: 0.32, Rater 3: 0.33) compared to the ICP stability approach (PPV - Rater 1: 0.75, Rater 2: 0.76, Rater 3: 0.76; NPV - Rater 1: 0.15, Rater 2: 0.24, Rater 3: 0.24) and threshold-based approach (PPV – Rater 1: 0.66, Rater 2: 0. 65, Rater 3: 0.66; NPV – Rater 1: 0.35, Rater 2: 0.32, Rater 3: 0.38) (Table II). The performance metrics under the two constraints of sensitivity ≥ 0.9 and specificity ≥ 0.9 were also higher for template matching (pAUC – constrained sen.: 0.033±0.001, pAUC – constrained spec.: 0.031±0.019) when compared to ICP stability (pAUC – constrained sen.: 0.004±0.001, Pauc – constrained spec.: 0.006±0.002) and threshold based (pAUC – constrained sen.: 0.005±0.001, pAUC – constrained spec.: 0.005±0.0). (Table III) (Table A I).

TABLE II.

PERFORMANCE METRICS FOR THREE DIFFERENT METHODS ON TEST DATASETS CREATED BY THREE DOMAIN EXPERTS (RATER 1, RATER 2, RATER 3)

Users	AUC	AU-PRC	CCR	Sensitivity	Specificity	PPV	NVP
Rater 1 - AL	0.95 +/−0.01	0.99 +/−0	0.94 +/−0.01	0.97 +/−0.01	0.69 +/−0.05	0.96 +/−0.01	0.75 +/−0.05
Rater 1 - TM	0.75	0.96	0.81	0.92	0.22	0.86	0.35
Rater 1 - IS	0.55	0.69	0.69	0.89	0.06	0.75	0.15
Rater 1 - TB	0.5	0.59	0.63	0.9	0.1	0.66	0.35
Rater 2 - AL	0.97 +/−0.01	0.99 +/−0	0.94 +/−0.02	0.97 +/−0.01	0.75 +/−0.09	0.97 +/−0.01	0.74 +/−0.05
Rater 2 - TM	0.67	0.94	0.8	0.91	0.22	0.86	0.32
Rater 2 - IS	0.48	0.67	0.71	0.89	0.1	0.76	0.24
Rater 2 - TB	0.52	0.58	0.62	0.89	0.1	0.65	0.32
Rater 3 - AL	0.95 +/−0.02	0.99 +/−0.01	0.93 +/−0.02	0.97 +/−0.01	0.66 +/−0.11	0.95 +/−0.03	0.76 +/−0.1
Rater 3 - TM	0.7	0.95	0.8	0.92	0.22	0.86	0.33
Rater 3 - IS	0.5	0.68	0.71	0.89	0.1	0.76	0.24
Rater 3 - TB	0.48	0.59	0.63	0.9	0.12	0.66	0.38

AL: Active Learning, TM: Template Matching, IS: ICPStability, TB: Threshold-Based

AUC: Area under receiver operating curve, AU-PRC: Area under precision recall curve

CCR: Correct classification Rate, PPV: Positive Predictive Value, NPV: Negative Predictive Value

TABLE III.

DATASETS PERFORMANCE AT SENSITIVITY ≥ 0.9 AND SPECIFICITY ≥ 0.9 FOR THREE DIFFERENT METHODS ON TEST

	Performance at Sensitivity ≥ 0.9						Performance at Specificity ≥ 0.9
Method	PAUC	CCR	Sen.	Spec.	PPV	NPV	PAUC	CCR	Sen.	Spec.	PPV	NPV
AL	0.072±0.005	0.899±0.005	0.903±0	0.844±0.051	0.980±0.006	0.503±0.015	0.072±0.007	0.855±0.045	0.845±0.062	0.903±0	0.988±0.001	0.427±0.096
TM	0.033±0.001	0.845±0.001	0.903±0.003	0.339±0.009	0.922±0.003	0.288±0.007	0.031±0.019	0.479±0.114	0.430±0.129	0.903±0.003	0.973±0.008	0.158±0.027
IS	0.004±0.001	0.896±0.003	1.0±0.0	0.0 ±0.0	0.896±0.003	NA	0.006±0.002	0.438±0.235	0.418±0.300	0.617±0.331	0.910±0.0025	0.108±0.004
TB	0.005±0.001	0.896±0.003	1.0±0.0	0.0±0.0	0.896±0.003	NA	0.005±0.0	0.546±0.142	0.554±0.179	0.466±0.175	0.900±0.001	0.108±0.008

AL: Active Learning, TM: Template Matching, IS: ICPStability, TB: Threshold-Based

Sen.: Sensitivity, Spec.: Specificity

PAUC: Partial Area under receiver operating curve, AU-PRC: Area under precision recall curve

CCR: Correct classification Rate, PPV: Positive Predictive Value, NPV: Negative Predictive Value

3.3. Our Approach: Active Learning for valid ICP waveform detection

The AUCs (Rater 1: 0.95 +/‒ 0.01, Rater 2: 0.97+/‒ 0.01, Rater 3: 0.95+/‒ 0.02), CCRs (Rater 1: 0.94 +/‒ 0.01, Rater 2: 0.94+/‒0.02, Rater 3: 0.93+/‒ 0.02), PPVs (Rater 1: 0.96 +/‒ 0.01, Rater 2: 0.97+/‒ 0.01, Rater 3: 0.95+/‒ 0.03) and NPVs (Rater 1: 0.75 +/‒ 0.05, Rater 2: 0.74+/‒ 0.05, Rater 3: 0. 76+/‒ 0.10) (Table II) of the active learning model were higher compared to the template matching, ICP stability, and threshold-based non-artifactual pulse recognition algorithms (Figure 4) (Table II). The performance metrics under the two constraints of sensitivity ≥ 0.9 and specificity ≥ 0.9 (pAUC – constrained sen.: 0.072±0.005, pAUC - constrained spec.: 0.072±0.007) were also higher when compared to the TM, IS and TB methods. (Table III) (Table A I). The number of training examples at which the performance metric plateaued with active learning was around 50 for Rater 1 and Rater 3 and 100 for Rater 2 (Figure 4). The agreement was quantified by pairwise kappa statistics, the agreement between (Rater 1 Rater 2), was “almost perfect” while the agreements between (Rater 1 Rater 3) and (Rater 3 Rater 2) were moderate.

Figure 4.

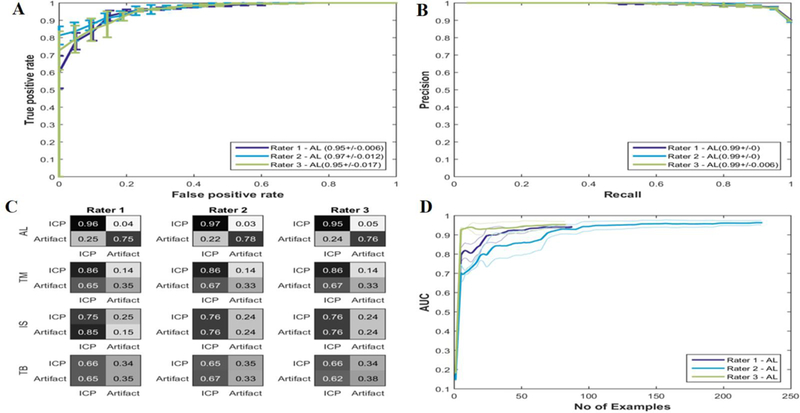
Results of the classifier trained by three different users. (A) Area under the receiver operating curve (AUC) (B) Area under precision recall curve (AU-PRC) and (C) confusion matrices for 3 different ICP recognition algorithms (AL : Active learning, TM : Template matching and IS : ICP stability algorithms). (D) The AUCs of the training for active learning is plotted against the number of examples selected sequentially. The active learning approach took about 60 examples to reach its peak performance.

3.4. Qualitative Comparison of ICP waveforms

We looked at the false negatives and false positives for each method (Supplementary Figure A 3), to compare the waveforms that were labeled incorrectly. The template matching, ICP stability, and threshold-based approaches labeled blunted ICPs (without clear P1, P2, P3) as artifact. The threshold-based approach also labeled triphasic waves as artifacts. For active learning models, there were a few instances of blunted ICPs that were labeled as artifact but the total number of such cases were lower than that of the other methods (Supplementary Figure A 3). The threshold-based approach has the highest number of false positives and equally high false negatives.

4. Discussion

The active learning model performed better than the existing models for non-artifactual ICP waveform labeling. We have shown that an active learning framework to label non- artifactual ICP waveforms is feasible. The advantage of this approach is the correct inclusion of non-artifactual waves that lack complete triphasic waveforms, and does not require a large labeled dataset (that is not necessarily representative of the spectrum of valid waveforms) as in the case of template matching. Unlike the ICP stability approach, the proposed framework is not tricked by the variability in ICP waveforms, and has fewer false negatives. The AL approach is also not tricked by long stretches of artifact which can lead to false positives with the ICP stability approach. The threshold-based approach has the highest false positive rate among all the approaches; this is because artifacts in our dataset have the same mean amplitude and latency as valid ICP. The threshold-based approach also has high false negative rates because valid ICP waveforms had long wave latencies outside the threshold (0.08 <W_L <0.4) (Supplementary Figure A 4). Thus, this method is sensitive to changes in the threshold values. For these reasons, the proposed active learning framework is likely to be more clinically useful in the ICU than existing algorithms to support real-time ICP-derived analytics.