Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2019 Jun 10;10(30):7233–7245. doi: 10.1039/c9sc01743g

Covalency and magnetic anisotropy in lanthanide single molecule magnets: the DyDOTA archetype†

Matteo Briganti a,c, Guglielmo Fernandez Garcia a,b, Julie Jung b,‡, Roberta Sessoli a, Boris Le Guennic b,✉, Federico Totti a,✉
PMCID: PMC6685353  PMID: 31588292

graphic file with name c9sc01743g-ga.jpgThe unexpected covalent contribution in the DOTADy-OH2 bond revealed by ab initio calculations of the easy axis of magnetization through simple H2O rotations.

Abstract

Lanthanide ions when complexed by polyamino-polycarboxylate chelators form a class of compounds of paramount importance in several research and technological areas, particularly in the fields of magnetic resonance and molecular magnetism. Indeed, the gadolinium derivative is one of the most employed contrast agents for magnetic resonance imaging while the dysprosium one belongs to a new generation of contrast agents for T2-weighted MRI. In molecular magnetism, Single Molecule Magnets (SMMs) containing lanthanide ions have become readily popular in the chemistry and physics communities since record energy barriers to the reversal of magnetization were reported. The success of lanthanide complexes lies in their large anisotropy due to the contribution of the unquenched orbital angular momentum. However, only a few efforts have been made so far to understand how the f-orbitals can be influenced by the surrounding ligands. The outcomes have been rationalized using mere electrostatic perturbation models. In the archetype compound [Na{Dy(DOTA) (H2O)}]·4H2O (Na{DyDOTA}·4H2O) an unexpected easy axis of magnetization perpendicular to the pseudo-tetragonal axis of the molecule was found. Interestingly, a dependency of the orientation of the principal magnetization axis on the simple rotation of the coordinating apical water molecule (AWM) – highly relevant for MRI contrast – around the Dy-OAWM bond was predicted by ab initio calculations, too. However, such a behaviour has been contested in a subsequent paper justifying their conclusions on pure electrostatic assumptions. In this paper, we want to shed some light on the nature of the subtle effects induced by the water molecule on the magnetic properties of the DyDOTA archetype complex. Therefore, we have critically reviewed the structural models already published in the literature along with new ones, showing how the easy axis orientation can dangerously depend on the chosen model. The different computed behaviors of the orientation of the easy axis of magnetization have been rationalized as a function of the energy gap between the ground and the first excited doublet. Magneto-structural correlations together with a mapping of the electrostatic potential generated by the ligands around the Dy(iii) ion through a multipolar expansion have also been used to evidence and quantify the covalent contribution of the AWM orbitals.

Introduction

Lanthanide ions when complexed by polyamino-polycarboxylate chelators form a class of compounds of paramount importance in several research and technological areas, particularly in the fields of magnetic resonance1 and molecular magnetism.2–4 One of the paradigmatic ligands of this class of complexes is the twelve-membered tetra-azamacrocyclic H4DOTA (1,4,7,10-tetraazacyclododecane-1,4,7,10-N,N′,N′′,N′′′-tetraacetic acid). In its fully deprotonated form, DOTA4–, it yields thermodynamically and kinetically stable compounds5 with the whole series of trivalent lanthanide ions Ln3+ giving a capped square antiprismatic coordination geometry (coordination number 9). The rare earth ion is sandwiched between two parallel square faces, one formed by the ligand's four nitrogen atoms and the other by four oxygen atoms of the four acetate groups. The ninth coordination site along the pseudo C4 axis is occupied by a non-innocent apical water molecule (AWM) which contributes to the unique properties of this series of complexes. Indeed, this is the reason why the gadolinium derivative (commercialized as DOTAREM) is one of the most employed contrast agents for magnetic resonance imaging (MRI), along with other complexes such as [Gd(DTPA)(H2O)]2– (DTPA = diethylenetriamine penta-acetic acid). Moreover, ligands derived from DOTA are widely employed and investigated in order to improve selectivity and contrast enhancement.6–8

The exchange of the AWM between the complex and the solvent selectively increases the longitudinal relaxation rate of the water protons in certain tissues,9 a principle on which the T1-weighted magnetic resonance imaging (MRI) is based. On the other hand, complexes of the series based on anisotropic lanthanides, like dysprosium, are promising contrast agents for T2-weighted MRI, a new generation of MRI contrast agents10,11 exploiting also new MRI contrast mechanisms such as the chemical exchange saturation transfer (CEST).12 The access to the magnetic anisotropy tensor is also an important piece of information for interpreting the solution and solid-state NMR of paramagnetic proteins. [LnDOTA]– complexes already displayed good qualities for assessing the structure of proteins by NMR spectroscopy.13–15 Indeed, the pseudo-contact shift depends on the position of the atom with respect to the orientation of the magnetic susceptibility tensor and the distance from the paramagnetic center, and its effect is felt on the local environment up to 40 Å.

In the field of molecular magnetism the series of [Ln(DOTA)(H2O)]– was extensively studied3,4 as one of the pioneer complexes of lanthanide based Single Molecule Magnets (SMMs).16 SMMs are a class of compounds that present below a certain temperature, called the blocking temperature, Tblock, slow relaxation of the magnetization and eventually the opening of a hysteresis loop.17 These properties arise from the electronic structure of the isolated molecule and not from long-range interactions like in classical magnets. The rate of this process is modeled with an Arrhenius-like law τ = τ0 exp(U/kBT), where τ is the mean time necessary for the spin to overcome the barrier U. Great efforts were devoted to increasing U, the relaxation time and the blocking temperature in order to employ these systems in real devices such as magnetic memories of molecular dimensions,18–20 quantum computers,21,22 and electronic devices based on molecular spintronics.23–25

The pioneering work of Ishikawa26 demonstrated that in mononuclear complexes containing lanthanide ions anisotropy barriers of hundreds of K could be reached, an order of magnitude higher than the ones observed so far. Generally, the contribution to the coordination bonding of the 4f orbitals, where the unpaired electrons in Ln(iii) ions reside, is not as significant as for the 3d orbitals due to their ‘core’ character. Therefore, their orbital angular momentum is largely unquenched causing a rise in magnetic anisotropy of the first order. Despite record energy barriers of thousands of K, the blocking temperatures remained around the temperature of liquid helium, confirming the complex relation between the anisotropy barrier and the blocking temperature and the geometry. On this topic some light has been shed in some recent papers both for lanthanide and transition metal mono-nuclear compounds.27–31 Very recently, new successful efforts have provided blocking temperatures around the nitrogen boiling point.30,32,33 An important contribution to the achievements in the field has been given by computational approaches.34,35 In order to rationalize the properties of lanthanide complexes on a computational basis, in the last ten years ab initio methods based on Complete Active Space Self Consistent Field36 (CASSCF) with the introduction of Spin–Orbit (SO) coupling through the Complete Active Space State Interaction37 (CASSI) proved to be able to reproduce experimental findings coming from different experimental techniques such as DC38 and AC magnetometry,39,40 electron paramagnetic resonance,41,42 cantilever torque magnetometry,39,43,44 and inelastic neutron scattering.45,46

However, a clear understanding of some key aspects is still lacking, first of all, a reliable reproduction of the ligand field around the lanthanide ion. In other words, the main challenge is finding how to correctly account for the electrostatic field and the covalent interactions between the f orbitals, the ligands and the crystal environment. Indeed, the idea that the 4f orbitals are not strongly involved in the coordination bond as their d orbital counterparts supported the idea that a rationalization of the magnetic anisotropy in lanthanide complexes could be based only on electrostatic considerations. Several attempts were made following this idea going from employing formal charges on the ligands47 or more sophisticated effective charge models.48 The common limitation of these approaches is the underestimation of covalent interactions, which are accountable only with the explicit calculation of the whole electronic structure of the complex. The role of each of the two contributions (covalent and electrostatic) can obviously vary from case to case but even if the former is expected to be, in general, smaller than the latter, the complete neglecting of it can be risky.49 Indeed, magnetic properties are really sensitive to small perturbations, like tiny deviations from idealized geometry49 or variations of the bond distances,50,51 i.e. to different combinations of electrostatic and covalent contributions.

In this framework, not only is the employment of the highest affordable level of calculation necessary but also the choice of molecular model is crucial because it can seriously affect the results. To make things even more complicated, a reliable reproduction of the crystal environment, i.e. the Madelung potential, becomes another key aspect. To our knowledge, only few attempts toward such a direction have been made.41,52–54 However, these attempts made use of gas-phase computed molecular point charges.

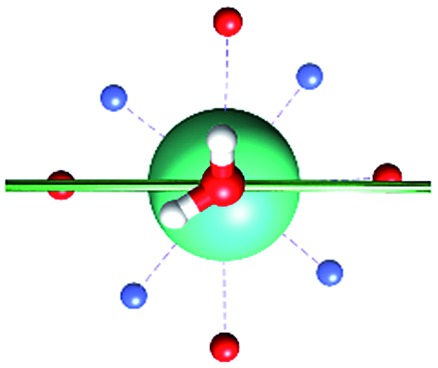
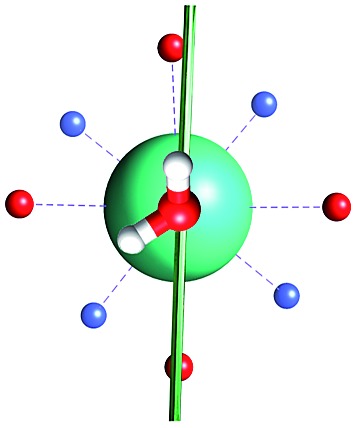
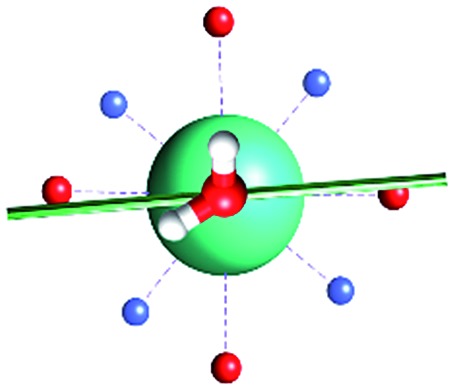
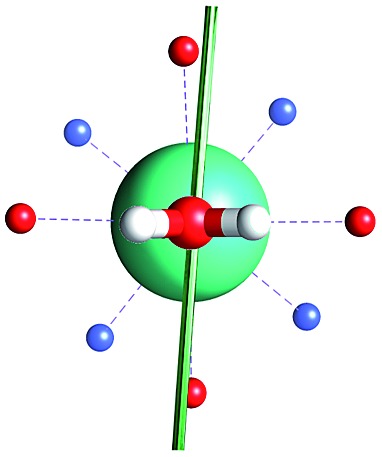
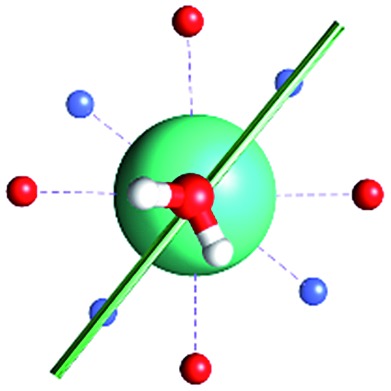
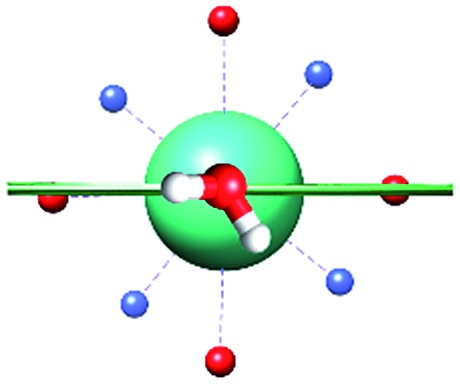
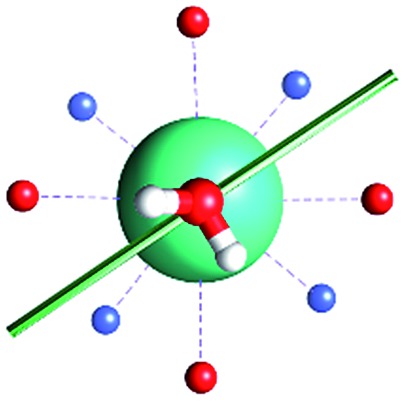
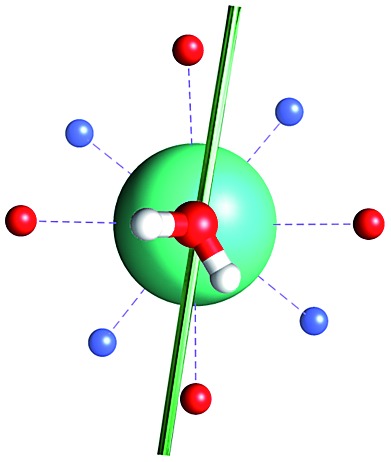
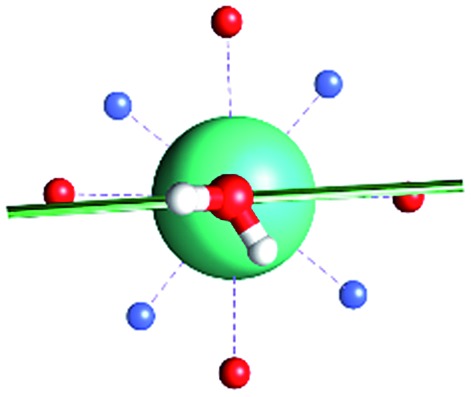
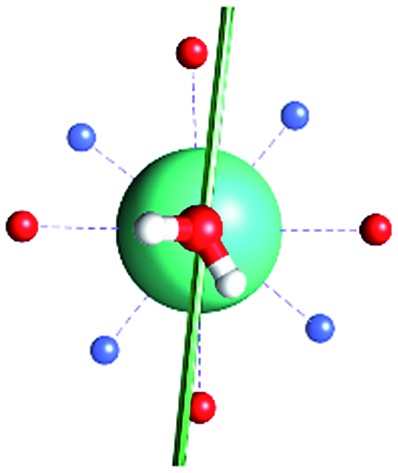
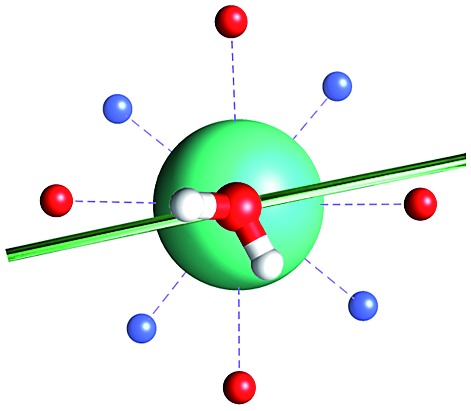
The archetype compound [Dy(DOTA)(H2O)]– complex (DyDOTA in the following), Fig. 1,2 is particularly suitable for the investigation of the interplay of all these contributions. Such a complex has been deeply characterized both at the computational and experimental levels.2,4,55 It presents a first coordination sphere with a pseudo-tetragonal symmetry, and for this reason either an easy axis of magnetization along the C4 or an easy-plane behavior in the four coordination DOTA oxygens could be expected. However, DyDOTA presents an easy axis of magnetic anisotropy which is perpendicular to the pseudo-tetragonal axis of the molecule. Interestingly, for the first time, a dependence of the orientation of the main magnetic axis as a function of a tiny structural modification was predicted by ab initio methods. Indeed, to reproduce the experimental data (direction and magnitude of the anisotropy axes and the magnetic multiplet energy ladder) a particular orientation of the apical water molecule (AWM)'s hydrogens was necessary. For this reason, it was supposed that there was an interplay between the electrostatic potential determined by the ligands and a small, but not negligible, covalent interaction between the dysprosium's f orbitals and the AWM's molecular orbitals.

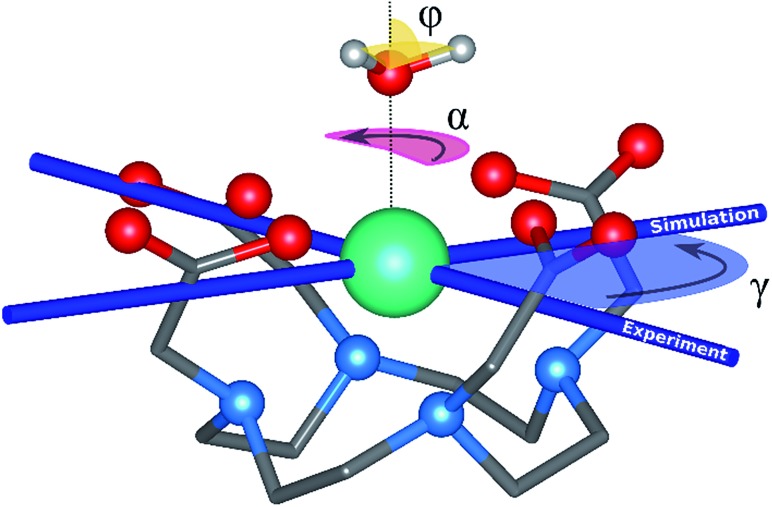
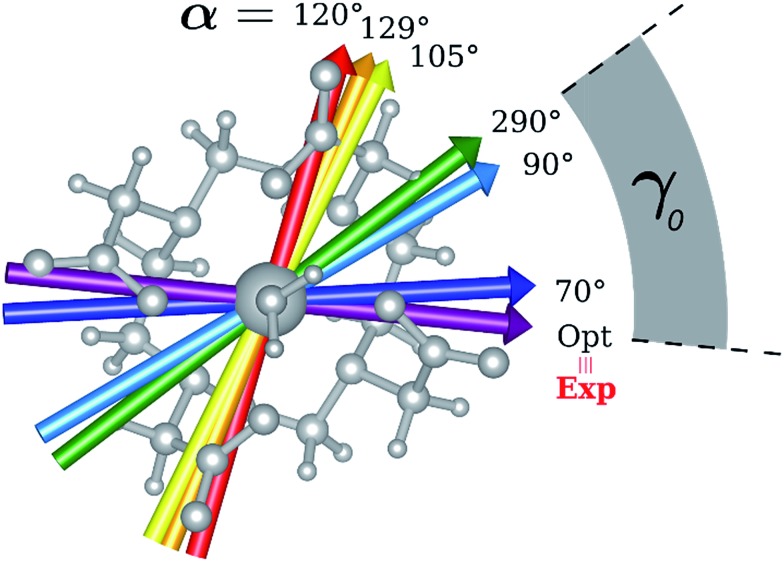
Fig. 1. Main geometrical parameters employed for magneto-structural correlations. α is the angle of rotation around the Dy-OAWM bond; γ0,1 represents the angles between the calculated and experimental easy-axis of magnetization for the ground and first excited Kramers' doublets; and φ is the angle between the Dy-OAWM bond and the plane of the water molecule. The dysprosium atom is coloured in light green, oxygen atoms in red, nitrogen atoms in cyan, carbon atoms in grey and hydrogen AWM atoms in white. Hydrogen atoms of DOTA were not reported for the sake of clarity.

Fig. 1

Open in a new tab

This uncommon behavior makes the computational study of this complex a hard but intriguing task. It offers an extraordinary possibility to gain insights into how to handle from a computational point of view the subtle equilibrium between covalent contributions and electrostatic field strength.

The different structural models proposed in the literature led to apparently contrasting results. Both the orientation of the AWM's protons and the extent of the number of atoms explicitly or implicitly considered in the model were analyzed in the original article by Cucinotta et al.2 The results showed a prominent role of the orientation of the AWM protons in determining the energy ladder and the directions of the anisotropy axes. On the other hand, Chilton et al.47 showed no influence arising from the AWM's orientation on the single ion magnetic anisotropy. The difference in the obtained results lies in the different models employed in the two articles, in particular, the inclusion of distinct coordination spheres surrounding the central [Dy(DOTA) (H2O)]– cluster, which can strongly affect the electrostatic field strength.

In summary, the aim of this work is two-fold: (i) to critically revise the model proposed so far in the literature to provide a general approach to model magnetic lanthanide-based complexes with a better description of the Madelung potential thanks to periodically computed point charges; (ii) to shed some light on the perennial question about the interplay between covalent and electrostatic contributions in f-coordination compounds.56 For these purposes the magnetic anisotropy tensor – which is a “pure” f orbital-originated observable – has been used as a reliable probe. It has been investigated here by performing a large variety of magneto-structural correlations involving different structural bonding parameters (rotations, stretching and bending) of the AWM and by an electrostatic multipolar expansion analysis.57–59

This work is focused on a single lanthanide derivative, but the conclusions and the proposed approach can be extended, in general, to other lanthanide based14 complexes and even beyond the solid state, including MRI relaxation mechanisms in solution.60,61 Indeed, even if in crystals the rotation of the water molecule is not allowed by supramolecular interactions, in solution this is not true: the water molecule is free to rotate and undergo the solvent exchange process. This could shed new light on the mechanism of the relaxation enhancement in solution in the presence of MRI contrast agents based on anisotropic lanthanide atoms.

Computational approach

All employed models are based on crystallographic structural data, with the exclusion of the two HAWM, which have been optimized at the DFT level for M1 and M2 models (see below and the Computational details). All models are shown and schematically described in Table 1 and Fig. 2 (see the ESI† for further details). The differences among the presented models arise from the number of explicit atoms considered at the highest computational level (QM) and the eventual addition of a different number of point charges (Table 1). For all of them the same computational protocol CASSCF/CASSI-SO along with all-electron basis sets for all the explicit atoms considered were used (Computational details). Rigid rotations of the apical water molecule were performed on all the presented models.

Table 1. Summary of the different structural models considered in this paper (M1–5) and the already published ones by Cucinotta et al.2 and Chilton's et al.47 For the colour code, refer to Fig. 2 .

Models [DyDOTAH2O]– (Inline graphic) 3 Na+ ions surrounding the DyDOTA complex (Inline graphic) Coord. sphere of 3 Na+ ions (Inline graphic) 4 Dy ions of neighbouring molecules (Inline graphic) All atoms of 2 neighbouring crystal cells (Inline graphic)
M1 Explicitly QM handled DDA point charges DDA point charges DDA point charges DDA point charges
M2/M2m Explicitly QM handled — — — —
M3 Explicitly QM handled Explicitly QM handled — — —
M4 Explicitly QM handled Explicitly QM handled 3(2HCOO– + H2O) — —
M5 Explicitly QM handled Explicitly QM handled 3(2HCOO– + H2O) DDA point charges —
Cucinotta et al.2 Model A/A′ Explicitly QM handled Explicitly QM handled 3(2HCOO– + H2O) Explicitly QM mimicked by Na+ ions —
Cucinotta et al.2 Model C Explicitly QM handled — — — —
Chilton et al.47 Explicitly QM handled Explicitly QM handled — — —
Open in a new tab

Fig. 2. Scheme of the different models employed. The different colors indicate different parts of the system modeled according to Table 1.

Fig. 2

Open in a new tab

Model 1, M1, was built based on the necessity to fulfill both chemical soundness (Fig. S1 and S2†) and an accurate representation of the electrostatic environment around the very sensitive Dy(iii) ion. Indeed, the most correct way to model a system as DyDOTA would be by considering it in its periodic environment. The problem of this approach is related to the impossibility of performing such a calculation at the level of accuracy afforded by the CASSCF/CASSI-SO approach. To overcome this problem we mimicked the first four neighbouring [Dy(DOTA)(H2O)]– units, the counterions and the co-crystallized water molecules with point charges, leaving a single [Dy(DOTA)(H2O)]– complex explicitly computed at the highest level of accuracy. Due to its a priori nature, i.e. without any arbitrary assumption about the extension of the geometry, we chose M1 as our reference model.

With the aim of reducing the computational effort and consequently testing a reliable but lighter ‘operative’ model, we reduced M1 to a different one consisting of only one [Dy(DOTA)(H2O)]– unit and two aldehydes mimicking the carbonyl groups of an adjacent DyDOTA molecule (Fig. S3†). M2m differs from the M2 model by the removal of the two aldehydes. M2 and M2m represent the most intuitive, and therefore, the simplest possible models. By the way, this type of model is widely used in the literature when a lanthanide complex is handled at the CASSCF/CASSI-SO level of approximation.39,62,63

In the unit cell, each DyDOTA complex is surrounded by three counter-ions. Model 3 (M3) has been designed to account for these three cations at their crystallographic positions (Fig. S4†). M3 was considered because it closely resembles the model used by Chilton et al.47

Model 4, M4, is obtained by adding to M3 four more formate anions and two water molecules around each of the three Na+ ions. The first coordination sphere of each Na+ ion is now complete (see also Fig. S5†). Finally, to reduce the charge unbalance in M4, the computed DFT point charges (see Computational details) of the four dysprosium ions belonging to the surrounding complexes were added (Fig. S6†) to it (M5). Such a model is very close to the Model A/A′ (total charge equal to 0) proposed by Cucinotta et al.2

Computational details

Geometry optimization of the positions of the two HAWM atoms in M1 and M2 was performed with the quantum chemistry package ORCA.64 For both models the dihedral angle φ between the plane of the water molecule and the Dy-OAWM bond (see Fig. 1) was computed to be 53.6° and was used throughout all the other models.

The unrestricted DFT/B3LYP65 functional, together with van der Waals empirical dispersion correction D3,66 has been used. VTZPP basis sets for all the atoms were chosen. Relativistic effects were accounted for by using the second-order Douglas–Kroll–Hess (DKH2) Hamiltonian. The spin multiplicity was set to six. The Def2-TZVPP basis set was employed for all the atoms except for the lanthanide atom where the SARC-TZV basis set67 was used.

To simulate the effect of the crystal environment on a larger scale than considering just few neighbouring atoms or pieces of adjacent DyDOTA complexes but still at a computationally affordable level, atomic point charges were added to the explicit models. Point charges were computed as density derived atomic point charges (DDAPC)68 obtained by a single point calculation on the [NaDy(DOTA)(H2O)]·4H2O unit cell using the PBE0 functional69 with periodic boundary conditions included. The software package CP2K70 based on a mixed Gaussian and plane wave71 (GPW) formalism was used. Since basis sets for dysprosium were not available at the time in the package, Dy(iii) ions were substituted by La(iii) ions. Double-ζ polarized basis sets (mid-PBE for La, DZVP-MOLOPT-SR47 for other atoms) with Goedecker–Teter–Hutter norm conserving pseudopotentials were employed. The PW cutoff was set to 400 Ry.

Calculations to estimate the excited state energies and magnetic anisotropy were performed with the package of programs MOLCAS 8.1.72 The active space consisted of nine electrons in the seven 4f orbitals of the lanthanide ion, i.e. CASSCF(9,7).73,74 All-electron ANO-RCC75–77 basis sets were employed in all the calculations (see Table S1† for details and contraction schemes). State-average calculations were performed only considering all the sextets (21 roots). The Complete Active Space State Interaction (CASSI-SO) was calculated, using the previously computed CASSCF states to check the effect of the spin–orbit splitting on the 6H15/2 ground state. Only the sextets (6H, 6F, and 6P sextets) were taken into consideration since the inclusion of other multiplets did not improve the solution.2,38 Moreover, we chose not to include a second order perturbation on top of the CAS solution (CASPT2) since the effect on energy of the first two excited Kramers' doublets was of the order of only a few wavenumbers.2

The main magnetic axes for the first eight Kramers' doublets were computed with the SINGLE-ANISO module78 with pseudospin S = 1/2. γ0 and γ1 correspond to the angles between the experimental magnetic easy axis and the computed one for the ground and the first excited Kramers' doublets, respectively (Fig. 1).

The atomic electric multipole moments were computed with the LOPROP module79 on the ground state electronic density obtained with the CASSCF/CASSI-SO method. The highly reliable80 LOPROP electrostatic charges, dipoles and quadrupoles computed for all the atoms in the DyDOTA models were employed as a basis for the analysis of the electrostatic field around the Ln ion, performed with the homemade CAMMEL (CAlculated Molecular Multipolar ELectrostatics) code.81–83

Rigid rotation of the two optimized HAWM atoms along the Dy-OAWM axis defines an angle α, whose original value of 0° corresponds to the optimized HAWM positions and it can vary from 0 to 2π values (Fig. 1). For M1 and M2, α was varied along the whole [0, 2π] range. For M3, M4, and M5, calculations were performed only for α = 0° and 90°. The φ angle has been set to the following values: 0°, 53.6°, and 90° (see Fig. 1).

Results and discussion

Rotation of the ground state's easy axis of magnetization

The results obtained for all models for angles α = 0° and 90°, and with no AWM, are reported in Table 2 (see also Tables S2 and S3†). The observed behaviour immediately appears to be strongly model dependent. For M1 (reference model), the computed g-values for α = 0° show a very good agreement between the experimental and the computed easy axis of magnetization orientations (Fig. 3 and 4, and Tables S2 and S3†). The deviation of 3° is well below the experimental uncertainty. However, the role of the AWM seems not to be innocent at all.

Table 2. Orientation of ground Kramers' doublets' main magnetic axis in the molecular frame for the different structural models considered in this paper (M1–5) and for the already published ones.

Model Cucinotta a et al.2 (Mod. A) Cucinotta b et al.2 (Mod. A) Chilton et al.47 M1 M2 M3 M4 M5
α = 0° graphic file with name c9sc01743g-u6.jpg graphic file with name c9sc01743g-u7.jpg graphic file with name c9sc01743g-u8.jpg graphic file with name c9sc01743g-u9.jpg graphic file with name c9sc01743g-u10.jpg graphic file with name c9sc01743g-u11.jpg graphic file with name c9sc01743g-u12.jpg graphic file with name c9sc01743g-u13.jpg
γ 0 9.6° 0.6° ∼0° c 2.8° 8° 5.5° 88° 4.6°
α = 90° graphic file with name c9sc01743g-u14.jpg graphic file with name c9sc01743g-u15.jpg graphic file with name c9sc01743g-u16.jpg graphic file with name c9sc01743g-u17.jpg graphic file with name c9sc01743g-u18.jpg graphic file with name c9sc01743g-u19.jpg graphic file with name c9sc01743g-u20.jpg graphic file with name c9sc01743g-u21.jpg
γ 0 85.8° 41.0° ∼0° c 34.1° 81.1° 3.5° 84° 11.9°
No H2O graphic file with name c9sc01743g-u22.jpg graphic file with name c9sc01743g-u23.jpg graphic file with name c9sc01743g-u24.jpg
γ 0 7.6° 3.0° 77.5°
Open in a new tab

aExact Model A in Cucinotta et al.2 (φ = 0°).

bModified Model A in Cucinotta et al.2 (φ = 53.6°).

cExtracted values from Fig. 3 of Chilton et al.47 (exact values were not reported).

Fig. 3. Model M1. Computed ground state easy axis for different α angles inside the molecular frame.

Fig. 3

Open in a new tab

Fig. 4. Model M1. Variation of the angle γ0,1 as a function of the rotation of the AWM (α), for ground and first excited states.

Fig. 4

Open in a new tab

Indeed, for α = 90°, the easy axis of magnetization remains in the plane containing the DOTA oxygen atoms coordinating the Dy(iii) ion but the value of γ0 is now 34.1° and reaches a maximum of 71.7° (Fig. 3 and 4) for α = 120°. The obtained results show a similar trend with respect to the ones obtained by Cucinotta et al.2 However, in the latter work, they found the maximal extent of the rotation of the easy axis of magnetization (γ0 = 85.8°) for α = 90°. Puzzled by these differences, we changed the φ value in Cucinotta et al.'s model from 0° to the optimized one (53.6°), as previously stated in the Computational details: the γ0 values for α = 0° and 90° changed to 0.6° and 41°, respectively, in very good agreement with M1 findings. These results also evidenced how significant the effects derived from a different geometrical modeling of the AWM can be on the description of the magnetic properties of the system. Moreover, different from what was calculated by Cucinotta et al.,2 by removing the water molecule we observed a γ0 angle of only 3°.

A completely different approach from M1 is represented by the choice of M2. Indeed, this model represents, along with M2m (see the ESI†), the simplest possible model and the most common approach used in the literature for lanthanide-based SMMs, at the same time.29,39,63 A similar trend to the one observed for M1 was found. The main difference lies in the maximal extent of the rotation of γ0 and the value of α at which it is obtained: 81.1° vs. 71.7° (M1) and 90° vs. 120° (M1), respectively. The effect of the removal of the AWM has also been studied for this model. In this case, the easy axis of magnetization shows a γ0 angle of 77.5°, in agreement with the article by Cucinotta et al.2

The results obtained for M3 are in agreement with the ones reported by Chilton et al.47: no reorientation of the easy axis of magnetization was observed (γ0 = 5.5° and 3.5° for α = 0° and 90°, respectively). This result, compared to the ones obtained for M1 and M2, gives a strong indication of how sensitive to the modeling of its electrostatic environment the Dy(iii) ion can be. In this framework, the M3 model shows a possible bias constituted by the arbitrariness of having three Na+ ions with their coordination sphere unsaturated.

To overcome such a bias, M4 was built to have the Na+ ions fully coordinated (see the Computational approach and ESI†). The non-innocence of such a change in the modeling is witnessed by the results reported in Tables 2 and S2.† Indeed, the easy axis of magnetization was found at γ0 values of 88° and 84° for α = 0° and 90°, respectively. This means that the addition of formate ions and water molecules has strong effects on the fine magnetic structure of the system, even if they belong only to the second and third coordination spheres of the Dy(iii) ion. Such results show, once again, how sensitive the Dy(iii) ion can be to the modelling of its electrostatic environment. No reorientation of the easy axis of magnetization, but now with small γ0 values, was also found for M5, which is very close to the findings for the Model A/A′ proposed by Cucinotta et al.2 Despite the close similarity, γ0 values of 4.6° and 11.9° (Tables 2 and S2†) were found for α = 0° and 90°, respectively. Instead, a change of orientation of the easy axis of magnetization of about 90° was found for Model A/A′ passing from α = 0° to α = 90°. This result confirms once again the strong modeling effects on the fine electronic structure of the Dy(iii) ion when partial, not to mention “arbitrary”, models are chosen.

AWM's influence on the energy ladder

Given for granted the role of the AWM in the modulation of the magnetic properties of DyDOTA, we wanted to shed more light on it, also from the perspective of the more ambitious aim of quantifying the covalent contributions in the Dy-OAWM bond (see the next section). We, therefore, monitored the evolution of the electronic structure of M1 for twenty values of the α angle. The principal g-values of the ground and first excited Kramers' doublets and the angle between the computed gz components and the experimental value are reported in Table S4† and Fig. 3 and 4, respectively.

The computed g-values for α = 0° show a stronger Ising character of the Dy(iii) ion than the one experimentally observed but in agreement with the previously computed g-values by Cucinotta et al. (Table S4†) and the usual trend reported in the literature.39,42,80

The ground and the first excited Kramers' doublets show a prominent contribution from the |Mj〉 = 15/2 and | = 15/2 and |Mj〉 = 13/2 components (ESI and Tables S5 and S6 = 13/2 components (ESI and Tables S5 and S6†) and they are separated by 47 cm–1, in excellent agreement with an experimental value of 52 cm–1. A very good agreement is also evidenced for higher energy doublets which differ from the experimental ones of 16 cm–1 at maximum. Only for E2 and E5, a more significant deviance from the luminescence experimental values2 was found: deviations of 28 and 31 cm–1, respectively (Table S4†).

The overall agreement with the experiment is evident. This is not surprising since the present computational model represents so far the most accurate representation of the environment that a single [Dy(DOTA)(H2O)]– unit can experience. In a nutshell, the geometrical and chemical arbitrariness were reduced to the minimum in this model.

Interestingly, the first excited Kramers' doublet also shows a significant Ising character and the orientation of its gz component is quasi-orthogonal (80.1°) to the one of the ground doublet.

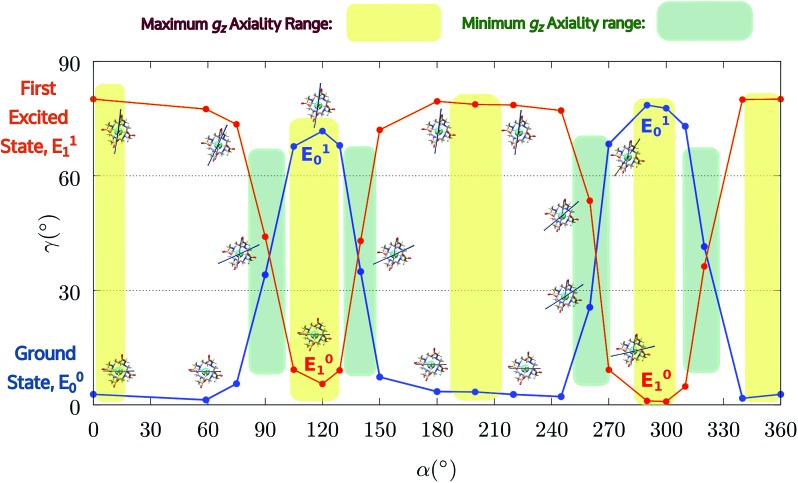
Encouraged by these results, we performed the same calculations for different α values. First of all, we tried to calculate the evolution of the orientation of the easy axis of magnetization for 0° < α < 90° as already reported in the literature2,47 (Fig. 3 and 4 and Table S4†) and then extended it to 90° < α < 360°. The choice to extend the α range is due to the asymmetry introduced by the presence of the two carboxylate groups coordinating the HAWM atoms in the explicit [Dy(DOTA) (H2O)]– unit. For more clarity, the gz orientations as a function of the α angle are collected for both the ground and the first excited Kramers' doublet in Fig. 3 and 4. Regarding the ground state (blue curve in Fig. 4), the value of γ0 remains almost constant up to α = 60° and only beyond this value does it increase up to its maximum value of γ0 = 71.7° computed for α = 120°. Therefore, the easy axis orientation change can be considered as a smooth process since a range of 60° is needed by the angle α to cover the gap between the minimum and maximum γ0 values. Moreover, the easy magnetization axis took about 60° (α = 180°) to recover a value of γ0 close to 0°.

A similar trend is also observed for 180° < α < 360°, even if a slightly higher maximum was achieved (γ0 = 78.5°), maintaining practically unaltered the range of α values for which the variation of γ0 takes place.

These results are important for two main reasons: first, they show that a strong reorientation of the easy axis of magnetization can be induced by the simple rotation of the AWM but at larger values than α = 90°, in contrast to what was reported for previous models.2,47 Secondly, the reorientation is a smooth phenomenon and not an abrupt one as reported in Cucinotta et al.,2 where the change in the orientation of γ0 was observed within 15° of the α angle: γ0 passed from ∼1° to 92° from α = 45° to α = 60°. However, by only changing φ to the Cucinotta et al. value, we can recover the abrupt switch between E0 and E1 doublets.

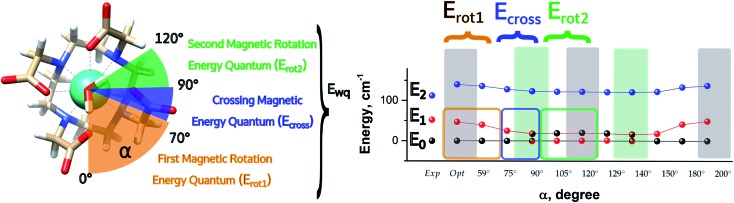
It is also worth stressing that similar results, but opposite in trend, were obtained for the first excited Kramers' doublet. Interestingly, the sum of the two γ0,1 values observed for the ground and the first Kramers' doublet state, respectively, is found to be constant (80° ± 3°) for the entire 2π range. On this basis, we can theorize that E0 goes toward a swapping process with E1 depending on the rotation angle of the water molecule. From an accurate analysis of the energy ladders calculated for different α angle values, such a flipping process between the two first Kramers' doublets can be rationalized in three main steps (Fig. 5).

Fig. 5. Energetic variations involving the ground and first excited Kramers' doublet as a function of the AWM's angle of rotation α for M1.

Fig. 5

Open in a new tab

In the first step, where α values range between 0° and 70°, the rotation of the water molecule alone induces a destabilization of E0 of about 20–25 cm–1 (Erot1), leaving the energy ladder practically unchanged for E2–E7 (a rigid stabilizing shift of 20 ± 3 cm–1 is observed, see Table S4†). In contrast, the energy of the first excited Kramers' doublet, E1, remains practically constant. In this α range, both E0 and E1 retain their original easy magnetic axis orientation (2.8° < γ0 < 5.5° and 73.5° < γ1 < 80.1°).

In the second step, that is for 70° < α < 90°, we observed a kind of avoided crossing scenario between the E0 and E1 states. This is witnessed by the fact that for α = 90° we have an intermediate easy axis orientation both for the ground and the first excited Kramer's doublet (γ0 = 34.1° and γ1 = 44.0°, respectively). Indeed, from the analysis of their composition for this α angle emerged that they have a very similar composition (Tables S5 and S6†), confirming that the energy surfaces for E0 and E1 undergo to an avoided crossing process. We can qualitatively estimate Ecross ∼20 cm–1.84

In the third step, where α values range between 90° and 120°, the energies involved are the ones needed to re-flip the two Kramers' doublet states and make their compositions similar to their original ones with their easy axes of magnetization quasi-orthogonal again (67.7° < γ0 < 71.7°, 9.2° < γ1 < 5.5°). In this regard, it is not surprising that an Erot2 value equal to the one obtained for 0° < α < 70° is found. From the considerations above, we can say that the energy quantum involved in reaching the avoided crossing point (Erot1 + Ecross) is about 40–50 cm–1. The energy needed to completely rotate the easy magnetization axis (Erot1 + Ecross + Erot2) can be, therefore, estimated to be about 60–70 cm–1. This result suggests that in the case where the separation energy between the first two Kramers' doublets would exceed the required flip energy quantum (40–50 cm–1), reorientation of the easy axis of magnetization would not likely take place. Of course, the value of the energy flip quantum could be model dependent, but the physics under the phenomenon is valid in general (vide infra). Unexpectedly, in the 90° < α < 140° range, corresponding to the flip of the easy axis of magnetization from γ0 ∼ 0° to 72° and back to 35°, the E0–E7 energies show very small variations (1–3 cm–1). This can be explained by the fact that the two doublets are not completely flipped, except for α = 120°. From α = 150°, a new flip between the first two doublets was observed, leading to values of γ0 and doublet ladder energies for α = 200°, which correspond to the ones computed for α = 0° (Table S4†). From this α value, the ground doublet energy started to destabilize again by the further AWM rotation until when, for α = 260°, a further flip of the easy axis of magnetization was computed. In the range 270° < α < 320°, E0–E7 energies were computed very close to the corresponding energies found for the 90° < α < 140° range.

From the present results, the pivotal importance of periodic contributions clearly emerges, even if they are treated only at an electrostatic level and with an indirect inclusion. Their introduction revealed, indeed, a richer electronic structure than the one observed in simpler models. The analysis done so far can give a hint as to the reason why different models in the literature did not show any changes in the orientation of the easy axis of magnetization as a function of α: all depends on the computed deviation from the experimental E0–E1 gap. Indeed, since the rotation of the AWM requires an energy of about 60–65 cm–1 going from α = 0° to α = 120°, in the case where the computed gap is larger than 60–70 cm–1, no flip of the easy axis will likely be observed (see Chilton et al.47); in the case where the gap is smaller, the ground doublet can be erroneously computed due to a poor geometrical modeling choice, thus leading to a partial or total prevalence of a wrong orientation of the easy axis of magnetization (M3–5). It becomes evident that the modeling of lanthanide systems needs considerable care to avoid unwanted misinterpretation of the experimental findings.

The effect on the energy ladder due to the removal of the AWM was also studied. Focusing on the energy values of the ground and the first excited Kramers' doublets, a shift of the latter by 20 cm–1 was observed (see Table S3†).

With the aim of verifying the influence of the model on the electronic and magnetic structure, we studied M2 (and the M2m model derived from it) at the same extent as for M1, calculating the evolution of the electronic structure for eighteen values of α (Tables S7 and S8, and Fig. S7–S9†). Despite an apparent similarity to M1, slight but important differences in the electronic structure can be noted. In agreement with M1, the rotation effect on the flip of the easy axis is fully confirmed as its Ising type along all the α values, even if the rhombicity is more enhanced than in M1 and, therefore, there is even better agreement with the experiment. The deviation of 8° from the experimental orientation of the gz values is below experimental uncertainty.

As for M1, the ground and the first excited Kramers' doublets show a prominent contribution from |Mj〉 = 15/2 and | = 15/2 and |Mj〉 = 13/2, but in this case, they are separated by only 15 cm = 13/2, but in this case, they are separated by only 15 cm–1versus an experimental value of 53 cm–1. In this case, (Erot1 + Ecross) is ∼40 cm–1, in good agreement with the value found in the M1 model. The maximum flip is now reached in a narrower α range (0° < α < 90°) and the flip can happen at lower α values (45°) than in M1 because in this case Erot1 and E0–E1 are comparable. Even for this model the two γ0,1 values are nearly complementary (77° ± 13°) as observed in M1 for all α values. The effect of φ on the first four excited Kramers' doublets is limited to tens of cm–1 (see Tables S9 and S10†).

The effect of the removal of the water molecule has also been studied for this model (Table S3†). The energy separation between the ground and the first excited Kramers' doublets is equivalent to the one found for M1 without the AWM. However, in this case, the easy axis of magnetization showed a γ0 value of 77.5°, in agreement with Cucinotta et al.2 This result further stresses the model dependency of magnetic properties.

Based on the above analysis, it becomes straightforward to rationalize the different computed effects of the AWM on the easy axis orientation in the other models and in the ones already reported in the literature. Indeed, the absence of easy axis rotation in M3 can now be explained by the computed large E0–E1 separation with respect to the (Erot1 + Ecross) quantum involved in the AWM rotation, preventing, de facto, the flip between the two states for the entire range of α values, 90° included.

In the case of M4, we have instead a situation where the ground state is flipped with the first excited one for all the α angle values. This means that the inclusion of the formate ions and the water molecules in the second and third coordination spheres of the Dy(iii) ion is not negligible at all because it strongly stabilizes the Kramers' doublet characterized by a perpendicular orientation of the easy axis with respect to the experimental one becoming the ground state even for α = 0°. In M5 the effect of the model choice (inclusion of point charges) is opposite and it always stabilizes the doublet characterized by a close orientation of the easy axis to the experimental one.

Analyzing the computed energy values for the first eight multiplets of M3–5 models (Table S2†), several important pieces of information can be extracted (for a more detailed discussion see the ESI†). First of all, comparing the computed trends for the ground and the first excited Kramers' doublets for the three models, it is found that the rotation of the AWM has opposite effects on them, strongly destabilizing the former and slightly stabilizing the latter. Moreover, the energy required for the AWM rotation in the range 0° < α < 90°, i.e. (Erot1 + Ecross), is consistently found to be 40 ± 3 cm–1 for all the models.

About the nature of the Dy-OAWM bond

Focusing on the nature of the coordinative bond in lanthanide complexes, the periodic computed trend of the variation of the doublet energy ladder as a function of the α value suggested that the interaction between the Dy(iii) ion and the water molecule could hide a more complex “courtship ritual” than the expected one given by simple electrostatic interactions. For these reasons, we performed a series of further calculations aimed at shedding light on this appealing topic.

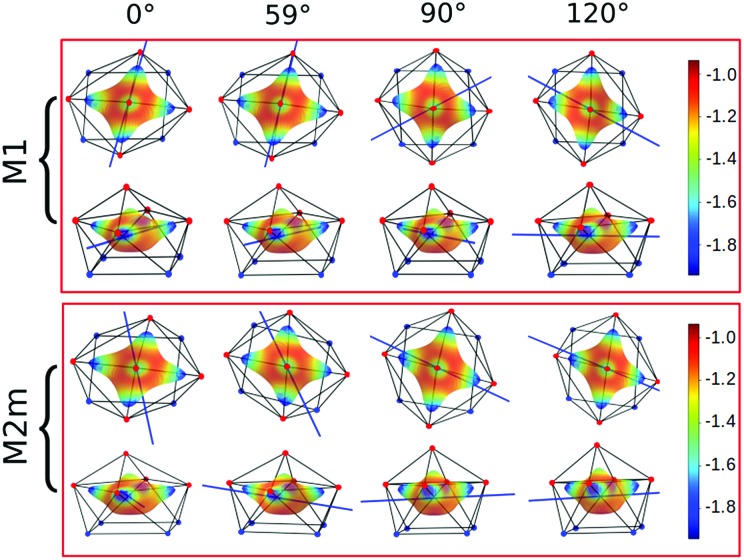
The common assumption is that electrostatic interactions, due to the inner nature of f orbitals, are the main interactions responsible for the ligand field effects in lanthanide containing complexes and, therefore, their magnetic properties are strongly dependent on them. Thus, we performed a multipolar electrostatic analysis of M1 and M2m through which it was possible to access the single charge, dipolar and quadrupolar contributions to the electrostatic potential. This analysis was performed using the CAMMEL code for four α values (0°, 59°, 90°and 120°). We chose these two models, i.e. the most accurate one versus the simplest one, to have clearer indications without any loss of generality.

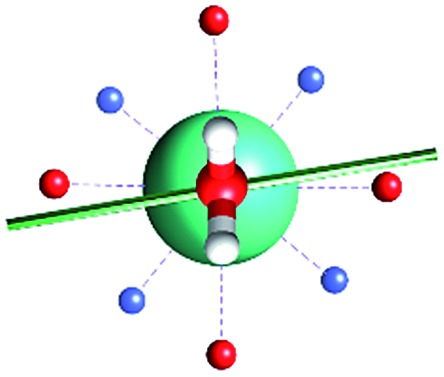
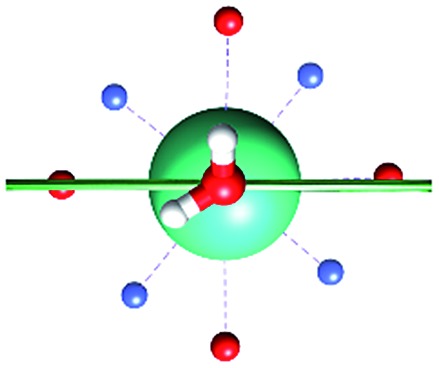
The results of the CAMMEL analysis for both models are reported in Fig. 6 and S10–S17.† They indicate the presence of four minima in the whole electrostatic potential which point toward the four coordinating carboxylic oxygen atoms. From the multipolar decomposition, it is possible to ascribe the presence of minima to the dipolar and quadrupolar components, while the contribution generated by the charges shows, instead, a more isotropic shape. Such a scenario does not show any appreciable differences for both considered models and the corresponding α sets of values. This clearly indicates that the electrostatic environments show two equivalent preferential orientations for the easy axis of magnetization, which qualitatively correspond to the computed directions of the first two doublets. However, the analysis cannot give any indication as to which of the two directions can be the one associated with the ground doublet.

Fig. 6. Electrostatic potential computed by CAMMEL for M1 and M2m at different α angles. For each α angle, the top and side views of the complex are shown. Only the atoms directly bonded to the Dy(iii) ion are showed. Oxygen and nitrogen atoms are red and blue, respectively. The orientation (blue line) of the easy axis of magnetization for each geometry is also shown.

Fig. 6

Open in a new tab

From the analysis of the plots reported in Fig. 6 and S10–S17,† it is not possible to gain any evident information regarding the subtle role of the AWM. In this regard, we tried to extrapolate the single electrostatic contributions of the AWM by plotting the difference between the potentials calculated for M1 and its counterpart without the AWM for the two sets of α values. In both cases, we can observe that the quadrupolar potential represents the strongest electrostatic contribution as expected for a water molecule85 (Fig. S18†), but a variation of the potential as a function of the α values is observed only for the dipolar component. To verify if eventual variations in the quadrupolar potentials could be hidden by isotropic contributions, we also re-plotted the map differences, subtracting the AWM potential previously obtained for α = 0° as the reference (Fig. S19†). The new plots evidenced a variation in the potential also for the quadrupolar contribution and this variation is of the same order of magnitude as that of the dipolar component. In a nutshell, we can expect that the electric quadrupolar field of the water molecule should play a major role in the re-orientation mechanism of the easy axis of magnetization while a minor role is expected for the dipole. In the case of the charge, we can exclude any significant role in it.

Strong in the results obtained, we tried to justify them through a more accurate computational approach. With this aim, we performed CASSCF/CASSI-SO calculations for M1 for the same 0°–90°–120° set of α values, substituting the AWM atoms with their multipolar expansion (M1#). With such a “trick” we can access the whole and the single electrostatic contributions and readily verify their effects on the energy ladder and, consequently, on the orientation of the easy axis of magnetization. The results are reported in Table S11.† The results obtained for M1# indicate that the whole electrostatic contribution coming from the AWM is able to rotate the easy axis but not completely (γ0 = 46.3°), as found when the AWM is explicitly considered (γ0 = 71.7°). Comparing the E0 and E1 values for α = 0° and 120° it is then possible to assign a new easy axis energy quantum of ∼65 cm–1 (E#rot1 + E#cross). Such an energy value can therefore explain the computed intermediate γ0 value since the starting E1 is at 58 cm–1, which is too high in energy to observe a complete flip. Interestingly, the computed (E#rot + E#cross) energy for M1# is the same as the energy previously found in the M1 model for Erot1 + Ecross + Erot2.

The expressions for the two energies describe, indeed, the same process; the only difference is that while for the former a total localization of the state is possible (E1,α=0° < 50 cm–1), for the latter the localization is not possible because E1,α=0° > 50 cm–1. This result is important because it demonstrates that the rotation of the easy axis is in large part driven by an electrostatic constant energy quantum. At the same time, the cruciality of having an accurate description of the energy ladder must be stressed once again. This is possible only when covalent contributions are included and a reliable environment is modeled, too. The fingerprint of covalent contributions can be hinted at by looking at the magnetic easy axis computed for α = 0°, where, indeed, a difference in γ0 of 4° was found. On the other hand, the difference in the energy ladders is significant.

Based on these pieces of evidence, we also eventually investigated the different roles of the electrostatic potential using M1#. The results are reported in Table S12.† In agreement with the pure electrostatic approach, the driving force of the easy axis rotation is mainly due to the quadrupolar (80%, γ0 = 36.2°) and point charge electrostatic field (15% γ0 = 6.5°) while the dipole moment has only a minor effect. In this regard, to support the previous clues, we performed CASSCF/CASSI-SO calculations for M1 and M1# for α = 120°, where we stretched the Dy-OAWM bond for a maximum of 0.2 Å, as reported in Table 3. The choice of α = 120° is justified by the fact that the removal (i.e. extreme stretching situation) of the water molecule in M1 results in γ0 = 4°. Therefore, stretching the Dy-OAWM for α = 120° geometry we can get further hints about the nature of the bonding and the factors ruling the rotation of the easy axis.

Table 3. Results of the calculations on model M1, as a function of the Dy-OAWM stretching (in Angstrom) for α = 120°. Results obtained by substituting the AWM with its multipole expansion were also reported.

Exp 0 Å
 0.05 Å
 0.1 Å
 0.15 Å
 0.2 Å
 No H2O
Orb Charges Orb Charges Orb Charges Orb Charges Orb Charges
Principal g-values of the ground Kramers' doublet
g x 3.4 0.9 0.5 0.9 0.6 1.0 0.7 1.0 0.7 1.0 0.7 0.6
g y 4.9 4.1 1.8 5.0 3.5 5.8 3.9 6.5 4.0 6.9 3.8 2.9
g z 17.0 16.0 14.6 15.1 14.6 14.3 15.0 13.7 15.4 13.3 15.8 17.3
 
γ 0 angle between experimental and calculated g z
71.7° 46.3° 67.7° 29.1° 62.0° 19.2° 54.2° 14.2° 44.7° 11.2° 3.0°
 
Energy levels (cm –1 )
E0 0 0 0 0 0 0 0 0 0 0 0 0
E1 52 20 6 18 7 17 8 16 10 16 11 27
E2 112 122 97 122 101 123 106 123 109 124 112 146
E3 198 194 144 193 152 193 159 193 166 194 171 231
E4 287 281 229 283 239 285 249 288 257 291 265 356
E5 400 351 298 359 316 367 332 376 346 384 359 506
E6 454 430 378 448 405 465 431 482 453 499 473 702
E7 574 566 470 595 515 622 557 648 593 673 625 982
Open in a new tab

Focusing on the energy trends of E0 and E1, we can observe that when the orbital contributions for the AWM are included, the E1 values became stabilized as the Dy-OAWM bond was stretched. This is an expected behavior since the system tends toward a situation where the AWM is absent, and, therefore, to a situation where E1 flips with E0 in the range 70°< α < 90°.

Associated with the E1 stabilization, we can also observe a decrease of the γ0 values. An opposite situation is found for M1#: in this case E1 energies become destabilized as the Dy-OAWM bond is stretched. This result indicates that in M1# for α = 120°, E0 and E1 are already flipped. For this reason, we can observe a similar trend of E1 destabilization to that in M1 but associated with a sudden γ0 decrease, while in M1 a smoother decrease (overlap vs. coulomb interaction) was found.

In the light of the previous clues, considering that in M1# for α = 120°, E0 and E1 are already flipped, we can reconsider the nature of the (E#rot1 + E#cross) energy quantum. Indeed, comparing the E0–E1 energy splitting (20 and 6 cm–1 for M1 and M1#, respectively) obtained for α = 0°, we can now confidently say that the energy quantum of AWM rotation can be divided into ∼50 cm–1 (75%) coming from an electrostatic contribution and ∼15 cm–1 (25%) from an orbital contribution. This value is also compatible with the difference of few degrees computed for M1 and M1# at α = 0°. Such results undoubtedly indicate that the covalent contribution is much more relevant than estimated before for Ln-halide bonds and, consequently, that the orientation of the easy axis is the result of the complex balancing between electrostatic and covalent contributions.53,56

Conclusions

We have performed exhaustive state-of-the-art computational analysis of the role of the AWM in tuning the magnetic properties in a very actual compound, as DyDOTA is, both because of its archetypal role in molecular magnetism and its application as an MRI contrast agent. The proposed approach and the conclusions presented herein can be extended, in general, to other lanthanide based14 complexes and even beyond the solid state, including MRI relaxation mechanisms in solution.

Our study allowed us to rationalize the different outcomes of previous studies presented in the literature, demonstrating that DyDOTA's behaviour is unique and depends on the correct representation of the crystallographic environment (i.e. Madelung potential) and the AWM itself. Once they are correctly represented in the in silico experiment, we showed that the rotation of the AWM effectively strongly influences the orientation of the easy axis of magnetization for a maximum value of 70° with a smooth process. Moreover, we demonstrated that the rotation of the easy axis is due to the flipping of the ground doublet with the first excited one. Therefore, the accurate calculation of this gap, Δ(E1 – E0), becomes mandatory. In this regard, we were also able to quantify the energy flip quantum, Ewq, as ∼65 cm–1. Consequently, only in the case where the Δ(E1 – E0) is smaller than the Ewq, the two first doublets can flip and the orientation of the easy axis with them.

Such deep analysis also gave us the opportunity to obtain unprecedented information about the nature of the Dy-OAWM bond. Indeed, through electric multipolar expansion analysis and ab initio magneto-structural correlations, we reached the conclusions that electrostatic contributions are not enough to explain the rotation of the easy axis and that the quadrupolar potential is its main driving force. And last but not least, we showed that a clear and crucial covalent footprint is present and it can be quantified as the ∼25% of the Dy-OAWM bond.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

Click here for additional data file. (10.3MB, pdf)

Acknowledgments

We acknowledge the financial contribution of the ERC through the AdG MolNanoMas (267746). B. L. G. thanks the French GENCI/IDRIS-CINES center for high-performance computing resources. We are thankful for the financial support of the Brazilian agency Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ).

Footnotes

†Electronic supplementary information (ESI) available: Description of the employed geometrical models and employed ANO-RCC basis sets and contractions; results of the CASSCF-CASSI-SO calculations for all the α and φ angles in all the models (g-tensors of the ground and first excited doublets, γn angles, energy ladder of the ground J = 15/2 multiplet); and electrostatic potential maps by CAMMEL for M1 and M2m. See DOI: 10.1039/c9sc01743g

References

  1. Caravan P., Ellison J. J., McMurry T. J., Lauffer R. B. Chem. Rev. 1999;99:2293–2352. doi: 10.1021/cr980440x. [DOI] [PubMed] [Google Scholar]
  2. Cucinotta G., Perfetti M., Luzon J., Etienne M., Car P. E., Caneschi A., Calvez G., Bernot K., Sessoli R. Angew. Chem., Int. Ed. 2012;51:1606–1610. doi: 10.1002/anie.201107453. [DOI] [PubMed] [Google Scholar]
  3. Boulon M.-E., Cucinotta G., Luzon J., Degl'Innocenti C., Perfetti M., Bernot K., Calvez G., Caneschi A., Sessoli R. Angew. Chem., Int. Ed. 2013;52:350–354. doi: 10.1002/anie.201205938. [DOI] [PubMed] [Google Scholar]
  4. Car P.-E., Perfetti M., Mannini M., Favre A., Caneschi A., Sessoli R. Chem. Commun. 2011;47:3751–3753. doi: 10.1039/c0cc05850e. [DOI] [PubMed] [Google Scholar]
  5. Desreux J. F. Inorg. Chem. 1980;19:1319–1324. [Google Scholar]
  6. Kumar K., Chang C. A., Francesconi L. C., Dischino D. D., Malley M. F., Gougoutas J. Z., Tweedle M. F. Inorg. Chem. 1994;33:3567–3575. [Google Scholar]
  7. Aime S., Barge A., Botta M., Parker D., De Sousa A. S. J. Am. Chem. Soc. 1997;119:4767–4768. [Google Scholar]
  8. Blackburn O. A., Chilton N. F., Keller K., Tait C. E., Myers W. K., McInnes E. J. L., Kenwright A. M., Beer P. D., Timmel C. R., Faulkner S. Angew. Chem., Int. Ed. 2015;54:10783–10786. doi: 10.1002/anie.201503421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Micskei K., Helm L., Brucher E., Merbach A. E. Inorg. Chem. 1993;32:3844–3850. [Google Scholar]
  10. Soesbe T. C., Ratnakar S. J., Milne M., Zhang S., Do Q. N., Kovacs Z., Sherry A. D. Magn. Reson. Med. 2014;71:1179–1185. doi: 10.1002/mrm.25091. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Zheng X. Y., Pellico J., Khrapitchev A. A., Sibson N. R., Davis J. J. Nanoscale. 2018;10:21041–21045. doi: 10.1039/c8nr07198e. [DOI] [PubMed] [Google Scholar]
  12. Viswanathan S., Kovacs Z., Green K. N., Ratnakar S. J., Sherry A. D. Chem. Rev. 2010;110:2960–3018. doi: 10.1021/cr900284a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Graham B., Loh C. T., Swarbrick J. D., Ung P., Shin J., Yagi H., Jia X., Chhabra S., Barlow N., Pintacuda G., Huber T., Otting G. Bioconjugate Chem. 2011;22:2118–2125. doi: 10.1021/bc200353c. [DOI] [PubMed] [Google Scholar]
  14. Benda L., Mares J., Ravera E., Parigi G., Luchinat C., Kaupp M., Vaara J. Angew. Chem., Int. Ed. 2016;55:14713–14717. doi: 10.1002/anie.201608829. [DOI] [PubMed] [Google Scholar]
  15. Dasgupta S., Hu X., Keizers P. H. J., Liu W. M., Luchinat C., Nagulapalli M., Overhand M., Parigi G., Sgheri L., Ubbink M. J. Biomol. NMR. 2011;51:253–263. doi: 10.1007/s10858-011-9532-2. [DOI] [PubMed] [Google Scholar]
  16. (a) Liddle S. T., van Slageren J. Chem. Soc. Rev. 2015;44:6655–6669. doi: 10.1039/c5cs00222b. [DOI] [PubMed] [Google Scholar]; (b) Zhang P., Zhang L., Tang J. Dalton Trans. 2015;44:3923–3929. doi: 10.1039/c4dt03329a. [DOI] [PubMed] [Google Scholar]; (c) Zhu Z., Guo M., Li X.-L., Tang J. Coord. Chem. Rev. 2019;378:350–364. [Google Scholar]; (d) Zhang P., Zhang L., Wang C., Xue S., Lin S.-Y., Tang J. J. Am. Chem. Soc. 2014;136:4484–4487. doi: 10.1021/ja500793x. [DOI] [PubMed] [Google Scholar]
  17. Gatteschi D., Sessoli R. and Villain J., Molecular Nanomagnets, OUP, Oxford, 2011. [Google Scholar]
  18. Mannini M., Pineider F., Sainctavit P., Danieli C., Otero E., Sciancalepore C., Talarico A. M., Arrio M., Cornia A., Gatteschi D., Sessoli R. Nat. Mater. 2009;8:194–197. doi: 10.1038/nmat2374. [DOI] [PubMed] [Google Scholar]
  19. Mannini M., Pineider F., Danieli C., Totti F., Sorace L., Sainctavit P., Arrio M., Otero E., Joly L., Cezar J. C., Cornia A., Sessoli R. Nature. 2010;468:417–421. doi: 10.1038/nature09478. [DOI] [PubMed] [Google Scholar]
  20. Kalff F. E., Rebergen M. P., Fahrenfort E., Girovsky J., Toskovic R., Lado J. L., Fernández-Rossier J., Otte A. F. Nat. Nanotechnol. 2016;18:926–929. doi: 10.1038/nnano.2016.131. [DOI] [PubMed] [Google Scholar]
  21. Aguila D., Barrios L. A., Velasco V., Roubeau O., Repolles A., Alonso P. J., Sese J., Teat S. J., Luis F., Aromi G., Pablo J. J. Am. Chem. Soc. 2014:14215–14222. doi: 10.1021/ja507809w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Shiddiq M., Komijani D., Duan Y., Gaita-Ariño A., Coronado E., Hill S. Nature. 2016;531:348–351. doi: 10.1038/nature16984. [DOI] [PubMed] [Google Scholar]
  23. Sanvito S. Chem. Soc. Rev. 2011;40:3336. doi: 10.1039/c1cs15047b. [DOI] [PubMed] [Google Scholar]
  24. Vincent R., Klyatskaya S., Ruben M., Wernsdorfer W., Balestro F. Nature. 2012;488:357–360. doi: 10.1038/nature11341. [DOI] [PubMed] [Google Scholar]
  25. Ganzhorn M., Klyatskaya S., Ruben M., Wernsdorfer W. Nat. Nanotechnol. 2013;8:165–169. doi: 10.1038/nnano.2012.258. [DOI] [PubMed] [Google Scholar]
  26. Ishikawa N., Sugita M., Ishikawa T., Koshihara S., Kaizu Y. J. Am. Chem. Soc. 2003;125:8694–8695. doi: 10.1021/ja029629n. [DOI] [PubMed] [Google Scholar]
  27. Lunghi A., Totti F., Sessoli R., Sanvito S. Nat. Commun. 2017;8:14620. doi: 10.1038/ncomms14620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lunghi A., Totti F., Sanvito S., Sessoli R. Chem. Sci. 2017;8:6051–6059. doi: 10.1039/c7sc02832f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Goodwin C. A. P., Ortu F., Reta D., Chilton N. F., Mills D. P. Nature. 2017;548:439–442. doi: 10.1038/nature23447. [DOI] [PubMed] [Google Scholar]
  30. Guo F., Day B. M., Chen Y., Tong M., Mansikkamäki A., Layfield R. A. Science. 2018;362:1400–1403. doi: 10.1126/science.aav0652. [DOI] [PubMed] [Google Scholar]
  31. Bunting P. C., Atanasov M., Damgaard-Møller E., Perfetti M., Crassee I., Orlita M., Overgaard J., van Slageren J., Neese F., Long J. R. Science. 2018;362:eaat7319. doi: 10.1126/science.aat7319. [DOI] [PubMed] [Google Scholar]
  32. Goodwin C. A. P., Ortu F., Reta D., Chilton N. F., Mills D. P. Nat. Publ. Gr. 2017;548:439–442. doi: 10.1038/nature23447. [DOI] [PubMed] [Google Scholar]
  33. Guo F. S., Day B. M., Chen Y. C., Tong M. L., Mansikkamäki A., Layfield R. A. Angew. Chem., Int. Ed. 2017;56:11445–11449. doi: 10.1002/anie.201705426. [DOI] [PubMed] [Google Scholar]
  34. Chilton N. F. Inorg. Chem. 2015;54:2097–2099. doi: 10.1021/acs.inorgchem.5b00089. [DOI] [PubMed] [Google Scholar]
  35. Ungur L., Chibotaru L. F. Phys. Chem. Chem. Phys. 2011;13:20086. doi: 10.1039/c1cp22689d. [DOI] [PubMed] [Google Scholar]
  36. Roos B. O., Malmqvist P.-Å. Phys. Chem. Chem. Phys. 2004;6:2919. [Google Scholar]
  37. Malmqvist P. A., Roos B. O., Schimmelpfennig B. Chem. Phys. Lett. 2002;357:230–240. [Google Scholar]
  38. Bernot K., Luzon J., Bogani L., Etienne M., Sangregorio C., Shanmugam M., Caneschi A., Sessoli R., Gatteschi D. J. Am. Chem. Soc. 2009;131:5573–5579. doi: 10.1021/ja8100038. [DOI] [PubMed] [Google Scholar]
  39. Lucaccini E., Briganti M., Perfetti M., Vendier L., Costes J.-P., Totti F., Sessoli R., Sorace L. Chem.–Eur. J. 2016;22:5552–5562. doi: 10.1002/chem.201505211. [DOI] [PubMed] [Google Scholar]
  40. (a) Rousset E., Piccardo M., Boulon M. E., Gable R. W., Soncini A., Sorace L., Boskovic C. Chem.–Eur. J. 2018;24:14768–14785. doi: 10.1002/chem.201802779. [DOI] [PubMed] [Google Scholar]; (b) Guo Y.-N., Ungur L., Granroth G. E., Powell A. K., Wu C., Nagler S. E., Tang J., Chibotaru L. F., Cui D. Sci. Rep. 2014;4:5471. doi: 10.1038/srep05471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pedersen K. S., Ungur L., Sigrist M., Sundt A., Schau-Magnussen M., Vieru V., Mutka H., Rols S., Weihe H., Waldmann O., Chibotaru L. F., Bendix J., Dreiser J. Chem. Sci. 2014;5:1650–1660. [Google Scholar]
  42. Marx R., Moro F., Dörfel M., Ungur L., Waters M., Jiang S. D., Orlita M., Taylor J., Frey W., Chibotaru L. F., van Slageren J. Chem. Sci. 2014;5:3287. [Google Scholar]
  43. Perfetti M., Sørensen M. A., Hansen U. B., Bamberger H., Lenz S., Hallmen P. P., Fennell T., Simeoni G. G., Arauzo A., Bartolomé J., Bartolomé E., Lefmann K., Weihe H., van Slageren J., Bendix J. Adv. Funct. Mater. 2018;28:1801846. [Google Scholar]
  44. Sørensen M. A., Hansen U. B., Perfetti M., Pedersen K. S., Bartolomé E., Simeoni G. G., Mutka H., Rols S., Jeong M., Zivkovic I., Retuerto M., Arauzo A., Bartolomé J., Piligkos S., Weihe H., Doerrer L. H., Van Slageren J., Rønnow H. M., Lefmann K., Bendix J. Nat. Commun. 2018;9:1292. doi: 10.1038/s41467-018-03706-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Vonci M., Giansiracusa M. J., Van Den Heuvel W., Gable R. W., Moubaraki B., Murray K. S., Yu D., Mole R. A., Soncini A., Boskovic C. Inorg. Chem. 2017;56:378–394. doi: 10.1021/acs.inorgchem.6b02312. [DOI] [PubMed] [Google Scholar]
  46. Dunstan M. A., Mole R. A., Boskovic C. Eur. J. Inorg. Chem. 2019:1090–1105. [Google Scholar]
  47. Chilton N. F., Collison D., McInnes E. J. L., Winpenny R. E. P., Soncini A. Nat. Commun. 2013;4:2551. doi: 10.1038/ncomms3551. [DOI] [PubMed] [Google Scholar]
  48. Baldoví J. J., Cardona-Serra S., Clemente-Juan J. M., Coronado E., Gaita-Ariño A., Palii A. J. Comput. Chem. 2013;34:1961–1967. doi: 10.1002/jcc.23341. [DOI] [PubMed] [Google Scholar]
  49. Ungur L., Chibotaru L. F. Chem.–Eur. J. 2017;23:3708–3718. doi: 10.1002/chem.201605102. [DOI] [PubMed] [Google Scholar]
  50. Cosquer G., Pointillart F., Jung J., Le Guennic B., Golhen S., Cador O., Guyot Y., Brenier A., Maury O., Ouahab L. Eur. J. Inorg. Chem. 2014;2014:69–82. [Google Scholar]
  51. Jung J., Cador O., Bernot K., Pointillart F., Luzon J., Le Guennic B. Beilstein J. Nanotechnol. 2014;5:2267–2274. doi: 10.3762/bjnano.5.236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Singh S. K., Gupta T., Ungur L., Rajaraman G. Chem.–Eur. J. 2015;21:13812–13819. doi: 10.1002/chem.201501330. [DOI] [PubMed] [Google Scholar]
  53. Aravena D., Atanasov M., Neese F. Inorg. Chem. 2016;55:4457–4469. doi: 10.1021/acs.inorgchem.6b00244. [DOI] [PubMed] [Google Scholar]
  54. Rajaraman G., Singh S. K., Pandey B., Velmurugan G. Dalton Trans. 2017;46:11913–11924. doi: 10.1039/c6dt03568j. [DOI] [PubMed] [Google Scholar]
  55. Boulon M.-E., Cucinotta G., Luzon J., Degl'Innocenti C., Perfetti M., Bernot K., Calvez G., Caneschi A., Sessoli R. Angew. Chem., Int. Ed. 2013;52:350–354. doi: 10.1002/anie.201205938. [DOI] [PubMed] [Google Scholar]
  56. Jung J., Atanasov M., Neese F. Inorg. Chem. 2017;56:8802–8816. doi: 10.1021/acs.inorgchem.7b00642. [DOI] [PubMed] [Google Scholar]
  57. (a) Jung J., Le Natur F., Cador O., Pointillart F., Calvez G., Daiguebonne C., Guillou O., Guizouarn T., Le Guennic B., Bernot K. Chem. Commun. 2014;50:13346–13348. doi: 10.1039/c4cc05062b. [DOI] [PubMed] [Google Scholar]; (b) Aravena D., Ruiz E. Inorg. Chem. 2013;52:13770–13778. doi: 10.1021/ic402367c. [DOI] [PubMed] [Google Scholar]
  58. Jung J., Yi X., Huang G., Calvez G., Daiguebonne C., Guillou O., Cador O., Caneschi A., Roisnel T., Le Guennic B., Bernot K. Dalton Trans. 2015;44:18270–18275. doi: 10.1039/c5dt03345d. [DOI] [PubMed] [Google Scholar]
  59. Zhang P., Jung J., Zhang L., Tang J., Le Guennic B. Inorg. Chem. 2016;55:1905–1911. doi: 10.1021/acs.inorgchem.5b02792. [DOI] [PubMed] [Google Scholar]
  60. Vonci M., Mason K., Suturina E. A., Frawley A. T., Worswick S. G., Kuprov I., Parker D., McInnes E. J. L., Chilton N. F. J. Am. Chem. Soc. 2017;139:14166–14172. doi: 10.1021/jacs.7b07094. [DOI] [PubMed] [Google Scholar]
  61. Suturina E. A., Mason K., Geraldes C. F. G. C., Kuprov I., Parker D. Angew. Chem., Int. Ed. 2017;56:12215–12218. doi: 10.1002/anie.201706931. [DOI] [PubMed] [Google Scholar]
  62. Pointillart F., Bernot K., Golhen S., Le Guennic B., Guizouarn T., Ouahab L., Cador O. Angew. Chem., Int. Ed. Engl. 2014:1504–1507. doi: 10.1002/anie.201409887. [DOI] [PubMed] [Google Scholar]
  63. Singh S. K., Gupta T., Rajaraman G. Inorg. Chem. 2014;53:10835–10845. doi: 10.1021/ic500772f. [DOI] [PubMed] [Google Scholar]
  64. Neese F. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012;2:73–78. [Google Scholar]
  65. Stephens P. J., Devlin F. J., Chabalowski C. F., Frisch M. J. J. Phys. Chem. 1994;98:11623–11627. [Google Scholar]
  66. Grimme S., Antony J., Ehrlich S., Krieg H. J. Chem. Phys. 2010;132:0–19. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  67. Pantazis D. a., Neese F. J. Chem. Theory Comput. 2009;5:2229–2238. doi: 10.1021/ct900090f. [DOI] [PubMed] [Google Scholar]
  68. Blöchl P. E. J. Chem. Phys. 1995;103:7422–7428. [Google Scholar]
  69. Adamo C., Barone V. J. Chem. Phys. 1999;110:6158–6170. [Google Scholar]
  70. Hutter J., Iannuzzi M., Schiffmann F., Vandevondele J. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014;4:15–25. [Google Scholar]
  71. Goedecker S., Teter M., Hutter J. Phys. Rev. B: Condens. Matter Mater. Phys. 1996;54:1703–1710. doi: 10.1103/physrevb.54.1703. [DOI] [PubMed] [Google Scholar]
  72. Aquilante F., Autschbach J., Carlson R. K., Chibotaru L. F., Delcey M. G., De Vico L., Galván I. F., Ferré N., Frutos L. M., Gagliardi L., Garavelli M., Giussani A., Hoyer C. E., Li Manni G., Lischka H., Ma D., Malmqvist P. Å., Müller T., Nenov A., Olivucci M., Pedersen T. B., Peng D., Plasser F., Pritchard B., Reiher M., Rivalta I., Schapiro I., Segarra-Martí J., Stenrup M., Truhlar D. G., Ungur L., Valentini A., Vancoillie S., Veryazov V., Vysotskiy V. P., Weingart O., Zapata F., Lindh R. J. Comput. Chem. 2016;37:506–541. doi: 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
  73. Luzon J., Sessoli R. Dalton Trans. 2012;41:13556–13567. doi: 10.1039/c2dt31388j. [DOI] [PubMed] [Google Scholar]
  74. Veryazov V., Malmqvist P. A., Roos B. O. Int. J. Quantum Chem. 2011;111:3329–3338. [Google Scholar]
  75. Roos B. O., Lindh R., Åke Malmqvist P., Veryazov V., Widmark P. O. J. Phys. Chem. A. 2004;108:2851–2858. [Google Scholar]
  76. Veryazov V., Widmark P.-O., Roos B. O. Theor. Chem. Acc. 2004;111:345–351. [Google Scholar]
  77. Roos B. O., Lindh R., Malmqvist P.-A., Veryazov V., Widmark P.-O., Borin A. C. J. Phys. Chem. A. 2008;112:11431–11435. doi: 10.1021/jp803213j. [DOI] [PubMed] [Google Scholar]
  78. Chibotaru L. F., Ungur L. J. Chem. Phys. 2012;137:064112. doi: 10.1063/1.4739763. [DOI] [PubMed] [Google Scholar]
  79. Gagliardi L., Lindh R., Karlstrom G. J. Chem. Phys. 2004;121:4494. doi: 10.1063/1.1778131. [DOI] [PubMed] [Google Scholar]
  80. Söderhjelm P., Krogh J. W., Karlström G., Ryde U., Lindh R. J. Comput. Chem. 2007;28:1083–1090. doi: 10.1002/jcc.20632. [DOI] [PubMed] [Google Scholar]
  81. Huang G., Fernandez-Garcia G., Badiane I., Camarra M., Freslon S., Guillou O., Daiguebonne C., Totti F., Cador O., Guizouarn T., Le Guennic B., Bernot K. Chem.–Eur. J. 2018;24:6983–6991. doi: 10.1002/chem.201800095. [DOI] [PubMed] [Google Scholar]
  82. Zhang K., Montigaud V., Cador O., Li G.-P., Le Guennic B., Tang J.-K., Wang Y.-Y. Inorg. Chem. 2018;57:8550–8557. doi: 10.1021/acs.inorgchem.8b01269. [DOI] [PubMed] [Google Scholar]
  83. Zhang L., Jung J., Zhang P., Guo M., Zhao L., Tang J., Le Guennic B. Chem.–Eur. J. 2016;22:1392–1398. doi: 10.1002/chem.201503422. [DOI] [PubMed] [Google Scholar]
  84. E cross can be estimated using the following relation: Ecross = (E1(α=75°) + E1(α=105°))/2 – (E1(α=129°) + E1(α=150°))/2 – (E1(α=245°) + E1(α=270°))/2 – (E1(α=310°) + E1(α=330°))/2 (see Fig. 5), where the two α values immediately before and after the avoided crossing points (α = 90°, 140°, 260°, and 320°) are considered.
  85. Niu S., Tan M. L., Ichiye T. J. Chem. Phys. 2011;134:134501. doi: 10.1063/1.3569563. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (10.3MB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES