Abstract
Intracortical brain computer interfaces can enable individuals with paralysis to control external devices through voluntarily modulated brain activity. Decoding quality has been previously shown to degrade with signal nonstationarities—specifically, the changes in the statistics of the data between training and testing data sets. This includes changes to the neural tuning profiles and baseline shifts in firing rates of recorded neurons, as well as nonphysiological noise. While progress has been made toward providing long-term user control via decoder recalibration, relatively little work has been dedicated to making the decoding algorithm more resilient to signal nonstationarities. Here, we describe how principled kernel selection with gaussian process regression can be used within a Bayesian filtering framework to mitigate the effects of commonly encountered nonstationarities. Given a supervised training set of (neural features, intention to move in a direction)-pairs, we use gaussian process regression to predict the intention given the neural data. We apply kernel embedding for each neural feature with the standard radial basis function. The multiple kernels are then summed together across each neural dimension, which allows the kernel to effectively ignore large differences that occur only in a single feature. The summed kernel is used for real-time predictions of the posterior mean and variance under a gaussian process framework. The predictions are then filtered using the discriminative Kalman filter to produce an estimate of the neural intention given the history of neural data. We refer to the multiple kernel approach combined with the discriminative Kalman filter as the MK-DKF. We found that the MK-DKF decoder was more resilient to nonstationarities frequently encountered in-real world settings yet provided similar performance to the currently used Kalman decoder. These results demonstrate a method by which neural decoding can be made more resistant to nonstationarities.
1. Introduction
Brain-computer Interfaces (BCIs) use neural information recorded from the brain for the voluntary control of external devices (Wolpaw, Birbaumer, McFarland, Pfurtscheller, & Vaughan, 2002; Hochberg et al., 2006; Schwartz, Cui, Weber, & Moran, 2006; Lebedev & Nicolelis, 2006, 2017; Fetz, 2007; Chestek et al., 2009; Carmena, 2013; Chhatbar & Francis, 2013). At the heart of BCI systems is the decoder: the algorithm that maps neural information to a signal used to control external devices. Modern intracortical BCI decoders used by people with paralysis infer a relationship between neural features (e.g., neuronal firing rates) and the motor intentions from training data. Hence, high-quality control of an external effector, such as a computer cursor, is predicated on appropriate selection of a decoding algorithm.
Decoder selection for intracortical BCI (iBCI) systems traditionally has been based on extensive study of cortical physiology. In what are now classic experiments, nonhuman primates were taught to move a planar manipulandum to one of eight different directions (Georgopoulos, Kalaska, Caminiti, & Massey, 1982). The firing rate as a direction of arm movement was parsimoniously modeled as a sinusoidal curve. For each neuron, the vector corresponding to the maximum firing rate (i.e., the phase offset of a cosine function with a period of 360 degrees) is often referred to as the neuron’s “preferred direction.” The population vector algorithm scales the preferred directions of the recorded neurons by their recorded firing rate; the sum is the decoded vector of the intended direction of neural control (Taylor, Tillery, & Schwartz, 2002; Jarosiewicz et al., 2008; Velliste, Perel, Spalding, Whitford, & Schwartz, 2008). Given sufficient diversity in preferred directions, the problem reduces to linear regression: decoding involves learning the least-squares solution to the surface mapping firing rates to kinematic variables (Kass, Ventura, & Brown, 2005). Alternative decoding approaches include modeling the probability of observing a neural spike as a draw from a time-varying Poisson process (Truccolo, Friehs, Donoghue, & Hochberg, 2008; Brown, Barbieri, Ventura, Kass, & Frank, 2002; Ba, Temereanca, & Brown, 2014; Shanechi et al., 2017), using support-vector regression (Shpigelman, Lalazar, & Vaadia, 2008) or neural networks (Sussillo, Stavisky, Kao, Ryu, & Shenoy, 2016).
An ongoing area of research in iBCI systems is to ensure robust control for the user. Degradation in neural control is often attributed to nonstation-arities in the recorded signals, which are mismatches in the statistics of the neural signals between training and testing models. These include changes to neural tuning profiles, baseline shifts in firing rates, and nonphysiological noise. With linear models, nonstationarities have been shown to degrade decoding performance (Jarosiewicz et al., 2015; Perge et al., 2013). The most common approach to addressing this mismatch is to recalibrate the decoder’s parameters by incorporating more recent neural data. This has been described using batch-based updates with user-defined breaks (Jarosiewicz et al., 2015; Bacher et al., 2015; Gilja et al., 2015), batch-based updates during ongoing use (Orsborn et al., 2014; Shpigelman et al., 2008), and continuous updating during ongoing use (Shanechi, Orsborn, & Carmena, 2016; Dangi, Gowda, Heliot, & Carmena, 2011). Ongoing decoder recalibration traditionally requires information regarding the cursor’s current location and a known target; alternatively, retrospective target inference has been described as a way to label neural data with the BCI user’s intended movement directions based on selections during self-directed onscreen keyboard use (Jarosiewicz et al., 2015).
While attempts to mitigate nonstationarities have largely focused on recalibration, few efforts have aimed to make the decoder inherently more resilient to nonstationarities. To our knowledge, the most extensive study of examining decoder robustness investigated the use of deep neural networks trained from large amounts of offline data (Sussillo et al., 2016). While effective for decoding, this method requires tremendous computational data and resources and required the decoder to be specifically trained to handle nonstationarities using extensive regularization. Other authors have used Bayesian parameter updates for addressing nonstationarities (Li, O’Doherty, Lebedev, & Nicolelis, 2011), or adaptive mean corrections (Homer et al., 2014).
Here, we demonstrate a new decoding algorithm that is more resilient to signal nonstationarities than the currently used linear decoding models. Our approach builds on the previously well-established linear state-space dynamical model for neural decoding. Building on prior work with gaussian process regression (Brandman et al., 2018), the key innovation is making a nonlinear decoder robust to noise through kernel selection and data sparsification. Using both offline simulations and online demonstrations with an iBCI user with paralysis, we demonstrate that our new decoding approach is more resilient to nonstationarities than the standard Kalman filter currently being used in people.
2. Mathematical Methods
We have previously described closed-loop decoding using gaussian process regression in detail (Brandman et al., 2018). Briefly, during calibration, (xi, zi) pairs, representing pairs of neural features and user intention vectors, are collected. We model the neural features as the firing rates and the total power in the bandpass-filtered signal (see section 3.3) and intentions as the unit vector to target (see section 3.4). To perform closed-loop decoding, we compute f (xt), the unfiltered estimate of the user’s intention to control the computer cursor at time t (see section 2.2). We then filter f (xt) using the discriminative Kalman filter (see section 2.1), which provides an estimate of the decoded velocity while incorporating the history of neural features.
Our previous approach to decoding with gaussian process regression used the entire high-dimensional neural data set as the basis for computing the measure of similarity between xt and xi (Brandman et al., 2018). In this letter, we made two important changes to the decoder to increase its robustness to signal nonstationarities. First, we adopted a kernel that calculated the similarity between two neural vectors as the arithmetic average over similarities in each neuron, as opposed to the product that was used by the more standard isotropic gaussian kernel (see section 2.2). This had the effect of limiting the impact any single neuron could have on the calculated similarity between two vectors of neural features. When a nonstationarity occurred in a feature, the decoder “disregarded” this feature without compromising decoding quality. Second, we sparsified the data by averaging (xi, zi) pairs into octants. This dramatically decreased the computational load for real-time decoding. We found that the observed neural features had noise events with surprising frequency (see section 3.1). Averaging across octants had the effect of mitigating the importance of these noisy features for decoding.
2.1. Description of Decoding Method.
In this section, we use the convention that random variables are capital letters and their values are lowercase. For instance, Zt has pdf p(zt). We also emphasize that the i and t subscripts refer to the training and testing data sets, respectively. We model the hidden state-space model with states representing the intended cursor velocity, and the observed states representing the neural features related through the following graphic model:
In typical use, d = 2 (e.g., kinematic computer cursor control), while m = 40 neural features (Jarosiewicz et al., 2013, 2015; Bacher et al., 2015; Brand- man et al., 2018). We are interested in the posterior distribution being the current hidden state given all observations up to the present. Upon specifying the state model that relates how the hidden state changes over time and the measurement model that relates the hidden and observed variables, the posterior can be found recursively using the Chapman-Kolmogorov equation,
| (2.1) |
where α means proportional as a function of zt. The standard Kalman filter is obtained when both the state and measurement models are specified as linear with gaussian noise (Wu et al., 2005; Simeral, Kim, Black, Donoghue, & Hochberg, 2011). Here, we use a stationary linear state model with gaussian noise
| (2.2a) |
| (2.2b) |
where A, S, Γ are d × d, S and Γ are proper covariance matrices, denotes the d-dimensional multivariate normal density with mean μ, and covariance Σ evaluated at a point z. We approximate the measurement model using Bayes’ rule,
| (2.3) |
where is a nonlinear function learned from training data and Q is a d×d covariance matrix. The posterior is then given recursively by
| (2.4) |
| (2.5) |
In this way, we allow the relationship between Xt and Zt to be nonlinear through the function f, while retaining fast, closed-form updates for the posterior. While f can be learned from supervised training data using a number of off-the-shelf discriminative methods (Burkhart, Brandman, Vargas-Irwin, & Harrison, 2016), in this letter, we take f to be the posterior mean from a gaussian process regression and set Q as the covariance of the training data set. We call the resulting filter the discriminative Kalman filter (DKF; Burkhart et al., 2016; Brandman et al., 2018).
2.2. Kernel Selection for Robustness.
As part of decoder calibration, we collect a data set consisting of neural features and intended velocities, which we refer to as These are assumed to be samples from the graphical model and are used to train a gaussian process regression for The gaussian process model takes asymmetric, positive-definite kernel with hyperparameters θ and predicts the mean inferred velocity f(xt) as
| (2.6) |
where Kθ is the n × n matrix given component-wise by is a noise parameter for the training data, In is the n-dimensional identity matrix, vector of the embedding of the training and testing data, and z is an n × 1 vector of the direction vectors of a single dimension. We can reexpress equation 2.6 as a linear combination (see Rasmussen & Williams, 2006 for details):
| (2.7) |
where so that αi is a smoothed version of zi. This demonstrates how the kernel-determined similarity between xi and xt directly determines the impact of the training point (xi, zi) on the prediction f(xt).
In designing a kernel for robust decoding, we select a kernel that ignores large differences between xi and xt that occur along a relatively few number of dimensions. This would potentially make the filter resilient to erratic firing patterns in an arbitrary single neuron.
We use a multiple kernel (MK) approach (Gönen & Alpaydin, 2011) and take
| (2.8) |
where are hyperparameters and xd denotes the dth dimension of x. The similarity between inputs x and y is given as the average over the similarities in each dimension, where all dimensions are equally informative.
To illustrate our choice of kernel, it is helpful to compare it against the more standard isotropic squared exponential kernel, where the sum in equation 2.8 is replaced by a product, as follows:
| (2.9) |
On identical inputs both return their maximum value of indicating that x and y are similar. If, holding all other dimensions equal, the absolute difference grows large (this would occur if readings from a single neuron became very noisy or unreliable), the standard kernel would become arbitrarily small, while the multiple kernel Kθ would never fall below Thus, the multiple kernel continues to identify two neural vectors as close if they differ along only a single arbitrary dimension (see Figure 1 shows a visualization in two dimensions). Note that as m increases beyond two, this difference between the kernels becomes even more pronounced.
Figure 1:
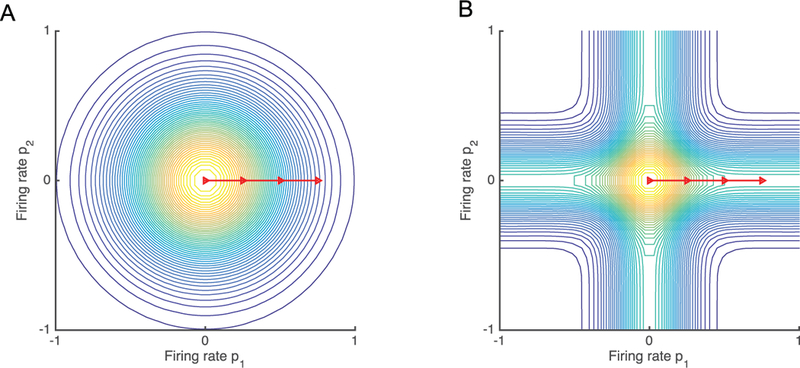
Schematic demonstrating the effect of kernel selection on the measure of similarity for two-dimensional neural features. Since kernel similarity between two points depends on only their coordinate-wise differences, we let p1 = (0, 0) be a point at the origin and consider the kernel-determined similarity between p1 and a second point p2 = (x, y). For each plot, the color at (x, y) represents the measure of similarity according to the selected kernel Traveling along the red line illustrates the effect of increasing the difference in measurements for a single neuron. For the RBF kernel (A), moving along the arrow results in the kernel becoming arbitrarily small. By contrast, the MK kernel (B) never falls below half of the value at the origin as it moves along the arrow. For 40 dimensions, the MK kernel would never fall below 39/40 of its maximal value. Hence, when the RBF kernel is used for closed-loop decoding, nonstationarities from a single neural feature would result in no similarity between the current neural feature and any of the training data. By contrast, the MK kernel will remain relatively unaffected by even a drastic change in a single neuron and continue to effectively use the information from the remaining neurons.
In contrast to data augmentation methods (An, 1996; Sussillo et al., 2016), we do not need to handle dropping neuron i and dropping neuron j separately. Altering our model to accommodate more or different nonstationarities would amount to a simple change in kernel and not result in increased training time.
2.3. Training Set Sparsification for Robustness.
Training data were gathered during a standard radial center-out task during which the user attempted to move the cursor to one of eight equally spaced targets arranged on a circle. We took the (xi, zi) pairs and averaged the neural data over each of the eight targets. The training set used for gaussian process prediction consisted of these eight (xi, zi) pairs. Besides making prediction much faster, we found that using this sparsified training set also increased decoder robustness (see sections 4.1 and 4.2).
3. Experimental Methods
3.1. Permissions.
The Institutional Review Boards of Brown University, Partners Health/Massachusetts General Hospital, and the Providence VA Medical Center, as well as the U.S. Food and Drug Administration, granted permission for this study (Investigational Device Exemption). The participants for this study were enrolled in a pilot clinical trial of the Brain-Gate Neural Interface System.1
3.2. The Participant.
At the time of the study, T10 was a 35-year-old man with a C4 AIS-A spinal cord injury. He underwent surgical placement of two 96-channel intracortical silicon microelectrode arrays (Maynard, Nordhausen, & Normann, 1997) as previously described (Simeral, Kim, Black, Donoghue, & Hochberg, 2011; Kim, Simeral, Hochberg, Donoghue, & Black, 2008). Electrodes were placed into the dominant precentral gyrus and dominant caudal middle frontal gyrus. Closed-loop recording data were used from trial (postimplant) days 259, 265, 272, and 300.
3.3. Signal Acquisition.
Raw neural signals for each electrode were sampled at 30 kHz using the NeuroPort System (Blackrock Microsystems, Salt Lake City, UT) and then processed using the xPC target real-time operating system (Mathworks, Natick, MA). Raw signals were downsampled to 15 kHz for decoding, and then denoised by subtracting an instantaneous common average reference (Jarosiewicz et al., 2015; Gilja et al., 2015) using 40 of the 96 channels on each array with the lowest root-mean-square value. The denoised signals were bandpass-filtered between 250 Hz and 5000 Hz using an eighth-order noncausal Butterworth filter (Masse et al., 2015). Spike events were triggered by crossing a threshold set at 3.5× the root-mean-square amplitude of each channel, as determined by data from a 1-minute reference block at the start of each research session. The following neural features were extracted: the rate of threshold crossings (not spike sorted) on each channel and the total power in the bandpass-filtered signal (Jarosiewicz et al., 2013, 2015; Bacher et al., 2015; Brandman et al., 2018). A total of m = 40 features were selected. Neural features were binned in 20 ms nonoverlapping increments.
3.4. Decoder Calibration.
Task cueing was performed using custom-built software running Matlab (Mathworks, Natick, MA). The participants used standard LCD monitors placed at 55 to 60 cm, at a comfortable angle and orientation. T10 engaged in the radial-8 task as previously described (Jarosiewicz et al., 2013,2015; Bacher et al., 2015; Brandman et al., 2018) (see Figure 2A). Briefly, targets (size = 2.4 cm, visual angle = 2.5°) were presented sequentially in a pseudo-random order, alternating between one of eight radially distributed targets and a center target (radial target distance from center = 12.1 cm, visual angle = 12.6°). Successful target acquisition required the user to place the cursor (size = 1.5 cm, visual angle = 1.6°) within the target’s diameter for 300 ms, before a predetermined time-out (5 seconds). Target time-outs resulted in the cursor moving directly to the intended target, with immediate presentation of the next target.
Figure 2:

(A) Radial-8 task. Eight targets are presented on the screen (blue circle). T10 was instructed to move the cursor (white circle) to the goal (red circle). Targets were acquired when the cursor overlapped the target for 300 ms. (B) Grid task. Square targets were arranged in a grid. T10 was instructed to move the cursor (white circle) to the target (green square). A target was acquired when T10 held the cursor within any square for 1 second. Note that unlike the radial-8 task, incorrect targets were scored.
Each calibration block lasted 3 minutes. During calibration, decoder parameters were updated every 2 to 5 seconds as previously described (Brandman et al., 2018). During the initial stages of calibration, we assisted cursor performance by attenuating the component of the decoded velocity perpendicular to the target (Jarosiewicz et al., 2013; Velliste et al., 2008). This automated assistance was gradually decreased until it was removed 100 to 130 seconds after the start of calibration. The coefficients for the MK-DKF decoder were computed with the calibration block used for the Kalman decoder.
3.5. Noise Injection Experiment.
Once the decoder was calibrated, we sought to investigate the impact of nonstationarities to the MK-DKF and Kalman decoders. Our approach was to have T10 perform the radial-8 task while randomly injecting noise to a single feature and also randomly selecting the decoder currently being used (see Figure 2A).
Each trial ended after either the target was acquired by having the cursor hold within the target for 300 ms or a 5 second time-out. At the start of every noise injection trial, the cursor was recentered over the previously presented target, and the velocity was reset to zero (this ensured that any potential impact of the cursor’s behavior from the previous trial was removed). We performed block randomization of the six experimental conditions: combining one of two decoders (Kalman and MK-DKF) with one of three noise levels (no noise, one z-score, five z-scores). Both the researchers and T10 were blinded to which decoder–noise combination was currently being used. To simulate noise, we provided a z-score offset to the channel with the highest signal-to-noise ratio (Malik et al., 2015), based on the value computed from the calibration block. We standardized the 40 features and the noise-injected feature for both the MK-DKF and Kalman decoders. Experiments were performed in 4 minute blocks.
In order to ensure that T10 was blinded to the decoder and noise combination, we ensured that the kinematic feel of the decoders was similar. That is, we sought to match the mean speed, smoothing, and innovation terms for the two decoders, since these parameters are known to have an impact on decoding quality (Willett et al., 2017). For the radial-8 noise-injection experiment, we matched kinematic parameters in two ways. First, we set the A and Γ of equation 2.5 to match the Kalman values. Second, to ensure that both decoders moved at the same speed, we first computed the mean speed values for Kz in the training block, where K is the Kalman gain matrix. Next, we computed the mean speed value of f (xt) and then linearly scaled f (xt) to match the mean Kz value.
Hence, in performing head-to-head comparisons, we opted to match the kinematics of the MK-DKF decoder to the Kalman. We note that it is very likely that we were having a negative impact on the MK-DKF decoder performance by doing so, since the parameters used were likely suboptimal compared to those that would have been computed.
3.6. Performance Measurement.
We quantified performance using a grid task after locking decoder parameters (Brandman et al., 2018; Pandarinath et al., 2017; Nuyujukian, Fan, Kao, Ryu, & Shenoy, 2015) (see Figure 2B). This task consisted of a grid of 36 square targets arranged in a square grid, where the length of one side of the square grid was 24.2 cm (visual angle = 24.8°). One of targets was presented at a time in a pseudorandom order. Targets were acquired when the cursor was within the area of the square for 1 second. Incorrect selections occurred if the cursor dwelled on a nontarget square for an entire hold period. Each comparison block was 3 minutes in length.
We measured the achieved bit rate (BR), which measures the effective throughput of the system (Nuyujukian et al., 2015),
where N is the number of possible selections; Sc and Si are the number of correctly and incorrectly selected targets, respectively; and t is the elapsed time within the block.
3.7. Offline Analysis.
We retrospectively analyzed data collected from previous research sessions. We restricted our analysis to sessions where T10 moved a computer cursor using motor imagery. He acquired targets using the radial-8 task, the grid task, or free typing tasks (Jarosiewicz et al., 2015).
3.7.1. Injecting Noise for the MK-DKF and Kalman Decoders.
To investigate the impact of noise on decoder performance, we performed offline simulations of both the Kalman and MK-DKF decoders. We computed the angular error between the predicted decoder value without filtering (i.e., the Kz term and the f(xt) terms of the Kalman and MK-DKF decoders, respectively) and the label modeled as the vector from cursor to target (Simeral et al., 2011; Brandman et al., 2018). Data from a single research session were concatenated together. A decoder was trained using half of the data available for a session without replacement and then used to predict the mean angular error for the other half of the data set. Decoder predictions were bootstrapped 100 times.
3.7.2. Offline Assessment of Noise.
Our standard practice is to normalize real-time neural features using the mean and the standard deviation of the previous block’s worth of data; this is done to mitigate the effect of signal nonstationarities (Jarosiewicz et al., 2015). We also use m = 40 features, selected according to a signal-to-noise ratio (Malik et al., 2015).
As part of the offline analysis, for each session, we incrementally calibrated Kalman decoders in chronological order of recorded blocks. We then computed the number of times a feature exceeded a z-score offset in the next block. For instance, to compute the number of noise events at two z-scores for trial day 295, block 5, we computed the z-score mean and standard deviations based on data for blocks 1 to 4 and then counted the number of 20 ms blocks with deviations more than two z-scores away from the mean for each feature.
4. Results
4.1. Offline Analysis: Quantifying the Effect of Noise on Closed-Loop Neural Decoding.
We investigated the impact of noise injection for both the Kalman and MK-DKF decoders by performing offline simulations of previously collected data. There were 124 research sessions recorded from participant T10. We identified 96 sessions and a total of 48.2 hours of closed-loop neural control of a computer cursor, during which many variations of strapped the data 100 times into nonoverlapping training and testing sets (50–50 splits), and then used the training data set to compute the coefficients for both the Kalman and MK-DKF decoders. We measured decoder performance using the predicted angular error between the simulated decoded direction and the known vector from cursor to target (see section 3.7.1).
Our implementation of the Kalman decoder for closed-loop neural control (Jarosiewicz et al., 2015; Bacher et al., 2015; Brandman et al., 2018) uses a measure of signal-to-noise to subselect 40 of the 384 features to be used in closed-loop decoding (Malik et al., 2015). We added noise to the single feature with the highest signal-to-noise ratio in the testing data set (see Figure 3A). With the Kalman decoder, we found a nearly linear relationship between the amount of injected noise and the percent change in angular error (R2 = 0.994, p < 10–24). We then repeated this experiment using the same features for both calibration and noise injection with the MK-DKF decoder. We found that noise injection had only minimal changes to the MK-DKF performance despite large noise injection values.
Figure 3:
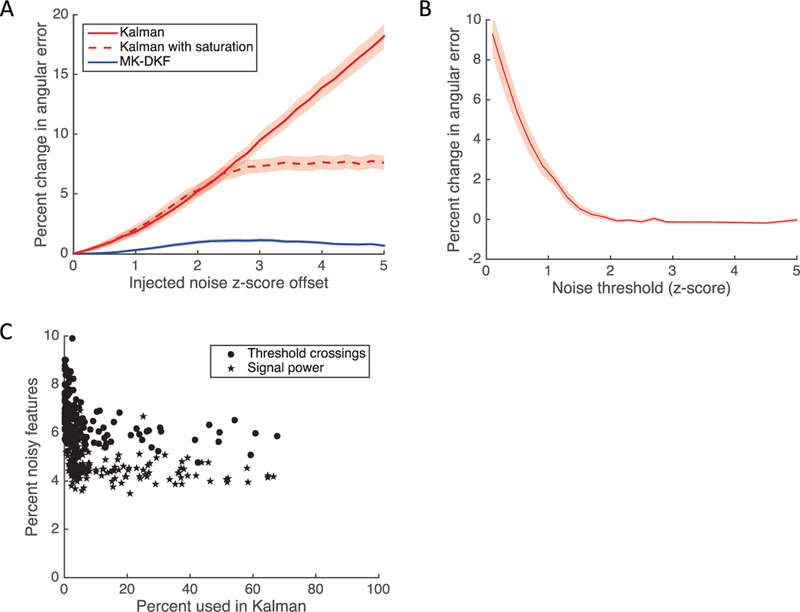
(A) Change in angular error as a function of z-score offset for the Kalman filter, the Kalman filter with feature saturation, and MK-DKF decoders. We identified 96 research sessions where T10 performed closed-loop neural control. For each session, we performed a 50–50 split of the data and used the training data to compute the coefficients for the decoders; then we predicted the angular error on the testing data. Next, we added a z-score offset to a single channel (standardized for each decoder). The shaded areas represent the standard error of measurement for each decoder. (B) Change in angular error as a function of feature thresholding. During the bootstrapping procedure, we saturated features for both the training and testing data sets and computed the change in angular error compared to no saturation. The shaded area represents the standard error of measurement. (C) Examining the frequency of noise events. For each of the bootstrapped simulations, we counted the frequency at which each feature was incorporated into the decoder (m = 40), as well as the frequency at which the feature was observed to deviate by more than two z-scores.
Given the detrimental effect of z-score offsets on decoding performance, a straightforward solution would be to simply saturate the features used for decoding. That is, all values greater than a saturation value (e.g., two z-scores) would be set to the saturation value. We computed the change in angular error as a function of feature saturation threshold (see Figure 3B). We found that the angular error decreased as saturation levels increased, reaching the base performance at two z-scores. These results suggested that features could be saturated at two z-scores without a negative impact on decoding performance.
Next, we quantified the frequency at which two z-score noise events occurred. Across all features, the two z-score deviations occurred 5.6% ±1.2 (SD) of observed 20 ms bins (see Figure 3C). Importantly, the same features that had large noise events were those that were highly informative and incorporated into the Kalman filter according to the feature’s SNR (Malik et al., 2015). Since real-time neural decoding is commonly performed in 20 ms bins, these results suggest that apparent noise events are observed roughly three times per second with our current clinical research-grade neural recording setup.
Intuitively, the data sparsification used with the MK-DKF decoder should result in lower performance with the Kalman filter. Sparsification of the linear data set would result in the regression variance being greatly underestimated, and hence result in lower offline decoding performance. To quantify the effect of sparsification with the Kalman, we averaged the training data into octants and computed performance using mean angular error. For 95 of the 96 experimental sessions, sparsifying the data resulted in a statistically significant increase in mean angular error (paired t-test with Bonferonni correction, p < 0.05), with an overall mean increase of 16% ± 2 (SD).
Taken together, these results suggest that (1) the Kalman decoder is highly sensitive to z-score offsets, even arising from a single feature; (2) z-score offsets that degrade decoding performance for the Kalman occur approximately three times per second; and (3) principled thresholding of features will alleviate some of the effects of z-score offsets. These results also suggest that the MK-DKF is relatively insensitive to z-score offsets for single features.
4.2. Online Analysis: Closed-Loop Assessment of Both the Kalman and MK-DKF Decoders.
We characterized the effect that noise events had on closed-loop neural decoding with T10 (see Figure 4A, supplementary movie 1 online). At the start of the research session, we first calibrated both the Kalman and MK-DKF decoders and then matched their kinematic coefficients and the subset of features used for decoding (see section 3.5). Next, we performed a double-blinded randomization procedure where both the decoder and the amount of noise injected were randomly selected every two targets. Neither T10 nor the researchers were aware of the current decoder/noise combination. Noise was injected by offsetting the z-score of a single feature, standardized for both decoders (see section 3.5).
Figure 4:
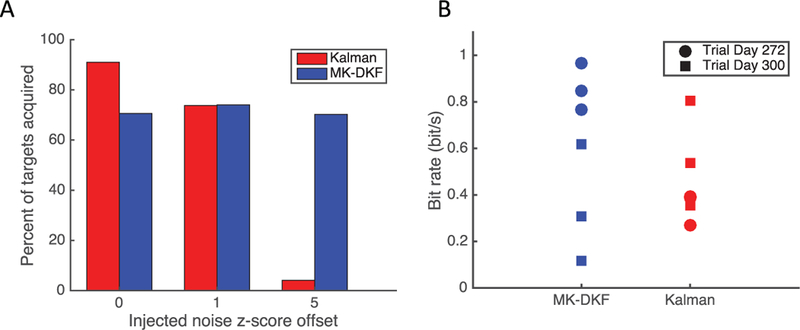
(A) Percentage of targets acquired during closed-loop cursor control by T10 in the radial-8 task. On research days 259, 265, 272, and 300, T10 acquired targets wherein the decoder (Kalman and MK-DKF) and the amount of noise (no noise, one z-score, five z-scores) were randomly selected. There was no statistically significant difference in performance across the noise injection trials for the MK-DKF decoder (χ2, p = 0.81) There was a statistically significant difference across conditions for the Kalman decoder (χ 2, p < 10–37). To ensure that T10 could not distinguish between which decoder was being used, the kinematic parameters of the MK-DKF matched to the Kalman decoder. (B) Performance of both the MK-DKF and Kalman decoders with optimal kinematic parameters. There was no statistically significant difference in bit rate between the two decoders (trial days 272 and 300, Wilcoxon rank-sum test p = 0.48).
T10 was presented with 596 targets in a center-out task over three research sessions (trial days 259, 265, and 272). For the Kalman decoder, there was a statistically significant dose-dependent response between the amount of injected noise (no noise, one z-score offset, and five z-score offsets) and the percentage of targets acquired within a 5 second time-out (χ2, p < 10–37). By contrast, there was no statistically significant difference between the three noise conditions with the MK-DKF decoder (χ2, p = 0.81).
We note that in this comparison, the percentage of targets acquired by the MK-DKF decoder was inferior to that of the Kalman decoder without injected noise (see Figure 4A). In order to have performed this comparison, we matched the kinematic coefficients of the MK-DKF to the Kalman decoder (see section 3.5). This ensured that the “feel” of the decoders was indistinguishable, allowing us to perform the randomized experiment. However, in so doing, we were likely selecting suboptimal kinematic coefficients for the decoder.
To quantify the performance of both decoders without injected noise and with optimal kinematic parameters, we calibrated the Kalman and MK-DKF decoders using their respective optimal kinematic coefficients. After decoder calibration, T10 acquired targets in the grid task, and the decoder being used was alternated every block (see Figure 4B). There was no statistically significant difference in bit rate between the two decoders (trial days 272 and 300, N = 12 blocks, Wilcoxon rank-sum test p = 0.48).
5. Discussion
A new neural decoder based on gaussian process regression (MK-DKF) was more resilient to noise than the traditionally used linear decoding strategy used for closed-loop neural control. When z-score offsets were added to single channels in the Kalman filter, the decoding performance degraded; this was not seen with the MK-DKF decoding approach. After optimizing the parameterizations of both decoders, the communication bit rate was not statistically different.
5.1. Addressing Nonstationarities in Neural Data.
Robust and reliable control with an intracortical brain-computer interface is predicated on the properties of the decoding algorithm selected to map high-dimensional neural features to low-dimensional commands used to control external effectors. End-effector control degrades without recalibration of decoder parameters (Jarosiewicz et al., 2015; Perge et al., 2013). To this end, multiple solutions have been proposed to recalibrate decoders based on closed-loop neural data during use, either when targets are known (Hochberg et al., 2006, 2012; Kim et al., 2008; Jarosiewicz et al., 2013; Collinger et al., 2013; Wodlinger et al., 2015; Gilja et al., 2015; Orsborn et al., 2014; Shanechi et al., 2017; Dangi et al., 2011; Carmena, 2013) or retrospectively inferred (Jarosiewicz et al., 2015). Other approaches have investigated BCI decoder robustness using a wide variety of specific methods, including adapting a discriminative Bayesian filter (Brandman et al., 2018), refitting a Kalman filter (Gilja et al., 2012; Dangi, Orsborn, Moorman, & Carmena, 2013), Bayesian updating for an unscented Kalman filter (Li et al., 2011), reweighting a naive Bayes classifier (Bishop et al., 2014), retraining a kernelized ARMA model (Shpigelman et al., 2008), and reinforcement learning (Mahmoudi, Pohlmeyer, Prins, Geng, & Sanchez, 2013; Pohlmeyer, Mahmoudi, Geng, Prins, & Sanchez, 2014), among others.
Rather than adapting the coefficients of the decoder given new closed- loop data, the goal of robust model selection is to design the decoder to be more resilient to nonstationarities. One previously described decoder achieved robustness with a multiplicative recursive neural network and augmenting the training data with perturbations that mimicked the desired nonstationities against which they wished to train (Sussillo et al., 2016). For example, in order to train against dropping the ith neuron, exemplars were added to the training data set where the ith neuron had been zeroed out. This technique of augmenting a training set with noisy data is well established for increasing generalization performance in neural networks and is commonly referred to as data augmentation (An, 1996). It requires generating and training over new artificial data for each individual targeted nonstationarity for each feature. Hence, exemplars generated to protect the decoder against dropping the ith feature do not protect against dropping the jth feature.
While effective, there are limitations in applying data augmentation for closed-loop BCI systems for human users. First, one of the goals of pursuing iBCI research for people is to develop devices that are intuitive and easy to use, with minimal technician oversight, and require minimal calibration time. It would not be possible to apply a deep neural network with a bagging technique in the case where the user is using the system with limited available data, such as using the system for the first time (Brandman et al., 2018). Second, the system requires significant computational resources. Bagging enlarges an already massive data set by orders of magnitude, entailing a commensurate increase in training burden for the neural network. At least with today’s available hardware and the requirement for local computation, the increase in computational resources would not be possible for portable iBCI systems to be used inside homes. By contrast, the MK-DKF decoder did not require explicit training to acquire robustness. The robust kernel design was able to distinguish between signal and noise within 3 minutes of calibration.
We note that one straightforward approach to decoder robustness with a linear decoding strategy such as the Kalman filter would be to saturate features. We found that saturating the neural features beyond two z-scores did not have a negative impact on offline decoder performance (see Figure 3B), making the decoder resistant to large feature deviations (see Figure 3A). The MK-DKF decoder did not require explicit training or setting a signal saturation threshold to acquire robustness. The robust kernel design was able to distinguish between signal and noise within 3 minutes of calibration.
While a z-score offset to the Kalman would be predicted to result in a degradation in performance, it was not known a priori the extent to which a user would be able to compensate for the bias that would develop during closed-loop performance. We have previously described how closed-loop cursor control degrades with a baseline shift in firing rate of a neuron, resulting in a cursor bias (Perge et al., 2013), and described strategies that may be used to enhance control for the user (Jarosiewicz et al., 2015). Our results quantified the effect of signal degradation as a function of z-score offset. We did not observe a noise-dependent degradation of the MK-DKF decoder and demonstrated its resistance compared to the Kalman filter.
5.2. Experimental Design.
To our knowledge, our methodological approach to comparing decoders by randomly interleaving decoders in real time has not been described in the human iBCI literature. There are two alternative research designs that we could have taken. First, we could have tested the Kalman on one day and the MK-DKF on the next. However, the experience of multiple iBCI groups (Jarosiewicz et al., 2015; Collinger et al., 2013; Bouton et al., 2016) suggests that decoder performance may change dramatically from day to day. Hence, this approach would need a large number of research sessions to demonstrate changes in decoder performance that could not be better explained by signal interday nonstationarities. We opted not to take this approach in the interest of decreasing the amount of session time where the user was deliberately presented with a decoder that would “break” periodically from noise injection.
Second, we could have calibrated a decoder and then immediately tested it (Kalman), and then switched decoders and repeated the procedure (MK-DKF). Indeed, this block-by-block approach has already been described in examining the neural decoding using gaussian process regression (Brandman et al., 2018). However, T10 had previously told us that trying to use a decoder when it “wasn’t working properly” was “hard work.” In fact, he would stop trying to control the cursor when he thought it was not working well as he was already aware that “we could do better.” Given that we were deliberately causing the decoder not to work properly by noise injection, it was important for us not to design an experiment where T10 would simply give up if he knew which decoder was currently being used. Hence, blinding T10 to the decoder became critical.
We note that the goal of this experiment was to compare two different decoding algorithms with a similar linear state-space decoding setup. However, the kinematic parameters used in linear state-space-models have a substantial effect on decoding performance (Willett et al., 2017). Hence, in order to isolate exactly the effect of the decoder, we needed to ensure that all of the relevant variables of kinematic parameters were controlled. We designed an experiment where T10, as well as the researchers in the room, would be blinded to the decoder and the amount of injected noise.
5.3. Growth Directions for MK-DKF.
Our implementation of the MK-DKF decoder provides an exciting foundation from which to explore decoder robustness. For instance, our approach naively provided a uniformly weighted linear addition of multiple kernels, thereby making the explicit assumption that each feature is equally important for decoding. One approach would be to incorporate techniques in kernel learning (Gonen & Alpaydin, 2011). For instance, one could learn a convex sum of weights for the linear combination of kernels that “align:” to a training kernel (Cortes, Mohri, & Rostamizadeh, 2012). Alternatively, one could be explore alternative distance metrics. For instance, rather than using Euclidean distances between features, one could apply a spike train distance metric (Victor & Purpura, 1997). This metric can be adapted as a valid kernel embedding function and used for decoding neural data (Park, Seth, Paiva, Li, & Principe, 2013; Brockmeier et al., 2014; Li, Brockmeier, Choi, Francis, Sanchez, & Principe, 2014). It has also been shown to perform better than Euclidean distances when visualizing complex neuronal data sets (VargasIrwin, Brandman, Zimmermann, Donoghue, & Black, 2015).
6. Conclusion
BCIs have the potential improve the quality of life for people with paralysis. Here we present experimental evidence that a decoder using gaussian process regression is robust to nonstationarities in neural signals compared to the previously used Kalman filter.
Supplementary Material
Acknowledgments
We thank participant T10 and his family; B. Travers and D. Rosler for administrative support; C. Grant for clinical assistance; and Arthur Gretton for discussions on kernel selection. This work was supported by the National Institutes of Health: National Institute on Deafness and Other Communication Disorders (NIDCD R01DC009899), Rehabilitation Research and Development Service, Department of Veterans Affairs (B6453R and N9228C); National Science Foundation (DMS1309004); National Institutes of Health (IDeA P20GM103645, R01MH102840); Massachusetts General Hospital (MGH)—Deane Institute for Integrated Research on Atrial Fibrillation and Stroke; Joseph Martin Prize for Basic Research; the MGH Executive Committee on Research (ECOR) of Massachusetts General Hospital; Canadian Institute of Health Research (336092); Killam Trust Award Foundation; and Brown Institute of Brain Science. The content of this letter is solely our responsibility and does not necessarily represent the official views of the National Institutes of Health, the Department of Veterans Affairs, or the U. S. government.
Footnotes
ClinicalTrials.gov Identifier: NCT00912041. Caution: Investigational device. Limited by federal law to investigational use.
Contributor Information
David M. Brandman, Neuroscience Graduate Program, Department of Neuroscience, Carney Institute for Brain Science, and School of Engineering, Brown University, Providence, RI02912, U.S.A.; and Department of Surgery (Neurosurgery), Dalhousie University, Halifax, NS B3H 347 Canada
Michael C. Burkhart, Division of Applied Mathematics, Brown University, Providence, RI 02912, U.S.A.
Jessica Kelemen, Center for Neurotechnology and Neurorecovery, Neurology, Massachusetts General Hospital, Boston, MA 02114, U.S.A..
Brian Franco, Center for Neurotechnology and Neurorecovery, Neurology, Massachusetts General Hospital, Boston, MA 02114, U.S.A..
Matthew T. Harrison, Division of Applied Mathematics, Brown University, Providence, RI 02912, U.S.A.
Leigh R. Hochberg, Center for Neurorestoration and Neurotechnology, Rehabilitation R&D Service, Department of Veterans Affairs Medical Center, Providence, RI 02908; Carney Institute for Brain Science and School of Engineering, Brown University, Providence, RI 02912; Center for Neurotechnology and Neurorecovery, Neurology, Massachusetts General Hospital, Boston, MA 02114; and Neurology, Harvard Medical School, Boston, MA 02115, U.S.A.
References
- An G (1996). The effects of adding noise during backpropagation training on a generalization performance. Neural Comput, 8(3), 643–674. [Google Scholar]
- Ba D, Temereanca S, & Brown EN (2014). Algorithms for the analysis of ensemble neural spiking activity using simultaneous-event multivariate point-process models. Frontiers in Computational Neuroscience, 8, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacher D, Jarosiewicz B, Masse NY, Stavisky SD, Simeral JD, Newell K, … Hochberg LR (2015). Neural point-and-click communication by a person with incomplete locked-in syndrome. Neurorehabilitation and Neural Repair, 29(5), 462–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop W, Chestek CC, Gilja V, Nuyujukian P, Foster JD, Ryu SI,… Yu BM (2014). Self-recalibrating classifiers for intracortical brain-computer interfaces. J. Neural Eng, 11(2), 026001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouton CE, Shaikhouni A, Annetta NV, Bockbrader MA, Friedenberg DA, Nielson DM, … Rezai AR (2016). Restoring cortical control of functional movement in a human with quadriplegia. Nature, 533, 247–250. [DOI] [PubMed] [Google Scholar]
- Brandman DM, Hosman T, Saab J, Burkhart MC, Shanahan BE, Ciancibello JG, … Hochberg LR (2018). Rapid calibration of an intracortical brain-computer interface for people with tetraplegia. Journal of Neural Engineering, 15(2), 026007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockmeier AJ, Choi JS, Kriminger EG, Francis JT, & Principe JC (2014). Neural decoding with kernel-based metric learning. Neural Computation, 26(6), 1080–1107. [DOI] [PubMed] [Google Scholar]
- Brown E, Barbieri R, Ventura V, Kass R, & Frank L (2002). The time-rescaling theorem and its application to neural spike train data analysis. Neural Computation, 14(2), 325–346. [DOI] [PubMed] [Google Scholar]
- Burkhart MC, Brandman DM, Vargas-Irwin CE, & Harrison MT (2016). The discriminative Kalman filter for nonlinear and non-gaussian sequential Bayesian filtering. arXiv:1608/06622 [stat ML]. [Google Scholar]
- Carmena JM (2013). Advances in neuroprosthetic learning and control. PLoS Biology, 11(5), 1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chestek CA, Cunningham JP, Gilja V, Nuyujukian P, Ryu SI, & Shenoy KV (2009). Neural prosthetic systems: Current problems and future directions. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (pp. 3369–3375). Piscataway, NJ: IEEE. [DOI] [PubMed] [Google Scholar]
- Chhatbar PY, & Francis JT (2013). Towards a naturalistic brain-machine interface: Hybrid torque and position control allows generalization to novel dynamics. PLoS One, 8(1), e52286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collinger JL, Wodlinger B, Downey JE, Wang W, Tyler-Kabara EC, Weber DJ,… Schwartz AB (2013). High-performance neuroprosthetic control by an individual with tetraplegia. Lancet, 381(9866), 557–564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes C, Mohri M, & Rostamizadeh A (2012). Algorithms for learning kernels based on centered alignment. Journal of Machine Learning, 13, 795–828. [Google Scholar]
- Dangi S, Gowda S, Heliot R, & Carmena JM (2011). Adaptive Kalman filtering for closed-loop brain-machine interface systems. In Proceedings of the 2011 5th International IEEE/EMBS Conference on Neural Engineering (pp. 609–612). Piscataway, NJ: IEEE. [Google Scholar]
- Dangi S, Orsborn AL, Moorman HG, & Carmena JM (2013). Design and analysis of closed-loop decoder adaptation algorithms for brain-machine interfaces. Neural Comput, 25(7), 1693–1731. [DOI] [PubMed] [Google Scholar]
- Fetz EE (2007). Volitional control of neural activity: Implications for brain-computer interfaces. Journal of Physiology, 579(Pt. 3), 571–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos A, Kalaska J, Caminiti R, & Massey J (1982). On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. Journal of Neuroscience, 2(11), 1527–1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilja V, Nuyujukian P, Chestek CA, Cunningham JP, Yu BM, Fan JM, … Shenoy KV (2012). A high-performance neural prosthesis enabled by control algorithm design. Nat. Neurosci, 15(12), 1752–1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilja V, Pandarinath C, Blabe CH, Nuyujukian P, Simeral JD, Sarma AA, … Henderson JM (2015). Clinical translation of a high-performance neural prosthesis. Nature Medicine, 21(10), 1142–1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gönen M, & Alpaydin E (2011). Multiple kernel learning algorithms. Journal of Machine Learning Research, 12,2211–2268. [Google Scholar]
- Hochberg LR, Bacher D, Jarosiewicz B, Masse NY, Simeral JD, Vogel J, … Donoghue JP (2012). Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature, 485(7398), 372–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, … Donoghue JP (2006). Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature, 442(7099), 164–171. [DOI] [PubMed] [Google Scholar]
- Homer ML, Perge JA, Black MJ, Harrison MT, Cash SS, & Hochberg LR (2014). Adaptive offset correction for intracortical brain-computer interfaces. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 22(2), 239–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosiewicz B, Chase SM, Fraser GW, Velliste M, Kass RE, & Schwartz AB (2008). Functional network reorganization during learning in a brain-computer interface paradigm. Proceedings of the National Academy of Sciences of the United States of America, 105(49), 19486–19491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosiewicz B, Masse NY, Bacher D, Cash SS, Eskandar E, Friehs G, .. . Hochberg LR (2013). Advantages of closed-loop calibration in intracortical brain-computer interfaces for people with tetraplegia. Journal of Neural Engineering, 10(4), 046012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosiewicz B, Sarma AA, Bacher D, Masse NY, Simeral JD, Sorice B, … Hochberg LR (2015). Virtual typing by people with tetraplegia using a self-calibrating intracortical brain-computer interface. Science Translational Medicine, 7(313), 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kass RE, Ventura V, & Brown EN (2005). Statistical issues in the analysis of neuronal data. J. Neurophysiol, 94, 8–25. [DOI] [PubMed] [Google Scholar]
- Kim S-P, Simeral JD, Hochberg LR, Donoghue JP, & Black MJ (2008). Neural control of computer cursor velocity by decoding motor cortical spiking activity in humans with tetraplegia. Journal of Neural Engineering, 5(4), 455–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebedev MA, & Nicolelis MAL (2006). Brain-machine interfaces: Past, present and future. Trends in Neurosciences, 29(9), 536–546. [DOI] [PubMed] [Google Scholar]
- Lebedev MA, & Nicolelis MA (2017). Brain-machine interfaces: From basic science to neuroprostheses and neurorehabilitation. Physiol. Rev, 97(2), 767–837. [DOI] [PubMed] [Google Scholar]
- Li L, Brockmeier AJ,Choi JS, Francis JT, Sanchez JC, & Principe JC (2014). A tensor-product-kernel framework for multiscale neural activity decoding and control. Computational Intelligence and Neuroscience, 2014, art. 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, O’Doherty JE, Lebedev MA, & Nicolelis MA (2011). Adaptive decoding for brain-machine interfaces through Bayesian parameter updates. Neural Comput, 23(12), 3162–3204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmoudi B, Pohlmeyer EA, Prins NW, Geng S, & Sanchez JC (2013). Towards autonomous neuroprosthetic control using Hebbian reinforcement learning. J. Neural Eng, 10(6), 066005. [DOI] [PubMed] [Google Scholar]
- Malik WQ, Hochberg LR, Donoghue JP, Brown EN, Member S, Hochberg LR,… Brown EN (2015). Modulation depth estimation and variable selection in state-space models for neural interfaces. IEEE Trans. Biomed. Eng, 62(2), 570–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masse NY, Jarosiewicz B, Simeral JD, Bacher D, Stavisky SD, Cash SS, … Donoghue JP (2015). Non-causal spike filtering improves decoding of movement intention for intracortical BCIs. Journal of Neuroscience Methods, 244,94–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard EM, Nordhausen CT, & Normann RA (1997). The Utah intracortical electrode array: A recording structure for potential brain-computer interfaces. Electroencephalography and Clinical Neurophysiology, 102(3), 228–239. [DOI] [PubMed] [Google Scholar]
- Nuyujukian P, Fan JM, Kao JC, Ryu SI, & Shenoy KV (2015). A highperformance keyboard neural prosthesis enabled by task optimization. IEEE Transactions on Biomedical Engineering, 62(1), 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orsborn AL, Moorman HG, Overduin SA, Shanechi MM, Dimitrov DF, & Carmena JM (2014). Closed-loop decoder adaptation shapes neural plasticity for skillful neuroprosthetic control. Neuron, 82(6), 1380–1393. [DOI] [PubMed] [Google Scholar]
- Pandarinath C, Nuyujukian P, Blabe CH, Sorice BL, Saab J, Willett F,… Henderson JM (2017). High performance communication by people with paralysis using an intracortical brain-computer interface. eLife, 1–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park IM, Seth S, Paiva ARC, Li L, & Principe JC (2013). Kernel methods on spike train space for neuroscience: A tutorial. IEEE Signal Processing Magazine, 30(4), 149–160. [Google Scholar]
- Perge JA, Homer ML, Malik WQ, Cash S, Eskandar E, Friehs G, … Hochberg LR (2013). Intra-day signal instabilities affect decoding performance in an intracortical neural interface system. Journal of Neural Engineering, 10(3), 036004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohlmeyer EA, Mahmoudi B, Geng S, Prins NW, & Sanchez JC (2014). Using reinforcement learning to provide stable brain-machine interface control despite neural input reorganization. PLoS One, 9(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen CE, & Williams CKI (2006). Gaussian processes for machine learning. Cambridge, MA: MIT Press. [Google Scholar]
- Schwartz AB, Cui XT, Weber DJ, & Moran DW (2006). Brain-controlled interfaces: Movement restoration with neural prosthetics. Neuron, 52(1), 205–220. [DOI] [PubMed] [Google Scholar]
- Shanechi MM, Orsborn AL, & Carmena JM (2016). Robust brain-machine interface design using optimal feedback control modeling and adaptive point process filtering. PLoS Computational Biology, 12(4), 1–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanechi MM, Orsborn AL, Moorman HG, Gowda S, Dangi S, & Carmena JM (2017). Rapid control and feedback rates enhance neuroprosthetic control. Nature Communications, 8, 13825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shpigelman L, Lalazar H, & Vaadia E (2008). Kernel-ARMA for hand tracking and brain-machine interfacing during 3D motor control In Koller D, Schuurmans D, Bengio Y, & Bottou L (Eds.), Neural information processing systems, 21 (pp. 1489–1496). Red Hook, NY: Curran. [Google Scholar]
- Simeral JD, Kim S-P, Black MJ, Donoghue JP, & Hochberg LR (2011). Neural control of cursor trajectory and click by a human with tetraplegia 1000 days after implant of an intracortical microelectrode array. Journal of Neural Engineering, 8(2), 025027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sussillo D, Stavisky SD, Kao JC, Ryu SI, & Shenoy KV (2016). Making brain-machine interfaces robust to future neural variability. Nature Communications, 7, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor DM, Tillery SIH, & Schwartz AB (2002). Direct cortical control of 3D neuroprosthetic devices. Science, 296(5574), 1829–1832. [DOI] [PubMed] [Google Scholar]
- Truccolo W, Friehs GM, Donoghue JP, & Hochberg LR (2008). Primary motor cortex tuning to intended movement kinematics in humans with tetraplegia. Journal of Neuroscience, 28(5), 1163–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vargas-Irwin CE, Brandman DM, Zimmermann JB, Donoghue JP, & Black MJ (2015). Spike train SIMilarity Space (SSIMS): A framework for single neuron and ensemble data analysis. Neural Computation, 27(1), 1–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velliste M, Perel S, Spalding MC, Whitford AS, & Schwartz AB (2008). Cortical control of a prosthetic arm for self-feeding. Nature, 453(7198), 1098–1101. [DOI] [PubMed] [Google Scholar]
- Victor J, & Purpura K (1997). Metric-space analysis of spike trains: Theory, algorithms and application. Network: Computation in Neural Systems, 8(2), 127–164. [Google Scholar]
- Willett FR, Pandarinath C, Jarosiewicz B, Murphy BA, Memberg WD, Blabe CH, … Ajiboye AB (2017). Feedback control policies employed by people using intracortical brain-computer interfaces. Journal of Neural Engineering, 14(1), 16001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wodlinger B, Downey JE, Tyler-Kabara EC, Schwartz AB, Boninger ML, & Collinger JL (2015). Ten-dimensional anthropomorphic arm control in a human brain machine interface: Difficulties, solutions, and limitations. Journal of Neural Engineering, 12(1), 016011. [DOI] [PubMed] [Google Scholar]
- Wolpaw JR, Birbaumer N, McFarland DJ, Pfurtscheller G, & Vaughan TM (2002). Brain-computer interfaces for communication and control. Clinical Neurophysiology, 113(6), 767–791. [DOI] [PubMed] [Google Scholar]
- Wu W, Gao Y, Bienenstock E, Donoghue JP, Black MJ, Biemenstock E,… Black MJ (2005). Bayesian population decoding of motor cortical activity using a Kalman filter. Neural Computation, 18(1), 80–118. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


