Trial-by-trial source-resolved EEG responses to gait task challenges predict subsequent step adaptation

Abstract

A growing body of evidence indicates a pivotal role of cognition and in particular executive function in gait control and fall prevention. In a recent gait study using electroencephalographic (EEG) imaging, we provided direct proof for cortical top-down inhibitory control in step adaptation. A crucial part of motor inhibition is recognizing stimuli that signal the need to inhibit or adjust motor actions such as steps during walking. One of the EEG signatures of performance monitoring in response to events signaling the need to adjust motor responses, are error-related potential (error-ERP) features. To examine whether error-ERP features may index executive control during gait adaptation, we analyzed high-density (108-channel) EEG data from an auditory gait pacing study. Participants (N = 18) walking on a steadily moving treadmill were asked to step in time to an auditory cue tone sequence, and then to quickly adapt their step length and rate, to regain step-cue synchrony following occasional unexpected shifts in the pacing cue train to a faster or slower cue tempo. Decomposition of the continuous EEG data by independent component analysis revealed a negative deflection in the source-resolved event-related potential (ERP) time locked to ‘late’ cue tones marking a shift to a slower cue tempo. This vertex-negative ERP feature, localized primarily to posterior medial frontal cortex (pMFC) and peaking 250 ms after the onset of the tempo-shift cue, we here refer to as the step-cue delay negativity (SDN). SDN source, timing, and polarity resemble other error-related ERP features, e.g., the Error-Related Negativity (ERN) and Feedback-Related Negativity (FRN) in (seated) button press response tasks. In single trials, SDN amplitude varied with the magnitude of the cue latency deviation (the time interval between the expected and actual cue onsets). Regression analysis also identified linear coupling between SDN amplitude and the subsequent speed of gait tempo adaptation (as measured by the increase in length of the ensuing adaptation step). The SDN in this paradigm thus seems both to index the perceived need for and the subsequent magnitude of the immediate gait adjustment, consistent with performance-monitoring models. Future research might investigate relationships of these control processes to the impairment of gait adjustment in motor disorders and cognitive decline, for example to develop a biomarker for fall risk prediction in early-stage Parkinson’s.

1. Introduction

The relationship between age- and/or disease-associated decline in cognitive function and reduced mobility is an increasingly important topic for investigation. A growing body of evidence indicates a pivotal role of cognition and in particular executive function (EF) in gait control and fall prevention (Mirelman et al., 2012, Lamb et al., 2005). Elderly persons prone to falls perform more poorly than healthy controls on attention and EF tests (Hausdorff et al., 2006), and higher risk of falls in elderly is predicted by poorer performance on EF and attention tests five years earlier (Mirelman et al., 2012). It is under debate, however, whether EF only helps mitigating the risk of falls by compensating for age-related motor impairment, or whether EF is needed to master normal and challenging gait tasks including step planning and response to physical and environmental gait challenges.

Recent studies of brain support for gait in unimpaired subjects provide evidence that EF is directly involved in normal and challenging gait tasks suggesting that a decline in EF may directly affect the ability for flexible gait (De Sanctis et al., 2014, Wagner et al, 2016). These studies have been abetted by advances in signal processing methods, in particular methods that allow study of source-resolved electroencephalographic (EEG) dynamics during walking (Gwin et al., 2010; Gramann et al., 2011; Wagner et al., 2012; Seeber et al., 2015) using a concurrent brain and body-movement imaging approach termed Mobile Brain/Body Imaging by Makeig et al. (2009a). EEG imaging allows investigation of the precise temporal dynamics of cortical brain processes time locked to behavioral measures including characteristics of single steps. Adopting this approach, we recently provided direct evidence for cortical top-down inhibitory control in step adaptation (Wagner et al., 2016). Participants were required to walk on a treadmill in time with a steady auditory tone sequence and then to adapt their step rate and length to occasional shifts in tempo of the pacing tones (i.e., in response to shifts to a faster or slower tempo). We observed that step adaptation in this paradigm was related to an increase in (15-20 Hz) beta band power localized in right dorsolateral prefrontal cortex (rDLPFC) (Wagner et al., 2016). The similarity of these features (right lateralized frontal beta power) to activity during top-down inhibitory control of finger press responses obtained from electrocorticographic (ECoG) (Swann et al., 2009; Wessel et al., 2013) and source-resolved EEG data (Wagner et al., 2018) is suggestive of a similar process.

Potocanac et al. (2015) showed that when requiring occasional steps over obstacles, larger demands on motor inhibition induced by a secondary task (Stroop task) during walking produced more step response performance failures. Haefeli et al., (2011) showed larger average event-related potentials (ERP) over frontal brain areas following auditory cues signalling an upcoming obstacle that participants needed to step over. De Sanctis et al. (2014), measuring EEG in a dual-task walking paradigm (a so-called ‘Go-NoGo’ task) requiring response inhibition, reported the involvement of a inhibitory cortical control network. They also showed that elderly participants were less able to flexibly allocate resources of this inhibitory network between the walking and cognitive tasks (Malcolm et al., 2015), further supporting the role of top-down inhibitory control in gait adaptation.

A crucial part of motor inhibition is recognizing stimuli that signal the need to inhibit or adjust motor responses, e.g., steps during walking. These events often occur suddenly and unexpectedly, such as the appearance of an approaching car or dog or a barely visible patch of ice. Brain dynamics supporting performance self-monitoring have been studied intensively in humans using EEG and functional magnetic resonance imaging (fMRI). One of the EEG signatures of performance monitoring in response to events signaling the need to adjust motor response plans, are error-related ERP features (error-ERPs). Error-ERPs are negative deflections in the EEG occurring near 100 ms after erroneous finger button-press responses -- termed the error-related negativity (ERN) (Falkenstein et al., 1990; Gehring et al., 1993) -- or near 250 ms following either negative feedback to incorrect button responses or autonomous machine-error responses -- the feedback-related negativity (FRN) (Miltner et al., 1997; Holroyd & Coles, 2002; Ferrez & Millàn, 2008; Zander & Jatzev, 2012; Zander et al., 2016). These error-related potentials can be detected in single trials (as reviewed in Charaviagga et al., 2014). The ERN and FRN are assumed to be functionally equivalent (Holroyd and Coles, 2002; Miltner et al., 1997) as source-resolved EEG studies (Dehaene et al., 1994; Ullsperger & von Cramon, 2001; Debener et al., 2005a, 2005b; Gentsch et al., 2009; Gruendler et al., 2011; Zander et al., 2016) have identified the same neural generator for these error-related potentials in the posterior medial frontal cortex (pMFC). FMRI studies (Ridderinkhof et al., 2004) have also identified an activity increase in pMFC associated with error processing.

The dominant current view, informed by both EEG and fMRI studies, is that error processing is accomplished by a central performance monitoring system that signals needs for behavioral adjustment in the service of action outcome optimization as informed by ongoing reinforcement learning (Ridderinkhof et al., 2004; Ullsperger and von Cramon, 2004; Holroyd & Coles, 2002) and that fluctuates over time (Debener et al., 2005a). Studies using trial averages have shown that these signals can be modulated by the importance of errors in a given task as well as by subjective awareness of an error (for reviews see Taylor et al. 2007; Wessel, 2012; Chavarriaga et al., 2014). Furthermore, behavioral adjustments associated with performance monitoring can, for instance, produce prolonged reaction times (RTs) on trials following errors, reflecting adoption of more cautious response criterion (Rabbitt, 1966; Ridderinkhof et al., 2004). This view is supported by fMRI results showing that larger blood oxygen level-dependent (BOLD) activity in pMFC following a performance error predicts slower, more careful responding (known as post-error slowing) in the next trial (Garavan et al., 2002; Kerns et al., 2004). In a simultaneous EEG-fMRI study Debener et al. (2005a) showed that trial-to-trial variation of the amplitude of both the independent component analysis (ICA) source-resolved error-ERP and of the ensuing pMFC BOLD signal response predicted the extent of RT slowing on the proceeding trial.

Here we aimed to test whether error-related brain dynamics in pMFC are involved in a dynamic motor task such as gait adaptation, and whether these error-related processes can predict performance adaptation on a trial-by-trial basis. ERPs are derived by averaging EEG signals across trials time-locked to a set of events that are assumed to evoke the same response. ICA (Makeig et al., 1996, 2002) may be applied to the continuous or concatenated trial data to isolate the brain effective sources contributing unique information to the scalp data, as well as non-brain (artifact) sources whose projections to the same electrodes are thereby separated from the brain effective source contributions. ICA is a statistical blind source separation technique that improves signal-to-noise ratio of measures of source dynamics (relative to closely-related scalp channel measures) and facilitates identification of single-trial EEG activity features linked to behavior and cognition more effectively than equivalent scalp channel-based measures (Makeig et al., 2002, 2004; Debener et al., 2005a; Onton & Makeig, 2006; Lenartowicz et al., 2014; Rissling et al., 2014).

To examine whether an error-ERP-like process may index cortical executive control processes during gait adaptation, we analyzed EEG data from an auditory pacing study using ICA and regression analysis (Wagner et al., 2016). Use of an auditory pacing stimulus stream, including infrequent tempo shifts, has been recommended to identify deficits and train improvement in gait adaptation in the elderly and parkinson’s patients (for reviews see Lim et al., 2005; Nombela et al., 2013; Stergiou et al., 2016; Ghai et al., 2018). In our paradigm participants walking on a treadmill moving at a steady rate were required to step in time to an auditory step cue tone sequence and then to adapt their step length (and, thereby, rate) to occasional shifts in the tempo of the cue stimuli (i.e., following shifts to a faster or slower tempo).

First, we expected to detect a negative deflection in the EEG, source localized to posterior frontomedian cortex, possibly 250 ms after tempo shift cues indicating a step tempo change to participants (similar to the FRN latency). Second, if an error-ERP negativity indeed reflects performance monitoring during walking, trial-to-trial variations of its ICA source-resolved amplitude should predict behavioral change in the ongoing and subsequent adaptation steps. Third, we aimed to test whether single trial error-ERPs would vary with the size of the cueing deviation (expressed as the time-period between expected and actual cue) indicating a step tempo change to participants. If true this would indicate that error-ERPs encode the degree of cueing deviation which may translate to the needed degree of behavioral adjustment.

2. Methods

2.1. Participants

Twenty healthy volunteers with no neurological or motor deficits participated in this study. The data of two subjects were excluded because of heavy EEG artifact. The remaining data of 18 subjects (10 males and 8 females, 22–35 years of age; mean 29.1 years, SD 2.7 years) were used in the analysis. All participants were right handed. Prior studies showed that footedness follows handedness in right handers, although not consistently so in left handers (Peters & Durding, 1979). The experiment was performed at Graz University of Technology, Austria. The experimental procedures were approved by the human ethics committee of the Medical University Graz. Each subject gave informed consent before the experiment.

2.2. Experimental design and procedure

2.2.1. Training

To become familiar with the treadmill, participants walked on the treadmill for 2–3 min before starting the experimental procedure. For a picture of the experimental setup see Wagner et al. (2016). During practice, we determined the belt speed for each participant in the experiment by asking participants to adapt the belt speed to their most comfortable walking speed. Selected belt speeds ranged from 3.0 to 3.7 km/h, and were held fixed throughout the rest of the experiment. Then, for about 5 min, participants practiced stepping on the treadmill in sync with a train of auditory cue tones to familiarize themselves with the task. Before beginning the experiment, we made sure the participant understood the task and had reached an acceptable level of performance, meaning that they appropriately adapted their steps to step-advance and step-delay pacing signal tempo shifts by shortening or lengthening their steps so as to synchronize to the new pacing tempo.

2.2.2. Trial structure

We elicited gait adaptations in participants during treadmill walking by including infrequent tempo shift challenges in the auditory pacing stream (Wagner et al., 2016). In each trial (Figure 1), participants first walked at their self-selected comfortable pace without auditory cueing for 10 s, after which a train of auditory cue tones was delivered via in-ear headphones at a tempo matching their then-current step tempo computed as the mean (heel strike to heel strike) step onset asynchrony (SOA) across their 6 most recent non-cued steps. The cue sequence was an alternating series of high and low tones presented so as to match the participant's alternating right and left heel strikes; high/low tone assignment to left/right or right/left steps, respectively, was randomized over subjects. Participants were asked to attempt to synchronize their heel strikes to the cue tones.

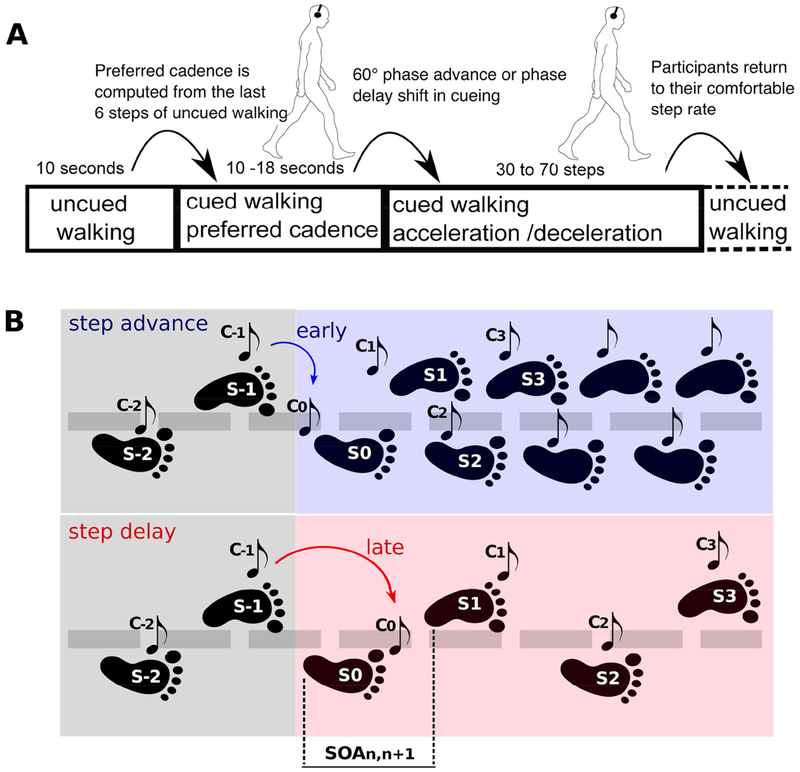
Figure 1. Experimental paradigm.

A. Throughout the session, treadmill speed remained fixed at a rate deemed comfortable by the participant. During each approximately minute-long trial, participants first walked for ~10 sec without auditory cues, then walked for 10–18 sec while attempting to synchronize their foot falls to brief cue tones delivered at their then-prevailing step rate and phase. Thereafter, beginning at a right heel strike (S₀), a sudden tempo shift occurred in the pacing cue sequence, the first tone indicating the new tempo by being early or late relative to the participant’s heel strike (S₀). In response, participants were instructed to adapt their step phase (percent latency difference from cue tone onsets), and step rate or step-onset asynchrony (SOA) as quickly as possible, so as to again synchronize their steps to the ensuing cue tones delivered at the new tempo. To do this, the constant pace of the treadmill movement required that they adjust their step length appropriately. After 30–70 steps synchronized to the auditory cues at the new preferred tempo, the next trial began immediately, beginning again with 10 sec of uncued walking during which participants were asked to return to their most comfortable (preferred) step rate. B. Snapshot of events during tempo shifts in step advance (blue background) and step delay (red background) conditions, showing schematic steps S₋₂ to S₃ and cues C₋₂ to C₃ around tempo shifts signaled by the timing of C₀. The tempo shift always occurred relative to a right step (S₀), the first deviant tone (C₀) indicating the new tempo by being early (e.g., on average 47 ms before S₀ in step-advance trials) or late (e.g., on average 165 ms after S₀ in step-delay trials). Distance between heel strikes represent SOAs -- i.e. the distance between S₁ and S₂ represents SOA_1,2.

While walking at the preferred cadence, auditory cues arrived at regular intervals, thus building an expectation of when the next cue would occur. After 10–18 s of auditory cued walking, the tempo of the cue train was suddenly increased (‘step-advance’ perturbation) or decreased (‘step-delay’ perturbation) by one-sixth of a step cycle, plus a random ≤±25 ms jitter, beginning with a tone cueing a right heel strike (as in Bank et al., 2011). When a step-advance or step-delay perturbation occurred, the first cue at the new tempo would thus seem to the walker to arrive either ‘too early’ (in step-advance) or ‘too late’ (step-delay). Participants were instructed to adjust their heel strike timing as quickly as possible so as to synchronize their heel strikes to the tone cues now arriving at the new pacing tempo. This new tempo was then maintained for 30-70 steps (see Figure 1). Since the treadmill moved at a steady speed throughout the experiment, step size or length and step duration were strictly proportional. Participants thus had to implement gait adjustments in two directions: either by producing (in step-delay trials) one-sixth longer (and, thus, slower) steps, or (in step-advance trials) one-sixth shorter (thus, more rapid) steps. After 30–70 steps at the new stepping rate, the next trial began immediately, again with uncued walking, during which participants were instructed to return to their most comfortable step length and tempo.

A total of 60 step-advance and 60 step-delay trials were conducted in 10 blocks of 12 trials, each comprised of 6 step-advance and 6 step-delay trials presented in random order. Between blocks, when asked for by participants 5-min breaks were given during which participants remained standing on the treadmill.

2.3. Data acquisition

Seven 16-channel amplifiers (g.tec gmBH, Graz) were combined so as to record EEG data from 108 electrode channels in the ‘5% International 10/20 System’ (EasyCap) (Oostenveld & Praamstra, 2002). Electrode locations that extended below the conventional 10–20 System layout included F9, FT9, F10, FT10, P9, PO9, P10, PO10, I1, Iz and I2. Reference and ground electrodes were placed on the left and right mastoids, respectively. All electrode impedances were brought below 5 kΩ before recording. The EEG data were sampled at 512 Hz. Recording bandpass was 0.1 Hz to 256 Hz. Foot contacts with the treadmill were measured by mechanical foot switches placed over the calcaneus bone in each heel. These switches produced event markers for gait cycle heel-strike and heel-off events. To record the exact timing of the auditory cues, we recorded the auditory stimulation via digital input to one of the EEG amplifiers.

2.4. Behavioral data analysis

The latency deviation of cue C₀ was quantified as the ms difference between expected, Expected(C₀), and actual, C₀, cue onset times, normalized by dividing by the baseline cued step duration.

$$\Delta C_0=\mid C_0-\mathit{Expected}(C_0)∕(C_{-1}-C_{-2})\mid$$ (1)

We defined post-shift step duration relative to pre-shift step duration, by normalizing post-shift SOAs by a pre-shift baseline -- the mean SOA in the most recent 4 steps of walking at preferred pace. Post-shift SOAs were scaled by preferred walking speed by expressing them as ratio relative to the pre-shift baseline (see Figure 2).

$${\mathit{SOA}}_{n,n-1}\Leftarrow {\mathit{SOA}}_{n,n-1}∕\frac{1}{4}{\sum }_{k=-1}^{-4}{\mathit{SOA}}_{k,k-1}$$ (2)

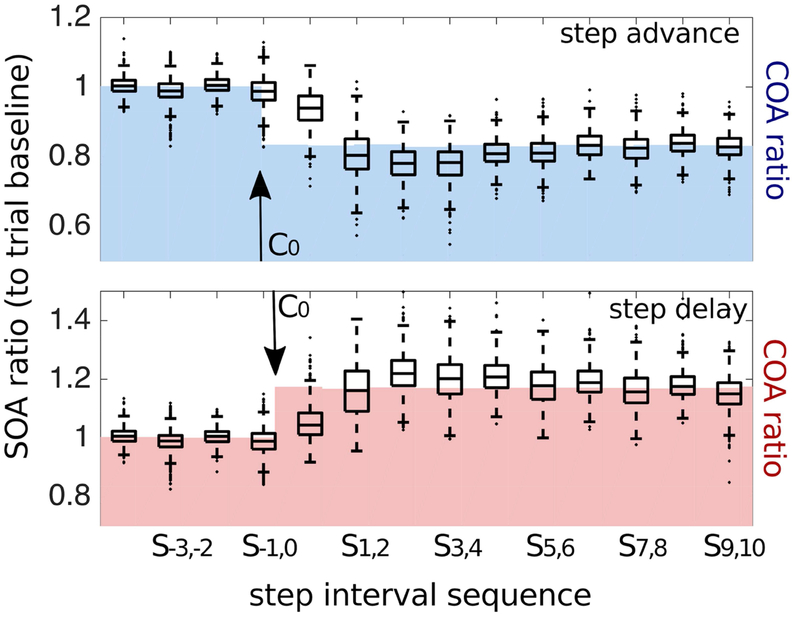
Figure 2. Behavioral results.

Boxplots show the distributions of single-trial step onset asynchronies (SOAs) across participants (in each box, the central black horizontal bar indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The vertical whiskers extend to the most extreme data points not considered outliers; outliers are plotted individually using black dots) in the two perturbation conditions (step-advance, upper panel; step-delay, lower panel), background blue- and red-shaded areas show the pacing cue onset asynchronies (COAs). SOA values are expressed as ratio change from trial pre-shift baseline SOA. Offsets of COA shifts (vertical arrows) symbolize that in step delay, cue C₀ follows S₀ while in step advance, cue C₀ on average slightly precedes S₀.

The values of k here represent heel strikes [−4 to −1] before the tempo shift, the values of n the heel strikes following the tempo shift. For more extensive analysis of the behavioral measures, see Wagner et al. (2016).

2.5. EEG data analysis

EEG data analysis was performed using custom scripts written in MATLAB 2014a (The Mathworks, Inc., Natick, Massachusetts, USA) incorporating functions from EEGLAB v14.0b (Delorme & Makeig, 2004; sccn.ucsd.edu/eeglab). In Wagner et al. (2012, 2014), we showed that artifact contamination of the EEG during upright walking can be separated from the brain source data using infomax Independent Component Analysis (ICA) (see also, Onton et al., 2006; Gwin et al., 2010). The preprocessing of the data here was the same as reported in Wagner et al. (2016).

The EEG data were high-pass filtered above 1 Hz (using a zero-phase FIR filter, order 7,500) to minimize slow drifts, and low-pass filtered below 200 Hz (zero-phase FIR filter, order 36). EEG channels with prominent artifacts were identified by visual inspection and removed. On average, 106 channels per participant (SD ±2.2; range 102–108) remained for analysis. The EEG data were then re-referenced to common average reference. After visually rejecting strong artifact periods in the continuous EEG, the data were partitioned into 0.5-s epochs; those epochs containing values exceeding the absolute mean value across data segments by ±5 SD were rejected from further processing. On average, 45 post-shift steps per condition (80% of each participant's step and EEG data) remained for analysis (SD ±11%; range 71%–89%).

Next, for each subject the accepted trials were concatenated in the time dimension and decomposed using Adaptive Mixture ICA (AMICA) (Palmer et al., 2006, 2008), based on the assumed temporal near-independence of the effective (brain and non-brain) EEG sources (Makeig et al., 2002, 2004). AMICA is a highly effective ICA approach for EEG data decomposition (Delorme et al., 2012) and can be viewed as a generalization of Infomax ICA (Bell & Sejnowski, 1995; Makeig et al., 1996) and multiple-mixture (Lee et al., 1999; Lewicki & Sejnowski, 2000) ICA approaches.

Using a standard (MNI) three-shell boundary element head model (BEM) implemented in the DIPFIT toolbox in EEGLAB, we calculated a best-fitting single equivalent current dipole matched to the scalp projection of each independent component (IC) source (Oostenveld & Oostendorp, 2002; Delorme et al., 2012). This method lies in the approximation of spatially coherent electrical activity within a small patch of the cortex as an equivalent dipole, which has long been shown to be a useful model (see Scherg, 1990) when and if the scalp map associated with the process of interest has a dipolar form (i.e., fits the projection of a single equivalent dipole). Recent evidence provides support for the assumption that many maximally independent EEG components separated by ICA decomposition are volume-conducted projections of partially-synchronous local cortical field activity within single compact cortical domains (Delorme et al, 2012).

We first visually inspected the remaining IC scalp maps, their event-locked time courses and mean power spectra to identify ICs related to non-brain artifact sources (eye movement and scalp/neck muscle artifacts), and de-selected them for further analysis. We then retained those remaining ICs for further analysis for which the equivalent model dipole was located within the brain volume and for which the projected scalp map of the equivalent current dipole accounted for more than 90% of variance of the model-equivalent IC scalp map. We chose the 10% residual variance threshold as a conservative value based on Artoni et al.’s (2014) result showing that components whose dipole explains at least 85% of variance of the scalp projection are reliable over bootstrap ICA decompositions of the data. Explained variance, here used as a measure of dipolarity, has been shown to index, on average, the quality of the independent component decomposition (Delorme et al., 2012). We considered the thus-selected ICs as ‘brain effective sources.’

2.6. Cortical IC cluster analysis

The above steps gave a variable number of brain effective source ICs per participant (typically 10 to 15). To identify similar ICs across participants we used k-means clustering. To this purpose, for each brain effective source IC, its position in a Cartesian space coding IC equivalent dipole locations, scalp maps, and (0-400 ms) ERP time courses (Makeig et al., 2002) was computed. Using principal component analysis (PCA), the scalp map and ERP measure vectors were reduced to 10 principal dimensions; equivalent dipole locations inherently have three dimensions. The dimensionally reduced feature vectors were then weighted for subsequent clustering: equivalent dipole location weight, 15; scalp map weight, 3; ERP weight, 5. The three feature vectors for each IC were then concatenated, and the resulting length-23 aggregated feature vector was further reduced to 10 principal components. The dimensionality reduction of this aggregated feature vector is necessary to avoid the “curse of dimensionality” in the k-means algorithm (Bellman, 1961, Steinbach et al., 2004). The k-means algorithm used then the dimensionally reduced aggregated feature vector to group the ICs into 15 clusters. ICs whose locations in the measure space were more than 5 SDs from the obtained cluster centroids were identified and removed from clustering. Only the 9 clusters including ICs from more than half of the participants are reported here. These consisted of two lateral frontal IC source clusters and two in lateral parietal areas, one cluster in left temporal cortex, one in/near left central sulcus, and three in midline cortex (frontal, central, occipital).

Some clusters included two or more ICs from the same subject. We reduced these subjects’ cluster contributions by removing from the cluster their IC(s) furthest from the cluster centroid in equivalent dipole location. Each participant contributed to at least 5 of the 9 selected clusters; only one of the 9 clusters (localized to right prefrontal cortex) included a source from all 18 participants, There are several possible reasons why this was the case. Possibly ICA decomposition and/or the IC clustering procedure might not have been able to resolve or properly group their brain sources because of subject differences in ERP appearance, channel numbers and/or locations, and/or data quantity. Else the presence of a larger number of spatially non-stereotyped artifact in some subjects may have reduced the number of data degrees of freedom available to identify brain effective source processes. Finally, the possibility that ICs “missing” from a cluster index actual inter-subject differences in cortical topography and/or dynamics cannot be rejected out of hand (see Onton et al., 2005).

2.7. Event-related potential analysis

We analyzed time courses of ERP averages time-locked to the presentation of the first latency-shifted cue tone C₀ in each trial. For this purpose the data were segmented into 2.3-sec time epochs spanning the period −0.5 s before to 1.8 s after each C₀ onset. These epochs were then averaged separately for step-advance and step-delay conditions (see Figure 3B). Here, we were interested in comparing the ERPs in this experiment to the ERP peak described in literature as the FRN, a negative deflection peaking at around 250 ms after an error or deviant event, characterized by a radial central topography and pMFC localization (Holroyd & Coles, 2002 Ullsperger et al., 2014; Debener et al., 2005a, 2005b; Miltner et al., 1997; Holroyd & Coles, 2002; Ferrez & Millán, 2008; Zander & Jatzev, 2012; Zander et al., 2016).

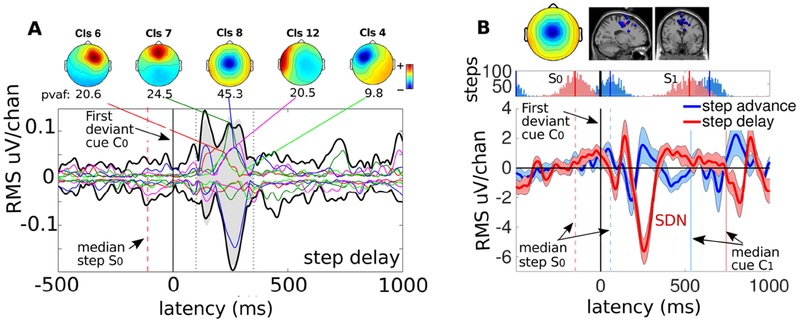
Figure 3. Source cluster contributions to ERPs time locked to the first latency-perturbed cue presentation in step-delay trials and average pMFC cluster ERPs.

A. (colored traces) ERP envelopes for the 5 largest-contributing in the 100-350 ms time range (shaded, between the dotted lines) source clusters (cluster-mean scalp maps shown) versus the ‘sum of all 9 clusters’ ERP envelope (black traces) for step delay trials. B. pMFC cluster-mean scalp map and equivalent dipole locations, step latency trial histograms, and cluster-mean IC ERPs for step-delay (red line) and step-advance (blue line) shifts. Step-delay perturbations (only) show a prominent negative deflection peaking 250+ ms after C₀ onset, here referred to as the step-delay negativity (SDN), while step-advance perturbation include a much smaller and slightly earlier negative deflection. Tinted ERP envelopes indicate confidence intervals (±3 standard errors). The black vertical line at zero marks the onset of the first deviant cue tone (C₀); dashed vertical lines represent the median latencies of the nearest heel strike (red: step-delay, blue: step-advance; note heel strike histograms above); ensuing solid vertical lines represent median times of occurrence of the next cue tone onset. IC activities are scaled by RMS of the column corresponding to the IC of the inverse ICA weight matrix (the IC scalp map).

We therefore looked for a condition and IC cluster whose C₀-locked ERP exhibited similar characteristics. For this purpose we evaluated IC cluster contributions to the scalp channel ERP grand mean time courses time locked to C₀ (Makeig et al., 2002; Lee et al., 2015). We measured the source contributions of each IC cluster to the scalp signals in terms of percent variance accounted for (pvaf) to find the clusters of brain source ICs that explained, in total, at least 80% of the variance accounted for in the resulting envelope of the grand mean ERP (see Figure 3A).

We selected for further analysis the largest contributor to the grand mean step-delay scalp ERP, the pMFC cluster composed of ICs displaying scalp maps resembling the typical frontocentral radial ERN topography and a large negative deflection 200-300 ms after the first deviant cue onset (C₀), possibly reflecting the contribution of the neural correlate of performance monitoring to the scalp EEG. Below we will refer to this negative deflection as the step-cue delay negativity (SDN).

To extract one value for ERP amplitude per trial, the IC activities were scaled by RMS of the column corresponding to the IC of the inverse ICA weight matrix (the IC scalp map). The units of the backprojection are then RMS μV across the scalp channels (RMS μV/chan). The data were then low pass filtered below 20 Hz with an order-4 Butterworth IIR filter. We then computed the dot product, < SDN,μ_SDN >, between each single-trial time course (SDN) and the cluster-mean ERP (μ_SDN) in a latency window 100-350 ms following C₀ cue onset. The dot products here represent projections of each single trial activity waveform onto a common response vector (here μ_SDN), and can be interpreted as a one-dimensional measure of the divergence of the two vectors. This dot product estimates (1) the degree to which the EEG time course in the single trial resembles the grand mean ‘template’ ERP, and (2) the strength with which the template ERP pattern is expressed.

2.8. Visualizing trial-by-trial SDN variability

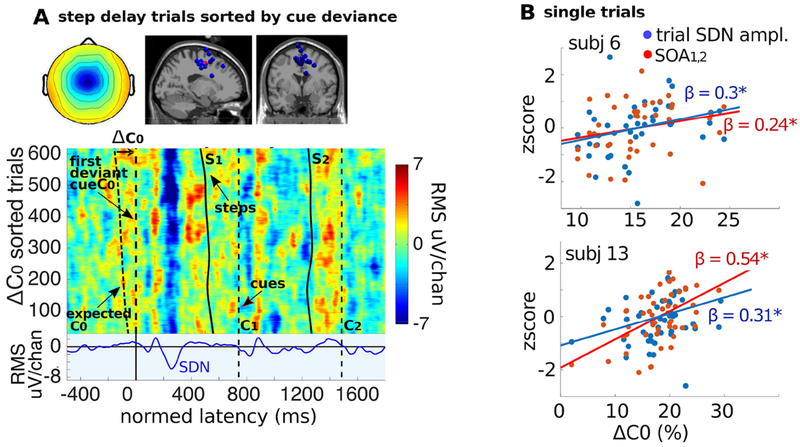
To visualize the relationships between the cue timing error, SDN amplitude, and adaptation step length, we generated trial-by-trial ERP-image plots of IC activities time-locked to C₀ cues signalling step-delay perturbations. ERP-image presentation allowed relationships between cue error, ERP features, and adaptation step length to be clearly visualized. For these plots, we first scaled IC activities by RMS of the column (corresponding to the IC) of the inverse ICA weight matrix and then low pass filtered the data below 20 Hz with an order 4 Butterworth IIR filter. We then time-warped the single-trial IC activities using the EEGLAB function timewarp() which uses piecewise linear interpolation to adjust the latencies of specified events occurring in each epoch to their median latencies, here cues C₁ and C₂ following the tempo-shift cue (C₀). This procedure aligned the plotted latencies across trials at cue onsets C₁ and C₂ as well as at the time-locking cue onset C₀. We then first sorted the time-warped single trials by the normalized duration of the major adaptation steps SOA_0,1 and SOA_1,2 (separate ERP-images were generated for SOA_0,1 and SOA_1,2 sorting and for step advance and step delay trials). After sorting, the images were smoothed over adjacent trials with a 30-trial moving average (see Figure 4A for step delay trials sorted by SOA_1,2). Next, we sorted the same time-warped trials by the size of the initial auditory timing deviation ΔC₀ (eq 1 above). The random [−25, 25] ms trial-to-trial jitter in C₀ latency ensured that the size of the auditory cueing deviation at tempo shift differed slightly over trials, allowing us to explore its relationship to the amplitude of the following SDN. Again the images were smoothed (vertically) across the sorted trials using a 30-trial moving average (see Figure 5A for step delay trials).

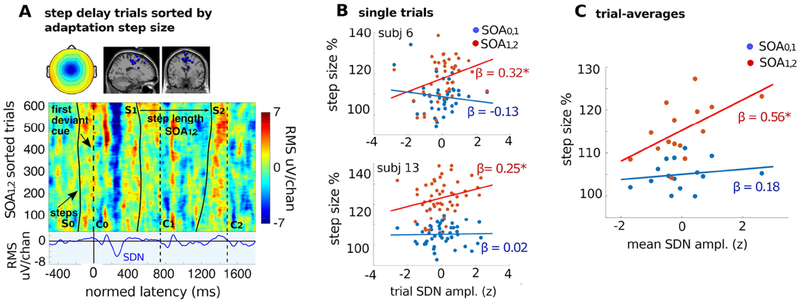
Figure 4. Single-trial ERPs sorted by adaptation step size, plus within- and across-subjects regressions on SDN magnitude.

A. Top panel: pMFC cluster-mean scalp map and cluster IC equivalent dipole locations. Middle panel: For illustration, single-trial ERPs time locked to C₀ were first time warped to fix latencies of C₁ and C₂ across trials (see Methods) then pooled across pMFC-cluster ICs and sorted by adaptation step size (SOA_1,2). Blue indicates negative activation; red, positive activation (green: 0). Dashed black vertical lines represent cue onsets; solid black traces represent heel strikes of adaptation steps S₀ through S₂. Upper trials in which the participant made a larger (SOA_1,2) adaptation step exhibit a stronger SDN near 250 ms. Bottom panel: The cluster-mean ERP. B. Scatterplots of single trials for two example pMFC cluster ICs (subject 6 - 41 trials and subject 13 - 54 trials) plotting trial-by-trial relationships between SDN magnitude and size of adaptation steps SOA_0,1 (blue dots) and SOA_1,2 (red dots). As seen in the ERP-image plot (A), the size of adaptation step SOA_1,2 is positively correlated with SDN magnitude. C. Scatter plots showing, for all cluster ICs, the relationship between IC trial-mean SDN magnitude and step size for adaptation steps SOA_0,1 (blue dots) and SOA_1,2 (red dots). Note the positive correlation between SOA_1,2 and trial-mean SDN magnitude (red regression line). Asterisks indicate significance (p<0.05).

Figure 5. Single-trial step-delay responses to C₀ and regressions on ΔC₀.

A. Top row: Cluster-mean scalp map and cluster-IC equivalent dipole locations. Below: After normalization by time warping (as in Fig. 4), the single-trial ERPs were pooled across all ICs in the pMFC cluster and sorted by the normalized difference (ΔC₀) between C₀ and expected C₀ latencies to make an ERP-image plot (vertical smoothing, 30 trials). Cool colors (blue) indicate negative activation values, warm colors (yellow to red) positive activation values. Dashed black vertical lines represent cue tones (C₀ to C₂). The leftmost dashed black trace represents the latency at which cue C₀ was expected to occur. Solid black traces represent heel strike latencies for steps S₁ and S₂. In upper trials with relatively large ΔC₀ the negative (SDN) deflection near 250 ms is stronger. The bottom panel shows the cluster-mean ERP. B. The effects of ΔC₀ on SDN magnitude and on SOA_1,2 adaptation-step size. Scatterplots for two of the 15 pMFC cluster ICs (subject 6 - 41 trials and subject 13 - 54 trials) showing relationships between ΔC₀ (on the x-axis), and z-scored SDN magnitude (blue dots) as well as z-scored adaptation-step size SOA_1,2 (red dots). Asterisks indicate significance (p<0.05).

2.9. Regression analysis

Regression analyses were computed on the 15 ICs in the pMFC cluster. We first tested the relationship between SDN amplitude and the lengths of the two first adaptation step durations (SOA_0,1 and SOA_1,2) following cue tempo perturbations. These were the steps in which most of the step adaptation to the new tempo was performed. To do this, we computed two multivariate regressions on these step lengths:

$$({\mathit{SOA}}_{1,2},{\mathit{SOA}}_{0,1})=\alpha +\beta \times <\mathit{SDN},{\mu }_{\mathit{SDN}}>$$ (3)

• 1)For each IC separately we computed regression to predict step sizes based on SDN magnitude (SDN,μ_SDN >) in single trials, giving two beta coefficients (β) for each IC. We then computed t-tests over these β coefficients for SOA_0,1 and SOA_1,2 separately, assuming that the null hypothesis could be rejected if these were significantly different from a distribution with zero mean (see Figure 4B).
• 2)We also computed regression in the 15 cluster-IC trial-average ERPs to predict step sizes based on SDN magnitude. In this case measures of SDN magnitude were computed as dot products between each cluster-IC trial-average ERP and the grand cluster-mean template ERP, again in the latency window 100-350 ms following C₀ (see Figure 4C). Single trial SOA_0,1 and SOA_1,2 were normalized as described in section 2.4 and then averaged over trials for each subject.

Since multivariate single-trial regressions and trial-average regressions following step-delay perturbations were significant for SOA_1,2 but not for SOA_0,1, and regressions for step-advance perturbations did not reach significance, we concentrated further analysis on SOA_1,2 following step-delay perturbations.

Above, we investigated how trial-to-trial variability in SDN magnitude predicts step adaptation. But what prompts or determines SDN variability? To explore this question, we investigated quantitatively whether and how trial-to-trial variability in the size of the initial auditory timing deviation (ΔC₀) at the tempo shift relates to ensuing SDN magnitude. The random [−25, 25] ms trial-to-trial jitter in C₀ latency ensured that the size of the auditory cueing deviation at tempo shift differed slightly over trials, allowing us to explore its relationship to the magnitude of the following SDN.

• 3)
  The multivariate regression

  $$(<\mathit{SDN},{\mu }_{\mathit{SDN}}>,{\mathit{SOA}}_{1,2})=\alpha +\beta \times \Delta C_0$$ (4)

  examined, within subjects / cluster ICs, the contribution of C₀ timing-error magnitude, in single trials, to subsequent SDN magnitude and adaptation step size (see Figure 5B).
• 4)
  To disentangle the joint contributions of ΔC₀ and SDN to adaptation step size, we also performed within-subjects multiple regression,

  $${\mathit{SOA}}_{1,2}=\alpha +{\beta }_1\times <\mathit{SDN},{\mu }_{\mathit{SDN}}>+{\beta }_2\times \Delta C_0$$ (5)

  to predict the behavioral adaptation step size in single trials.

P-values were corrected for multiple comparisons using false discovery rate (Benjamini & Yekutieli, 2001) and the Benjamini-Hochberg Procedure (Benjamini & Hochberg, 1995) that reduces Type 1 error (false positives). Multiple comparison correction was performed over the number of p-values we obtained from the regressions and t-tests over β coefficients.

2.10. On the cortical origin of the SDN

Several recent studies (Castermans et al., 2014; Kline et al., 2015; Snyder et al, 2015) found artifactual contamination of EEG data recorded during upright walking at frequencies from 1 to 150 Hz. Castermans et al. (2014) compared accelerometer signals recorded from the head and EEG data recorded during walking and found similar time/frequency properties in those signals. Kline et al. (2015) and Snyder et al. (2015) blocked electrophysiological signals by using a silicone swim cap as a non-conductive layer under a standard EEG cap to record pure movement artifacts during walking. They observed movement artifacts, depending on walking speed and electrode location, had energy from 1 Hz to 150 Hz, but also showed that source separation with ICA and subsequent single equivalent current dipole localization located 99% of the obtained pure artifact outside the head or lacking dipolar characteristics (residual variance >15%). Only 1% of ICs had equivalent dipoles localized inside the brain with residual variance <15%. However these ICs had scalp maps, time courses, power spectra, and time-frequency changes typical of movement artifacts. Snyder et al., (2015) thus shows that movement artifacts induce broadband frequency changes in signals recorded at scalp electrodes, and that these non-brain artifacts can be reliably identified and separated from brain source signals using ICA.

An additional source of artifact contamination in EEG signals recorded during movement are neck and scalp muscle activations (Gramann et al., 2010; Gwin et al., 2010; Seeber et al., 2014). Scalp EMG artifacts appear across frequencies above 20 Hz (Muthukumaraswamy et al., 2013; Castermans et al., 2014). By contrast, electrocortical oscillations relative to motor or cognitive processing have been shown to decrease or synchronize in narrow frequency bands, including μ (7–12 Hz) and β (15–30 Hz) during restricted lower limb movements (Pfurtscheller et al., 1997; Crone et al., 1998; Miller, 2007; Muller-Putz et al., 2007) and walking (Wagner et al., 2012, 2014; Severens et al., 2012; Seeber et al., 2014). Broadband high-frequency power changes (above 60Hz within and beyond the γ band) have been suggested to play a distinct role in cortical processing (Onton and Makeig, 2009; Miller et al., 2014). Because mechanical artifacts biological noise, and cortical signals, possess distinct properties in waveform, frequency range, and spatial distribution, proper application of signal processing methods allows separation of these sources (Makeig et al., 1996; Gwin et al., 2010; Wagner et al., 2012; Seeber et al., 2014, 2015; Snyder et al., 2015).

Previous work using ICA has shown the successful removal of movement artifacts during walking for the analysis of event-related potentials (Gramann et al., 2010; DeSanctis et al., 2014; Malcolm et al., 2015). In our study, the SDN cannot be caused by movement artifacts resulting from a step with more impact because: First, in step delay perturbations at time S₀ participants are not yet aware of a tempo shift since during preferred walking they always step in time slightly before the cue (see 3.1. Behavioral Results). Second, in Wagner et al., (2016) we plotted ERPs locked to C₀ and to S₀ and showed that the stimulus-locked SDN (to C₀) is larger than the step-locked negativity. If the SDN would be related to a movement artefact it should be larger and more prominent when locked to the step (S₀). Third, we also provide baseline corrected time frequency transforms - event related spectral perturbation images (ERSPs, Makeig, 1993) (see Supp. Fig. S3C) for the pMFC cluster, and show a (4-7 Hz) theta power increase at the time of the SDN, as has been shown in many studies on error processing (Luu et al., 2004; Cavanagh et al., 2009). Cluster pMFC ERSPs display no broadband power changes which are typical of movement artifacts (see Castermans et al., 2014; Kline et al., 2015; Snyder et al., 2015). We also provide ERP and ERSP images of a cluster related to movement artifacts, clearly showing typical spectral broadband power changes and a rhythmic ERP time course peaking after heel strikes (see Supp. Fig. S4). It is important to mention that all ICs contained in the movement artifact cluster had equivalent dipoles that explained less than 85% of their scalp projection, in line with Snyder et al.’s (2015) results (see above). We thus show that the SDN and pMFC cluster activity are clearly distinct from activity of typical movement artifact clusters.

3. Results

3.1. Behavioral Results

Participants walking on a treadmill had to adapt their steps following a change in tempo of an auditory step-timing cue sequence to a faster or slower tempo. Figure 1 shows a schematic of the task paradigm, as well as a schematic image displaying the timing of the steps and cues around the time shift. Figure 2 presents a plot of the normalized SOA ratios from step S₋₃, 3 steps before, to step S₁₀, 10 steps after S₀, the heel strike occurring nearest to the first tone implementing the cue-tempo shifts (C₀). This (S₀) was always a right heel strike, with respect to which the first deviant cue (C₀) arrived either unexpectedly early (before S₀ in step-advance trials) or unexpectedly late (after S₀ in step-delay trials).

The average SOA during preferred cadence walking was 637 ms. The cue tempo shifts, announced by a cue arriving 1/6 of the baseline step cycle before or after an expected cue onset, thus produced a mean deviation over participants of ± 106 ms, to which was added the random <±25 ms jitter.

During walking at the preferred cadence (e.g., during steps S₋₄ to S₋₁ before the shift), we observed that heel strikes consistently occurred ahead of the cues (mean difference −59 ms; SD ±43 ms). Thus, a ⅙-step cue delay unexpectedly shifted the time of occurence of C₀ to more distinctly follow heel strike S₀ (C₀ – S₀ = +165ms on average) while a ⅙-step cue advance shifted C₀ to occur slightly before S₀ (C₀ – S₀ = −47ms on average).

We were especially interested in the first two step intervals (SOA_0,1 and SOA_1,2) directly following S₀ -- in Figure 2 these are denoted as S_0,1 and S_1,2 -- as most of the gait tempo adaptation occurred in this period. Note in Figure 2 that by step SOA_1,2 participants, on average, had largely adapted their step timing to the new cue train and tempo (underlying blue and red area). Interestingly, attaining their baseline level of step-cue synchrony took much longer (see Wagner et al, 2016).

3.2. IC source cluster ERPs

We estimated the source contribution of IC clusters to the scalp signals in terms of percent variance accounted for (pvaf) (Lee et al., 2015). The envelopes of the summed scalp projections of selected IC clusters contributed to the prominent negative deflection occurring following step-delay shifts about 250 ms after the first deviant cue. Figure 3A, using EEGLAB function std_envtopo (Lee et al., 2015), visualizes the envelopes of the 5 largest component cluster projections; together, they explained 87% of the variance in the summed scalp ERP contributions of the 9 selected IC clusters in the step-delay condition.

Independent component cluster in pMFC comprised 15 ICs that exhibited a large contribution to the negative peak 200-300 ms after the first deviant cue, and had scalp maps resembling the typical frontocentral radial topography of the feedback-related negativity (FRN). The cluster localized in pMFC explained the largest part (45.3%) of the total variance in the 100-350 ms ERP latency window and of the circa 250-ms negative peak in particular, which we refer to here as the step-cue delay negativity (SDN). Since activity of the pMFC cluster may reflect performance monitoring, this cluster was selected for further analysis.

In the step-advance condition ERP there was no prominent SDN-like negative peak near 250 ms (Figure 3b), and the pMFC cluster explained only 23% of the (100-350 ms) ERP (Suppl. Fig. S1A).

3.3. SDN magnitude and step duration

A key prediction that can be derived from performance monitoring models is that physiological signatures of error monitoring should predict behavioral adjustments at the single-trial level. To address this, SDN magnitude was estimated for every trial by taking the dot product of the 20-Hz low-pass filtered IC single-trial signals in the 100-350 ms latency window with the cluster-mean ERP in the same window. We examined the relationship of the resulting trial-by-trial SDN magnitude estimates for each subject to their subsequent behavioral adjustment to the new cue tempo. Results indicate a clear relationship between SDN size and subsequent step length/duration adjustment.

Following step-delay perturbations, the trial-by-trial ERP magnitude was significantly related to the succeeding step (SOA_1,2) duration -- longer-duration steps were preceded by a larger single-trial SDN in the pMFC cluster ICs (β = 0.17; p = 0.004, eq. 3 above). Thus, activity variations in the brain performance monitoring system, as estimated by this trial-by-trial source-resolved EEG measure, significantly predicted rapid gait adaptation performance. Results from multiple regression on single trials (eq. 5) looking at independent contributions of ΔC₀ and SDN to SOA_1,2 show a significant effect of SDN on SOA_1,2 that is independent of ΔC₀ (see details in next paragraph). Regression across participants on trial-average SDN magnitude in the pMFC cluster showed the same significant relationship between SOA_1,2 step duration and SDN magnitude (β = 0.56; p = 0.02). The present analysis thus demonstrates that step size adaptation was driven by electrophysiological activity related to error processing in the pMFC. This was true only for SOA_1,2 -- SOA_0,1 duration was not significantly correlated with SDN magnitude, neither in single trials (β = 0.017; p = 0.72) nor in trial averages (β = 0.18; p = 0.5).

To visualize the relationships between the SDN complex and step length we generated an all trials ERP-image plot for step-delay perturbations (Figure 4A) by accumulating the trials for all the ICs in the pMFC cluster and sorting them by SOA_1,2 (for details see Methods). The ERP-image plot shows that, in ICs in the pMFC cluster, a larger negative deflection in the source-resolved EEG was followed by a larger step response SOA_1,2. To visualize the relationships between the ERP complex and step length, we plotted dot product values against step length with a least squares line for single trials within subject ICs (Figure 4B), and for the trial average across subject ICs (Figure 4C) for step-delay perturbations.

Multivariate regressions for effects on SDN magnitude of step-advance perturbations on the first adaptation step size SOA_0,1, either in single trials within IC (SOA_0,1: β = −0.10; p = 0.19; SOA_1,2: β = −0.13; p = 0.08) or in trial averages across ICs (SOA_0,1: β = −0.07; p = 0.8; SOA_1,2: β = −0.05; p = 0.9) did not reach significance.

3.4. Precursor of trial-to-trial variability in SDN magnitude

Trial-to-trial variability in the SDN was linked to the size of the ΔC₀ timing deviation. Multivariate regression (eq. 4 above) over single trials within subjects showed that the size of the C₀ timing shift significantly predicted both SDN magnitude (β = 0.10; p = 0.039) and subsequent SOA_1,2 adaptation step size (β = 0.43; p ≤ 0.001). To visualize the relationship between ΔC₀, SDN magnitude, and SOA_1,2 step size, we also plotted (Figure 5B) ΔC₀ in single trials against SDN magnitude and against SOA_1,2 adaptation step size (regression lines from eq. 4 above), for two example ICs contained in the pMFC cluster.

To visualize the relationships between ΔC₀ and SDN magnitude, we constructed a single trial ERP-image plot for step-delay perturbation trials (Figure 5A) by accumulating these trials for all the ICs in the pMFC cluster and sorting them by their ΔC₀ (see Methods for details). The [−25, 25] ms jitter added to the ⅙-step timing shift ensured that the size of the auditory cueing deviation ΔC₀at the tempo shift varied slightly across trials in each condition. The ERP-image plot shows that the negative SDN deflection was stronger in trials with larger ΔC₀.

To determine the relative contributions of ΔC₀, and SDN magnitude to SOA_1,2 step size, we also computed a multiple regression (eq. 5 above) on step-delay perturbation trials of pMFC cluster ICs. This multiple regression showed a strong relationship between cue latency deviation (ΔC₀) and adaptation step size (β = 0.42; p ≤ 0.001). The effect of SDN magnitude on adaptation step size was independent of the effect of the cue deviance (ΔC₀) itself (β = 0.13; p = 0.009).

4. Discussion

The present study demonstrates trial-by-trial event-related coupling between simultaneously recorded, source-resolved EEG dynamics and gait adaptation behavior in humans. Here, an EEG ‘step-cue delay negativity’ (SDN) was generated in or near posterior medial frontal cortex (pMFC), peaking about 250 ms after anomalous cue tone onsets that followed a heel strike in a steady-state treadmill walking condition -- rather than nearly coinciding with their heel strike, as the participant intended and firmly expected. We found that trial-by-trial SDN amplitude in this gait challenge task was linearly related to both the magnitude of the tempo shift cue deviation (ΔC₀), as well as to the adequacy and effectiveness of their subsequent (SOA_1,2) step lengthening to bring their steps back into near-synchrony with the (now slower-tempo) cue train.

Our finding here that post-SDN step adaptation in a treadmill walking task is predicted by trial-by-trial as well as by subject-average SDN amplitude has not been previously reported. However, in line with this result both single-trial (Debener et al., 2005) and trial-average (Gehring et al., 1993) amplitude of the error-related negativity (ERN) in the EEG after erroneous finger button-press responses predicts slower, more careful responding (known as post-error slowing) in the next trial. Consistent with performance-monitoring models summarized by Debener et al. (2005a), the size of the SDN here also appears to index the need to adjust the current motor plan.

Debener et al. (2005a) suggested that single-trial ERN amplitude indexes activation of pMFC neural circuits involved in adjusting subsequent motor plans (Debener et al., 2005a), and invasive recordings show that performance adjustments are preceded by increased firing rates of pMFC neurons (Shima & Tanji, 1998; Williams et al., 2004). We similarly suggest that SDN amplitude, both in single trials within subjects and in trial averages between subjects, indexes trial-by-trial fluctuations in the activity of brain performance monitoring circuits responsible for, here, recognizing the need for and planning step timing and length adjustments during walking.

The similarity in cortical origin of the SDN to that of the error-related negativity (ERN) produced just after a committed button press error (Falkenstein et al., 1990; Gehring et al., 1993; Debener et al., 2005a) as well as to that of the ‘feedback-related negativity’ (FRN) following negative feedback to a motor decision error (Miltner et al., 1997; Holroyd & Coles, 2002, Dehaene et al., 1994; Ullsperger & von Cramon, 2001; Debener et al., 2005a, 2005b; Gentsch et al., 2009; Gruendler et al., 2011; Zander et al., 2016), plus similarities in the polarity, duration, and latency of these three negative-going ERP features, suggest they all index activity in the same brain behavior monitoring and/or planning network.

4.1. Error processing predicts step adaptation

We found that performance monitoring as indexed by the SDN predicted the size of the subsequent adaptation step, in single trials (within subjects) as well as on average (across subjects). Larger negative deflections were associated with longer (SOA_1,2) adaptation step durations following delayed tones cueing the onset of the slower step-cue tempo. Thus, activity variations in the brain’s performance monitoring system, indexed by the pMFC source-resolved EEG negativity in single trials, significantly predicted gait adaptation.

Application of ICA spatial filtering allowed imaging of effective source-resolved, locally coherent cortical field activity reaching the scalp through spatial summation and volume conduction. The major effective source of the SDN, as revealed by ICA decomposition, thus revealed details of EEG source activity in single trials that proved to be functionally dispositive (compare to Makeig et al., 2002, 2004; Debener et al., 2005a; Onton et al., 2005). In the step-delay condition, a cluster of brain IC processes for 15 of the 18 subjects, compatible with an origin in pMFC, produced an SDN negativity that shared features of the ERN complex including scalp topography, equivalent dipole location and ERP morphology.

Step adaptation was measured by normalizing each step onset asynchrony (SOA) by the average pre-shift SOA (eq. 2). This proportional measure ensured that behavioral measures are not biased by the overall speed of walking or by inherently larger or smaller steps due to leg length of participants. We focused on the two step intervals (SOA_0,1 and SOA_1,2 in Fig. 1) that followed unexpected cue tempo shifts since those represented a large part of the step adaptation process. Our results demonstrate that SDN magnitude significantly predicted the size of the adaptation step (SOA_1,2) in step-delay trials. The first deviant cue (C₀) always arrived after a committed heel strike (S₀) in step-delay trials thus SOA_1,2 always succeeded the occurrence of C₀. Our results thus suggest that participants were only able to change the length of their succeeding step following the perception of C₀ but not their ongoing step during occurrence of C₀(see Figure 1B).

Previously a relationship between behavioral adjustments and error-related potentials (Gehring, 1993; Debener et al, 2005a, West et al., 2008; Schuch et al., 2007; Nunez et al., 2011) or mid-frontal theta power (Luu et al., 2004; Cavanagh et al., 2009) has been shown. Most of these studies have shown a slowing in reaction time in the trial subsequent to the error-related potential (Rabbit, 1966; Gehring et al., 1993; Debener et al., 2005a; Danielmeier et al., 2011; for detailed reviews see Danielmeier & Ullsperger, 2011; Ullsperger et al., 2014). Other studies have shown that ERN amplitude and related theta power predicts response accuracy in the next trial (Themanson et al., 2012; Carp et al., 2009; Cohen et al., 2013). However, these post-error adjustments have previously only been studied in tasks requiring one discrete movement per trial, not for tasks requiring a continuous motor action stream, and not in an adaptive motor task. Contrary to the previously shown ‘post-error slowing’ of reaction time, the relationship of the adaptation step to preceding SDN amplitude we report here was likely not due to post-error slowing, since slowing down one’s gait in the real world during overground walking would entail making smaller steps. Lengthening one’s stride on a treadmill instead requires increased effort from the beginning of the step to achieve a more successful advance toward step cue tempo adaptation. Thus, the behavioral step adjustment we found to be related to the SDN is likely due to a optimized behavioral adjustment following a larger error-related ERP feature.

It has been suggested that self-recognized motor errors recruit a frontobasal-ganglia network to interrupt ongoing motor representations (Wessel & Aron, 2017). When fast motor adaptation (within milliseconds) is required, this fast inhibitory control may help to disengage the current movement plan and implement a new motor plan. In fact, in the same gait adaptation task we have shown that a right frontal beta band increase involved in top-down inhibitory control in ECoG and EEG in a manual stop signal task (Swann et al., 2009; Wagner et al., 2018) is also involved in adaptive step shortening (here in step-advance trials, about 300 ms after the SDN) (Wagner et al., 2016). Generalizing these and other error-related EEG/ERP results, it is likely that the family of early fronto-central evoked and induced EEG features (ERN, FRN, SDN, etc.) index fast alarm signals providing evidence of need for motor plan and action adaptation.

Here we have shown that SDN magnitude significantly predicted subsequent adaptation step size following C₀ step-delay cue train perturbations -- though not following step-advance perturbations. Why this is the case is not entirely clear. The evoked responses to the step-advance and to the step-delay cue tones were rather different (Figure 3B), and the step-advance response did not contain an SDN-like peak. Further, the pMFC cluster only explained 23% of the variance of the artifact-cleaned step-advance scalp ERP between 100 ms and 350 ms (versus 45% for step delay). Negative-going deflections in the step-advance ERPs were notably smaller than for step delay, and weremore variable across participants in both timing and amplitude. This might be linked to details of C₀ timing in this paradigm. During step-advance perturbations, C₀ occurred just before the S₀ heel strike and much closer in time to S₀than during step-delay perturbation trials. Thus, it might be that in some cases the mis-timing of C₀ may not have been as perceptible or salient to the participant as during cue-delay trials.

Time-frequency transforms (see Suppl. Fig. 3C) show that following step-advance perturbations the oscillatory theta-band increase was much weaker than following step-delay perturbations, and occurred both after C₀ and again after C₁. This suggests that in some step-advance trials participants may not have perceived the timing deviation of C₀ and thus may have perceived C₁ as the first deviant cue. These differences in sensitivity for the detection of deviations in environmental demands may be explained by the fact that certain phases of the gait cycle may require increased attentional resources. Lajoie and colleagues (1993) showed that in a dual-task walking paradigm target detection response time increased during the single-support phase of the gait cycle (one foot in swing), compared to during double support (both feet planted). This suggests that the more critical balance demand during single support may thereby increase attentional demand (Lajoie et al., 1993). During step-advance trials deviant cues (C₀) onset occurred during single support (shortly before heel strike), while in step-delay trials C₀ onset occurred during double support (shortly after heel strike). Because of gait phase-specific variation in balance demand there may have been less attentional capacity to support C₀ deviance detection in step-advance trials, a difference possibly associated with a less distinct cue-locked pMFC cluster ERP. Recently several studies have suggested an important role of balance and stability dynamics during walking, with balance perturbations/adaptations producing source resolved EEG responses in frontal, parietal and motor areas of the brain (Sipp et al, 2013, Bruijn et al., 2015, Solis-Escalante et al., 2019). A paradigm in which the deviant cues were more evenly distributed through the gait cycle might give more information on this topic.

4.2. Trial-by-trial variability in SDN magnitude

Here, in step-delay trials SDN magnitude was predicted by the size of the prediction error (defined as ΔC₀, the difference between the expected and actual onset latencies of deviant cues). The larger the ΔC₀, the larger the SDN. The larger the SDN, the larger the ensuing SOA_1,2 step adaptation, thus allowing an interpretation of SDN as indexing the degree of intensity of action plan adaptation inferred from the cue timing disparity. SDN magnitude hereby significantly explained parts of the subsequent step lengthening (SOA_1,2) independently of the magnitude of the tempo shift cue deviation (ΔC₀).

Our results can be explained in terms of predictive coding theory (Hawkins & Blakeslee, 2007), which holds that predictions of future events are continuously generated by the brain, and that these are then continuously compared to subsequent sensory evidence. The brain evaluates the correctness of its predictions and actions using the results of these comparisons, providing a fundamental mechanism — the minimization of prediction error — to shape, maintain, and optimize behavior in the face of continual environmental change. The brain dopaminergic signaling system is assumed to be the carrier of the corresponding predictive signals. Deviations between predicted and perceived outcomes translate to changes of the dopaminergic input to the anterior cingulate cortex (Holroyd & Coles, 2002). Adaptation is implemented based on a weighted prediction-error signal, indicating a deviation of the perceived outcome from the expected outcome (in our case related to ΔC₀). More negative prediction errors (worse-than-expected outcomes) are proposed to be associated with larger EEG error-related potential features and stronger hemodynamic signal changes (Holroyd & Yeoung, 2012; Zander et al., 2016).

Previous studies have shown that error-related potentials can be modulated by the subjective awareness of an error (for reviews see Taylor et al. 2007; Wessel, 2012; Chavarriaga et al., 2014). However, none has done so on the trial-by-trial level. Zander and colleagues (2016) recently demonstrated in a grid based cursor control paradigm that EEG correlates of prediction errors directly corresponded to the size of the angular deviation, allowing these to be used to decode the amount of deviation from user expectation. This evoked activity also shared the characteristic morphology and timing of other error-related potentials, originating from medial prefrontal cortex and exhibiting a linear correspondence to the degree of expectation violation. Likewise, in the current gait challenge experiment, the rhythmic cueing and cue-step synchrony goal produced a strong prediction/expectation as to when the next cue should occur. The perceived size of the timing prediction error directly influenced the SDN as well as the subsequent behavioral adaptation.

4.3. Relationship to previous gait studies

A recent review of step adaptation has suggested that avoiding physical obstacles while walking, for example, involves decision making and movement reprogramming (reviewed in Potocanac et al., 2017). Such adjustments can be considered “voluntary” compared to automatic adjustments that may only involve small and unconscious corrections, as for example during ‘smooth’ continuous walking tasks. Such ‘automatic’ or ‘sub-conscious’ adjustments of reaching movements have been proposed to involve posterior parietal cortex (PPC) (Desmurget et al., 1999,2001; Pisella et al., 2000; Gréa et al., 2002), or alternatively subcortical structures including cerebellum (for review see Gaveau et al., 2014). Voluntary adjustments such as in our gait adaptation task, require conscious perception of the deviation and subsequent movement correction that involve prefrontal cortex (PFC).

In a previous study of these same gait adaptation data, we have shown that initial large (SOA_1,2) step adjustments also recruited PFC activity in the form of a fast transient increase of beta band power ~500ms after C₀ in the EEG (Wagner et al., 2016). This frontal beta power increase during step adaptation occurred around SOA_1,2 corresponding to the period of step adaptation and thus later than the SDN. Interestingly this right frontal beta power increase occurred only for step advance perturbations, whereas the SDN occurred mostly relative to step delay delay perturbations. As we have discussed in Wagner et al. (2016), the biomechanics of shortening a step possibly require more cortical inhibition than step lengthening, which consists mostly of a propulsion of forces to lengthen the swing phase (Varraine et al., 2000). Our previous results suggest (Wagner et al., 2016) that actively shortening the swing phase may correspond to the stopping of an ongoing response requiring top-down inhibitory control (Wagner et al., 2016; 2018, Swann et al., 2009, Wessel et al., 2013). As our current results suggest, a larger SDN likely has beneficial effects on the step adaptation process, and may be one explanation why in our paradigm adaptation to step delay perturbations is more easy and quick than for step advance perturbations (Wagner et al., 2016). The two neurophysiological markers (SDN and beta increase) in prefrontal cortex (PFC) in this paradigm may index different aspects of a performance monitoring and motor adaptation system involved in gait adjustments, and their relationship should be investigated in further studies.

Prior studies have also shown that when walking with isochronous cues subjects overcompensate step timing deviations (Delignières & Torre, 2009; Marmelat, et al., 2014), suggesting that error-processing may be omnipresent during cued walking. We did not find error related negativities to cues C₁ and C₂ following the tempo shift (see Figures 4a and 5a - ERPs relative to C₁ and C₂ should be visible in these plots since the data are time warped to these cues). In a previous analysis of the same data, we also did not find error-related negativities, following cues during the preferred walking sequence (Wagner et al., 2016). However, it is possible that occasional error processing occurs that may elicit error-potentials, e.g. when larger deviations from cues require readjustment of steps. The same may likely happen during treadmill walking, which also acts as an external pacemaker. A future study may look at whether and how the size of SDN-like activity depends on magnitude of step-cue deviations during synchronized/steady state walking to clarify the involvement of error-processing in walking to isochronous cues. This may also have implications for the wider literature on increased gait variability in elderly and Parkinson’s and on the use of rhythmic cueing to alleviate these changes (for reviews see Lim et al., 2005, Nombela et al., 2013, Stergiou et al., 2016, Ghai et al., 2018).

In the same auditory cueing paradigm (Wagner et al, 2016) we also found a long lasting suppression of beta rhythms (up to 10 sec after C₀) in posterior parietal cortex (PPC) whose time course matched the time course of readjustment of step offsets from cues. Adjustment of step-cue difference to pre-shift step-cue timing took much longer (about 6 to 7 steps) than tempo adjustment of SOA to COA (about 2 steps) (see Wagner et al., 2016). Interestingly a prior study has shown similar mu and beta power decreases over parietal areas lasting longer than 4 sec during gradual treadmill gait-speed changes lasting 4-8 s (Lisi & Morimoto, 2015).

As has been proposed for reaching movements, we argue that the longer lasting PPC activation shown in Wagner et al. (2016) and Lisi & Morimoto (2015) represents automatic online adaptation and matching/measuring of the distance between steps to external cues (such as auditory pacing cues or sensory cues to treadmill speed changes). Initial top-down control of gait adaptation in the present auditory cue paced walking task instead recruits a fast transient beta power increase (lasting ~500 ms) in prefrontal cortex, as well as the SDN.

4.4. Conclusions

Here we show that trial-by-trial variability in SDN magnitude is not merely ‘noise’ as sometimes assumed in ERP research. Our results instead suggest that there is rich information contained in EEG trial-to-trial activity variations, and this information can be used to gain insight into how the brain supports complex movements. We show that the trial-by-trial size of the SDN in our paradigm directly predicts adaptation step size, with larger SDN deflections predicting more rapid adaptation performance. We also show that SDN magnitude in single trials was partly predicted by the size of the evoking timing error (ΔC₀). Both these results are in line with the theory of predictive coding and demonstrate that performance monitoring processes are involved in maintaining gait in the face of physical gait challenges.

4.5.1. Future directions

The ability to measure the dynamics of performance monitoring signals during complex movements can significantly facilitate addressing its relationship to motor control adjustments and the impairment of these adjustments in motor disorders and in cognitive decline (Ridderinkhof et al., 2004). There is a need for indicators and predictors for the risk of falls in the elderly and in populations with motor disorders such as Parkinson’s and stroke, since falls have been identified as one of the main causes for injury, disability and death in these populations. Research indicates that a decline in executive function is related to falls in the elderly (Mirelmann et al., 2012; Beauchet, 2009; Bloem et al., 2001; Sheridan et al., 2003; Woollacott & Shumway-Cook, 2002), and to the severity of gait disorders in Parkinson’s patients (Yogev, 2005; Hausdorff, 2006, 2013).

However, the executive functions involved, and their neurophysiological substrates, have not been much investigated in humans. A recent behavioral gait study suggests that elderly persons have a decreased ability to implement top-down inhibitory control during obstacle stepping (Potocanac et al., 2015), and a recent mobile EEG study showed that elderly persons may have less flexible resource allocation during walking when performing a secondary cognitive task (Malcolm et al., 2015). Our results show the direct involvement of the performance monitoring system in gait adaptation and suggest that the SDN may be a good candidate to investigate as a biomarker for falls in the elderly and in Parkinson’s.

The possible relationship between SDN and dopaminergic (DA) transmission is especially of interest as Parkinson’s patients are known to have dopamine depletion in the brain motor system. Pharmacological studies in healthy volunteers have shown that systemic administration of DA agonists enlarges and DA antagonists reduces the ERN (Jocham et al., 2009; Barnes et al., 2014). Intriguingly, in Parkinson’s disease, when DA is depleted (mostly from the striatum), ERN amplitude is reduced and becomes unresponsive to changes in medication (Stemmer et al, 2007; Willemsen et al., 2008). This could indicate a deficiency in the performance monitoring system in Parkinson’s, with consequential inability to accurately match environmental stimuli to internal predictions and thus adapt gait to external challenges, leading to increased numbers of falls.

Our results suggest that performance monitoring processes are directly involved in appropriate adaptation of gait to changing external requirements and challenges and are indexed by cortical field dynamics that can be measured by source-resolved analysis of scalp EEG data. The results we report here suggest the possibility of investigating age- and disease-associated impairments of these control processes in gait disorders with a goal of developing biomarkers for use in fall risk prediction in conditions including early-stage Parkinson’s.

Highlights.

Participants walked on a treadmill in synchrony with a pacing cue train.

Occasional ‘late’ cue tones announced a shift to a slower pacing tempo.

These ‘late’ cues evoked a negative-going ERP peaking 250 ms after cue onset.

This peak indexed both the need for and magnitude of subsequent gait adjustment.

Adapting gait to external challenges involves cortical performance monitoring.