Fig. 1.

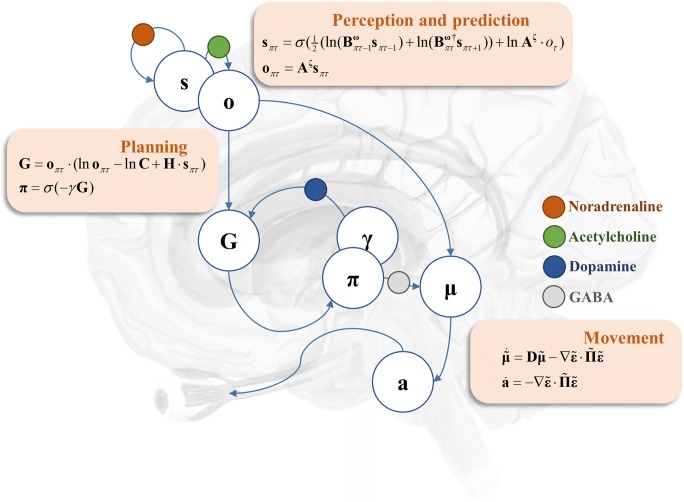
Computational neuropharmacology and oculomotion. This schematic illustrates a simplified (computational) anatomy of oculomotor control, highlighting some of the key synapses at which neuromodulatory transmitters act. The cortical components of this network include the frontal eye fields and the dorsolateral prefrontal cortex. We have associated these regions with beliefs about hidden states (s), and predictions about the (categorical) outcomes (o) that these states entail. The ‘perception and prediction’ panel specifies how these are computed from beliefs about the way in which states give rise to observations (A), and beliefs about how states at a given time evolve (B). These likelihood and prior transition terms are equipped with precisions—superscripts ζ and ω, respectively—that quantify the confidence (inverse variance) of associated conditional beliefs. The likelihood and prior precisions have been associated with cholinergic and catecholaminergic modulation respectively. These cortical regions project to both the basal ganglia (i.e. the striatum) and the superior colliculus. The direct pathway through the basal ganglia itself targets the superior colliculus, via the substantia nigra pars reticulata. Striatal neurons are modulated by dopaminergic projections from the substantia nigra pars compacta (γ), while the projections from the pars reticulata to the superior colliculus provide a GABAergic modulation of the cortico-collicular pathway (Π). The ‘planning’ panel shows how the basal ganglia may evaluate alternative saccades by computing the expected free energy (G) associated with each eye movement and subsequent sensory samples. Dopamine modulates confidence in beliefs about the best saccade to select (π), given this evaluation. The ‘movement’ panel provides the (Bayesian filtering) equations that may be used to implement the next saccade. These rely upon prior beliefs about where the eyes should be that are obtained from the predictions from the cortex (o) modulated by plans evaluated in the basal ganglia (π). Together, these are used to compute the average belief about where to look next, which is then equipped with a precision (Π). The error (ε) between current beliefs about the position of the eyes (μ) and the target is then used to drive brainstem reflexes that act (a) to minimise this error—implementing the motor command from the cerebrum. The form of these equations may look complicated; however, they can be derived in a fairly straightforward way from standard (variational message passing) schemes under ideal Bayesian observer assumptions. From our perspective, the key feature of these equations is that they suggest a modulatory role for the precisions described above. For a more detailed technical account of these equations, please see (Friston et al. 2017b), and for a conceptual overview of their relationship to anatomy, please see (Parr and Friston 2018b)