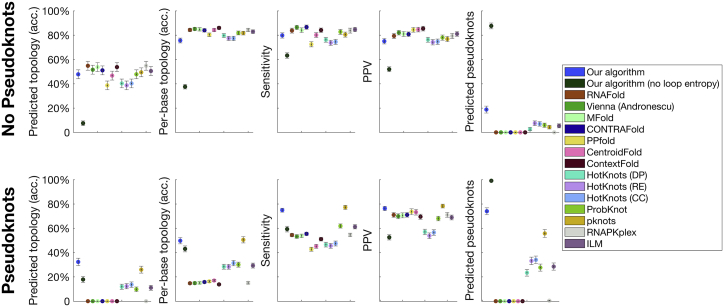
Figure 4.

Summary statistics for comparison to other prediction tools. To assess the relative success of our algorithm, we compare its performance in predicting experimentally determined RNA structures to that of 14 other current prediction tools: RNAFold (33, 118), ViennaRNA (Andronescu parameters) (119), Mfold (32), CONTRAfold (120), PPfold (121), CentroidFold (122), Context Fold (123), HotKnots (Dirks-Pierce parameters), HotKnots (Rivas-Eddy parameters), HotKnots (Cao-Chen parameters) (63), ProbKnot (40), PKNOTS (44), RNAPKplex (33, 118), and iterated loop matching (ILM) (38). We measure sensitivity, PPV, the fraction of topologies predicted correctly by the MFE structure, the average per-base topology accuracy (defined in the main text), and the fraction of MFE structures containing a pseudoknot. We separate the results into sequences that experimentally form pseudoknots and those that do not. Error bars show the standard error. Despite the fact that our algorithm requires only two parameters to describe the entropy of any arbitrary secondary structure (at least an order of magnitude–and often several–fewer than the other algorithms tested against) and that the parameters were trained on non-pseudoknotted structures, our algorithm outperforms the other algorithms tested in predicting pseudoknotted structures and performs on par with them in predicting non-pseudoknotted structures. We also demonstrate that our algorithm’s success is dependent on the accuracy of our loop entropy model because setting all loop entropies to zero (dark green) leads to poor performance (see main text for further discussion). To see this figure in color, go online.