Visual Mismatch and Predictive Coding: A Computational Single-Trial ERP Study

Abstract

Predictive coding (PC) posits that the brain uses a generative model to infer the environmental causes of its sensory data and uses precision-weighted prediction errors (pwPEs) to continuously update this model. While supported by much circumstantial evidence, experimental tests grounded in formal trial-by-trial predictions are rare. One partial exception is event-related potential (ERP) studies of the auditory mismatch negativity (MMN), where computational models have found signatures of pwPEs and related model-updating processes. Here, we tested this hypothesis in the visual domain, examining possible links between visual mismatch responses and pwPEs. We used a novel visual “roving standard” paradigm to elicit mismatch responses in humans (of both sexes) by unexpected changes in either color or emotional expression of faces. Using a hierarchical Bayesian model, we simulated pwPE trajectories of a Bayes-optimal observer and used these to conduct a comprehensive trial-by-trial analysis across the time × sensor space. We found significant modulation of brain activity by both color and emotion pwPEs. The scalp distribution and timing of these single-trial pwPE responses were in agreement with visual mismatch responses obtained by traditional averaging and subtraction (deviant-minus-standard) approaches. Finally, we compared the Bayesian model to a more classical change model of MMN. Model comparison revealed that trial-wise pwPEs explained the observed mismatch responses better than categorical change detection. Our results suggest that visual mismatch responses reflect trial-wise pwPEs, as postulated by PC. These findings go beyond classical ERP analyses of visual mismatch and illustrate the utility of computational analyses for studying automatic perceptual processes.

SIGNIFICANCE STATEMENT Human perception is thought to rely on a predictive model of the environment that is updated via precision-weighted prediction errors (pwPEs) when events violate expectations. This “predictive coding” view is supported by studies of the auditory mismatch negativity brain potential. However, it is less well known whether visual perception of mismatch relies on similar processes. Here we combined computational modeling and electroencephalography to test whether visual mismatch responses reflected trial-by-trial pwPEs. Applying a Bayesian model to series of face stimuli that violated expectations about color or emotional expression, we found significant modulation of brain activity by both color and emotion pwPEs. A categorical change detection model performed less convincingly. Our findings support the predictive coding interpretation of visual mismatch responses.

Introduction

According to predictive coding (PC), sensory systems operate under hierarchical Bayesian principles to infer the causes of their sensory inputs. This rests on message passing among hierarchically related neuronal populations: each level sends predictions to the level below and receives precision-weighted prediction errors (pwPEs), which serve to update predictions, in return (Rao and Ballard, 1999; Friston, 2005; Hohwy, 2013; Clark, 2015). This process of perceptual inference is optimized by learning, where pwPEs to repeated sensory events are explained away with increasing efficiency, mediated by plastic changes in synaptic connections of the sensory circuits (Friston, 2005; Baldeweg, 2006).

Perceptual learning experiments often use stimulus repetition to establish expectations. An experimental protocol frequently used to study implicit perceptual learning in audition is the “roving standard” paradigm (Haenschel et al., 2005; Garrido et al., 2008; Costa-Faidella et al., 2011a,b; Moran et al., 2013; Schmidt et al., 2013; Auksztulewicz and Friston, 2015; Komatsu et al., 2015; Takaura and Fujii, 2016). This repeats a stimulus several times before unpredictably switching to a different stimulus train. This paradigm is frequently used to elicit the “mismatch negativity” (MMN), an event-related potential (ERP) that signals violations of statistical regularities during perceptual learning. Although the MMN was primarily investigated in the auditory modality (for review, see Näätänen et al., 2010, 2012), there is increasing evidence for MMN also in the visual modality (for review, see Stefanics et al., 2014; Kremláček et al., 2016).

Since its discovery, the MMN response has been interpreted in different ways. First, the “memory-trace” or “change-detection” hypothesis (Näätänen et al., 1989, 1993; Schröger, 1998) conceptualized the MMN as a brain response signaling the difference between the immediate history of the stimulus sequence and a novel stimulus. Later, this interpretation was followed by the “regularity violation” hypothesis (Winkler, 2007), according to which the MMN signals a difference between the current stimulus and expectations based on prior information that might not only represent a sensory memory trace but also more complex or abstract rules extracted from regular relationships between preceding stimuli (e.g., conditional probabilities; Paavilainen et al., 2007; Stefanics et al., 2009, 2011; for review, see Paavilainen, 2013). This interpretation is compatible with the most recent view of the MMN as an expression of pwPEs during PC (Friston, 2005; Baldeweg, 2006; Stephan et al., 2006; Wacongne et al., 2011; Lieder et al., 2013a; Stefanics et al., 2015). In fact, a PC view of MMN can be seen as mathematically formalizing ideas already inherent to the earlier “regularity violation” hypothesis.

The PC interpretation of MMN is supported by much, albeit mostly indirect, experimental evidence (Garrido et al., 2007, 2013, 2017; Stefanics and Czigler, 2012; Phillips et al., 2015; Auksztulewicz and Friston, 2016; Chennu et al., 2016). By contrast, experimental studies based on formal trial-by-trial computational quantities are rare, almost entirely restricted to the auditory domain, and typically focused on specific sensors or time windows (Lieder et al., 2013b; Kolossa et al., 2015; Jepma et al., 2016). Here, we go beyond previous investigations and use a Bayesian model [the Hierarchical Gaussian Filter (HGF)] to examine whether visual mismatch responses reflect pwPEs, a hallmark of PC.

Specifically, our paradigm used a roving design in which two features of human faces were altered probabilistically and orthogonally: color and emotional expression. We used the HGF to generate pwPE trajectories and tested the implication by PC, that trial-by-trial brain activity would reflect these computational quantities. In addition, we applied a trial-wise change detection (CD) model (Lieder et al., 2013b) and evaluated the explanatory power of both hypotheses by statistical model comparison. Finally, we analyzed visual mismatch responses [i.e., visual MMN (vMMN) responses; for review, see Stefanics et al., 2014; Kremláček et al., 2016] obtained with traditional averaging and subtraction methods, and compared the results to those obtained by modeling.

Materials and Methods

Ethics statement.

The experimental protocol was approved by the Cantonal Ethics Commission of Zurich (KEK 2011-0239/3). Written informed consent was obtained from all participants after the procedures and risks were explained. The experiments were conducted in compliance with the Declaration of Helsinki.

Subjects.

Thirty-nine neurologically normal subjects volunteered in this experiment. One subject's data were excluded due to excessive blinks, and four subjects' data were rejected because of bridges between electrodes due to conductive gel. The final sample comprised 34 subjects (mean age, 23.88 years; SD, 3.56 years; 17 females; 33 right handed). All subjects had normal or corrected-to-normal vision.

Paradigm.

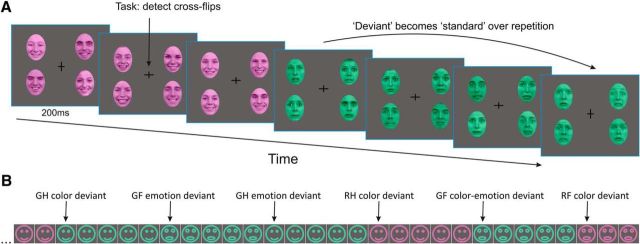
We used a multifeature visual roving standard paradigm to elicit mismatch responses (prediction errors) by rare changes in color (red, green), emotional expression (happy, fearful) of human faces, or both. Roving paradigms have often been used to elicit automatic sensory expectations in the auditory modality by manipulating stimulus probabilities (Haenschel et al., 2005; Garrido et al., 2008; Moran et al., 2013; Auksztulewicz and Friston, 2015). Here, we presented four types of visual stimuli (green fearful, green happy, red fearful, and red happy faces). Hence, each stimulus type could violate expectations either about the color or the emotional expression of faces (or both). Importantly, this allowed us to study brain responses to stimuli that were physically identical but differed in whether color or emotion regularities were violated. Faces were presented in four peripheral quadrants of the screen (Fig. 1A). Each stimulus type was presented with an equal overall probability (p = 0.25) during the experiment. After five to nine presentations, each stimulus type was followed by any of the other three types with equal overall transition probabilities (Fig. 1B). Participants engaged in a central detection task that required speeded button-presses to changes of the fixation cross. Reaction times were recorded. The experiment consisted of 14 blocks, each lasting ∼8 min. A short training session preceded the EEG recording.

Figure 1.

Stimuli and paradigm. A, We used a multifeature visual roving standard paradigm to elicit PEs by rare changes of either color (red, green) or emotional expression (happy, fearful) of human faces (or both). This allowed us to study brain responses to stimuli that were physically identical but differed in whether color or emotion regularities were violated. Faces were presented in four peripheral quadrants of the screen. A detection task was presented at fixation at the center. Faces were reproduced with permission of the Radboud Faces Database (www.rafd.nl). B, Schematic illustration of a stimulus sequence showing transitions between stimulus types. Note physically identical stimuli taking the role of different deviant stimulus types (GH, green happy; GF, green fearful; RH, red happy; RF, red fearful faces) depending on expectations established by prior stimulus context.

Face stimuli, 10 female and 10 male Caucasian models, were selected from the Radboud Faces Database (Langner et al., 2010; www.rafd.nl) based on their high percentage of agreement on emotion categorization (98% for happy, 92% for fearful faces). To control low-level image properties, we used the SHINE toolbox (Willenbockel et al., 2010) to equate luminance and spatial frequency content of grayscale images of the selected happy and fearful faces. The resulting images were used to create the colored stimuli.

Faces were presented on a CRT monitor on a dark-gray background at a viewing distance of 1 m. The width and height of each face subtended 3.8° and 5.4° visual angles, respectively. The horizontal and vertical distance of the center of the face stimuli from the center of the screen was 3.15°. To avoid potential local adaptation effects, each stimulus panel consisted of four faces with different identities (two females, two males), and the presentation order of the faces with different identity was randomized with the restriction that a face with the same identity was not presented in adjacent trials. Each face was presented with the same probability over the experiment. Stimuli were presented for 200 ms, followed by a random interstimulus interval of 600–700 ms, during which only the fixation cross was present. Stimuli were presented using Cogent2000 (http://www.vislab.ucl.ac.uk/Cogent/index.html).

EEG recording and preprocessing.

During the experiment, participants sat in a comfortable chair in an electromagnetically shielded, sound-attenuated, dimly lit room. Continuous EEG was recorded from 0.016 Hz with a low-pass filter at 100 Hz using a QuickAmp Amplifier (Brain Products). The high-density 128-channel electrode caps had an equidistant hexagonal layout and covered the whole head. EEG was referenced against the common average potential; the ground electrode was placed on the right cheek. Electrodes above the eyes and near the left and right external canthi were used to monitor eye movements. Data were digitized at 24-bit resolution and a sampling rate of 500 Hz and filtered off-line between 0.5 and 30 Hz using zero-phase shift, infinite-impulse response Butterworth filter. Built-in and self-developed functions as well as the freeware SPM12 toolbox (v6470; RRID:SCR_007037; Litvak et al., 2011) in the Matlab development environment (MathWorks) were used for subsequent off-line data analyses. Electrode positions and fiducials were digitized for each subject using an infrared light-based measurement system and Xensor software (ANT).

Epochs extending −100 ms before to 500 ms after stimulus onset were extracted from the continuous EEG. Epochs were baseline corrected using the 100 ms prestimulus period. A topography-based artifact correction method (Berg and Scherg, 1994) implemented in SPM12 was used to correct for eye-blink and eye-movement artifacts. Electrode positions were used to coregister EEG data to a canonical MRI template to calculate a forward model to define topographies of blink and eye-movement artifacts that were removed from the epoched data. To avoid other potential artifacts, epochs with values exceeding ±100 μV on any EEG channel were rejected from the analysis.

Modeling belief trajectories.

We used the HGF (Mathys et al., 2011; Mathys et al., 2014) to simulate computational trajectories to create parametric regressors for the general linear model (GLM) analysis. The HGF is a generative (Bayesian) model of perceptual inference and learning that represents a variant of PC in the temporal domain and has been used in several recent studies to investigate hierarchical PE responses in the brain (Iglesias et al., 2013; Hauser et al., 2014; Schwartenbeck et al., 2015; Vossel et al., 2015; Lawson et al., 2017; Powers et al., 2017). It is implemented in the freely available open source software TAPAS (http://www.translationalneuromodeling.org/tapas). The HGF consists of a perceptual and a response model, representing a Bayesian observer who receives a sequence of inputs (stimuli) and generates behavioral responses. The perceptual model describes a hierarchical belief updating process (i.e., inference about hierarchically related environmental states that give rise to sensory inputs). In our MMN paradigm, the ERP-eliciting face stimuli did not require a behavioral response. Therefore, we used only the perceptual model to simulate belief trajectories about external states (e.g., the occurrence of a red vs green, or a fearful vs happy face) without specifying a decision model.

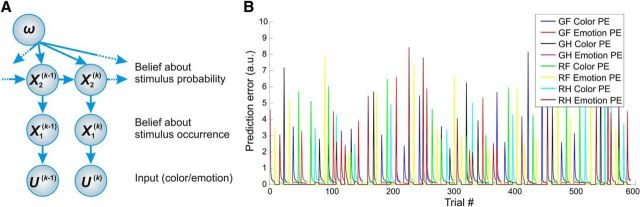
The HGF (Fig. 2A) describes how hidden states (x) of the world generate sensory inputs (u). Model inversion infers these hidden states from sensory inputs; this is equivalent to updating the beliefs across the HGF hierarchy. Here, we used a two-level version of the HGF (based on toolbox v2.2) where we eliminated the third level from the most commonly used hierarchy. This model assumes a stable volatility over the time course of the experiment, which is in line with the stimulus sequence. The first level of the model represents a sequence of beliefs about stimulus occurrence x₁. This corresponds to beliefs about environmental states (i.e., whether a green vs red face or a happy vs fearful face was presented). The second level represents the current belief of the probability that a given stimulus occurs (i.e., the tendency x₂ toward a given feature (e.g., the conditional probability of seeing a red face vs a green face, given the previous stimulus).

Figure 2.

The HGF and pwPE trajectories. A, A graphical model of the HGF with two levels (figure modified from Mathys et al. [2011] with permission under the Creative Commons licence). B, Model-based pwPE trajectories from one experimental block used as regressors in the GLM. GF, green fearful; GH, green happy; RF, red fearful; RH, red happy faces; a.u., arbitrary units.

The model assumes that environmental hidden states evolve as a Gaussian random walk, such that their variance depends on the state at the next higher level (Mathys et al., 2011, 2014), as follows:

where k is a trial index and s is a sigmoid function, as follows:

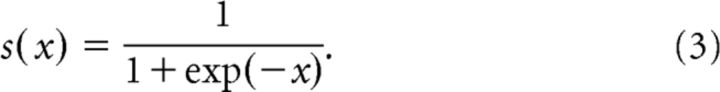At the second level, the top level in our implementation (Eq. 2), the step size between consecutive time steps depends on ω.

Exact Bayesian inversion requires analytically intractable integrations, therefore the HGF relies on a quadratic approximation to the variational energies. The variational inversion of the model provides a set of analytical update equations, which update trial-by-trial the model's estimates of the state variables. Importantly, every belief within the model is updated after each trial, leading to trial-by-trial trajectories of these hidden quantities. The update rules share a general form across the model's hierarchy: at any level i the update of the posterior mean μ_i^(k) of the state x_i that represents the belief on trial k is proportional to the precision-weighted PE ε_i^(k). This weighted PE is the product of the PE δ_i−1^(k) from the level below and a precision ratio ψ_i^(k), as follows:

The update equations of the hidden states of the HGF (level 2 here) have a general structure similar to those of classical reinforcement or associative learning models, such as the Rescorla-Wagner learning model (Rescorla and Wagner, 1972), as follows:

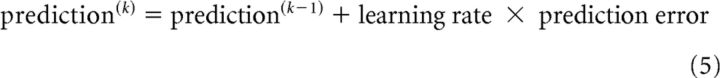We focus our EEG analysis on the pwPE on the second level ε₂, which drives learning about the probability of the stimulus. Here, we provide a brief description of the nature of this quantity. For a detailed and more general derivation of mathematical details, see Mathys et al. (2011). The update equation of the mean of the second level is as follows:

where the last term is the PE (μ₁^(k) − s(μ₂^(k−1))) at the first level weighted by the precision term σ₂^(k). This pwPE updates beliefs at the second level. The precision weight is also updated with every trial and can be regarded as equivalent to a dynamic learning rate in reward learning models (Preuschoff and Bossaerts, 2007). Thus, ε₂^(k) is not simply a scaled version of δ₁^(k).

We computed trajectories of pwPEs (with separate models for color and emotion stimuli) assuming a Bayes-optimal observer. For this, we modeled belief trajectories by estimating the parameters that would lead to minimal surprise about the stimuli. We determined these Bayes-optimal perceptual parameters by inverting the perceptual model based on the stimulus sequence alone and under a predefined prior (the standard in the HGF toolbox). Thus, our modeled observer was the same for all participants and was optimal under its prior beliefs encoded by the parameters that controlled the evolution of the estimated hidden states (Mathys et al., 2011). These trajectories capture the evolution of pwPEs—a hallmark of predictive coding—over each and every trial, peaking when a stimulus represented a change relative to previous stimuli, and subsiding over following repetitions (Fig. 2B). These model-derived trajectories can thus be used as quantitative regressors in a GLM single-trial analysis of EEG data, without the need to manually label trials as “deviants” or “surprising.” We used the absolute value of pwPE traces for the four stimulus types (Fig. 2B) to create regressors that entered the GLM, which we estimated for each participant.

Space × time statistical parametric map analysis and model comparison.

Single-trial sensor data were downsampled to 250 Hz and converted to scalp × time images for statistical analysis. Data were interpolated to create a 32 × 32 pixel scalp map for each time point in the poststimulus 50–500 ms interval. The time dimension consisted of 113 samples (of 4 ms) in each trial. Images were stacked to create a 3D space–time image volume, which was smoothed with a Gaussian kernel (full-width at half-maximum = [16 mm 16 mm 16 ms]) in accordance with the assumptions of Random Field Theory (Worsley et al., 1996; Kiebel and Friston, 2004).

We performed statistical parametric mapping across the time × sensor space, using two separate GLMs incorporating regressors from the HGF and from a more classical CD model (Lieder et al., 2013b), respectively. Both models make trial-by-trial predictions about mismatch responses, but differ in the exact form of the ensuing trajectories (HGF, gradually changing pwPEs; CD, categorical changes). For the HGF-based GLM, we included the four stimulus types as main regressors, and color-pwPEs and emotion-pwPEs as parametric modulators for each stimulus type. For the GLM based on the CD model, we included the four stimulus types as main regressors, and stick functions as parametric modulators for each stimulus type on those trials when a change occurred in the stimulus sequence. The GLMs were estimated for each participant individually.

Group-level analyses used F tests to find scalp time points where single-trial ERPs were significantly modulated by pwPEs. The resulting statistical parametric maps (SPMs) were familywise error (FWE) corrected for multiple comparisons at the cluster level (p < 0.05; with a cluster defining threshold of p < 0.001, as recommended by Flandin and Friston, 2018) using Random Field Theory. Similar preprocessing and statistical procedures have been applied previously (Henson et al., 2008; Garrido et al., 2013; Auksztulewicz and Friston, 2015).

To compare the two models formally, we used the Bayesian information criterion (BIC; Schwarz, 1978) approximation to the log model evidence (LME), separately for each participant. Under Gaussian noise (as assumed by the GLM), this leads to an approximation that is a function of the residual sum of squares (RSS), as follows:

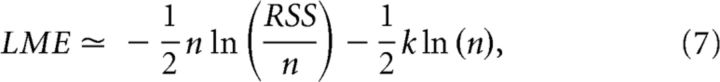where n is the number of data points and k is the number of parameters estimated by the model. Notably, in our case, n and k are the same in both models. Hence, the difference between the LMEs, and therefore model comparison, depends only on the logarithm of the RSS (i.e., model fit).

To perform model comparison at the group level, we computed the logarithm of the group Bayes factor (Stephan et al., 2007) for each voxel [i.e., the sum of ΔLME (between models) across subjects]. This corresponds to a fixed-effects group-level Bayesian model selection (Stephan et al., 2009) procedure and was done both within a functionally defined mask (of voxels showing mismatch responses under both models) as well as on all voxels in the 3D space–time image volume (to perform an unrestricted comparison). The mask comprised all voxels from the SPM analyses where, either for color or emotion changes, both the pwPE and the CD model (“logical AND” conjunction) had yielded a significant whole-brain-corrected effect. We then used a nonparametric Wilcoxon signed rank test to assess the null hypothesis of zero median for ΔLME across all voxels.

Traditional ERP analysis.

In addition to the model-based approach, we studied mismatch effects using traditional analysis methods by comparing ERP responses to deviants and standards. Deviants were defined as the first stimulus representing a change either in color or in emotion in the stimulus sequence relative to the preceding stimulus; standards were defined as responses to the same stimulus after five repetitions (the sixth presentation of the same stimulus in a row; Garrido et al., 2008). Thus, we compared responses to physically identical stimuli.

Deviant and standard ERP amplitudes were tested for significant MMN response at three posterior regions of interest (ROIs) at the left occipitotemporal, middle occipital, and right occipitotemporal regions. Regions and time windows for analysis were selected based on prior literature for color (Czigler et al., 2002; Kimura et al., 2006; Thierry et al., 2009; Czigler and Sulykos, 2010; Müller et al., 2010; Mo et al., 2011; Stefanics et al., 2011) and emotion (Zhao and Li, 2006; Astikainen and Hietanen, 2009; Kimura et al., 2012; Stefanics et al., 2012; Astikainen et al., 2013; Csukly et al., 2013; Kreegipuu et al., 2013) changes. Prior studies measured ERP amplitudes consistently at posterior occipital, temporal, and parietal regions. However, the time windows selected for analysis varied remarkably across studies in the 100–500 ms range; therefore, we adopted a flexible approach and measured ERP amplitudes to deviants and standards in 12 32-ms-long consecutive intervals in the 100–484 ms range. The effect of stimulus type on evoked responses was tested by a three-way ANOVA of stimulus type (deviant vs standard) × ROI (left vs middle vs right) × interval (12 intervals). Greenhouse–Geisser correction of the degrees of freedom was applied where appropriate; ε values are provided in the results. Significant main effects and interactions were further specified by Tukey's HSD post hoc tests.

Results

Trial-by-trial pwPE results (Bayesian model)

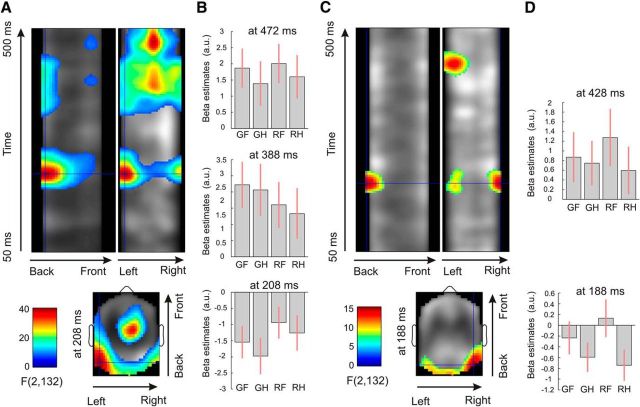
Our analysis across the time × sensor space demonstrated strong correlations among model-based pwPE trajectories, ε₂, and the single-trial ERPs (Fig. 3A), both for color and emotion. Details of test statistics are given in Table 1. F tests revealed significant activations for color pwPEs in several space × time clusters (scalp areas and time intervals). The earliest significant interval was found between 180 and 255 ms at left and right posterior regions (Fig. 3B), corresponding to a negative potential (see Fig. 5B), as well as a frontocentral positivity in a corresponding time window. We observed further correlations at a middle occipital area in the 320–430 ms interval corresponding to a positive potential, as well as negativity in a similar time window with frontocentral dominance. Furthermore, we found a middle occipitoparietal interval in the 430–500 ms time window corresponding to a positive potential, with corresponding frontocentral negativity in a similar time window.

Figure 3.

Thresholded space–time SPMs. A, Main effects of color pwPE estimates (pooled across emotions) of the F test (whole scalp corrected at p < 0.05, with a cluster-defining threshold of p < 0.001). The crosshair is positioned at the earliest maximum of test statistics. B, Contrast estimates (arbitrary units) for the four types of stimuli (GF, green fearful; GH, green happy; RF, red fearful; RH, red happy faces) at three time points of maxima in posterior clusters. Bars indicate 90% CI as additional illustration for ERP effects found after whole-scalp × epoch length FWE correction. C, D, Main effects of emotion pwPE estimates (pooled across colors) plotted similarly as for color pwPEs.

Table 1.

Test statistics for color and emotion prediction errors

Activation size (voxels)	Cluster p value (FWE corrected)	Peak p value (FWE corrected)	Peak F statistic	Peak equivalent Z statistic	Peak latency (ms)
Test statistics for color prediction errors
9885	1.44E-10	2.42E-10	40.63242	7.574789	472
		2.63E-08	32.85626	6.898473	412
		4.1E-08	32.14478	6.830418	388
		5.32E-08	31.73202	6.790405	388
3958	4.71E-06	3.9E-10	39.81532	7.50916	208
		2.11E-06	26.03102	6.192928	216
		2.6E-06	25.71183	6.156698	216
		2.5E-05	22.35084	5.753717	212
		5.9E-05	21.09702	5.592177	216
2006	0.000426	4.78E-09	35.62346	7.152807	212
9875	1.46E-10	6.09E-05	21.05077	5.586089	468
		6.31E-05	20.99963	5.579346	384
		0.000245	19.04328	5.312191	352
		0.000889	17.21467	5.044499	384
		0.002482	15.77195	4.819075	476
		0.002808	15.59909	4.791132	428
		0.003092	15.46402	4.76915	428
		0.004554	14.92295	4.679763	436
		0.010871	13.70968	4.471042	416
Test statistics for emotion prediction errors
1333	0.001824	0.00334	15.51657	4.777717	428
		0.171057	9.932535	3.729684	388
1179	0.003041	0.004358	15.14413	4.716563	188
		0.057261	11.53527	4.063691	184
		0.090418	10.87907	3.930862	180

Significant activations are arranged according to size. p Values and statistics are given for activation clusters and within each activation. Significant FWE-corrected p values are shown in italics.

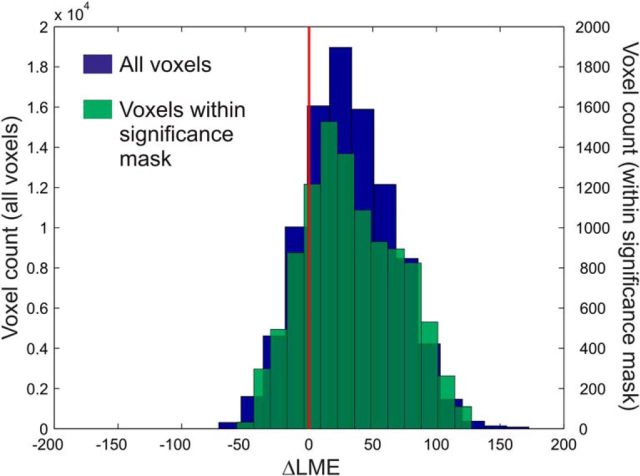
Figure 5.

Histograms of ΔLME over the voxels within a mask defined by the conjunction of significant voxels for the pwPE and change detection models either for color or emotion changes, and over all voxels in the whole 3D space–time volume.

For emotion pwPEs, F tests revealed significant activations in two space × time clusters (Fig. 3C). The earliest effects for emotion PEs were observed at a right occipitotemporal area in the 170–214 ms interval, followed by positivity at the left occipitotemporal scalp region in the 405–455 ms interval (Fig. 3D).

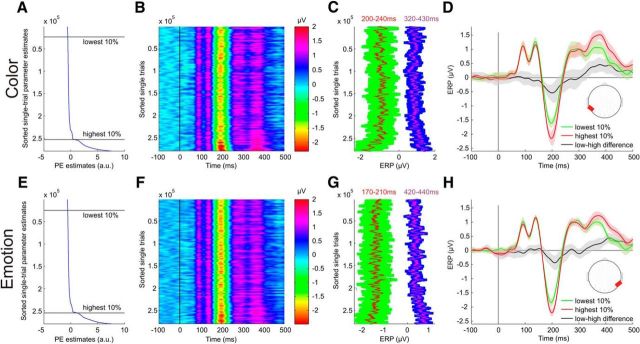
To demonstrate the relationship between the model-based pwPE parameter estimates for color changes and the MMN obtained from ERP data using traditional averaging and subtraction methods, we plotted all raw single trials sorted in an increasing order according to the trial-wise parameter estimates (Fig. 4A,B). The relationship between the computational quantities of pwPE estimates and raw data is apparent in plots showing the trial-wise ERP amplitudes (Fig. 4C) in the time windows where statistical parametric mapping yielded significant results. Calculating the mean ERP for the 10% of trials with the lowest and highest pwPE estimates, respectively, reveals characteristic ERP waveforms (Fig. 4D) that clearly differ in time intervals where classical deviant-minus-standard differences (early MMN and late positivity) have been reported previously. A similar, although less robust relationship between model-based pwPE parameter estimates for emotion changes and the ERP data is shown in Figure 4E–H.

Figure 4.

pwPE parameter estimates and ERP image of all single trials of 34 subjects (>283,000 single trials). Data in all subplots were smoothed with a sliding window of 3000 trials for visualization. A, Mean-centered parameter estimates of pwPEs to color input sorted from minimum (top) to maximum (bottom) values, yielded by the HGF. Data were smoothed using a vertical window of 3000 trials. B, Single-trial ERPs from occipitotemporal electrodes sorted according to their associated pwPE magnitude. Note vertical lines corresponding to ERP peaks and troughs. C, Mean ERP amplitudes over the intervals with significant correlation between pwPE and ERP. Red and purple lines show potential values averaged over the intervals 200–240 and 320–430 ms, respectively. Confidence intervals (SD) resulted from the time windows used per time point. D, ERP waveforms calculated across 10% of trials with the lowest and highest pwPE parameter estimates. Confidence intervals (SD) resulted from the single trials. Note the difference between waveforms in the intervals where significant pwPE-related activity has been found with multiple regression. Red areas in head plots show scalp regions where electrodes were used for plotting the ERP waveforms. E–H, Data for emotion pwPEs plotted similarly as for color above.

Comparison to the CD model

To assess whether the pwPE traces provided any advantage in modeling the EEG data compared with a classical CD model, we performed statistical model comparison. This was based on computing voxelwise log group Bayes factors [using a BIC approximation to the group-level LME difference (ΔLME)], as described in the Materials and Methods section. Figure 5 shows that the large majority of the voxels within a functionally defined mask showed strong evidence for the pwPE model (median ΔLME = 29.14; mean ΔLME = 33.48; SD = 37). ΔLME values within the whole 3D space–time volume showed very similar results (median ΔLME = 29.31; mean ΔLME = 31.34; SD = 34.86). Notably, a difference in LME of >5 is considered as very strong evidence in favor of the superior model (Kass and Raftery, 1995).

To characterize the distribution of ΔLME values more formally, we performed null hypothesis testing. An initial one-sample Kolmogorov–Smirnov test indicated that the distributions of ΔLME for voxels within our functionally defined mask (D = 0.78, p < 10⁻⁵) as well as for the whole 3D space–time volume (D = 0.79, p < 10⁻⁵) were not Gaussian. A nonparametric Wilcoxon signed rank test was used to test the null hypothesis of zero median for the ΔLME. The results showed that the median ΔLME was significantly different from zero (Z = −70.63, p < 10⁻⁵) for voxels within the mask, as well as for voxels within the whole volume (Z = −213.10, p < 10⁻⁵). Distributions of ΔLME values within the significance mask and the entire 3D space–time volume are shown in Figure 5. These results indicate the superiority of the Bayesian model over the CD model and suggest that visual mismatch responses are better explained by pwPEs than by categorical change indices.

Traditional ERP results

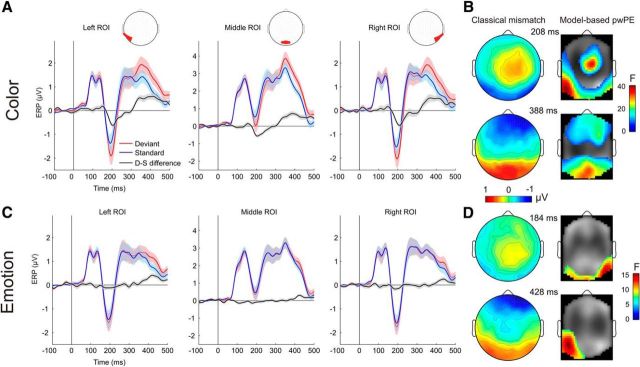
Figure 6, A and B, shows grand average ERPs to color-deviant and standard as well as to emotion deviant and standard stimuli, respectively, at occipitotemporal/occipital ROIs. Stimuli evoked the canonical P1, N1/N170, and P2 components. Deviant-minus-standard difference waves show a typical visual mismatch negativity at ∼200 ms for color changes, followed by a positive potential after 300 ms. ERP waveforms obtained with traditional averaging and subtraction methods reveal a smaller negativity for emotion changes peaking before 200 ms in the right ROI followed by a positivity after 400 ms that is most robust on the left ROI (Fig. 6C,D).

Figure 6.

ERP waveforms, scalp voltage maps, and topographic statistical parametric maps. A, ERPs with 95% confidence interval for changes in color obtained with traditional averaging deviant-minus-standard subtraction. Red areas in channel layout plots show scalp regions where electrodes were used for plotting the ERP waveforms. B, Scalp potential plots of deviant-minus-standard difference waveform (left) at two time points of cluster maxima where SPM analysis yielded significant results. Statistical parametric maps (right) for model-based color pwPE estimates (pooled across emotions) of the F test. Note the high similarity of topographic distributions for the traditionally obtained mismatch responses (with negative and positive posterior scalp distributions) and the SPM obtained with computational model-based analyses. C, D, Data for the emotion changes, plotted similarly as for color.

The ANOVA of the amplitude values for color deviants and standards yielded a significant interaction of stimulus type × interval (F_(11,363) = 14.491, p < 0.00001, ε = 0.369, η² = 0.305). A post hoc Tukey's test revealed that the interaction was caused by more negative responses to deviant stimuli compared with standards in the 196–228 ms interval, and by more positive responses to deviant stimuli compared with standards in five time windows comprising the continuous 324–484 ms interval (all p < 0.01). Significant main effects of ROI and interval, as well as their interaction were also observed but were not analyzed further.

The ANOVA of the amplitude values for emotion deviants and standards yielded a significant interaction of stimulus type × interval (F_(11,363) = 3.169, p < 0.01, ε = 0.45, η² = 0.087). A post hoc Tukey's test revealed that the interaction was caused by more positive responses to deviant stimuli compared with standards in the 420–452 ms interval (p < 0.01). Significant main effects of ROI and interval as well as their interaction were also observed but were not analyzed further.

Reaction time and hit rate

Reaction times (RT) and hit rates for the occasional changes in the fixation cross were compared between experimental blocks. Mean RT was 593 ms (SD = 116). ANOVA of RTs across the 14 blocks yielded a significant effect (F_(13,312) = 3.78; p < 0.025, Greenhouse–Geyser adjusted; ε = 0.174), with an effect size of η² = 0.14. A post hoc Tukey's HSD test revealed that the effect was caused by the significantly longer RTs in the first block compared with the rest of the blocks (p < 0.05), indicating rapid adjustment during the first block followed by a steady performance speed throughout the experiment.

The mean hit rate was 93.28 (SD = 5.76). ANOVA of hit rate across the 14 blocks yielded a marginally significant effect (F_(13,312) = 2.32; p < 0.06, Greenhouse–Geyser adjusted; ε = 0.3), with an effect size of η² = 0.09. A post hoc Tukey's HSD test revealed that the effect was caused by the significantly lower hit rate in the first block compared with those in blocks 8, 9, 10, 12, 13, and 14 (p < 0.05), indicating a steady and high performance throughout the experiment following initial adjustment to the task during the first block.

Discussion

Beginning with the seminal article by Rao and Ballard (1999), PC has become an extremely influential concept in cognitive neuroscience and currently represents one of the most compelling computational theories of perception. An experimental paradigm that was suggested early on as a suitable probe of PC in humans is the auditory MMN (Friston, 2005; Baldeweg, 2006; Stephan et al., 2006). The MMN is attractive for studies of PC, not least because the statistical structure of the stimulus sequences can be manipulated easily. This allows for straightforward tests of general predictions from PC, for example, concerning the impact of (un)predictability on ERPs. Indeed, the results from numerous auditory MMN studies are consistent with these general predictions (Wacongne et al., 2011; Schmidt et al., 2013; Phillips et al., 2015; Chennu et al., 2016; Garrido et al., 2017).

By contrast, an opportunity that has remained surprisingly unexploited is that models of PC provide formal quantities, specifically pwPEs, and predict how these should fluctuate trial by trial, given a particular stimulus sequence. While some sophisticated computational treatments of single-trial variations in evoked auditory and somatosensory EEG responses exist (Ostwald et al., 2012; Lieder et al., 2013b; Kolossa et al., 2015), these have examined other potentials than MMN, were restricted to particular electrodes and time points, or used computational quantities different from pwPEs (e.g., Bayesian surprise). In the domain of visual mismatch, computational investigations have been lacking entirely so far.

To our knowledge, this study represents the first computational single-trial EEG analysis of the vMMN. It demonstrates that visual mismatch responses reflect trial-wise pwPEs, a core quantity of PC, and thus supports the general notion that MMN can be understood as a hierarchical Bayesian inference process (Friston, 2005; Garrido et al., 2009). Specifically, we used a Bayes-optimal agent for belief trajectories about probabilities of two features of human faces: color and emotion. pwPE estimates for both features showed a significant relationship to event-related potentials at the single-trial level (Fig. 3), with activations at electrodes and time windows that were comparable to classical vMMN results (see below). Sorting single-trial ERPs according to the magnitude of the model-based pwPE estimates and selecting those with the highest and lowest pwPEs revealed the characteristic negative mismatch waveform at posterior electrodes (Fig. 4). These findings suggest that the MMN is a correlate of pwPEs as computed by a hierarchical Bayesian model. Comparing our model-based results to those obtained with traditional averaging and subtraction methods revealed that time course and topographic distributions of the two analyses yielded highly similar results (Fig. 6).

The high hit rate and approximately constant RT over the experiment indicates that participants complied with the task and attended the fixation cross. Hence, the pwPEs observed in our study were likely generated by an automatic mechanism that operates outside the focus of attention, in line with theories of perception as unconscious inference (Hatfield, 2002; Friston, 2005; Kiefer, 2017).

Several studies used the vMMN to investigate neural responses to changes in color and facial emotions (see Materials and Methods). The topographical distribution and time course of pwPEs in our current study are in line with these previous findings. However, to our knowledge, our study is the first to demonstrate that pwPEs obtained from a formal Bayesian model (HGF) are reflected by visual mismatch responses. Thus, our results represent an important advance in the interpretation of vMMN, elucidating the potential underlying computational processes.

Our model-based approach identified an early time window of pwPE responses in the 180–255 and 170–214 ms intervals for color and emotion PEs, respectively. The topographic distribution of both responses (Fig. 6B) corresponds to the topography of the known vMMN response characterized by a posterior dominant-negative potential. These intervals are also in good agreement with our current results obtained with traditional ERP analysis methods, which showed a significantly more negative response to color deviants in the 196–228 ms interval. Traditional ERP analysis did not reveal a significant mismatch response to emotion deviants in a similarly early interval, which we discuss below.

Prior studies often observed a late positive potential following the MMN peak in the deviant-minus-standard differential response dominant at the posterior scalp (Czigler et al., 2002; Zhao and Li, 2006; Czigler and Sulykos, 2010; Müller et al., 2010; Stefanics et al., 2011). Accordingly, we found significant PEs in the 320–500 and 405–455 ms intervals for color and emotion changes, respectively, that corresponded to positive potentials at the posterior scalp (Figs. 3, 6). These intervals are in good agreement with the results obtained with traditional averaging and subtraction methods, which revealed significant mismatch responses in the 324–484 and 420–452 ms intervals for color and emotion, respectively. An important result of our current study is that the “late positive” peak also shows a significant relationship to model-based pwPE estimates. It indicates that this later potential, similar to the MMN, is also a neural correlate of PEs, despite its scalp distribution, which apparently differs from that of the MMN, which suggest that different generator sources underlie the two responses. The existence of multiple significant intervals, both for color and emotion pwPEs, are in line with PC as this posits that pwPEs are minimized in sequential steps during the model update process (Friston, 2005).

A strength of our study is that the time course and scalp topography of significant pwPE-related potentials were identified using a model-based approach that was applied to the entire time × sensor data space. This contrasts with previous studies that often restricted the statistical analysis to certain electrodes and time intervals.

We also compared our Bayesian model against a more classical alternative (change detection) to verify our computational interpretation of visual mismatch responses. This involved two GLMs incorporating either trial-wise pwPEs (from the HGF) or categorical change indices (CD model). Model comparison indicated that the pwPE model was clearly superior to the CD model in the large majority of voxels—both for a restricted mask (where both pwPE and CD models yielded significant results at the group-level) and for the entire space–time volume. Two issues are worth highlighting here. First, our Bayesian model is generic and pwPE trajectories obtained with the HGF are unlikely to differ markedly from those generated by other Bayesian models. In fact, for any probability distribution from the exponential family, Bayesian update equations share a canonical form for precision-weighted PEs (Mathys, 2016). Second, our approach is not restricted to a particular time bin (Lieder et al., 2013b) and does not preclude that competing models could explain different trial components differentially well. However, this potential problem of interpretability is addressed by our functionally defined mask, which is restricted to points in time–sensor space with significant mismatch responses under both models. Future extensions of the present approach could involve generative modeling of the entire waveform. While MMN waveform models do exist, these are detailed biophysical models that cannot be directly fitted to EEG data (Wacongne et al., 2012) and/or are not suited for single-trial analyses (Lieder et al., 2013a).

A limitation of our paradigm is that the necessity to control face stimuli for spatial frequency and luminance diminished details of facial expressions, which are important for emotion recognition. For example, an important cue for fear, the white sclera above the pupil revealed by widely opened eyes (Darwin, 1872; Ekman and Friesen, 2003), appeared remarkably diminished after equating images for spatial frequency and luminance. This might explain why our mismatch responses to emotion changes were less robust compared with previous studies (Stefanics et al., 2012) and why our current traditional ERP analysis approach did not yield a significant mismatch response in an early time window. Although our model-based analysis revealed significant emotion pwPE responses in the early time window of 170–214 ms, the effect was mainly driven by responses to happy faces (Fig. 4D). By contrast, our model-based approach did identify significant single-trial pwPE responses to emotional faces in the early time window where vMMN responses were observed in prior studies. This highlights the advantages of using a computational modeling approach in a GLM framework at the single-subject level. First, using trial-by-trial regressors in a GLM enables us to use all trials from the experiment and hence increases the robustness of the parameter estimates, whereas in traditional MMN approaches a large portion of trials are not used in the deviant versus standard comparisons. Second, our modeling approach allowed us to include trials where both color and emotion changed.

Future extensions of our current work include effective connectivity analyses, such as dynamic causal modeling (DCM) that has proven useful for our understanding of the auditory MMN (Garrido et al., 2007; Moran et al., 2013, 2014; Cooray et al., 2014; Ranlund et al., 2016). Although several electrophysiological studies are consistent with propagation of pwPEs in a hierarchical network supporting PC, the interpretation is indirect, and a direct embedding of computational quantities into physiological models remains to be done. Future studies may combine hierarchical Bayesian models with DCM to better characterize trial-wise computational message passing in neural circuitry mediating visual perception.