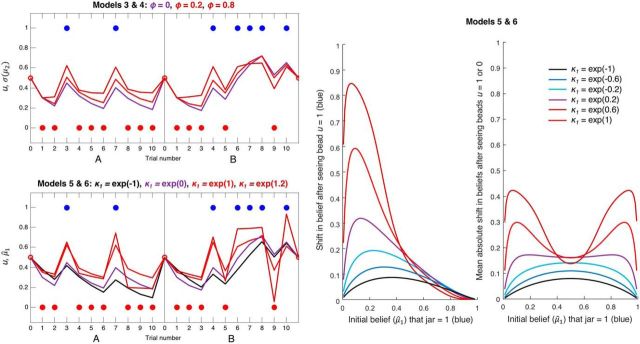
Figure 4.

Simulated data illustrating the effects of ϕ (Models 3 and 4) and κ₁ (Models 5 and 6) on inference. Both panels represent simulated perceptual model predictions in the same format as before, with σ₂⁽⁰⁾ and ω set to their previous values; hence, the purple line in these plots is identical to that in Figure 3. The second level and simulated responses y have been omitted for clarity. Top left, Simulations of a perceptual model incorporating an autoregressive order (1) process at the second level, using three different values of AR(1) parameter ϕ: 0, 0.2, and 0.8. The estimate of the tendency on trial k + 1, μ₂^(k+1), is selected from a Gaussian distribution with mean μ₂^(k) + ϕ(m − μ₂^(k)) and variance σ₂^(k) + exp(ω). Over time, μ₂ is therefore attracted toward level m (fixed to 0, i.e., at σ(μ₂) = 0.5) at a rate determined by ϕ. In effect, this gives the model a 'disconfirmatory bias,' such that as ϕ increases, σ(μ₂) is pulled further away from a belief in either jar, and toward 0.5 (maximum uncertainty about the jars). Bottom left, Simulations of a perceptual model using four different values of scaling factor κ₁, which alters the sigmoid transformation: μ̂₁^(k+1) = s(κ₁ · μ₂^(k)). When κ₁ > exp(0), updating is greater to unexpected evidence and lower to consistent evidence; when κ₁ < exp(0), the reverse is true. Red and brown lines (κ₁ > exp(0)) indicate the effects of increasingly unstable attractor networks; that is, switching between states (jars) becomes more likely (a concomitant increase in vulnerability to noise, i.e., response stochasticity, is not shown). Green line (κ₁ = exp(−1)) indicates slower updating around μ̂₁ = 0.5, as was found in controls. κ₁ permits a greater range of updating patterns than ϕ (the green and brown trajectories in the bottom cannot be produced by Model 4), which may be why Model 6 can fit both controls and Scz groups well. Middle, Plot represents the effects of κ₁ on belief updating, as a function of the initial belief μ̂₁ (σ₂⁽⁰⁾ and ω were set to 1.5 and −1, respectively, as in Fig. 5; changing these parameters does not qualitatively alter the effects of κ₁ shown here). For values of κ₁ < exp(0) = 1 (bottom three curves) and initial beliefs to the left of these curves' maxima (i.e., that the jar is probably red), relatively small increases in μ̂₁ are made if one blue bead (u = 1) is observed, such that the subject still believes the jar is most likely red. For values of κ₁ > exp(0.5) (top two curves), observing one blue bead causes such a large update for all but the most certain initial beliefs in a red jar that the subject's posterior belief is that the jar is probably blue. These subjects' beliefs are no longer stable, but neither can they reach certainty: only tiny updates toward 1 are possible for μ̂₁ > 0.8. Right, Plot represents the average absolute shifts in beliefs on observing beads of either color. This 'vulnerability to updating' is highly reminiscent of the 'energy state' of a neural network model (schematically illustrated in Fig. 1) (i.e., in low energy states); less updating is expected. The effect of increasing κ₁ is to convert confident beliefs about the jar (near 0 and 1) from low to high 'energy states' (i.e., to make them much more unstable).