TABLE I.

Summary of main predictions for the growth regime (0 < ∊ < 1) of the convex variant, with comparison to the corresponding predictions of a standard morphogenesis model. The ∊ ≪ 1 limit pertains to early development, i.e., just after the onset of shape change. The five dimensionless model parameters discussed above are written in a slightly different (but equivalent) form here in order to emphasize their physical meaning.

	Buckling without bending model	Conventional elastic bilayer model
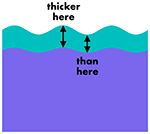
Phase relationship between film thickness and substrate deformation (the planar limit t/r → 0 is shown for simplicity)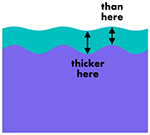
Amplitude of film thickness oscillations	= [(1 − ∊)/∊]×wrinkling amplitude	≪ wrinkling amplitude
Wave number q = (2π〈r〉)/λ	$=\sqrt{k_t/\beta \{1+(ϵc)/(1-ϵ)\}}\approx \sqrt{k_t/\beta },\text{ for }ϵ\ll 1$	~(〈r〉/t)(Ef/Es)−1/3
Near morphogenesis onset, the number of wrinkles q is independent of	Geometry	Differential strain (in excess of critical strain)
To generate more wrinkles	Increase growth potential kt or decrease gradient penalty β	Decrease film thickness (relative to system size) or decrease stiffness contrast Ef/Es
Proxy for time in developmental dynamics	∊ (see Ref. [27] for more details)	Differential strain
Minimal input physics in the form of dimensionless parameters	(i) Effective radial spring constant kr/μ(= ∊−1) presumably coming from system-spanning radial glia fibers (ii) Growth potential kt/μ of the film (iii) Thickness gradient penalty β/μ presumably coming from film-spanning fibers, e.g., Bergmann glia (iv) Preferred geometry $\sqrt{A_0}/r_0$ (v) Reference geometry t0/r0	(i) Stiffness contrast Ef/Es of two homogeneous elastic materials (ii) Zero-strain geometry ${\tau }^0/r_s^0$ (iii) Differential strain eθθ