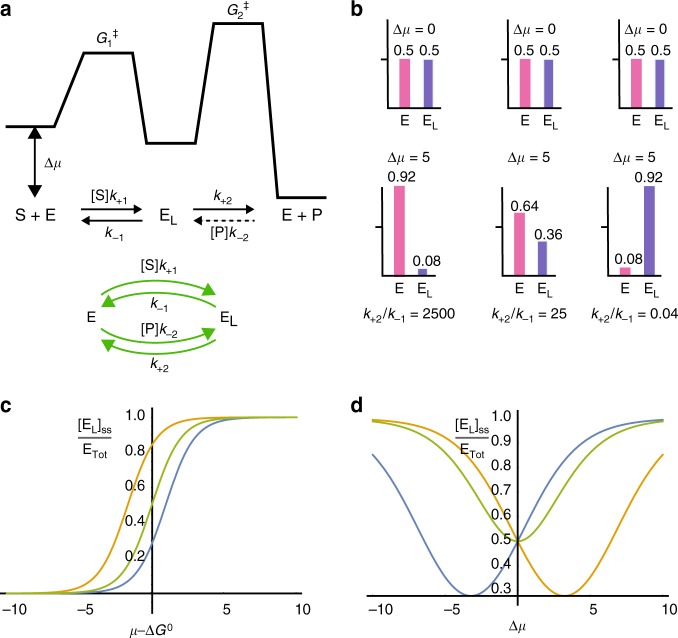
Fig. 2.

Kinetic asymmetry and Michaelis–Menten enzymes. a Energy profile for a Michaelis–Menten mechanism for catalysis, and two equivalent ways of writing the mechanism. An important quantity for determining the non-equilibrium behavior of the enzyme is the difference in transition state free-energies, $\Delta G^{‡}=G_1^{‡}-G_2^{‡}$, which can be expressed in terms of the rate constants as $\frac{k_{-1}}{k_{+2}}={\mathit{e}}^{-\Delta G^{‡}}$. This ratio does not depend on either μ or Δμ. b Bar graphs illustrating the equilibrium ($\Delta \mu =0$) distribution, where the kinetic asymmetry $k_{+2}∕k_{-1}$ has no role, and the non-equilibrium ($\Delta \mu =5$) steady-state distributions that strongly depend on the kinetic asymmetry $k_{+2}∕k_{-1}$. c, d The concentrations of substrate (S) and product (P) are taken as constant (i.e., chemo-stated) in all calculations, and can be written in terms of the chemical potential using activity coefficients $\left[\mathrm{S}\right]=a_{\mathrm{S}}{e}^{\mu +\Delta \mu }$ and $\left[\mathrm{P}\right]=a_{\mathrm{P}}{e}^{\mu -\Delta \mu }$. In ideal solutions both activity coefficients are ~ 1 in the units of concentration in which [S] and [P] are specified. Two types of enzyme adaptation: c “equilibrium” adaptation where the binding is based on the reference chemical potential $\mu -\Delta G^0,\Delta G^0=\left(G_{{\mathrm{E}}_{\mathrm{L}}}^0-G_{\mathrm{E}}^0\right)$, with $k_{-1}=5$, $k_{+2}=0.2$, and $\Delta \mu =3.4$ (orange); $\Delta \mu =0$ (green); and $\Delta \mu =-3.4$ (blue). d Non-equilibrium adaptation governed by Δμ plotted at fixed $\mu -\Delta G^0=0$. The binding is controlled by $\Delta \mu$ and by the kinetic asymmetry ($k_{+2}∕k_{-1}=25\left(\mathrm{blue}\right);k_{+2}∕k_{-1}=1\left(\mathrm{green}\right);\mathrm{and}{k}_{+2}∕k_{-1}=0.04\left(\mathrm{orange}\right)$)