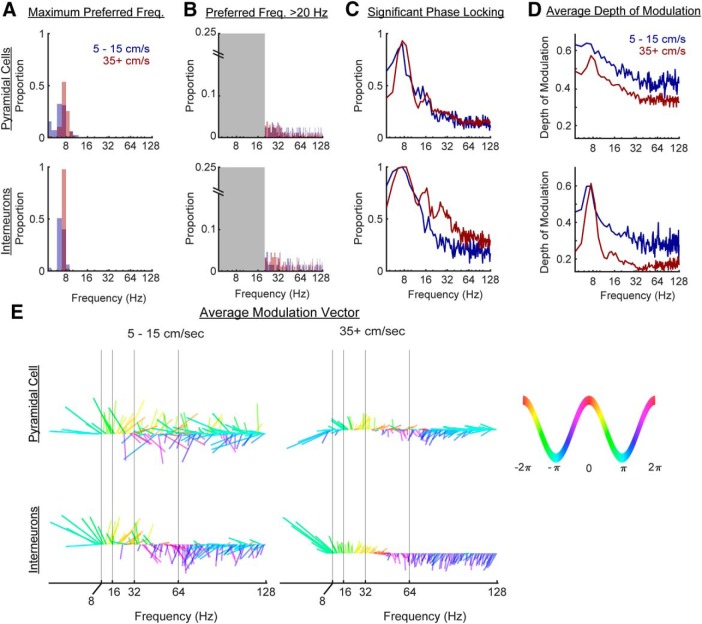
Figure 7.

Neuronal depth of modulation can be found for all frequency bands but with little evidence for a slow γ band. A, The maximum preferred phase of neuron modulation was determined for all cells should the neuron have a significant phase locking (as determined by a Rayleigh test p < 0.01). When conducting this analysis across a broad band (4–128 Hz) and as a function of velocity, it becomes evident that neurons are primarily modulated by θ. B, However, γ modulation analyses are often conducted without considering the contribution of θ. Therefore, we examined the maximum preferred phase >20 Hz. The major mass of spikes falls near the third harmonic of θ, consistent with the heavy θ modulation seen in panel A as well as hypothesized by Schomburg et al. (2014). Note the difference in y-axes between panels A, B. C, Similar to Schomburg et al. (2014), the proportion of cells that exhibited significant phase locking (as determined by a Rayleigh test p < 0.01) was plotted as a function of frequency. However, the primary difference between Schomburg et al. (2014), and the present study was that the aforementioned study implemented wavelet to determine phase, whereas the current study used a narrow band filter (see Materials and Methods). Note that the majority of cells were modulated by the 7- to 9-Hz θ rhythm. Should they exhibit a skewed distribution in their phase preference (Skaggs et al., 1996), then it is conceivable that they would also exhibit significant phase locking to harmonics. D, For each neuron that exhibited significant phase locking to a specific band, the depth of modulation was calculated. In this instance, the sparse firing of pyramidal neurons favors greater depths of modulation at lower velocities (as depth of modulation is the maximum bin value minus the minimum bin value normalized to the maximum; see Materials and Methods). At both low and high velocities, for pyramidal cells and interneurons, the maximum depth of modulation was to the θ. Although there was a large proportion of interneurons modulated by the 21- to 27-Hz harmonic of θ (C, bottom), the depth of modulation values in this range approach a minimum, hitting the lowest values in the slow γ range. E, For the significantly modulated neurons, a vector length (depth of modulation) and angle (preferred phase) was determined to allow the calculation of the average modulation vector as a function of frequency. The color and angle depict the phase (see key) while the magnitude of the line is the depth of modulation. At low velocities, there is a high degree of variance across adjacent frequencies which becomes smaller at higher velocities. For of all these plots, while it may be tempting to derive a conclusion for frequencies >16 Hz, we emphasize caution. After the θ range, spike-field coherence values fall well below 0.05 (weak coherence, despite being significant, is closer to an incoherent, random phase assignment than coherence; Fig. 8). Therefore, although it is possible to find significant coupling across the range of bands between 4 and 128 Hz, there is no rationale to suggest that a slow γ modulation exists in the spiking activity of the units.