Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2018 Oct 10;3(10):12967–12974. doi: 10.1021/acsomega.8b01643

Lamellae—Parking Garage Structure—Lamellae Transition in Densely Grafted Layers of Amphiphilic Homopolymers: Impact of Polymerization Degree

Alexei A Lazutin 1, Valentina V Vasilevskaya 1,*
PMCID: PMC6709779  PMID: 31458020

Abstract

graphic file with name ao-2018-016438_0014.jpg

By means of computer modeling, the self-organization of densely grafted macromolecules with amphiphilic monomer units as a function of macromolecular polymerization degree and solvent quality was studied and a diagram of state was constructed. The diagram contains fields of disordered distribution of monomer units and of prolonged aggregates, regions of lamellae with small and big domain spacing, and transition region. Within the transition region, the lamellae with different spacing coexist: the lamellae with big domain spacing are on the top of the grafting layer and the lamellae with small domain spacing are close to the grafting surface. The lamellae are connected with each other and form bicontinuous parking garage structure joining all side groups into a single cluster. The domain spacing of lamellae does not depend on the macromolecular length, but the width of the transition region decreases with the decrease of polymerization degree until total vanishing at relatively short macromolecules. The sharp switch between lamellae and bicontinuous structure opens the perspective for practical applications of densely grafted layers with amphiphilic monomer units.

Introduction

The brush surfaces, decorated by responsive macromolecules, could change their properties on demand of external stimuli, and thereby they are able to control adhesion and wetting, to operate as sensors, to form a coating with changeable pattern, and so forth.1−3 Responsive brush surfaces occur in nature.3−5

The self-assembly of grafted macromolecules is a complex process sensitive to many factors, among which are grafting density and solvent quality, architecture and chemical composition of macromolecules, availability of groups with different affinity to solvent and their relative content, interaction with substrate, and so forth.6−8

In a good solvent with the increase of grafting density, the macromolecules undergo a smooth transition from coil to almost a fully stretched state.9,10 The macromolecules start to stretch perpendicular to the grafting surface when the distance d between grafting points becomes comparable with macromolecular radius of gyration, Rg. It is accepted that the grafting layer is in the so-called mushroom regime when the parameter of reduced grafting density 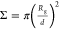Inline graphic is less than unity: Σ < 1; in brush regime at Σ > 5; and in the intermediate regime when 1 < Σ < 5.11 The macromolecular size Rg and grafting density for mushroom–brush transition depend on the solvent quality. Also, in a poor solvent, the increase of grafting density causes a sequence of transformations: single globule—compacted micelles of few polymer chains—fused micelles or stripes—reverse micelles—homogeneous layer.12−16 The homogeneous layers are literally uniform. However, different macromolecules are unequally stretched perpendicular to the substrate, and their free ends can be distributed over the whole layer.17 Such a distribution significantly increases the cumulative conformational entropy of grafted macromolecules and thus decreases the total elastic force acting on all grafted polymer chains.17−19

Diblock copolymers could repeat the above-described sequencing of morphological transformation with the growth of grafting density in case of strongly incompatible blocks and solvent being selectively poor for internal, grafted to the substrate, blocks.20−28 In other cases (relative compatibility of blocks, strong hydrophilicity or explicit hydrophobicity of external blocks, and so forth), much more complex structures are observed. There could be micelles with one or few hydrophobic cores covered by hydrophilic monomers, structured stripes, and domains oriented perpendicular to the substrate.20−28 The latter structures are formed in nonselective solvents by external blocks bent inward. Depending on their relative lengths, the external blocks can join into semispherical, cylindrical, or layered domains. These domains are deepened to the matrix of internal blocks and have no contacts with the substrate. To stress this fact, ref (28) proposes to call them “golf holes”, “stalactites”, and “ridges and gullies”, correspondingly.

Grafted layers of amphiphilic homopolymers consisting the identical and amphiphilic monomers including both hydrophobic and hydrophilic groups were addressed in refs.29−31 The presence of groups having an affinity to different solvents implies surface activity of such monomer units32,33 accounted for by the dumbbell model of monomer units.34 This model represents an amphiphilic monomer unit as two A and B beads linked with each other by covalent bonds. Some beads, for example, A, form a backbone and other beads, B, are pendants.34 It was shown that such a model allows to describe the unique conformations adopted by macromolecules with amphiphilic monomer units in dilute and concentrated solutions,34−39 to reconstruct their specific ordering in the bulk40,41 and near interface.42−44 In selective solvent, amphiphilic homopolymers sparsely grafted onto a flat substrate can form an ultrathin coating having the width of about two monomer units.29 Domains oriented perpendicularly to the substrate are observed in densely grafted amphiphilic homopolymers.30,31 Depending on the solvent selectivity, they can be strands of few macromolecules,30,31 lamellae with different periods, and parking garage structures,31 joining lamellae with different periods by screw ramps.

This article addresses the influence of macromolecular length on the structure formed in densely grafted layers of macromolecules with amphiphilic monomer units.

Simulation Model

The studied polymer brush is depicted in Figure 1. It comprises n identical macromolecules, each consisting of N amphiphilic monomer units. The amphiphilic monomer is represented as an A-graft-B dumbbell of two A and B beads linked together by a covalent bond. A beads form the polymer backbone, and B beads are side pendants. The macromolecules are tethered to the solid substrate through the fixation of A beads of the first monomer of each macromolecule in sites of square lattice with side d. The polymer brush is placed into the selective solvent being athermal for backbone A groups and poor for side B groups.

Figure 1.

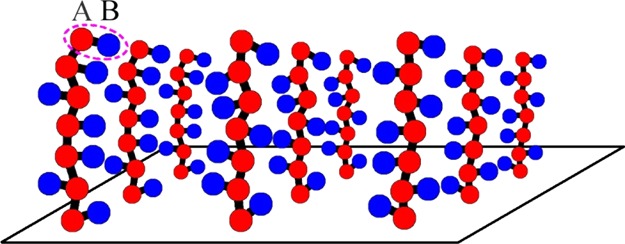
Figure 1

Open in a new tab

Schematic presentation of studied amphiphilic homopolymer brush.

The calculations are performed at a coarse-grained level using the molecular dynamic technique with the LAMMPS software package45 and resources of the Supercomputing Center of Lomonosov Moscow State University.46

The excluded volume of beads is accounted for by the shifted and truncated repulsive branch of the 12–6 Lennard-Jones (Weeks–Chandler–Andersen) potential, Ev

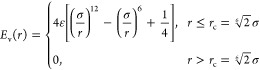graphic file with name ao-2018-016438_m002.jpg 1

where r is the distance between two particles; σ refers to the bead diameter; and ε defines the strength of the interaction in units of temperature kBT (kB is the Boltzmann’s constant). We take the diameter σ ≡ 1 as the unit of length, the energy ε ≡ 1 as the unit of energy, and subsequent results are presented in terms of these natural units.

The bonded beads interact via finitely extensible nonlinear elastic (FENE) potential, EFENE, acting between the beads adjacent along the backbone and between two beads forming A-graft-B monomer unit

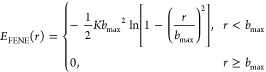graphic file with name ao-2018-016438_m003.jpg 2

where K = 30 is the spring constant, and bmax = 1.5 is the maximum bond length. An equilibrium bond length b determined by the interplay of elastic (2) and excluded volume (1) interactions with the selected K and bmax values is a little less than unity: b = 0.97.

The nonbonded monomer units interact via Yukawa-type potential, EIJ(r), accounting implicitly the solvent quality

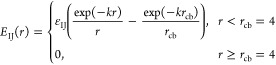graphic file with name ao-2018-016438_m004.jpg 3

where k = 1.2 is the inverse screening length, and characteristic energies εIJ are different for different groups (I, J = A, B).

In a simulation presented here, εAA = 0, εAB > 0, and εBB ≤ 0. There are no any, except excluded volume, interactions between backbone A groups, and the solvent is selectively good for them. The positive parameter εAB promotes segregation of A and B groups and ensures the surface activity of amphiphilic A-graft-B monomer units. The negative parameter εBB provides attractive interaction between side B groups and reproduces poor solvent conditions for monomer pendants: −10 < εBB < 0.

The substrate is modeled as a flat wall located at z = 0 and interacting with each bead via truncated repulsive branch of the 9–3 Lennard-Jones potential, Es(47)

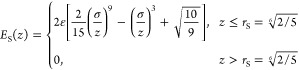graphic file with name ao-2018-016438_m005.jpg 4

where z is a distance normal to the surface.

As usual, temperature T was maintained by a Langevin thermostat with a friction term and a Langevin uncorrelated noise term Ri related to the viscosity of the solvent through the fluctuation–dissipation theorem48

graphic file with name ao-2018-016438_m006.jpg 5

where δ is the Dirac delta function; α = x, y, and z are the coordinates, i = 1, ..., nN; and parameter Γ = 0.01 in all calculations.

In each computer experiment, the polymer brush contains n = 169 macromolecules and the distance between grafting points d = 2. The degree of polymerization N changes from N = 10 to N = 100 monomer units. Thus, the reduced grafting density 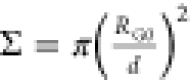Inline graphic varies from Σ ≈ 8.2 to Σ ≈ 82, where RG0 is the gyration radius of macromolecule in the melt. Our calculations show that although the backbone A–A bonds experience excessive tension, even at the highest grafting density, the average bond length was not more than 1% longer than its equilibrium value: b = 0.97.

In the initial configuration, the polymer chains were extended in the direction of the z-axis; then, the polymer brush was equilibrated for a long time with εAA = 0, εAB = 0, and εBB = 0. After that, the energy εBB was gradually increased to εBB = −10 in steps of ΔεBB = −0.25. For each value of εBB, simulations were performed during prolonged time with the integration step of 0.01τ (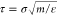Inline graphic is the unit of time) to ensure system equilibration. After that, the production stage was committed. The relaxation and production times were fitted to ensure a complete system equilibration and a rational result justification, which were checked by standard procedures.31 The full calculation time varied from 10 000τ to 60 000τ steps depending on the macromolecular length and interaction energy εBB.

The results of the calculations are discussed in the next section.

Results

Typical structures distinguished in computer experiments are shown in Figure 2. There are totally mixed state with a homogeneous distribution of A and B groups (A), prolonged aggregates (B and C), and lamellae with different domain spacing (D–F).

Figure 2.

Figure 2

Open in a new tab

Snapshots of typical structures. Top view of brush slice at height z = 15 from the surface, polymerization degree N = 50, energy εBB = 0 (a); −3.0 (b); −3.5(c); −5.5 (d); −7 (e); and −9.5 (f).

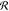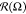As it was shown recently,31 the segregation of A and B groups is accompanied by limitation of possible directions of bond vectors r⃗AB connecting A and B groups of the monomer unit. Numerically, this effect could be accounted for by calculations of circular distribution Inline graphic of bond vectors r⃗AB(i) over orientation angle Ωi which was determined, for definiteness, as an angle between the bond projection Prxy[r⃗AB(i)] on the grafting plane XY and the axis oX: Ωi = arctan(yAB(i)/xAB(i)), where i = 1, ..., nN. 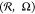The distribution Inline graphic averaged over time for different energies εBB, and polymerization degrees N are shown in Figure 3. 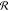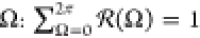The distributions are presented in polar coordinates Inline graphic with angle Ω changing in the interval 0 ≤ Ω ≤ 360° and radius Inline graphic showing the fraction of A–B bond vectors with given angle Inline graphic.

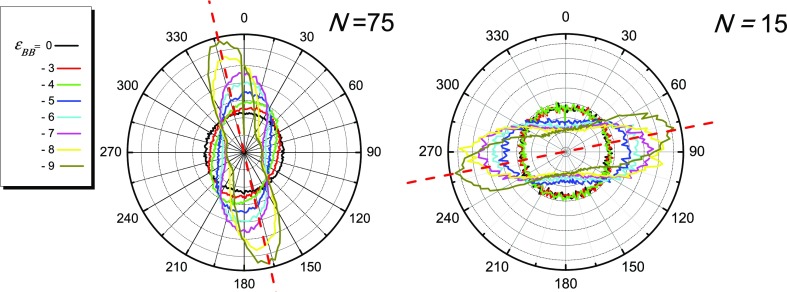
Figure 3.

Figure 3

Open in a new tab

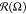Distribution Inline graphic of bond vectors r⃗AB over angle Ω for different energies εBB. N = 75 (left) and N = 15 (right). Dashed red lines indicate main directions of bond vectors at high values of |εBB|.

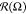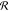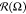It is seen that at low values of |εBB|, the distribution Inline graphic is an almost perfect circle with the center at the origin point and negligible fluctuations in radius Inline graphic. Growth of B–B attractive interaction |εBB| leads to visible deformation of Inline graphic: fraction 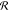Inline graphic increases for some angles Ω and simultaneously decreases for others. 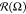In case of N = 75, at εBB > −4, the distribution Inline graphic looks similar to a flattened oval. Within interval −8 < εBB < −4, the long axis of this oval is placed parallel to oX axis. 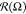Inline graphic has a maxima at Ω ≈ 0° and 180° and minima at Ω ≈ 90° and 270°. 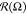The Inline graphic oval becomes thinner with the increase of |εBB|, and also at εBB = −8, it changes orientation: the long axis rotates by about 14°. 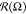Inline graphic rotation indicates the rotation of lamellae and also implies the changes of periodic structures. Lamellae of shorter macromolecules (N = 15) are arranged first parallel to oX: the bond vectors are mostly perpendicular to oX. Then, they turn by about 14° as well. We would like to mention that the size of the cell was chosen as a commensurate size of lamellae with a small domain spacing. It contains an integer number of domain spacings of such lamellae and ensures their spontaneous arrangement parallel to cell sides.49

The circular distribution 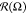Inline graphic is characterized by dispersion σΩ calculated as50

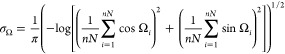graphic file with name ao-2018-016438_m023.jpg 6

The dispersion σΩ allows estimating quantitatively the range of available bond vectors r⃗AB orientations. In case of a totally free orientation of A–B bonds, the dispersion σΩ is maximal and equals unity: σΩ = 1. Any limitation on the position of A–B bonds leads to σΩ decrease.

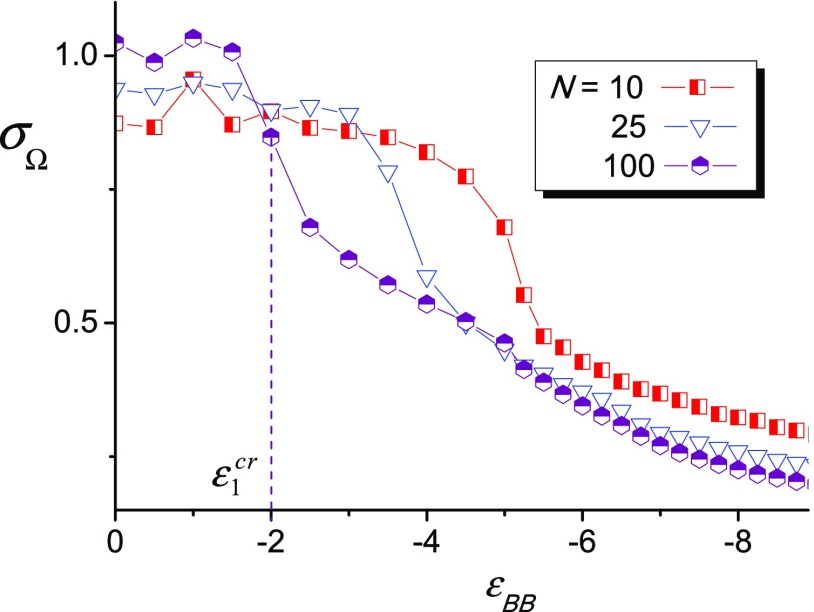
The dependences σΩ(εBB) for different N are shown in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Dispersion σΩ as a function of εBB for different polymerization degree N. Dashed vertical lines indicate critical points of transition from ordered to disordered state for N = 100.

In the absence of energetic interactions between B groups (εBB ≈ 0) and at a relatively weak B–B attraction, the dispersion σΩ is close to unity. It reflects that in this field, the bond vector r⃗AB could accept any directions. The dispersion σΩ decreases with the increase of |εBB|. First, it drops sharply; after that, it smoothly goes to plateau. The amplitude of the drop as well as its position depend on the macromolecular length N. For macromolecules with N = 100, the sharp drop of dispersion σΩ from σΩ ≈ π to σΩ ≈ 0.69π proceeds within the interval ΔεBB ≈ −1.5 ÷ −2.5. For macromolecules with N = 25, the interval of sharp drop shifts toward larger |εBB|: ΔεBB ≈ −3.0 ÷ −4.0; within this interval, the dispersion σΩ changes from σΩ ≈ 1 to σΩ ≈ 0.6. Inflection points of σΩ(εBB) dependence can be referred to as critical values ε1cr of transition from disordered to ordered state with prolonged aggregates. It is seen that the longer is macromolecular length N, the smaller is |ε1|.

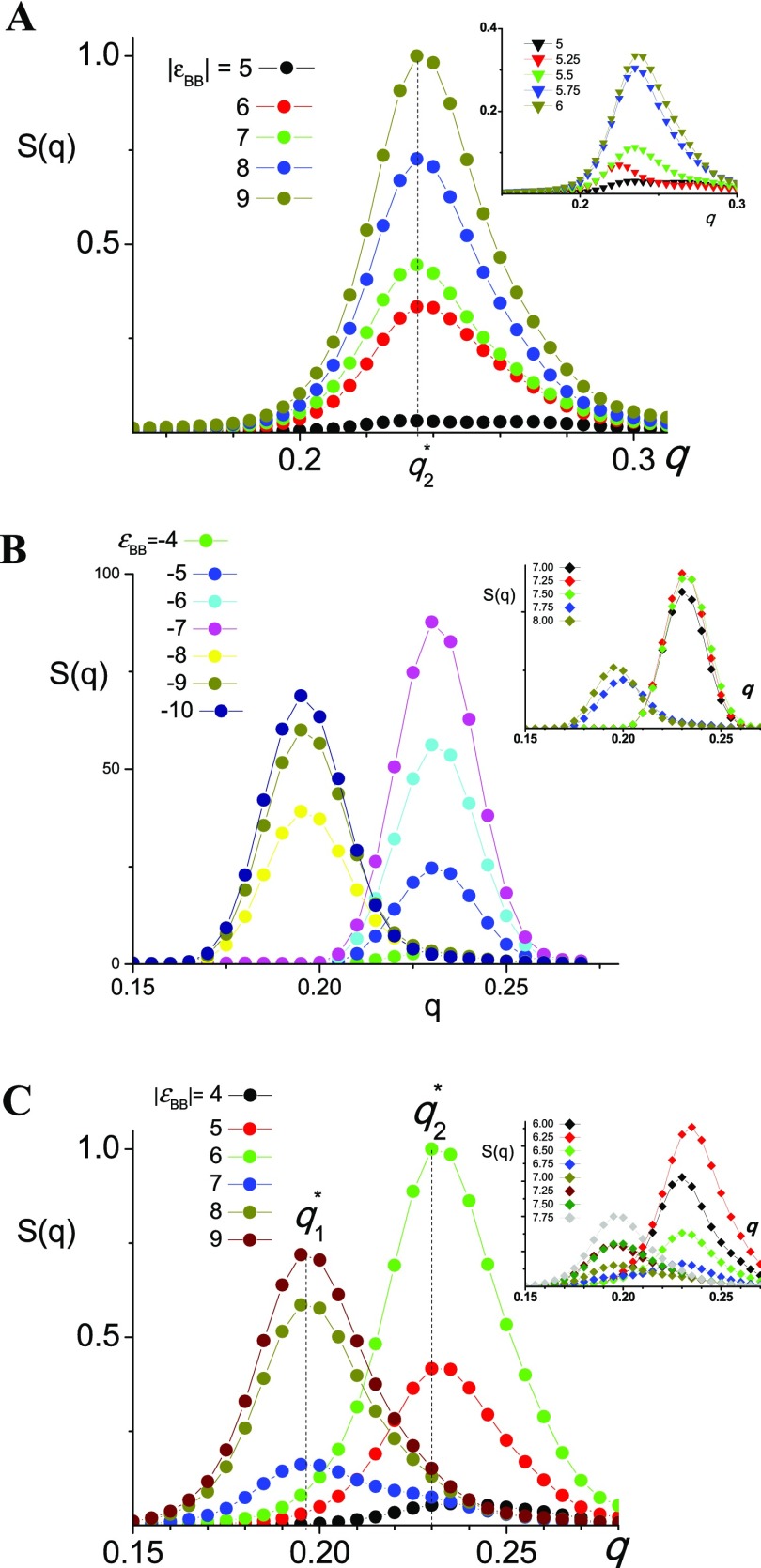
Figure 5 shows the structure factor S(q⃗) calculated according to the procedure of ref (49)

graphic file with name ao-2018-016438_m024.jpg

where r⃗ij is the vector between groups (i, j = 1, ..., 2nN); ei is −1 for A groups and +1 for B groups.

Figure 5.

Figure 5

Open in a new tab

Structure factor S(q) as a function of wave vector q for different energy εBB at N = 10 (A); 20 (B); and 50 (C).

Defined in that way, the structure factor S(q⃗) allows detecting the lamellar ordering and determining their domain spacing as: λ = 1/q*, where q* is the wave vector of the maximum of the structure factor.

It is seen in Figure 5 that the structure factor S(q⃗) can have pronounced maximum at two different values q1* ≈ 0.195 and q2 ≈ 0.23 indicating the existence of two types of lamellar structures with big λ1 ≈ 5 and small λ2 ≈ 4.35 domain spacing. The lamellae with small domain spacing are observed at the weaker εBB attraction. The availability and height of the maxima depend on the energy εBB and polymerization degree N.

In case of macromolecules with N = 10, the structure factor S(q) has the only maximum at q ≈ 0.235. This maximum appears at |εBB| ≈ 5.5 and demonstrates steady growth with the increase of |εBB|. For N = 20, one can distinguish three characteristic regions. At |εBB| ≤ 4, the structure factor S(q) has no extreme point; within interval 4 ≤ |εBB| ≤ 7.5, the structure factor S(q) has a well-pronounced maximum at q2* ≈ 0.23. At |εBB| ≥ 7.75, the structure factor S(q) also has the only maximum located at a lower wave vector: q1 ≈ 0.195 (see Figure 5B and insert). Thus, within interval 7.5 <|εBB| < 7.75, the period of lamellae structure increases from λ2 ≈ 4.35 to λ1 ≈ 5. In case of longer macromolecules (N = 50), the transformation of lamellae proceeds within a much wider interval from |εBB| = 6.5 to |εBB| = 7.75. Within this interval, the structure factor has a broad maximum covering both q1* and q2 area and indicating the coexistence of lamellae with different domain spacing. Also, here the maximum value of the structure factor is much lower. Thus, the analysis of structure factors allows us to distinguish the field of lamellae with small spacing (the only distinct maximum at q2*), the field of lamellae with big period (the only distinct maximum at q1) and the transition region. For a given degree of polymerization N, the field of lamellae with a small period is limited by an energy interval εs–bcr < εBB < εs, where plot S(q) demonstrates the only maximum at the big wave vector. The boundary εbcr of lamellae with a big domain spacing field is determined as the maximum value of energy εBB having a structure factor with the only maximum at the small wave vector. The interval from εs–b to εbcr is the transition region which includes both lamellae structures joined with each other to single structure referred as the parking garage structure.31

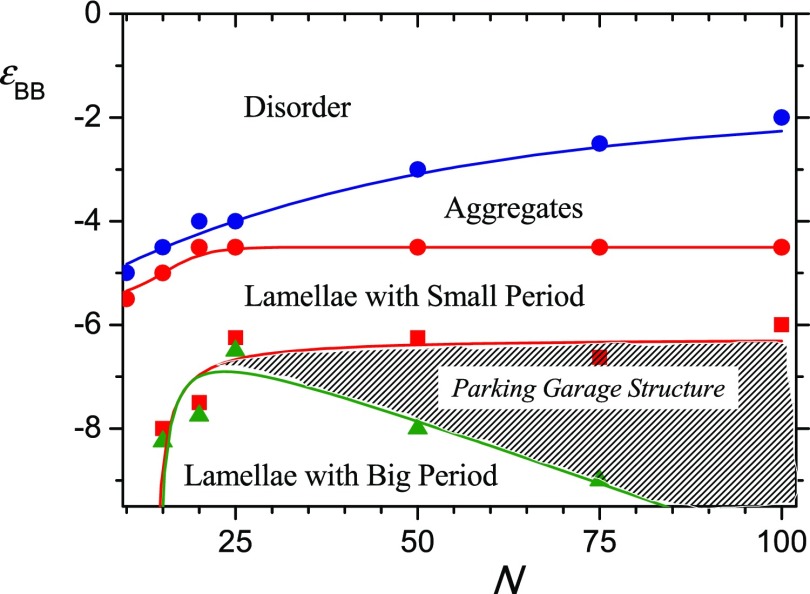
The results are summarized as a diagram of states in Figure 6. There, regions without segregation of A and B groups and with aggregates from few macromolecules, fields of lamellae with small and big domain spacing, and parking garage region are shown. The boundaries between different regions are calculated according to the procedures described above.

Figure 6.

Figure 6

Open in a new tab

State diagram. ε1cr (Inline graphic); εs (Inline graphic); εs–bcr (Inline graphic); and εb (Inline graphic).

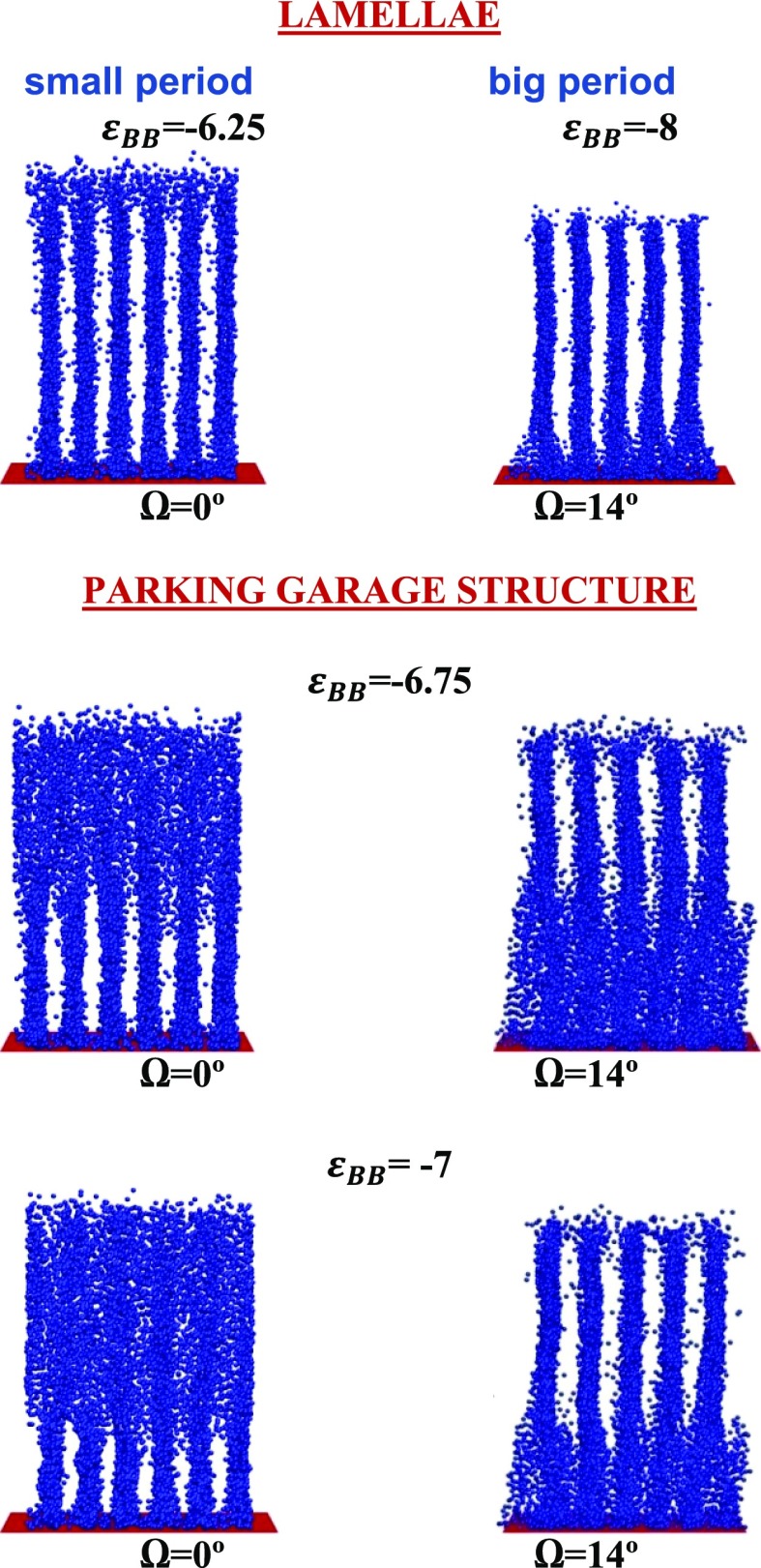
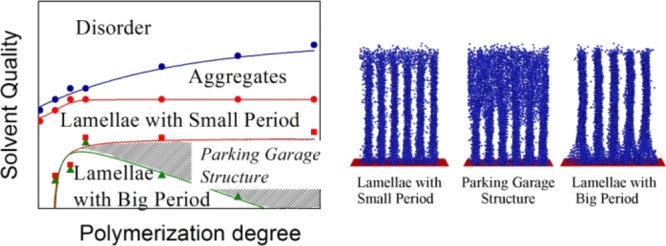
One can see that longer macromolecules undergo disorder-aggregates transition at the lower attraction between side groups. Curve, indicating the boundary between aggregates and region of lamellae with small domain spacing, is increasing function of N only at small polymerization degree (N < 20); then, it goes to plateau and remain constant. Another curve, limiting the region of lamellae with small domain spacing at high values of |εBB| also is parallel to N axis at N > 25. At smaller N (N < 25), it drops sharply. Our calculations show that macromolecules with N < 15 keep small domain spacing even at extremely high attraction εBB. Longer macromolecules join to lamellae with a small domain spacing at relatively small B–B attractive interaction (Figure 7, εBB = −6.25) and form lamellae with a big period at high attraction (Figure 7, εBB = −8). Boundary of the region of lamellae with a big domain spacing is shown by green. The shaded spacing between red and green curves is the transition region. It is extremely narrow for short macromolecules and broadens with the increase of polymerization degree N. In this transition region, the lamellae with different periods are piled one over the other (Figure 7, εBB: = −6.75 and −7): lamellae with big domain spacing are in the top of the brush and lamellae with small domain spacing are close to the grafting surface. In fact, they form a system of parallel layers mutually connected by bridges which are similar to the ramps in the multistorey parking garage31 (first, the term “parking garage structure” was employed to name a similar ordering in the endoplasmic reticulum with stacked membrane sheets and twisted membrane connection51).

Figure 7.

Figure 7

Open in a new tab

Instant snapshots taken from different angles Ω at different energies εBB. N = 50. Only side B groups are shown.

The formation of a parking garage structure embarks as the appearance of a thin layer of the lamellae with big domain spacing on the top of the brush (Figure 7). This layer is turned with respect to the bottom lamellae on an angle of 14°. To make it clear, we present instant snapshots in the front projection (Ω = 0) and in projection rotated by Ω = 14°. One can see that the bottom layer contains six lamellae which are parallel to the oX. Upper layer includes five lamellae. With the increase of |εBB|, this layer becomes thicker, it shifts closer to the grafting surface, and finally spreads to the whole grafting layer.

Short macromolecules (N < 25) pass through the parking garage structure within an extremely narrow interval of εBB. Long macromolecules with N = 100 persist parking garage structure even at a rather strong attractive interactions: εBB < −10.

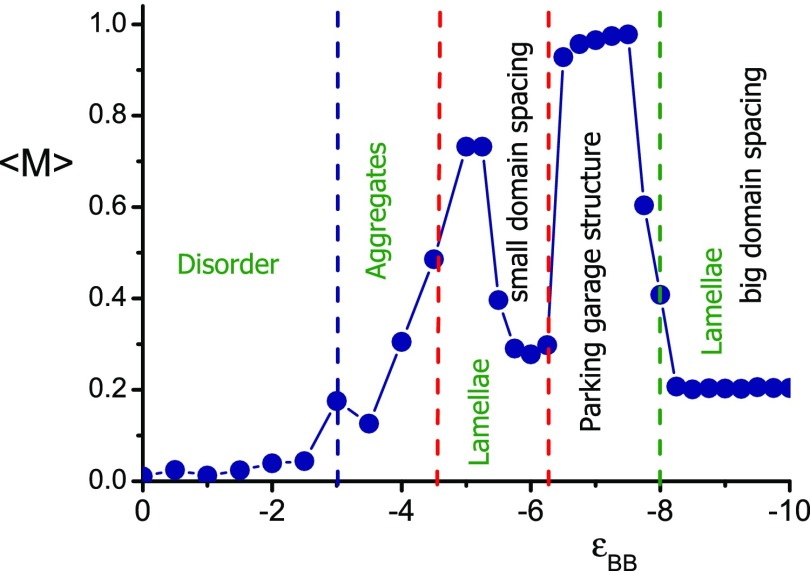
To reveal bicontinuous properties of the parking garage structure, the fraction ⟨M⟩ of B groups belonging to the largest aggregate was calculated. Aggregate is defined as a set of B groups, each within the distance rag = 1.3 from one or more other groups in the cluster. By definition, ⟨M⟩ changes within the interval 0 < ⟨M⟩ ≤ 1 and reaches its maximum value when all B groups are joined into a single cluster. It is seen (Figure 8) that ⟨M⟩ is a complex function of εBB. First, it monotonously increases up to ⟨M⟩ ≈ 0.7, then drops to ⟨M⟩ ≈ 0.3, abruptly goes to ⟨M⟩ ≈ 1, and finally undergoes a sharp transition to ⟨M⟩ ≈ 0.2. It is seen that sharp changes in ⟨M⟩ are the consequence of structure reconstruction. The boundaries of structure are shown by a dashed line colored in accordance with the state diagram in Figure 6. Aggregation number ⟨M⟩ reaches its largest possible value in the region of the parking garage structure where ⟨M⟩ = 1. In that way, we numerically confirm the bicontinuous character of parking structure with all B groups joined in the single cluster.

Figure 8.

Figure 8

Open in a new tab

Fraction ⟨M⟩ of B groups at the biggest aggregate as a function of εBB. N = 50.

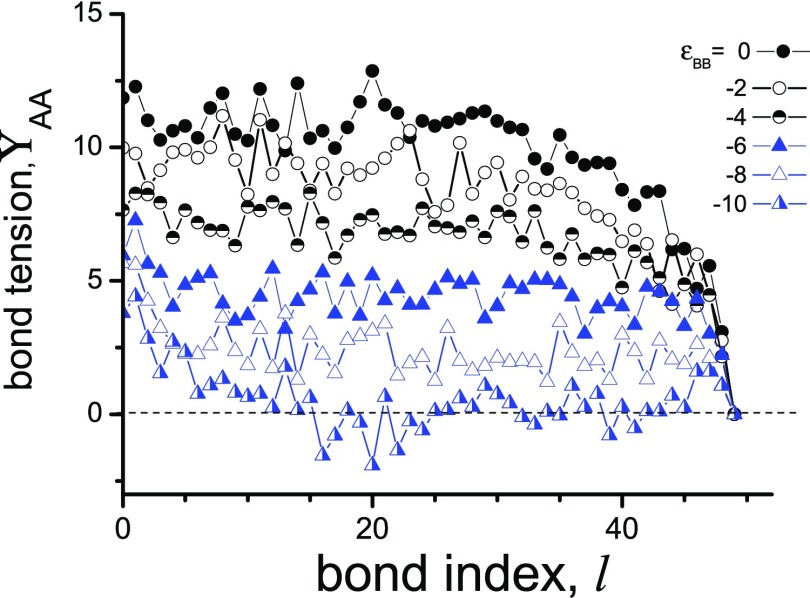
The significant stretching of macromolecules caused by their dense grafting leads to substantial backbone tension ΥAA.52,53 Backbone tension ΥAA(l) of the l bond (l = 1, ..., N – 1) is a total force acting between l and l + 1 monomer units and determined by excluded volume (1) and FENE (2) potentials. The backbone tension ΥAA(l), averaged over chains and time, is shown in Figure 9 for different εBB.

Figure 9.

Figure 9

Open in a new tab

Backbone tension ΥAA as a function of bond index l for N = 50 and different energies εBB.

It is seen that one could distinguish two characteristic scenarios of ΥAA(l) dependencies. In the absence of attractive interaction and for relatively weak attraction (−4 ≤ εBB ≤ 0), the backbone tension ΥAA(l) is high. It is almost constant for the initial, closest to the grafting surface, part of macromolecules, and sharply declines with the increase of l for the ending part of the chain. It is seen here that the tension of starting part of macromolecules decreases with the increase of B–B attraction (the increase of absolute value |εBB|), and that even bonds in the external part (l = 47 and 48) are exposed to significant tension. In contrast, at stronger attractive interaction εBB ≤ −6, the backbone tension ΥAA(l) sharply decreases at the initial part of the chain, and then it stays as a constant. Here also, the backbone tension ΥAA(l) decreases with |εBB| growth. At εBB ≈ −10, the backbone tension ΥAA takes zero and negative values.

It means that in this case, the A–A bonds could be stretched (ΥAA > 0), shrunken (ΥAA < 0), or have precisely an equilibrium length (ΥAA = 0). It is seen that in fact only the initial part (l < 15) is stretched (ΥAA > 0), and the tension in the ending part (l > 15) fluctuates around zero. Our calculations reveal that even at the highest overall tension (εBB = 0), the average bond length expands by less than 1% from its equilibrium value: b = 0.97. In case εBB ≈ −10, fluctuations in the length of bond with index l > 15 are about 0.05%, and one can conclude that at εBB = −10, the bonds of ending part of macromolecules are close to their basic states with b = 0.97. Thus, the self-organization in densely grafted layers relieves the bond tension and diminishes the corresponding energy.

Conclusions

By means of computer modeling, we study the self-organization of macromolecules densely grafted to plane (polymer brushes) with surface-active monomers and different polymerization degree. The surface activity of monomers was accounted for by representing them as an A-graft-B “dumbbells” of two beads. A and B beads repel each other and selectively interact with the solvent. The solvent being athermal for backbone A groups and poor for pendant B, graduate worsening of the solvent quality, modeled by the increase of attractive B–B energy εBB, leads to aggregation of B groups and transformation of polymer brushes from the state with homogeneous A and B distribution to prolonged aggregates and lamellae structures. The plane of the lamellae is perpendicular to the grafting surface. The lamellae could have two different domain spacing: smaller in a less poor solvent and bigger in a more poor solvent. The domain spacings of both lamellae structures, if they arise, do not depend on the polymerization degree. In the transition region, these lamellae coexist but reside at different heights. Lamellae with small domain spacing are closer to the grafting surface and lamellae with large domain spacing are on the top. They are turned with respect to each other and are connected by twisted bridges to form the parking garage structure. The results are presented as a state diagram with five different regions: disorder, aggregates, lamellae with small domains spacing, transition region, and lamellae with big domain spacing. The boundaries were determined qualitatively through the calculations of the structure factor function, the circular distribution of A–B bond vectors, and its dispersion.

The boundary between disorder region and aggregates is monotonically an increasing function of polymerization degree: the longer are the macromolecules, the poorer is the solvent quality of aggregate formation. The position of the border between the region of aggregates and the region of lamellae with a small period does not depend on the polymerization degree for a sufficiently long chain (N > 25) and shifts toward poor solvent quality with the decrease of chain length N for shorter chains (N < 25). The width of the transition region between lamellae with different spacing depends on the polymerization degree: it is the widest for long macromolecules, narrows down with the decrease of macromolecular length, and totally disappears for relatively short macromolecules (N < 15). The reduced density of macromolecules was quite high (from 8.2 to 82), and macromolecules are stretched perpendicular to the grafting surface. This stretching is a result of excluded volume interaction with neighbor chains and induces sufficient backbone tension which is distributed over chains and depends on solvent quality. In the absence or at the relatively weak B–B attraction (disordered or aggregates regions in state diagram), the dependence of bond tension on bond index looks similar to a step function: the bond tension is constant which does not depend on the bond index for the whole chain except short outer piece, where tension drops sharply. At strong B–B attraction (lamellae and parking garage structure), the repulsive excluded volume interactions are screened and bond tension as a whole is smaller, and maximum tension is imposed on the bond next to grafting surface. It can be explained by larger scale of emerging structures that leads to stretching of the beginning pieces of chains, the so-called legs. The stretching is balanced by energetic gains because of stronger aggregation of B groups and formation of sufficient room for A–B segregation. In short macromolecules, legs could comprise a significant part of the chain, and the shorter the chain, the larger interaction energy εBB is needed to counterbalance the stretching of legs. In extremely short macromolecules, such balance is unreachable at least for an investigated range of interaction energy εBB; thus, lamellae with a larger domain spacing do not appear at all.

The formation of different structures is accompanied by the change of B–B aggregation number which exhibits sharp jump in the region of “aggregates-lamellae” and “lamellae-parking structure-lamellae” transitions. For the parking garage structure, the aggregation number, measured as a fraction of monomer units entering the biggest clusters, is close to unity. It is the maximum possible value indicating the merge of all B groups to the only cluster and the formation of the bicontinuous structure. The ability to pass rapidly from bicontinuous to lamellae structure could be interesting for practical applications which require a quick change of connectivity, such as molecular switches, elements of electrical circuits, the system for controllable catalysis, and so forth.54 We believe that such types of reconstruction (lamellae—parking garage—lamellae) could be observed in other polymer systems, where self-organization is accompanied by the conformation changes of their constituent parts.

Acknowledgments

This research was supported financially by the Russian Science Foundation (project number 14-13-00745) and carried out in A.N. Nesmeyanov Institute of Organoelement Compounds of Russian Academy of Sciences. The research is carried out using the equipment of shared research facilities of HPC computing resources at Lomonosov Moscow State University.

The authors declare no competing financial interest.

References

  1. Brittain W. J.; Boyes S. G.; Granville A. M.; Baum M.; Mirous B. K.; Akgun B.; Zhao B.; Blickle C.; Foster M. D. Surface rearrangement of diblock copolymer brushes—stimuli responsive films. Adv. Polym. Sci. 2006, 198, 125–147. 10.1007/12_061. [DOI] [Google Scholar]
  2. Minko S. Responsive polymer brushes. J. Macromol. Sci., Part C: Polym. Rev. 2006, 46, 397–420. 10.1080/15583720600945402. [DOI] [Google Scholar]
  3. Zoppe J. O.; Ataman N. C.; Mocny P.; Wang J.; Moraes J.; Klok H.-A. Surface-initiated controlled radical polymerization: State-of-the-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. 10.1021/acs.chemrev.6b00314. [DOI] [PubMed] [Google Scholar]
  4. Klein J. Polymers in living systems: from biological lubrication to tissue engineering and biomedical devices. Polym. Adv. Technol. 2012, 23, 729–735. 10.1002/pat.3038. [DOI] [Google Scholar]
  5. Espinosa-Marzal R. M.; Bielecki R. M.; Spencer N. D. Understanding the role of viscous solvent confinement in the tribological behavior of polymer brushes: a bioinspired approach. Soft Matter 2013, 9, 10572–10585. 10.1039/c3sm51415c. [DOI] [Google Scholar]
  6. Halperin A.; Tirrell M.; Lodge T. P. Tethered chains in polymer microstructures. Adv. Polym. Sci. 1992, 100/1, 31–71. 10.1007/bfb0051635. [DOI] [Google Scholar]
  7. Pattanayek S. K.; Pham T. T.; Pereira G. G. Morphological structures formed by grafted polymers in poor solvents. J. Chem. Phys. 2005, 122, 214908. 10.1063/1.1917772. [DOI] [PubMed] [Google Scholar]
  8. Binder K.; Milchev A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci., Part B: Polym. Phys. 2012, 50, 1515–1555. 10.1002/polb.23168. [DOI] [Google Scholar]
  9. Alexander S. Adsorption of chain molecules with a polar head a scaling description. J. Phys. 1977, 38, 983–987. 10.1051/jphys:01977003808098300. [DOI] [Google Scholar]
  10. de Gennes P. G. Conformations of polymers attached to an interface. Macromolecules 1980, 13, 1069–1075. 10.1021/ma60077a009. [DOI] [Google Scholar]
  11. Brittain W. J.; Minko S. A structural definition of polymer brushes. J. Polym. Sci., Part A: Polym. Chem. 2007, 45, 3505–3512. 10.1002/pola.22180. [DOI] [Google Scholar]
  12. Williams D. R. M. Grafted polymers in bad solvents: octopus surface micelles. J. Phys. II 1993, 3, 1313–1318. 10.1051/jp2:1993202. [DOI] [Google Scholar]
  13. Zhulina E. B.; Birshtein T. M.; Priamitsyn V. A.; Klushin L. I. Inhomogeneous structure of collapsed polymer brushes under deformation. Macromolecules 1995, 28, 8612–8620. 10.1021/ma00129a021. [DOI] [Google Scholar]
  14. Zhulina E.; Singh C.; Balazs A. C. Behavior of tethered polyelectrolytes in poor solvents. J. Chem. Phys. 1998, 108, 1175–1183. 10.1063/1.475498. [DOI] [Google Scholar]
  15. Pattanayek S. K.; Pham T. T.; Pereira G. G. Morphological structures formed by grafted polymers in poor solvents. J. Chem. Phys. 2005, 122, 214908. 10.1063/1.1917772. [DOI] [PubMed] [Google Scholar]
  16. Lee T.; Hendy S. C.; Neto C. Tunable nanopatterns via the constrained dewetting of polymer brushes. Macromolecules 2013, 46, 6326–6335. 10.1021/ma400593z. [DOI] [Google Scholar]
  17. Semenov A. N. Contribution to the theory of microphase layering in block-copolymer melts. J. Exp. Theor. Phys. 1985, 61, 733–742. [Google Scholar]
  18. Borisov O. V.; Zhulina Y. B.; Birshtein T. M. Constitutional diagram and collapse of grafted chain layers. Polym. Sci. U.S.S.R. 1988, 30, 772–779. 10.1016/0032-3950(88)90188-8. [DOI] [Google Scholar]
  19. Skvortsov A. M.; Pavlushkov I. V.; Gorbunov A. A.; Zhulina Y. B.; Borisov O. V.; Pryamitsyn V. A. Structure of densely grafted polymeric monolayers. Polym. Sci. U.S.S.R. 1988, 30, 1706–1715. 10.1016/0032-3950(88)90393-0. [DOI] [Google Scholar]
  20. Yin Y.; Sun P.; Li B.; Chen T.; Jin Q.; Ding D.; Shi A.-C. A Simulated annealing Study of Diblock Copolymer Brushes in Selective Solvents. Macromolecules 2007, 40, 5161–5170. 10.1021/ma070393n. [DOI] [Google Scholar]
  21. Guskova O. A.; Seidel C. Mesoscopic simulations of morphological transitions of stimuli-responsive diblock copolymer brushes. Macromolecules 2011, 44, 671–682. 10.1021/ma102349k. [DOI] [Google Scholar]
  22. Jiang R.; Li B.; Wang Z.; Yin Y.; Shi A.-C. Self-assembled morphologies of diblock copolymer brushes in poor solvents. Macromolecules 2012, 45, 4920–4931. 10.1021/ma300564r. [DOI] [Google Scholar]
  23. Zhulina E. B.; Singh C.; Balazs A. C. Forming patterned films with tethered diblock copolymers. Macromolecules 1996, 29, 6338–6348. 10.1021/ma960498i. [DOI] [Google Scholar]
  24. Zhulina E. B.; Singh C.; Balazs A. C. Self-assembly of tethered diblocks in selective solvents. Macromolecules 1996, 29, 8254–8259. 10.1021/ma9606420. [DOI] [Google Scholar]
  25. Ferreira P. G.; Leibler L. Copolymer brushes. J. Chem. Phys. 1996, 105, 9362–9370. 10.1063/1.472725. [DOI] [Google Scholar]
  26. Wang J.; Müller M. Microphase separation of diblock copolymer brushes in selective solvents: Single-chain-in-mean-field simulations and integral geometry analysis. Macromolecules 2009, 42, 2251–2264. 10.1021/ma8026047. [DOI] [Google Scholar]
  27. Wang J.; Müller M. Memory Effects of diblock copolymer brushes and mixed brushes. Langmuir 2010, 26, 1291–1303. 10.1021/la902438e. [DOI] [PubMed] [Google Scholar]
  28. Rudov A. A.; Khalatur P. G.; Potemkin I. I. Perpendicular domain orientation in dense planar brushes of diblock copolymers. Macromolecules 2012, 45, 4870–4875. 10.1021/ma300890w. [DOI] [Google Scholar]
  29. Lazutin A. A.; Govorun E. N.; Vasilevskaya V. V.; Khokhlov A. R. New strategy to create ultra-thin surface layer of grafted amphiphilic macromolecules. J. Chem. Phys. 2015, 142, 184904. 10.1063/1.4920973. [DOI] [PubMed] [Google Scholar]
  30. Larin D. E.; Lazutin A. A.; Govorun E. N.; Vasilevskaya V. V. Self-assembly into strands in amphiphilic polymer brushes. Langmuir 2016, 32, 7000–7008. 10.1021/acs.langmuir.6b01208. [DOI] [PubMed] [Google Scholar]
  31. Lazutin A. A.; Vasilevskaya V. V.; Khokhlov A. R. Self-assembly in densely grafted macromolecules with amphiphilic monomer units: diagram of states. Soft Matter 2017, 13, 8525–8533. 10.1039/c7sm01560g. [DOI] [PubMed] [Google Scholar]
  32. Okhapkin I. M.; Makhaeva E. E.; Khokhlov A. R. Two-dimensional classification of amphiphilic monomers based on interfacial and partitioning properties. 1. Monomers of synthetic water-soluble polymers. Colloid Polym. Sci. 2005, 284, 117–123. 10.1007/s00396-005-1342-1. [DOI] [Google Scholar]
  33. Okhapkin I. M.; Askadskii A. A.; Markov V. A.; Makhaeva E. E.; Khokhlov A. R. Two-dimensional classification of amphiphilic monomers based on interfacial and partitioning properties. 2. Amino acids and amino acid residues. Colloid Polym. Sci. 2006, 284, 575–585. 10.1007/s00396-005-1447-6. [DOI] [Google Scholar]
  34. Vasilevskaya V. V.; Khalatur P. G.; Khokhlov A. R. Conformational polymorphism of amphiphilic polymers in a poor solvent. Macromolecules 2003, 36, 10103–10111. 10.1021/ma0350563. [DOI] [Google Scholar]
  35. Hordyjewicz-Baran Z.; You L.; Smarsly B.; Sigel R.; Schlaad H. Bioinspired polymer vesicles based on hydrophilically modified polybutadienes. Macromolecules 2007, 40, 3901–3903. 10.1021/ma070347n. [DOI] [Google Scholar]
  36. Larin D. E.; Glagoleva A. A.; Govorun E. N.; Vasilevskaya V. V. Morphological diagram of amphiphilic H-graft-P macromolecules in poor solvent: Theory and computer experiment. Polymer 2018, 146, 230–241. 10.1016/j.polymer.2018.04.077. [DOI] [Google Scholar]
  37. Wang L.-H.; Wu T.; Zhang Z.; You Y.-Z. Unconventional transitions of poly(N-isopropylacrylamide) upon heating in the presence of multiple noncovalent interactions. Macromolecules 2016, 49, 362–366. 10.1021/acs.macromol.5b02106. [DOI] [Google Scholar]
  38. Vasilevskaya V. V.; Ermilov V. A. Computer simulation of macromolecular systems with amphiphilic monomer units: biomimetic models. Polym. Sci., Ser. A 2011, 53, 846–866. 10.1134/s0965545x11090148. [DOI] [Google Scholar]
  39. Mahalik J. P.; Muthukumar M. Simulation of self-assembly of polyzwitterions into vesicles. J. Chem. Phys. 2016, 145, 074907. 10.1063/1.4960774. [DOI] [PubMed] [Google Scholar]
  40. Kriksin Y. A.; Khalatur P. G.; Erukhimovich I. Y.; ten Brinke G.; Khokhlov A. R. Microphase separation of diblock copolymers with amphiphilic segment. Soft Matter 2009, 5, 2896–2904. 10.1039/b905923g. [DOI] [Google Scholar]
  41. Glagoleva A. A.; Vasilevskaya V. V.; Khokhlov A. R. Microphase separation in the melts of diblock copolymers composed of linear and amphiphilic blocks. Polym. Sci., Ser. A 2010, 52, 182–190. 10.1134/s0965545x10020124. [DOI] [Google Scholar]
  42. Glagoleva A.; Erukhimovich I.; Vasilevskaya V. Void microstructuring in lamellar phase of amphiphilic macromolecules. Macromol. Theory Simul. 2013, 22, 31–35. 10.1002/mats.201200056. [DOI] [Google Scholar]
  43. Glagoleva A. A.; Vasilevskaya V. V.; Khokhlov A. R. Adsorption of amphiphilic comb-shaped macromolecules on a patterned surface. Polym. Sci., Ser. A 2011, 53, 344–353. 10.1134/s0965545x11040031. [DOI] [Google Scholar]
  44. Glagoleva A. A.; Vasilevskaya V. V. Macromolecules with amphiphilic monomer units at interface of two immiscible liquids. J. Chem. Phys. 2017, 147, 184902. 10.1063/1.5001880. [DOI] [PubMed] [Google Scholar]
  45. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  46. Sadovnichy V.; Tikhonravov A.; Voevodin V.; Opanasenko V.. “Lomonosov”: Supercomputing at Moscow State University. In Contemporary High Performance Computing: From Petascale toward Exascale; Vetter J. S., Ed.; Chapman& Hall/CRC Computational Science; CRC Press: Boca Raton, USA, 2013; pp 283–307. [Google Scholar]
  47. Abraham F. F.; Singh Y. Structure of a hard-sphere fluid in contact with a soft repulsive wall. J. Chem. Phys. 1977, 67, 2384. 10.1063/1.435080. [DOI] [Google Scholar]
  48. Schneider T.; Stoll E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B: Condens. Matter Mater. Phys. 1978, 17, 1302–1322. 10.1103/physrevb.17.1302. [DOI] [Google Scholar]
  49. Arora A.; Morse D. C.; Bates F. S.; Dorfman K. D. Commensurability and finite size effects in lattice simulations of diblock copolymers. Soft Matter 2015, 11, 4862–4867. 10.1039/c5sm00838g. [DOI] [PubMed] [Google Scholar]
  50. Fisher N. I.Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, U.K., 1995. [Google Scholar]
  51. Terasaki M.; Shemesh T.; Kasthuri N.; Klemm R. W.; Schalek R.; Hayworth K. J.; Hand A. R.; Yankova M.; Huber G.; Lichtman J. W.; Rapoport T. A.; Kozlov M. M. Stacked endoplasmic reticulum sheets are connected by helicoidal membrane motifs. Cell 2013, 154, 285–296. 10.1016/j.cell.2013.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Sheiko S. S.; Panyukov S.; Rubinstein M. Bond tension in tethered macromolecules. Macromolecules 2011, 44, 4520–4529. 10.1021/ma200328h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Leuty G. M.; Tsige M.; Grest G. S.; Rubinstein M. Tension amplification in tethered layers of bottle-brush polymers. Macromolecules 2016, 49, 1950–1960. 10.1021/acs.macromol.5b02305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Dübner M.; Naoum M.-E.; Spencer N. D.; Padeste C. From pH- to Light-Response: Postpolymerization Modification of Polymer Brushes Grafted onto Microporous Polymeric Membranes. ACS Omega 2017, 2, 455–461. 10.1021/acsomega.6b00394. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES