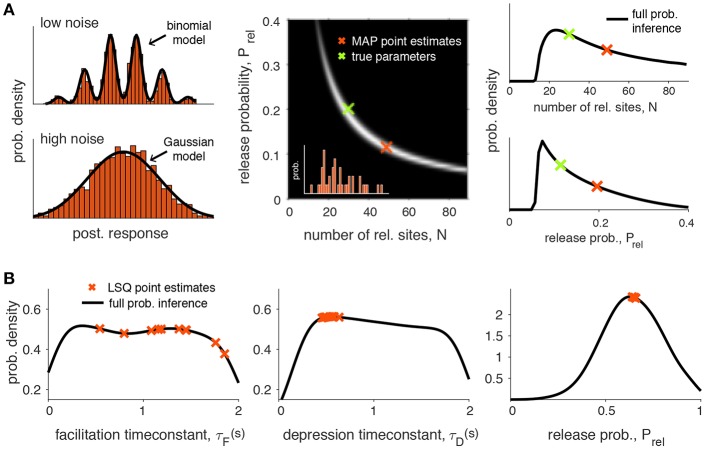
Figure 2.

Identifiability of synaptic transmission parameters. (A) Identifiability issues of quantal release models. Left upper figure: Histogram of 2000 simulated postsynaptic responses with N = 5, P_rel = 0.5, q = 1, σ = 0.3. In this case it is possible to fit a binomial model. Left lower figure: same simulation, but for high noise (σ = 0.7). The quantal peaks (i.e., the parameter N) are not identifiable anymore if the recording noise is too high, and in this case a Gaussian model provides a better description of the synaptic responses. Middle panel: Pairwise posterior marginal for N and P_rel for a typical experimental case with 40 observations (simulated postsynaptic responses shown in inset) where the true parameters were N = 30, P_rel = 0.2 and q = 1 (green cross). The maximum a posterior (MAP) estimates is obtained for N = 49 and P_rel = 0.11 (red cross): as N and p are anticorrelated, the posterior is roughly the same over a long band were N and p can be substituted, leading to inference error for a small number of observations. Right panel: Marginal posterior for N and P_rel from the previous panel. (B) Identifiability issues of short-term synaptic plasticity models. Given experimental data it is often of interest to infer the synaptic parameters. Two main types of inference have been applied: point estimations where a single scalar is estimated for one or more parameters (red crosses) or full probabilistic inference, where the full probability density over the parameters is obtained (black line). This particular example was obtained by inferring the Tsodyks-Markram model with four parameters given short-term plasticity recordings between pyramidal cells in layer-5 visual cortex (see Costa et al., 2013 for more details, only three parameters are shown here for simplicity: τ_F, τ_D and P_rel). Point estimates were obtained using a standard least-square (LSQ) fitting method (simulated annealing). Full probabilistic inference was done using MCMC sampling following Costa et al. (2013) (see main text for more details). As demonstrated by Costa et al. (2013) the uncertainty over the parameters can be greatly reduced by using more informative protocols that cover a wider frequency range.