Mechanistic dose–response modelling of animal challenge data shows that intact skin is a crucial barrier to leptospiral infection

Abstract

Leptospirosis is a widespread and potentially life-threatening zoonotic disease caused by spirochaetes of the genus Leptospira. Humans become infected primarily via contact with environmental reservoirs contaminated by the urine of shedding mammalian hosts. Populations in high transmission settings, such as urban slums and subsistence farming communities, are exposed to low doses of Leptospira on a daily basis. Under these conditions, numerous factors determine whether infection occurs, including the route of exposure and inoculum dose. Skin wounds and abrasions are risk factors for leptospirosis, but it is not known whether broken skin is necessary for spillover, or if low-dose exposures to intact skin and mucous membranes can also cause infection. To establish a quantitative relationship between dose, route and probability of infection, we performed challenge experiments in hamsters and rats, developed mechanistic dose–response models representing the spatial dynamics of within-host infection and persistence, and fitted models to experimental data. Results show intact skin is a strong barrier against infection, and that broken skin is the predominant route by which low-dose environmental exposures cause infection. These results identify skin integrity as a bottleneck to spillover of Leptospira and underscore the importance of barrier interventions in the prevention of leptospirosis.

This article is part of the theme issue ‘Dynamic and integrative approaches to understanding pathogen spillover’.

1. Background

Much of the global burden of zoonotic disease is caused by familiar (and often neglected) zoonoses which remain difficult to control [1–3]. In particular, high-burden zoonotic pathogens, including many zoonotic protozoans and helminths, non-typhoidal Salmonella spp., Leptospira spp. and Toxoplasma gondii, are difficult to control because they persist well in environmental reservoirs and have ample opportunities for spillover into humans.

For environmentally persistent zoonotic pathogens, a complicated suite of factors governs spillover risk. Understanding the interplay between these factors is a crucial first step toward reducing human incidence. Upstream factors include the level of environmental contamination (in turn governed by disease ecology in the animal host population [4]), and human exposures to contaminated environments. These upstream factors determine the dose and route of exposure, which interact with host physical and immune defences to determine the probability that exposure leads to spillover [1]. Dose–response models quantify the relationship between the dose and the probability of infection, illness or death, for a given route of exposure [5–7]. By fitting these models to data from outbreaks or challenge studies, we aim to quantify the infectivity of a given pathogen, and the impact of underlying biological factors such as host traits, susceptibility or immune factors.

Leptospirosis is an emerging and neglected disease caused by spirochaetes of the genus Leptospira. In severe cases, leptospirosis can cause life-threatening symptoms including renal failure, haemorrhage and respiratory distress [8,9]. Leptospirosis is an environmentally transmitted zoonosis with a worldwide distribution, but the major burden is in impoverished populations [10]. The spirochaete can infect most mammalian hosts, and can be shed chronically by asymptomatic carriers [8,11]. Humans become infected after exposure to water or soil contaminated by the urine of infected animals, and Norway rats (Rattus norvegicus, hereafter referred to as rats) are the primary reservoir species in many urban settings [12,13]. A colony of infected rats can shed of the order of one billion leptospires per day [14], but leptospires do not persist at high densities in soil and water [15]. Thus, low-dose environmental exposures most likely cause the majority of infections.

Skin wounds have been associated with high risk of leptospirosis in humans [16] and in rats [14,17]. In humans, broken skin may directly increase the probability of zoonotic spillover by increasing the susceptibility of human hosts [18]. In rats, broken skin may increase the probability of zoonotic spillover indirectly by helping maintain high prevalence and shedding in a key reservoir species, and in turn, higher levels of environmental contamination [17]. To quantify how skin integrity affects the probability of infection, given exposure to a particular dose, we conducted experimental infections in hamsters and rats, in which we introduced a range of inoculum doses through intact, shaved or abraded skin, through the conjunctiva, and through the traditional intraperitoneal (IP) route. We then developed mechanistic dose–response models to quantify the protective effect of intact skin as a physical immune barrier against Leptospira.

2. Methods

(a). Experimental infections

All animals were infected with a virulent clinical isolate from Brazil [14,19], Leptospira interrogans serovar Copenhageni strain Fiocruz L1-130, with four and eight passages in vivo and in vitro, respectively. Leptospires were cultivated in liquid Ellinghausen–McCullough–Johnson–Harris (EMJH) medium [20] supplemented with 1% rabbit serum. The cultures were kept up to 7 days at 30°C, reaching a mid-log phase between 4 and 5 days of culture. Bacteria were counted in a Petroff–Hausser counting chamber (Fisher Scientific).

Experimental infections were performed with three-week-old male golden Syrian hamsters (Envigo). As previously described [21], groups of three to four hamsters were inoculated by intraperitoneal (IP) or conjunctival routes using different doses of strain Fiocruz L1-130, ranging from 10¹ to 10⁸ and from 10² to 10⁸ leptospires, respectively. For infections via the abraded skin route, groups of four hamsters were shaved over their flank 1 day before inoculation. On the day of challenge each animal among groups of four hamsters was anaesthetized with isoflurane by an open-drop method, and an approximately 3–4 cm² area of the flank skin patch was abraded by gentle scraping with a surgical scalpel blade enough to damage the epidermis stratum corneum, adopting a methodology previously described [19]. A 50 ml volume of EMJH with the respective dose of leptospires was inoculated over the abraded area, followed by immediate application of a transparent film dressing (Tegaderm, 3M) to cover and keep the inoculum in place for 5 min. After removing the dressing, the area was gently washed with distilled water. A similar procedure was performed in groups of four hamsters for the ‘shaved skin’, without the abrading, and ‘intact skin’, without the shaving and abrading. For the latter procedure, the inoculum was performed over the fur on the animal flank.

Experimental infections were also performed using three-week-old male Wistar rats (Envigo). Groups of two to three animals were inoculated by IP route or by abraded skin method as described above, using a dose range of 10¹–10⁸ leptospires.

Hamsters were monitored twice daily, and rats were monitored three times per week up to 21 days post-infection. Endpoints in hamsters included signs of disease and death [19]. Since infection is asymptomatic and causes persistent renal colonization in rats, we used lipL32-based qPCR [14] to evaluate presence of leptospiral DNA in their urine, as an endpoint. Surviving animals at the end of the experiment or moribund animals presenting with clinical signs of disease were immediately sacrificed by inhalation of CO₂. LD₅₀ (lethal dose, 50%, in hamsters) and CD₅₀ (colonization dose, 50%, in rats) were calculated as described previously [22].

(b). Mechanistic dose–response model

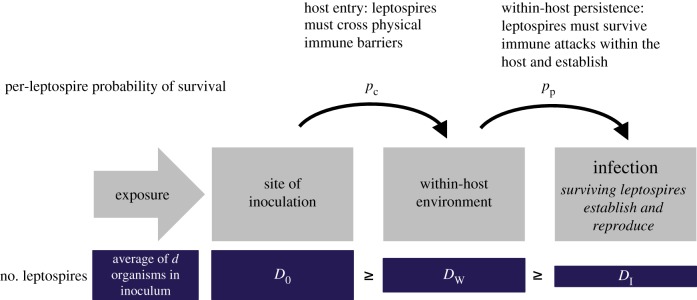
Once an infectious organism contacts a potential host (an event we term ‘exposure’ or ‘inoculation’), infection is a multi-step process in which the infectious organism must cross physical immune barriers like the skin or mucous membranes (host entry), and then survive attacks from innate or adaptive immune effectors within the host (within-host invasion and persistence). Established dose–response models, such as the exponential and beta-Poisson models [5], treat infection as a one-step process, in which each organism in the inoculum has some probability of surviving both steps and contributing to infection. To study the specific impact of intact skin as a physical immune barrier against host entry, we built on established methods to develop a two-step dose–response model that treated host entry and within-host invasion and persistence as distinct stochastic processes (figure 1).

Figure 1.

Model of infection process. Organisms introduced via intraperitoneal inoculation bypass the ‘host entry’ process. Quantity d is known from the measured concentration of bacteria in the inoculum stock solution. Quantities D₀, D_W and D_I are not observable. The model probabilistically considers all possible values of these unknown quantities. (Online version in colour.)

First, based on the measured bacterial concentration in the inoculum stock solution, the expected number of organisms, d, in each inoculum was known. But the exact number of organisms introduced to the host, D₀, could have been slightly higher or lower than the expected quantity d, and was not directly observable. Our models assumed the exact inoculum dose, D₀, followed a Poisson distribution with mean d.

Next, we assumed each infectious organism in D₀ had an equal and independent probability, p_c, of crossing physical immune barriers at the site of inoculation, and that D_W organisms successfully reached the within-host environment. Then, we assumed organisms that successfully entered the host had a second fixed and independent probability, p_p, of successfully invading and persisting as part of an established infection. D_I represented the number of organisms that survived both steps and became founders of an active infection. These assumptions imply the number of organisms successfully reaching the within-host environment, D_W, and the number of organisms establishing within the host, D_I, were both distributed binomially, with P(D_W = k)∼B(D₀,p_c) and P(D_I = m)∼B(D_W,p_p). We assumed that inoculations via the IP route bypassed physical barriers, such that D_W = D₀.

Finally, we assumed infection would occur if one or more organisms survived to establish and reproduce within the host, i.e. if D_I > 0. An alternative hypothesis holds that the minimum infecting dose might be greater than 1, owing to a need for cooperation or collective defence among pathogenic organisms. However, the single-organism hypothesis has received more scientific support than the threshold hypothesis in other systems [5], and infection occurred consistently in IP experiments with expected dose, d, of only 10 leptospires, which definitively rules out the existence of a high threshold for Leptospira.

(c). Likelihood for IP inoculation experiments and estimation of p_p

Data from IP inoculation experiments enabled us to estimate p_p independently of the other unknown parameter, p_c. This step was necessary because parameters p_p and p_c occur as a product in the likelihood and hence are not identifiable (equation (2.6)). The probability of infection after IP inoculation with dose d was

$$P_{\mathrm{I}}(d)=\sum _{D_{\mathrm{I}}=1}^{\mathrm{\infty }}\sum _{D_0=D_{\mathrm{I}}}^{\mathrm{\infty }}\left[{\displaystyle \frac{d^{D_0}{\mathrm{e}}^{-d}}{D_0!}}\right]\hspace{0.17em}\left[\left(\begin{array}{c}{D}_0\\ D_{\mathrm{I}}\end{array}\right)p_{\mathrm{p}}^{D_{\mathrm{I}}}{(1-p_{\mathrm{p}})}^{D_0-D_{\mathrm{I}}}\right].$$ 2.1

The first bracketed factor describes the Poisson probability that the inoculum contained exactly D₀ organisms, and the second bracketed factor describes the binomial probability that D_I of D₀ organisms survived to initiate infection. Finally, since D₀ and D_I were not observable, we summed across all possible combinations of D₀ and D_I values at which infection could have occurred. The above equation is identical in form to the exponential dose response model, which simplifies as described by Haas et al. [5]:

$$P_{\mathrm{I}}(d)=1-{\mathrm{e}}^{-d{p}_{\mathrm{p}}}.$$ 2.2

We found the maximum-likelihood estimate (MLE), and 95% profile confidence interval of parameter p_p by fitting to data from IP infection trials. The likelihood was constructed from the binomial probability of observing I_d infected individuals out of N_d trials at a given dose, d:

$$\begin{array}{rl}& \mathcal{L}(I_{d\min },N_{d\min },\dots I_{d\max },N_{d\max }|p_{\mathrm{p}})\\ & ={\prod }_d\left(\begin{array}{c}{N}_d\\ I_d\end{array}\right)I^{P_{\mathrm{I}}(d)}{(1-I)}^{1-P_{\mathrm{I}}(d)}.\end{array}$$ 2.3

(d). Likelihood for other routes of inoculation and estimation of p_c, basic model

After estimating p_p, we found MLEs of parameter p_c for each tested route of inoculation. For non-IP routes of inoculation, the probability of infection was similar to that in equation (2.1), but with an extra binomial factor to account for the probability of crossing physical immune barriers at the site of inoculation:

$$\begin{array}{rl}{P}_{\mathrm{I}}(d)& =\sum _{D_{\mathrm{I}}=1}^{\mathrm{\infty }}\sum _{D_{\mathrm{W}}=D_{\mathrm{I}}}^{\mathrm{\infty }}\sum _{D_0=D_{\mathrm{W}}}^{\mathrm{\infty }}\left[{\displaystyle \frac{d^{D_0}{\mathrm{e}}^{-d}}{D_0!}}\right]\hspace{0.17em}\left[\left(\begin{array}{c}{D}_0\\ D_{\mathrm{W}}\end{array}\right)p_{\mathrm{c}}^{D_{\mathrm{W}}}{(1-p_{\mathrm{c}})}^{D_0-D_{\mathrm{W}}}\right]\\ & \times \left[\left(\begin{array}{c}{D}_{\mathrm{W}}\\ D_{\mathrm{I}}\end{array}\right)p_{\mathrm{p}}^{D_{\mathrm{I}}}{(1-p_{\mathrm{p}})}^{D_{\mathrm{W}}-D_{\mathrm{I}}}\right].\end{array}$$ 2.4

We simplified equation (2.4) using a strategy similar to Haas, Rose and Gerba's approach to simplification of the standard exponential dose–response model [5]. First, the equation can be algebraically rearranged as follows:

$$\begin{array}{rl}{P}_{\mathrm{I}}(d)& =\sum _{D_{\mathrm{I}}=1}^{\mathrm{\infty }}\left[{\displaystyle \frac{{(d{p}_{\mathrm{c}}{p}_{\mathrm{p}})}^{D_{\mathrm{I}}}{\mathrm{e}}^{(-d{p}_{\mathrm{c}}{p}_{\mathrm{p}})}\hspace{0.17em}}{D_{\mathrm{I}}!}}\right]\\ & \times \sum _{D_{0=}{D}_{\mathrm{W}}}^{\mathrm{\infty }}\left[{\displaystyle \frac{d{(1-p_{\mathrm{c}})}^{(D_0-D_{\mathrm{W}})}{\mathrm{e}}^{-d(1-p_{\mathrm{c}})}\hspace{0.17em}}{(D_0-D_{\mathrm{W}})!}}\right]\\ & \times \sum _{D_{\mathrm{W}}=D_{\mathrm{I}}}^{\mathrm{\infty }}\left[{\displaystyle \frac{{(d{p}_{\mathrm{c}}(1-p_{\mathrm{p}}))}^{D_{\mathrm{W}}-D_{\mathrm{I}}}{\mathrm{e}}^{-d{p}_{\mathrm{c}}(1-p_{\mathrm{p}})}}{(D_{\mathrm{W}}-D_{\mathrm{I}})!}}\right]\end{array}$$ 2.5

Above, each bracketed factor is a Poisson density, with means $d{p}_{\mathrm{c}}{p}_{\mathrm{p}}$, $d(1-p_{\mathrm{c}})$, or $d{p}_{\mathrm{c}}(1-p_{\mathrm{p}})$, respectively. The second two Poisson series conveniently sum to 1, and can be removed from the equation. The remaining part, ${\sum }_{D_{\mathrm{I}}=1}^{\mathrm{\infty }}[{(d{p}_{\mathrm{c}}{p}_{\mathrm{p}})}^{D_{\mathrm{I}}}{\mathrm{e}}^{(-d{p}_{\mathrm{c}}{p}_{\mathrm{p}})}/D_{\mathrm{I}}!],$ can be re-written as the Poisson probability that D_I takes any value other than 0:

$$P_{\mathrm{I}}(d)=1-{\mathrm{e}}^{(-d{p}_{\mathrm{c}}{p}_{\mathrm{p}})}.$$ 2.6

We substituted the definition of P_I(d) from equation (2.6) into the likelihood given in equation (2.3). We then found maximum-likelihood estimates and 95% profile confidence intervals of parameter p_c by fitting to data from each tested route of inoculation (intact skin, shaved skin, abraded skin and conjunctiva).

(e). Likelihood for other routes of inoculation and estimation of α, β in the mixture model

The basic model introduced above assumed the per-leptospire probability of crossing physical immune barriers at the site of inoculation, p_c, did not vary among individual subjects. This assumption was reasonable for inoculation of intact skin or the conjunctiva, in which there was minimal potential for random, host-to-host variation in the integrity of physical immune barriers. However, even when using a carefully controlled experimental procedure, imperceptible, random variation in the depth of abrasions could have caused host-level variation in the skin's resistance to leptospires. We developed a more complex model (referred to as the mixture model) to test whether p_c varied meaningfully across hosts with abraded skin. Note that the mixture model is a two-step extension of the established beta-Poisson dose–response model described in [5].

In the basic model, p_c took a single, constant value for all hosts, whereas in the mixture model, probability p_c was treated as a random variable, with values in individual hosts following a beta distribution, i.e. p_c ∼ beta(α,β). Fitted parameters α and β determined the shape of this distribution of p_c values, and in turn, characterized the shape of host-to-host variability in the abraded skin's resistance to leptospires. Under the mixture model, the dose-specific probability of infection was

$$P_{\mathrm{I}}(d)=1-{\int }_0^1{\mathrm{e}}^{(-d{p}_{\mathrm{c}}{p}_{\mathrm{p}})}\left[{\displaystyle \frac{{(p_{\mathrm{c}})}^{\alpha -1}{(1-p_{\mathrm{c}})}^{\beta -1}}{\mathrm{beta}(\alpha ,\beta )}}\right]\mathrm{d}{p}_{\mathrm{c}}.$$ 2.7

Above, the bracketed factor is the beta(α,β) probability density describing the distribution of p_c values. We integrated across all possible p_c values to obtain the total probability of infection. The integral in equation (2.7) was solved numerically using the integrate() function in R.

The mixture model likelihood followed the same definition as in equation (2.3), but with equation (2.7) specifying P_I(d), and with two free parameters, α and β, replacing the single free parameter p_c.

(f). Code availability

All data analysis was performed in R [23], and all code used for data cleaning and import, data analysis, parameter estimation and plotting is freely available at https://zenodo.org/badge/latestdoi/171368954.

3. Results

(a). Infection experiments

A summary of the animal experiments is provided in table 1, whereas electronic supplementary material, table S1 presents the full data with corresponding values of LD₅₀ and CD₅₀. Our results are consistent with previous findings that L. interrogans strain Fiocruz L1-130 had a low LD₅₀ (approx. 10 bacteria) [17] when hamsters were infected by the IP route, while the strain had a lower CD₅₀ (approx. 10³ bacteria) than previously reported (10⁴ bacteria) when rats were infected by the IP route [24]. Of note, the abraded skin model showed similar results to IP route in hamsters and rats, with LD₅₀ and CD₅₀ between 10² and 10³ leptospires. By contrast, the strain had an LD₅₀ between 10⁶ and 10⁷ when hamsters were inoculated by the conjunctival route, which was similar to the LD₅₀ observed when inoculations were administered on shaved intact skin. Furthermore, a high infecting inoculum dose (10⁸ bacteria) was required to cause death in hamsters when inoculations were administered on unshaved intact skin. Taken together, those results indicated that intact skin is a major barrier against leptospiral infection in both acute hamster and chronic rat animal models for leptospirosis. Moreover, a simple abrasion of the epidermis reduced the LD₅₀ by an average factor of 10⁴.

Table 1.

Experimental outcomes.

route	dose	hamsters			rats
		n	lethality	%	n	colonization	%
intact skin	104	4	0	0.0
	106	8	0	0.0
	107	4	0	0.0
	108	8	2	25.0
shaved skin	104	4	0	0.0
	106	8	2	25.0
	107	4	3	75.0
	108	8	5	62.5
abraded skin	101	12	5	41.7	3	0	0.0
	102	12	8	66.7	5	0	0.0
	103	12	10	83.3	2	2	100.0
	104				6	6	100.0
	106				3	3	100.0
	108				4	4	100.0
conjunctiva	102	4	0	0.0
	103	4	0	0.0
	104	8	0	0.0
	105	12	0	0.0
	106	24	9	37.5
	107	20	14	70.0
	108	36	36	100.0
intraperitoneal	101	24	21	87.5	2	1	50
	5 × 101	4	4	100.0
	102	43	43	100.0	6	6	100.0
	2.5 × 102	12	12	100.0
	103	19	19	100.0
	104	28	28	100.0	3	3	100.0
	106	16	16	100.0	2	2	100.0
	108	3	3	100.0	6	6	100.0

(b). Estimated probabilities of host entry and within-host invasion and persistence

We used data from IP infection trials to estimate p_p, the probability that, after crossing physical immune barriers at the site of inoculation, each surviving leptospire established within the host and contributed to infection. The maximum-likelihood estimates were 0.21 (95% CI 0.12–0.36) in hamsters and 0.07 (95% CI 0.02–0.35) in rats (table 2).

Table 2.

Maximum-likelihood parameter estimates.

route	model	parameter	estimate	95% CI
hamsters
IP	all	pp	0.21	0.12–0.36
intact	basic	pc	1.29 × 10−8	2.14 × 10−9–4.17 × 10−8
shaved	basic	pc	9.54 × 10−8	4.57 × 10−8–1.86 × 10−7
abraded	basic	pc	0.02	0.01–0.04
	mixture	α	0.24	1.2 × 10−3–0.95
		β	0.40	1.0 × 10−3–8.47
conjunctival	basic	pc	8.43 × 10−7	5.25 × 10−7–1.35 × 10−6
rats
IP	all	pp	0.07	0.02–0.35
abraded	basic	pc	0.02	1.4 × 10−3–0.03
	mixture	α	no unique solutiona
		β	no unique solutiona

^aAs explained in the electronic supplementary, text, this maximum-likelihood estimate (MLE) was defined as a limit, and did not take a single fixed value. The pair (α = 1114.675, β = 50000.00) was used to approximate the MLE in figures 2b,d and 3e.

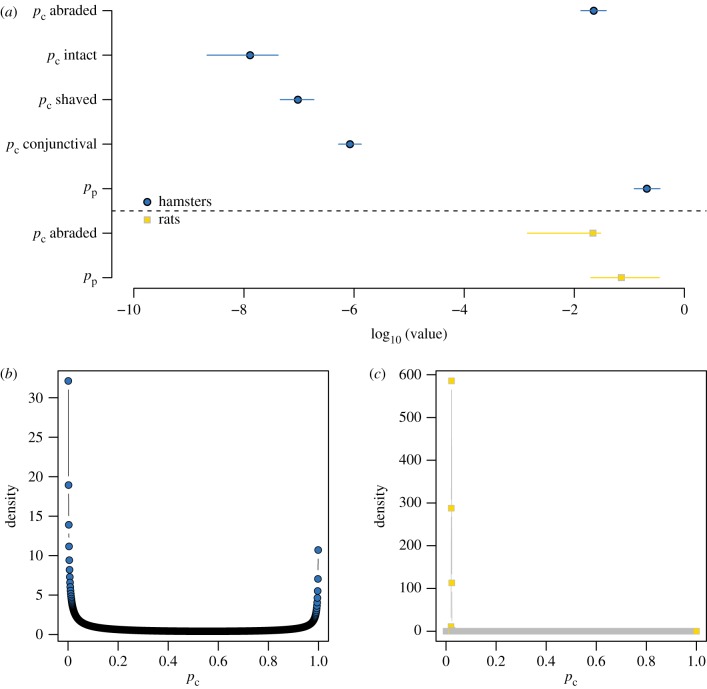
Next, we estimated p_c, the probability that any single leptospire was successful in host entry. Exact estimates and confidence intervals are reported in table 2 and figure 2. Abraded skin showed the weakest resistance to leptospires. The estimated per-leptospire chance of crossing abraded skin was about one in 50, whereas the estimated per-leptospire chances of crossing any intact barrier were never better than one in a million (conjunctiva), and for intact skin, about one in 77 million.

Figure 2.

Fitted parameter values. (a) Maximum-likelihood point estimates from the basic model of p_p and p_c, with 95% profile confidence intervals. The left-hand side of the x-axis represents probabilities closest to 0 (strongest immune barriers). (b) The mixture model returned a fitted distribution of p_c values, instead of a single point estimate. The distribution fitted to data from hamsters was strongly bimodal. (c) The distribution of p_c values fitted to data from rats asymptotically approached a Dirac delta function with all density at p_c = 0.02, corresponding to the estimate from the basic model (electronic supplementary material, text). (Online version in colour.)

(c). Impact of host-specific variability in abrasion depth

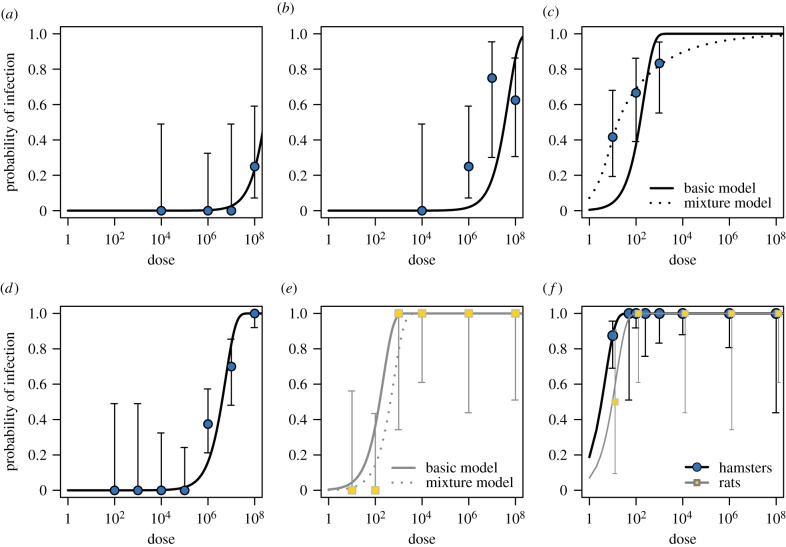
Initially, we assumed the per-leptospire probability of crossing the skin or mucosa (p_c) would be roughly equivalent for all individuals of the same species. Thus, p_c took a single, fixed value in the basic model, which provided good fits to most experimental data (figure 3). The one notable exception was the basic model's poor fit to data from experimental inoculation of hamsters with abraded skin (figure 3c).

Figure 3.

Model fits to data. Curves represent model-predicted probabilities of infection for each route of inoculation by dose, based on maximum-likelihood estimates. Routes of inoculation and study species: (a) hamsters, intact skin, (b) hamsters, shaved skin, (c) hamsters, abraded skin, (d) hamsters, conjunctiva, (e) rats, abraded skin, (f) both species, IP inoculation. Points and vertical bars represent experimentally observed infection frequencies, and 95% binomial confidence intervals calculated using the Wilson method. (Online version in colour.)

We hypothesized that the poor fit could have arisen if individual hamsters in fact showed different levels of resistance to leptospires, perhaps owing to microanatomical differences in the depth of their abrasions in the laboratory. To test this hypothesis, we built a more complicated model (the mixture model), which incorporated the possibility of hamster-to-hamster variability in the abraded skin's resistance to leptospires. This mixture model provided a much better fit to the data (ΔAIC (Akaike information criterion) = 25.47; figure 3c).

Within the mixture model, p_c did not take a single value. Instead, the model assumed p_c values followed a probability distribution from the beta family, whose shape was determined by fitted parameters α and β (table 2). This fitted distribution of p_c values can be interpreted as the distribution of individual hamsters' resistance to leptospires at abraded skin, with values closest to 1 representing the least resistance, (i.e. relatively severe abrasions).

The distribution of p_c values fitted to data from hamsters was bimodal, with the majority of density near extreme values 0 (does not cross abraded skin) and 1 (always crosses abraded skin) (figure 2b). The shape of this distribution suggests that even the narrow range of individual abrasion severity represented experimentally led to dramatic and measurable variation in the integrity of abraded hamster skin.

By contrast, data collected in rats showed no support for the mixture model over the basic model. In fact, when fitted to data from inoculation of abraded rat skin, the mixture model asymptotically approached the form of the basic model, with all density in the fitted distribution of p_c values concentrated in a spike near maximum-likelihood point estimate from the basic model (figure 2c; electronic supplementary material, text and figure S1). The shape of this distribution suggests there was negligible rat-to-rat variability in abraded skin's resistance to leptospires.

(d). Probabilities of infection given environmental exposure to a known dose

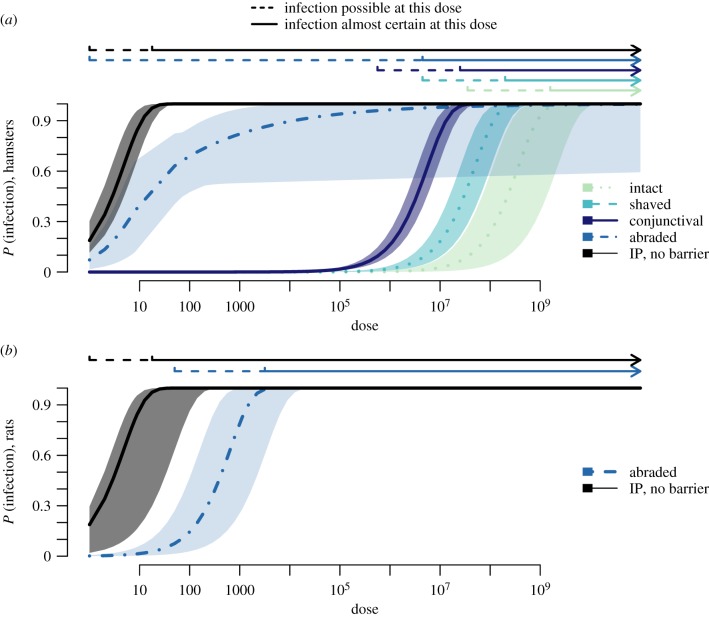
In natural settings, where hosts are likely to experience repeated, low-dose environmental exposures to Leptospira, probabilities of infection will depend on the route of exposure, as well as the intensity of environmental contamination. A comparison of probabilities of infection across various doses and various routes of exposure found that the probability that a low-dose exposure (d < 10⁵) causes an infection is greater than or equal to 10% only when the exposure occurs via abraded skin (figure 4). If exposure occurred via abraded skin, models predicted that an inoculum dose of a single leptospire had greater than or equal to 10% probability of causing an infection in hamsters, while as few as 50 leptospires had greater than or equal to 10% probability of causing an infection in rats (figure 4). In comparison, inoculum doses greater than 10⁵ leptospires were necessary for a conjunctival exposure to have a greater than or equal to 10% probability of causing an infection, and even higher doses were necessary given exposures at intact skin (figure 4).

Figure 4.

Model-estimated probabilities of infection, and confidence intervals for different routes of exposure. Estimates for (a) hamsters and (b) rats. The basic model was used to generate estimates, except for abraded skin in hamsters, where the best-fitting mixture model was used. Infection was considered possible for estimated probabilities of infection ≥ 0.1. Infection was considered almost certain for estimated probabilities of infection ≥ 0.975. (Online version in colour.)

4. Discussion

Our results provide experimental evidence that the relationship between broken skin and leptospirosis risk is causal, corroborating one previous study [19], and for the first time to our knowledge establish a quantitative relationship between dose and infection probability in the presence and absence of skin abrasions. Epidemiological studies previously associated broken skin with increased leptospirosis risk in humans [16] and in rats [14,17]. We showed the probability that a leptospire crosses physical immune barriers at most sites of inoculation was many orders of magnitude lower than the probability that a leptospire establishes infection once it reaches the within-host environment. Thus, intact skin and mucous membranes are the primary and crucial line of immune defence against Leptospira infection.

Intact skin showed strong resistance to leptospires. The per-leptospire odds of crossing intact skin were about one in 77 million (intact skin p_c = 1.29 × 10⁻⁸, table 2 and figure 2), and a dose of 10⁸ leptospires was necessary to cause infection if the inoculum was experimentally introduced to intact skin (table 1). For comparison, when physical immune barriers were absent (IP inoculation) or damaged (abraded skin), experimentally inoculated hosts became infected at doses as low as 10 leptospires. Parameter estimates from mechanistic dose–response models suggested that once leptospires cross physical immune barriers at the site of inoculation, they have excellent odds (better than one in 15, p_p ≥ 0.07) of persisting within the host and establishing infection. Furthermore, although mucosa is often described as a major point of entry for leptospires, our data showed that conjunctival mucosa is still an efficient barrier, emphasizing the importance of abrasion for leptospiral transmission.

The mixture model, which allowed for individual variation in abraded skin's resistance to leptospires, fitted the data from hamsters much better than the basic model. We were surprised to detect any measurable signal of individual variation in the resistance of abraded skin, as our experimental protocol would have allowed only imperceptible, microanatomical differences in abrasion depth across individuals. We suspect that hamsters' innate sensitivity to leptospirosis [25] may have helped magnify the impact of minor differences in abrasion severity. In contrast to results from hamsters, we found no signal of variation in the resistance of abraded skin across individual rats, a more resistant species (figure 2c; electronic supplementary material, text). Fewer experimental replicates in rats may also have dampened any signal of individual variation.

Given the innate sensitivity of hamsters, we interpret the signal of microanatomical variation in abrasion severity as a model for the impact of real-world variation in the size and depth of wounds in more resistant species. Given the bimodal distribution of fitted p_c values (figure 2b), the immunological impact of wounds does not appear to increase gradually with size and depth. Rather, the shape of the fitted distribution is consistent with the idea that some physiological threshold (in resistant species, perhaps breaking through the dermis, or damaging the microvasculature) distinguishes severe wounds from mild wounds. The fitted p_c distribution included considerable density near 1, indicating that severe wounds can render skin effectively useless as a barrier to infection. Even relatively mild abrasions showed surprisingly little resistance to leptospires. About 59% of p_c density fell at values greater that 0.1, which corresponds to a 10% chance or greater that leptospires successfully crossed abraded skin (figure 2b).

Overall, these findings have clear implications for the epidemiology of zoonotic spillover transmission and the epidemiology and prevention of leptospirosis. If intact human skin is a similarly effective barrier to infection, then exposures at sites of broken skin may cause the majority of naturally occurring infections in humans. Leptospira do not survive at high concentration in experimentally inoculated soil or water [15] and recent field studies confirmed that the leptospiral concentration in environmental sources, although ubiquitous, is relatively low [12,13]. Thus, real-world environmental exposures to high doses are likely to be rare.

We propose that, together, low infecting doses in the environment and the effectiveness of the intact skin barrier may not only limit the incidence of spillover, but may also limit the severity of infection when spillover does occur. Although leptospirosis can cause severe disease and death, most human cases are mild or asymptomatic [16,26]. In experimental animal models, exposure to higher doses and higher leptospiremia are associated with greater infection severity [21]. Thus, we speculate that the relatively high frequency of mild or asymptomatic cases in humans may be related to the high frequency of low-dose exposures in natural settings. Consistent with this hypothesis, severe cases or outbreaks are associated with floods and natural disasters (e.g. [27,28]), during which there is the risk of high-dose exposures, or overall exposure frequency may be elevated [12].

These results lend support to existing recommendations that using protective clothing and covering wounds and abrasions may dramatically reduce the risk of infection and symptomatic disease among people at high risk of Leptospira exposure [16]. Results suggest that covering even relatively mild skin abrasions may be beneficial. Follow-up studies should explore how much healing time is required before damaged skin regains the ability to act as an effective barrier against infection.

One limitation of our analysis was that we did not test the impact of repeated or extended exposures. In theory, dose-specific probabilities of infection might be lower with repeated, low-dose exposures if hosts develop adaptive immunity, or upregulate innate immunity over time [29]. Future experiments in rats, a resistant model for Leptospira infection, and a known maintenance species in urban settings, could clarify the impact of repeated exposures on dose–response relationships.

Practical and ethical constraints limited the number of experimental infections we performed, and the range of doses we were able to test. Ideally, the expected doses used in experimental infections would have spanned the full range of infection probabilities, from 0 to 1, for all tested routes of inoculation. However, our experience with these experiments shows that doses lower than 10 leptospires are impractical, and can yield experimental outcomes that are highly variable, biased or difficult to reproduce. We suspect this variability arises because with an expected dose, d < 10, stochastic variation in the actual number of organisms in the inoculum has strong impacts on infection outcomes. Furthermore, doses greater than 10⁸ are not relevant to the infecting doses found in the environment and responsible for spillover infections. For that reason, we made a technical and experimental decision to use 10 and 10⁸ leptospires as standard dose limits in our experiments, which in turn made it difficult to characterize the full dose–response curve for certain routes of infection. However, uncertainty around parameter estimates (figure 2a) and model-predicted probabilities of infection (figure 4) was lowest in cases where experimental data were available across the full range of infection probabilities (conjunctival inoculation in hamsters and abraded skin inoculation in rats).

Another major assumption of this analysis is that IP inoculation is the physiological equivalent of pathogens having penetrated the skin barrier. This assumption was motivated by previous work showing that leptospires introduced to abraded skin or via IP injection enter the bloodstream and spread with comparable speed and efficiency [19,21]. But differences in the local immune environments, or unmodelled physical barriers such as the peritoneal membrane, could lead IP infection data to slightly overestimate, or to slightly underestimate the value of p_p for other routes of exposure. Hypothetically, a subcutaneous injection experiment could help resolve additional details of the pathogen–host interaction. Importantly, our core finding, that abrasions dramatically decrease the skin's resistance to leptospires, follows from the relative estimates of p_c and is robust to this assumption.

This study analysed new experimental data with a mechanistic mathematical model to quantify dose–infection relationships for Leptospira interrogans, a globally important environmentally transmitted zoonotic pathogen. For the first time to our knowledge, our results quantified the importance of intact skin and mucous membranes as immune barriers against infection and show that wounds or abrasions can increase the risk of infection by many orders of magnitude. Our approach builds on a growing trend in microbial dose–response research, where models increasingly aim to incorporate mechanistic details of the within-host infection process [6,29]. It also exemplifies the crucial role of the dose–response relationship in shaping zoonotic spillover risk [1], and highlights the benefit of dissecting barriers to spillover for guiding disease control and prevention measures.

Ethics

All animal protocols were approved by the Institutional Committee for the Use of Experimental Animals, Yale University (protocol no. 2017-11424).

Data accessibility

All experimental data are available as an electronic supplementary data file. Code to perform all analyses and generate all figures, and published outputs are archived at https://zenodo.org/badge/latestdoi/171368954.

Authors' contributions

E.A.W. and A.I.K. conceived the study. E.A.W., V.B. and C.H. developed the experimental protocol and collected the data. T.R.J., J.O.L.-S. and K.M.G. developed the modelling methods. K.M.G. wrote the code and analysed the data with guidance from J.L.S. K.M.G. and E.A.W. drafted the manuscript. All authors critically revised the manuscript, gave final approval for publication and agree to be held accountable for the work described herein.

Competing interests

The authors declare no competing interests.

Funding

K.M.G. was supported by the Cota Robles Foundation, and the National Institutes of Health (F31AI134017, T32-GM008185). C.H. was supported by Programa Ciências sem Fronteiras, CNPq, Brazil. A.I.K. was supported by NIH grant nos R01AI052473, U01AI088752, R25TW009338, R01TW009504 and R01AI121207. J.O.L.-S. was supported by NSF grant nos OCE-1335657 and DEB-1557022, SERDP RC-2635 and DARPA PREEMPT D18AC00031.

Disclaimer

The content of the article does not necessarily reflect the position or the policy of the U.S. government, and no official endorsement should be inferred.