A Practical Guide to Variable Selection in Structural Equation Models with Regularized MIMIC Models

Abstract

Methodological innovations have allowed researchers to consider increasingly sophisticated statistical models that are better in line with the complexities of real world behavioral data. However, despite these powerful new analytic approaches, sample sizes may not always be sufficiently large to deal with the increase in model complexity. This poses a difficult modeling scenario that entails large models with a comparably limited number of observations given the number of parameters. We here describe a particular strategy to overcoming this challenge, called regularization. Regularization, a method to penalize model complexity during estimation, has proven a viable option for estimating parameters in this small n, large p setting, but has so far mostly been used in linear regression models. Here we show how to integrate regularization within structural equation models, a popular analytic approach in psychology. We first describe the rationale behind regularization in regression contexts, and how it can be extended to regularized structural equation modeling (Jacobucci, Grimm, & McArdle, 2016). Our approach is evaluated through the use of a simulation study, showing that regularized SEM outperforms traditional SEM estimation methods in situations with a large number of predictors and small sample size. We illustrate the power of this approach in two empirical examples: modeling the neural determinants of visual short term memory, as well as identifying demographic correlates of stress, anxiety and depression. We illustrate the performance of the method and discuss practical aspects of modeling empirical data, and provide a step-by-step online tutorial.

Introduction

The empirical sciences have seen a rapid increase in data collection, both in the number of studies conducted and in the richness of data within each study. With large numbers of variables available, researchers often seek to explore which variables explain observed variability beyond what their hypothesis-driven models attempted to confirm, identifying the variables that are most informative about the outcome of interest. Typical questions asked are: “What is the importance of my variables for predicting the outcome of interest?” and, ultimately, “What subset of variables is most predictive of (or most relevant for) my outcome?”

How to perform variable selection is a pervasive challenge in applied statistics. The field of statistical learning (also known as ‘machine learning’ or ‘data mining’) has dedicated a large amount of attention to the topic of how predictors can be optimally selected when there is little or no prior knowledge. Statistical approaches to variable selection range from the notorious stepwise variable selection procedures (cf. Thompson, 1995) to more complex and comprehensive approaches such as support vector machines or random forests. One particularly fruitful approach is that of regularized regression, a method that solves the variable selection problem by adding a penalty term that penalizes solutions, effectively producing sparse solutions in which only few predictors are allowed to be “active.” Regularization approaches vary in their precise specifications and include method such as Ridge (Hoerl & Kennard, 1970), Lasso (Tibshirani, 1996), and Elastic Net regression (Zou & Hastie, 2005).

Despite their strengths, these regularization approaches are generally developed in a context of models that only include observed indicators, which do not allow for modeling measurement error. However, incorporation of measurement error is central to many approaches in psychology. The most dominant approach to doing so in psychology and adjacent fields is the use of Structural Equation Modeling (SEM). SEM offers a general framework in which hypotheses can be formulated at the construct (latent) level with explicit measurement models linking the observed variables to latent constructs. Latent variable models account for measurement error, assess reliability and validity, and often have greater generalizability and statistical power than methods based on observed variables (e.g., Brandmaier, Wenger, Raz, & Lindenberger, submitted; Little, Lindenberger, & Nesselroade 1999). Here we describe a novel approach called regularized SEM, which incorporates the strengths of regularization into the SEM framework, allowing researchers to estimate sparse model solutions and implicitly solve large-scale variable selection in SEM by introducing a penalized likelihood function. We will use simulations and two empirical datasets (One from the Cambridge Study of Cognition, Aging and Neuroscience, in which we examine the neural determinants of visual short term memory, and a second from a large online sample measuring the Depression, Anxiety and Stress Scale; Lovibond & Lovibond, 1995) to illustrate the performance of regularized SEM, and discuss practical aspects of using the method for modeling empirical data. First we outline the general principles of regularization, how to extend these principles to SEM, and show how regularization is a viable and underused tool for settings with large numbers of predictors and relatively small sample sizes.

Regularization Overview

Regression

To set the stage for discussing the use of regularization (e.g. shrinkage or penalized estimation) in structural equation models, we give a brief overview in the context of regression. For more detail, interested readers may consult McNeish (2015) or Helwig (2017). We use ordinary least squares (OLS) estimation as a basis. Given N continuous observations of p predictors in matrix X and associated continuous outcome Y, we can estimate the regression coefficients by minimizing the residual sum of squares

$$RSS={\sum }_{i=1}^N(Y_i-{\beta }_0-{\sum }_{j=1}^p{\beta }_j{X}_{ij}){.}^2$$ (1)

For coefficients, we estimate an intercept β₀ along with β_j coefficients for each of the p predictors. However, there may be instances when we prefer a simpler model, namely a model that includes fewer predictors of the outcome. To perform variable selection we can use the Least Absolute Shrinkage and Selection Operator (Lasso; Tibshirani, 1996). Lasso regularization builds upon equation 1 above, incorporating a penalty for each parameter (with larger parameter values incurring a larger penalty):

$$Lasso=\underset{OLS}{\underbrace{RSS}}+\underset{Lasso}{\underbrace{\lambda {\sum }_{j=1}^p|{\beta }_j|.}}$$ (2)

The Lasso penalty includes the traditional RSS as in equation 1, but introduces two new components. First and foremost, it introduces a new penalty term that reflects the sum of all beta coefficients (righthand term in equation 2). In this manner, much like how a traditional regression attempts to minimize the squared residuals, the Lasso penalty also tries to drive parameters to zero, thus implicitly performing variable selection. Second, as can be seen in equation 2, the sum of the absolute value of each β_j coefficient is multiplied by a hyper-parameter, λ. This term λ quantifies the influence of the Lasso penalty on the overall model fit and thus weights the importance of the least-squares fit versus the importance of the lasso penalty - as λ increases, a stronger penalty is incurred for each parameter, which results in greater shrinkage of the coefficient sizes. λ is called a hyper-parameter because it cannot be estimated jointly with the β_j coefficients (this is not the case in Bayesian regularization, which we will return to later). As there is no generally optimal value for λ, it is common to test a range of λ values, combined with cross-validation, to examine what the most appropriate degree of regularization is for a given dataset. An additional type of regularization is Ridge regularization (Hoerl & Kennard, 1970), where in contrast to the Lasso, the Ridge sums the squared coefficients. Where the Lasso penalty will push the betas all the way to 0 (as any non-zero beta will contribute to the penalty term), the Ridge penalty will instead shrink betas, but not necessarily all the way to 0 (as the squaring operation means that small betas incur negligible penalties). One benefit of Ridge regularization is that it better handles multicollinearity among predictors. In an effort to combine both the variable selection aspects of the Lasso along with the ability to handle collinearity from Ridge regularization, Zou and Hastie (2005) proposed the Elastic Net. Through the use of a mixing parameter, α, the Elastic Net combines both Ridge and Lasso regularization

$$ElasticNet=RSS+\left(1-\alpha \right)\underset{Ridge}{\underbrace{\lambda {\sum }_{j=1}^p{\beta }_j^2}}+\alpha \underset{Lasso}{\underbrace{\lambda {\sum }_{j=1}^p|{\beta }_j|.}}$$ (3)

In the same way that it is common to test different values of λ, combined with cross-validation to choose a final model, the same can be done for α. Generally, this means testing values ranging from zero (equivalent to the Ridge penalty) to 1 (equivalent to the Lasso penalty).

Extensions

Originating from the application of ridge regression as a way to improve the results of OLS when predictors are correlated (Hoerl & Kennard, 1970), a large number of alternative forms of regularization have been proposed. In the case of high dimensional research scenarios, sparser versions of the lasso have been proposed. This includes the adaptive lasso (Zou, 2006), smoothly clipped absolute deviation penalty (Fan & Li, 2001), and the minimax concave penalty (Zhang, 2010), to name a few. Methods such as these have been shown to produce more optimal results when only a small number of predictors are desired to have non-zero coefficients among thousands or more candidate variables. In general, there is no optimal type of regularization as they each are optimal under different assumptions.

An additional way that regularization methods have been extended is with Bayesian estimation. In Bayesian regression, priors are placed on each of the coefficients in the model. When these priors are diffuse (large variances), the observed data has a large influence on the posterior distribution of each parameter. Regularization as applied to Bayesian estimation entails placing different types of prior distributions on those parameters of interest and constraining the prior variability to shrink the coefficients towards zero. Thus, prior knowledge, as applied through strong priors, carries greater weight in determining the posterior distribution for each parameter. Placing normal distributions priors has been shown to be equivalent to Ridge regression (Kyung, Gill, Ghosh, & Casella, 2010; Park & Casella, 2008; Tibshirani, 1996), whereas the Lasso corresponds to Laplace distribution priors (Park & Casella, 2008; Tibshirani, 1996). Particularly in the context where variable selection is desired, a number of more advanced forms of Bayesian regularization have been found to perform better (see van Erp, Oberski, & Mulder [2018] for an overview).

Regularization Rationale

Instead of the traditional use of a test statistic (and associated p-value) to determine the significance of a parameter, we instead test a sequence of penalties, use model comparison to choose a best fitting model, and examine whether the regression parameter estimates in this best model are non-zero. Non-zero coefficients can be thought of as important (e.g. see Laurin, Boomsma, & Lubke, 2016). This stands in stark contrast to the use of p-values, as using regularization to label parameters as important does not rely on any asymptotic foundations (it does not make statements with regards to a population). In particular, since the regularized estimates move away from the point of maximum likelihood, asymptotic distributions of parameter estimates do not hold anymore. Commonly paired with cross-validation, regularization attempts to identify which parameters are likely to be non-zero not only in the current sample, but also in a holdout sample.

One implicit conceptual assumption of regularization methods that set parameters to zero, such as the Lasso, is that of sparsity (e.g. Hastie, Tibshirani, & Wainwright, 2015) – in other words, it reflects the hypothesis that the true underlying model has few non-zero parameters. However, in psychological research, this is unlikely to be true. Instead, most variables in a dataset likely have small correlations among themselves (e.g. the “crud” factor; Meehl, 1990). As a result, the use of regularization in psychological research will impart some degree of bias into the results - as with all procedures, there is no such thing as a free lunch (Wolpert & Macread, 1997). Although this may first seem to be an undesirable side effect, we argue that there are common situations where the benefits of reduced variance outweigh the drawbacks of non-zero degrees of bias. First, we provide a brief overview of the bias-variance tradeoff.

Bias-Variance Tradeoff

Although regularization is often used in scenarios where variable selection is desired to achieve a parsimonious level of description, or where the number of predictors is larger than the sample size (P > N), one of the fundamental motivations behind regularization is in relation to the bias-variance tradeoff. Bias refers to whether our estimates and/or predictions are, on average (across many random draws from the population), equal to the true values in the population. Variance, on the other hand, refers to the variability or precision of these estimates (See Yarkoni & Westfall [2017] for further discussion). Practically speaking, we want unbiasedness and low variance (e.g., the Gauss-Markov theorem guarantees that least-squares estimation yields unbiased estimates with lowest variance among all unbiased linear estimators), however, both can be difficult to achieve in practice. Regularization plays a role in those scenarios where we wish to allow for some bias to achieve a larger decrease in variance. In cases where the sample size may be insufficient to adequately test the number of predictors we desire to include in our model, regularization will systematically bias the regression coefficients towards zero, as the variance of the estimator will be high due to the low sample size. Such an approach will prove particularly beneficial when the true model is sparse (ie., only few predictors are important).

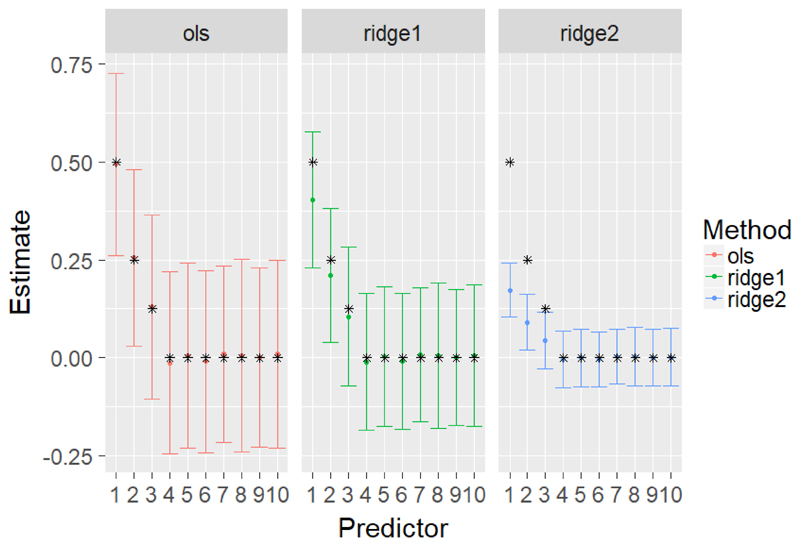
As a simple example, we simulated 30 observations with ten predictors of a normally distributed outcome variable, which is far below recommended guidelines for predictor to observation ratios in linear regression. Across 1,000 repetitions, the first predictor was simulated to have the strongest regression coefficient (0.5), the second was half as strong (0.25), and the third predictor was simulated as half of the second (0.125). The other seven predictors had simulated coefficients of zero. The resultant coefficients from both OLS and ridge regression models are display in Figure 1.

Figure 1.

OLS and Ridge regression (penalty of 5 for ridge1 and 50 for ridge2) parameter estimates. Asterisks denote the simulated parameter estimates. Error bars depict the standard deviation of the estimated parameters across 1000 repetitions.

In this, we can see unbiased estimates for OLS (the mean parameter estimates corresponding with the simulated parameter estimates [shown as asterisks]) However, this comes at the expense of variance, as there is a large degree of variability to the OLS coefficients. All of this is to be expected given methodological work on sample size recommendations for linear regression (Green, 1991). However, instead of restricting the number of predictors entered into the model based on the fixed sample size (only testing 2 predictors when really testing all 10 is desired), researchers can use regularization to impart bias as a mechanism to decrease the variance of the estimates. In contrast to the OLS results, the Ridge mean estimates are biased towards zero (i.e. the mean estimate is lower than the data generating mechanism), which becomes increasingly evident among larger simulated parameter estimates and penalty. Higher regularization imparts more bias towards zero, while also reducing the variance of the parameter estimates. Particularly in small sample sizes and/or when the number of variables is large (compared to N) this is a desirable property of regularization.

Rationale to Induce Bias

First, even though there may be a confluence of small effects in our dataset, we may not value the inclusion of every non-zero parameter into our model, as it complicates estimation and renders interpretation difficult. In this case we care more about what could be termed as functional sparsity, where we specifically aim to develop a parsimonious model that facilitates interpretation and generalization of the most important parameters. Second, one of the main motivations for the development of regularization methods is for datasets that have a larger number of variables than total observations. In this case, OLS regression cannot be used. Although settings where the number of parameters exceeds n may still be uncommon, the benefits generalize to settings where the ratio of observations to predictors is small, which can be construed as sample size challenge (e.g. Bakker, Van Dijk, & Wicherts, 2012). To achieve adequate power to detect a given parameter, a suitably large sample size (depending on the magnitude of the effect) is required. When multiple effects are considered, either separately or in the context of a multivariate model, the sample size to detect multiple effects can rapidly increase, reducing power. If collecting additional data is not possible for practical or principled purposes, one strategy for testing complex models in the presence of a small sample is to reduce the dimensionality of the model. Most commonly this means using some method such as stepwise regression to reduce the number of coefficients in a regression model, which can be highly problematic (e.g. Harrell, 2015).

Regularization in Structural Equation Modeling

In psychological research, it is common to have more than one outcome of interest, often specified as latent variables. Usually, researchers want to not only model a latent variable, but also predictors of these factors. One strategy is to estimate factor scores in a confirmatory factor analysis, extract the factor estimates and treat those as outcomes in a traditional OLS regression. However, this can be problematic (e.g. Grice, 2001, Devlieger & Rosseel, 2017), inducing issues such as biased estimates of the regression parameters and factor score indeterminacy. In contrast, one can stay within the latent variable framework, and include predictors of both outcomes of interest in a single analysis. This would allow for a richer set of analysis, allowing researchers to test equality of relationships across time, assess fit (through various fit indices), allow for directed relationships between latent variables, to name a few. Pairing regularization with a multivariate model of this type requires a generalization of the types of univariate regularization methods discussed prior.

Regularization has been extended in a number of directions beyond linear regression. This includes generalized linear models (e.g. Park & Hastie, 2007), network based models (e.g. Epskamp, Rhemtulla, & Borsboom, 2016), item response theory models (Chen, Li, Liu, & Ying, 2018; Sun, Chen, Liu, Ying, & Xin, 2016), differential item functioning (Magis, Tuerlinckx, & De Boeck, 2015; Tutz & Schauberger, 2015), educational assessment (Culpepper & Park, 2017), and factor analysis (e.g. Hirose & Yamamoto, 2015), to name just a few. Specific to our purposes is what we refer to as regularized structural equation modeling (RegSEM; Jacobucci, Grimm, & McArdle, 2016).

RegSEM directly builds in different types of regularization into the estimation of structural equation models, by expanding the traditional Maximum Likelihood estimation (MLE) to include a penalty term, as follows:

$$F_{regsem}=\underset{MLE}{\underbrace{\mathit{\text{log}}\left(\left|\Sigma \right|\right)+tr\left(C\ast {\Sigma }^{-1}\right)-\mathit{\text{log}}\left(\left|C\right|\right)-p}}+\underset{penalty}{\underbrace{\lambda P(\cdot )}}.$$ (4)

This adds a penalty term, λP(⋅) to the traditional MLE fit function. Just as in regularized regression, λ is the penalty, while P(⋅) is a general function for summing parameters. In the case of the Lasso, P(⋅) sums the absolute values of the specific parameter estimates. The same goal is accomplished for Ridge penalties, the Elastic Net, as well as other extensions (See Jacobucci, 2017). The other component of P(⋅) is selecting which parameters estimates should be included (i.e. which parameters are penalized). Because this form of regularization takes place in the estimation of structural equation models, regularization can be selectively applied to subset(s) of parameters, including factor loadings (e.g. subset selection in a questionnaire to create a short form), variances or covariances (e.g. test whether the addition of residual covariances is necessary) or, our specific interest, regression paths¹. For each of these penalized parameters in the model, it is important to standardize the corresponding variables prior to the analysis. By standardizing the variables, we ensure that each penalized parameter is equally weighted in contributing to model fit.

When the penalty term is either the Lasso or Elastic Net (or other sparse penalties), the number of effective degrees of freedom can change as the penalty increases. Most notably, as the penalty increases, each parameter that is set to zero increases the degrees of freedom (see Jacobucci, Grimm, and McArdle [2016] for additional information), thus often resulting in an improvement in fit with those fit indices that include the number of parameters in the equation (e.g. RMSEA, CFI, and information criteria). Note however, that some fit indices are derived under the assumption that the point estimate is maximum likelihood, thus, it may be preferable to evaluate test set prediction error rather than classic in-sample test statistics (see Yarkoni and Westfall, 2017).

RegSEM combines both confirmatory aspects of structural equation modeling with an exploratory search for important predictors. The confirmatory and exploratory aspects can take place in either the measurement or structural parts of a structural equation model. In many situations, researchers may have some a priori idea of how some variables relate to each other. To be more concrete, this may take the form of a confirmatory factor analysis (CFA) model. For instance, imagine a model with four indicators of a single latent variable such as fluid intelligence. This confirmatory formulation may be the result of previous research support for a single latent dimension underlying the covariance between all of the indicators. In contrast, we may have less certainty about which covariates in our dataset may be important predictors of the fluid intelligence latent factor, either because we lack strong a priori expectations, or because a large number of potential covariates is available (e.g. genetic markers, brain variables). As an example, Figure 1 displays the addition of three predictors (say, volumetric measures of different brain regions, cf. Kievit et al., 2014) to the initial CFA model resulting in a Multiple Indicator, Multiple Causes Model (MIMIC; Joreskog & Goldberger, 1975). Once the model is run, researchers commonly rely on traditional techniques such as the Wald test (and associated test statistics) to determine which predictors have non-zero population values. This kind of model is commonly used to simultaneously estimate the joint influence of a set of presumed causal influences on one or more latent variables. However, given the constraints of traditional SEM approaches, the predictors are usually selected a priori based on theoretical or empirical considerations (cf. Kievit et al., 2014). Now imagine an alternative scenario, instead of only incorporating a small set of predictors in a MIMIC model, researchers may have a much larger number of predictors they may wish to test (such as grey matter volume across all regions in an atlas). None of these additional relationships may be based on previous hypotheses. Instead, an exploratory search would be conducted. Here is where traditional tools are no longer as suitable, as the model may not converge, or estimates may be imprecise. This can be attributed to problems in using maximum likelihood estimation (MLE) with large numbers of variables when the sample size is limited (e.g. see Hastie,Tibshirani, & Wainwright, 2015). Although previous research has examined the influence of large models on test statistics (Yuan, Yang, & Jiang, 2017), less attention has been paid to strategies that produce more accurate parameter estimates. To address this challenge, we propose and evaluate the use of regularization to reduce the dimensionality of the model to improve the parameter estimate accuracy.

Combining what we have detailed with regularized regression, the rationale for using regularization, and regularization in structural equation models, we can now revisit our example in Figure 1. In going from the CFA model to the MIMIC model, we transition from a confirmatory latent variable model, based on previous research, to the inclusion of predictors that may not have a strong a priori basis. Moreover, in many applied fields such as genetics, cognitive neuroscience, epidemiology and similar fields, the ratio of predictors may be large compared to the available sample size. Indeed, one could argue that the absence of regularization methods may help explain why fields such as cognitive neuroscience rely on mass univariate approaches (i.e., a relationship between an outcome and neural data is tested thousands of times, separately for each brain region). However, as multivariate approaches generally paint a richer, more realistic picture of the true data structure, as well as allowing the researcher to investigate which effects are redundant across brain regions, and which may be partially independent complementary effects. To examine the possible benefits of regularization in the SEM context we conducted three studies. In Study 1 we examine the effectiveness of both MLE and regularization in the context of complex structural equation models. In Studies 2 and 3 we apply regularized SEM to a large existing datasets.

Study 1: Simulation

Methods

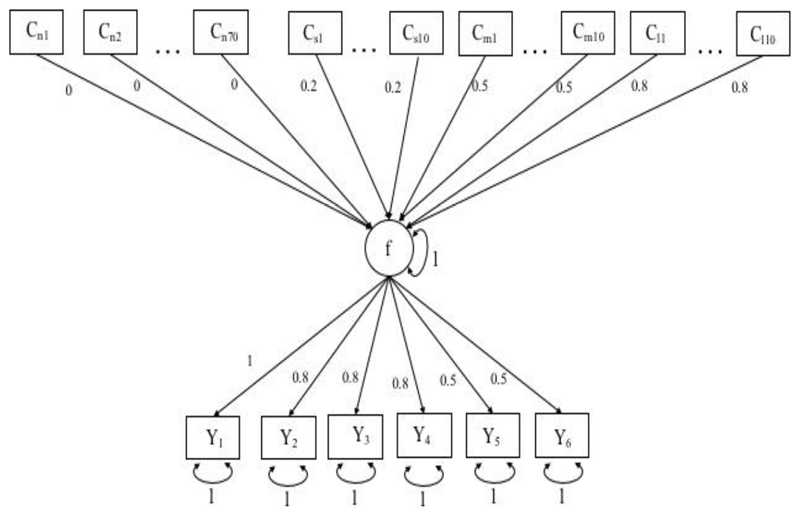
To evaluate the effectiveness of the RegSEM Lasso, we designed simulation conditions that researchers may commonly face when evaluating a large number of predictors (e.g., a property such as cortical thickness measured across many brain regions). We vary our simulations across two dimensions: sample size and predictor collinearity. The template model with each simulated parameter is depicted in Figure 3 below. In this, there are six indicators (Y1-Y6) of the latent variable, f. These factor loadings differ in their simulated population values (see Figure 3). As predictors of f, there are 70 uninformative (“noise”) variables (C_n1-C_n70), with simulated population coefficients of zero. Additionally, there are three sets of 10 predictors each of differing effect sizes: small (0.20, C_s1-C_s10), medium (0.50; C_m1-C_m10), and large (0.80; C_l1-C_l10). Taken together, this makes a dataset of 100 potential predictors of f, each treated as fixed effects. In fitting this model, the latent variable variance was fixed to one for identification purposes, allowing each factor loading to be freely estimated (we do not estimate a mean structure).

Figure 3.

Template simulation model. The model is a MIMIC model including a single latent factor “f”, six indicators (Y1 to Y6) with factor loadings between .5 and 1 and unique error variances, as well as hundred potential predictors. The predictors are either uninformative (Cn1 to Cn70), have a small effect (Cs1 to Cs10), a moderate effect (Cm1 to Cm10) or a strong effect (Cl1 to Cl10).

After creating simulated data according to the model in Figure 3, we then tested a model that included 112 free parameters, including one hundred latent regression coefficients, 6 factor loadings, and 6 residual variances. Although rules of thumb are inherently limited, common guidelines would suggest a ratio of 10:1 for sample size, suggesting a minimum N of 1,200 (e.g. Kline, 2015) to obtain stable estimates. Given that many researchers may wish to test models of this size, but may not have the requisite sample size, we aimed to test a variety of sample sizes to examine when the performance of MLE degrades. and when the use of regularization is beneficial. As a result, we tested sample sizes² of 150, 250, 350, 500, 800, and 2000.

Finally, in most psychological studies that examine the influence of a variety of predictors, it is common that these predictors have correlations amongst themselves. This complicates the interpretation of the results – for instance, it becomes challenging to determine the relative contribution of individual predictors (Grömping, 2009). Moreover, high degrees of collinearity can result in problematic estimation. As a result, we also included predictor collinearity as a simulation condition. To investigate the effect of predictor collinearity, we simulated data that included correlations of 0, .20, 0.50, 0.80, and 0.95 among all predictors. With increasing correlation, we expected increasing amounts of bias in both MLE and regularized estimation. Because Lasso regularization is problematic with high degrees of collinearity, we also included the Elastic Net estimator. Finally, we examine the prevalence of Type I (wrongly including a noise predictor) and Type II (wrongly excluding a true predictor) error rates across a range of sample sizes and effect sizes.

To test each form of estimation, we used two different packages in the R statistical environment (R Core Team, 2018). For MLE, we used the lavaan package (version 0.5-23.1097; Rosseel, 2012). For RegSEM, we used the regsem package (version 1.0.6; Jacobucci, Grimm, Brandmaier, & Serang, 2017). Both Lasso and Elastic Net regularization are implemented in regsem, along with a host of additional penalties (Jacobucci, 2017). We vary the penalty term lambda (see equation 4 above) across 30 values, ranging from 0 to 0.29 in equal increments. In initial pre-runs, higher penalty values were used but always resulted in worse fit at the higher ranges. To choose a final model among the 30 models run, we used the Bayesian information criteria (Schwarz, 1978). Across all of the simulation conditions, each cell was replicated 200 times. Our simulation code and other material can be found at https://osf.io/z2dtq/.

Results

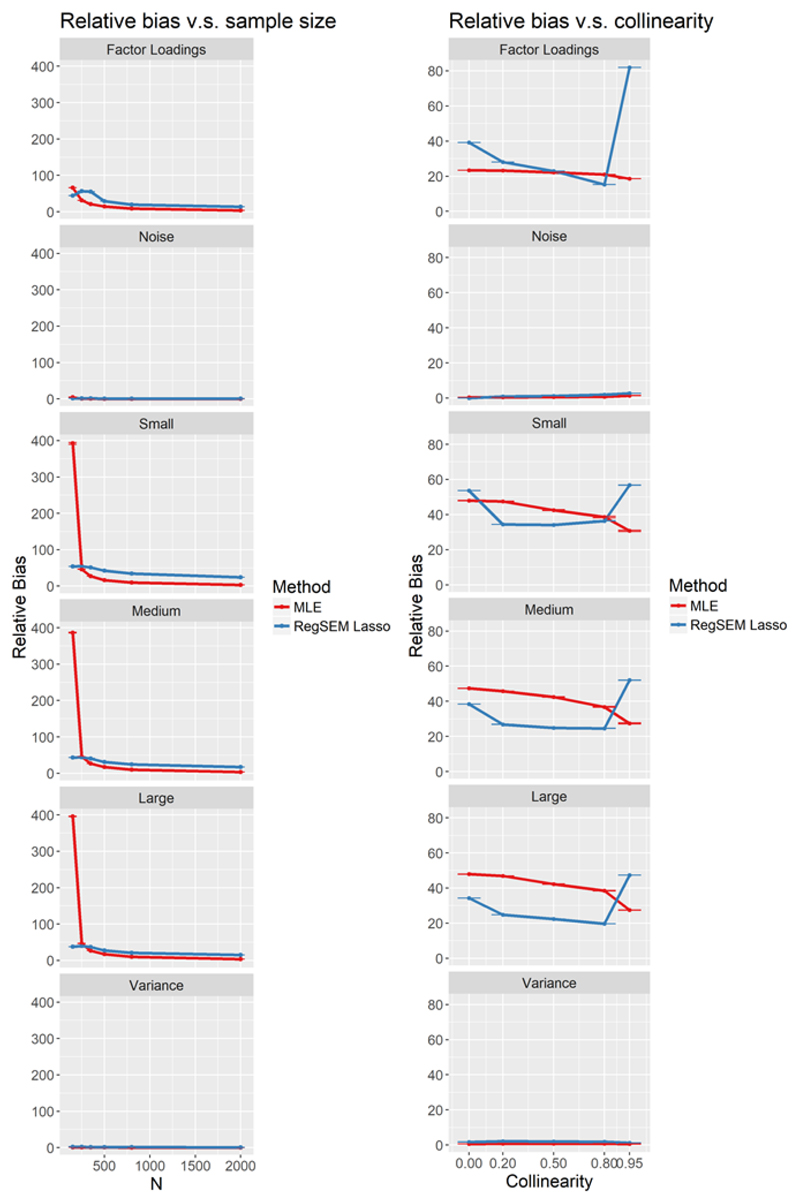
Instead of giving a detailed analysis of each figure, we instead give a high level overview of simulation results. We compare the performance of RegSEM Lasso to MLE across three performance metrics: Root Mean Square Error (RMSE; averaged across each set of parameters), relative bias (RB; averaged across each set after taking the absolute value of each parameter) and and error type (type I and type II respectively). For each performance metric we vary sample sizes (left panels) and collinearity (right panels). We do not present the results for RegSEM Elastic Net estimation, as the results were almost identical to those from RegSEM Lasso.

Parameter Estimates

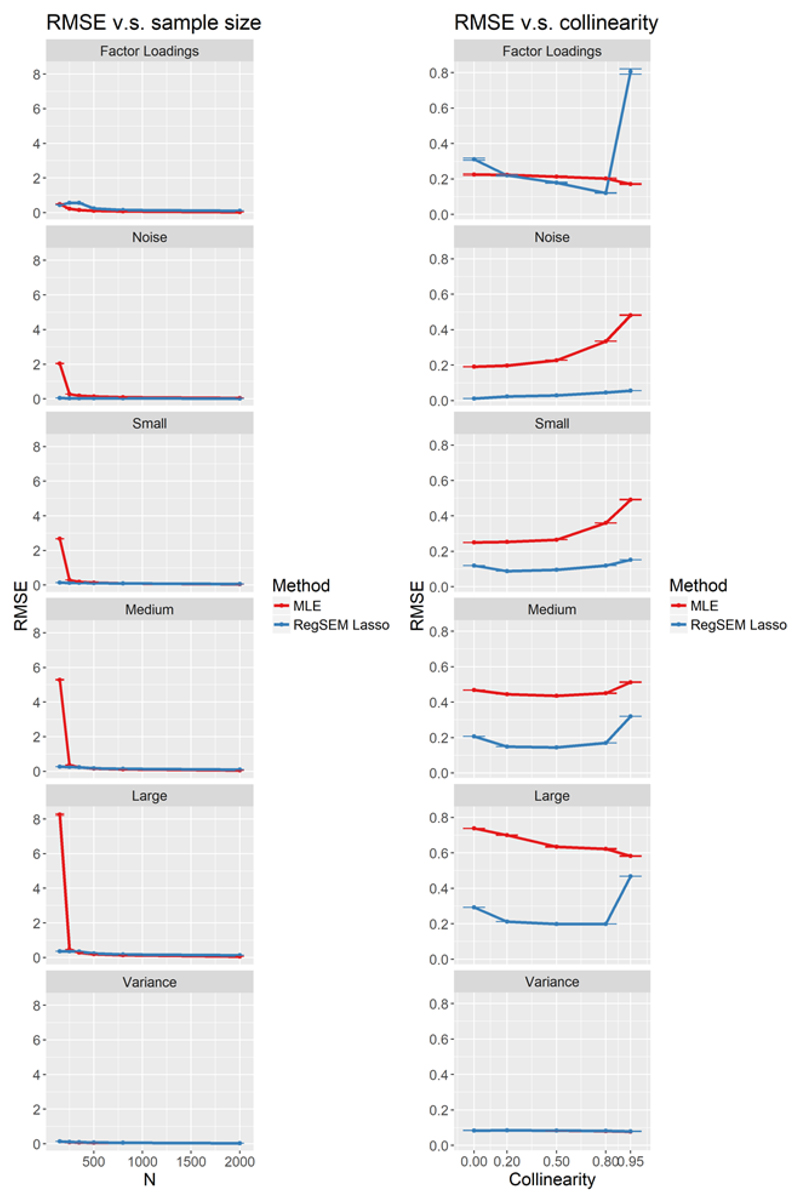
First we examine the precision of parameter recovery quantified as RMSE and relative bias (RB). At higher sample sizes, MLE performed well in comparison to Lasso with regard to RMSE, and even more so for RB. This performance distinction with RegSEM Lasso between both metrics is as expected, because as we discussed earlier, the Lasso imparts bias to reduce variance. RMSE measures both bias and variance, while RB only measures bias, thus the increase in bias is somewhat offset by a decrease in variance. At smaller sample sizes, the Lasso performed better than MLE, particularly at a sample size of 150. With only 150 observations, MLE was highly unstable in its estimation of parameters, meaning parameter estimates were drastically larger than their simulated values.

In using RMSE, there was remarkably similar performance across both MLE and Lasso, with the exception of sample sizes of 150 and 250. Using the RMSE, the Lasso produced better results in most conditions, whereas the results with RB were more mixed. When the amount of correlation among all predictors was extremely high (0.95), the Lasso produced a large amount of RMSE in the factor loadings. As displayed in the top right pane of Figure 4, this large increase in RMSE mostly likely is what also produced higher RMSE values for the Lasso and sample size for the factor loadings (top left pane). This can most likely be explained by covariance expectations, and how correlations among predictors create a more complicated web of relationships (see Appendix A for further detail). Fortunately, collinearity of predictors in the range of .95 is unlikely to be observed in real datasets.

Figure 4.

Root mean square error across a range of sample size (left panels) and predictor collinearities (right panels) for MLE (red) and RegSEM lasso (blue).). The individual panels refer to the factor loadings, the uniformative predictors(noise), to the informative predictors of different effect sizes (small, medium, strong), and the residual error variances (variances). Error bars represent monte carlo standard errors.

The Lasso was favored with respect to RB for the sample size of 150, but MLE was favored with larger samples. The same effect that occurred for the Lasso and RMSE with extreme degrees of collinearity also occurred for RB. This secondary effects were much less present using MLE. Additionally, in comparison to RMSE, collinearity resulted in a U-like effect on the Lasso for RB for the regression coefficients. Both small (0) and extreme (0.95) correlations among predictors resulted in the highest RB, whereas this same relationship did not hold for MLE. Together, our simulations show that regularized SEM outperforms traditional MLE in terms of parameter estimation in cases where sample sizes are small and the number of predictors is large.

Type I and Type II Errors

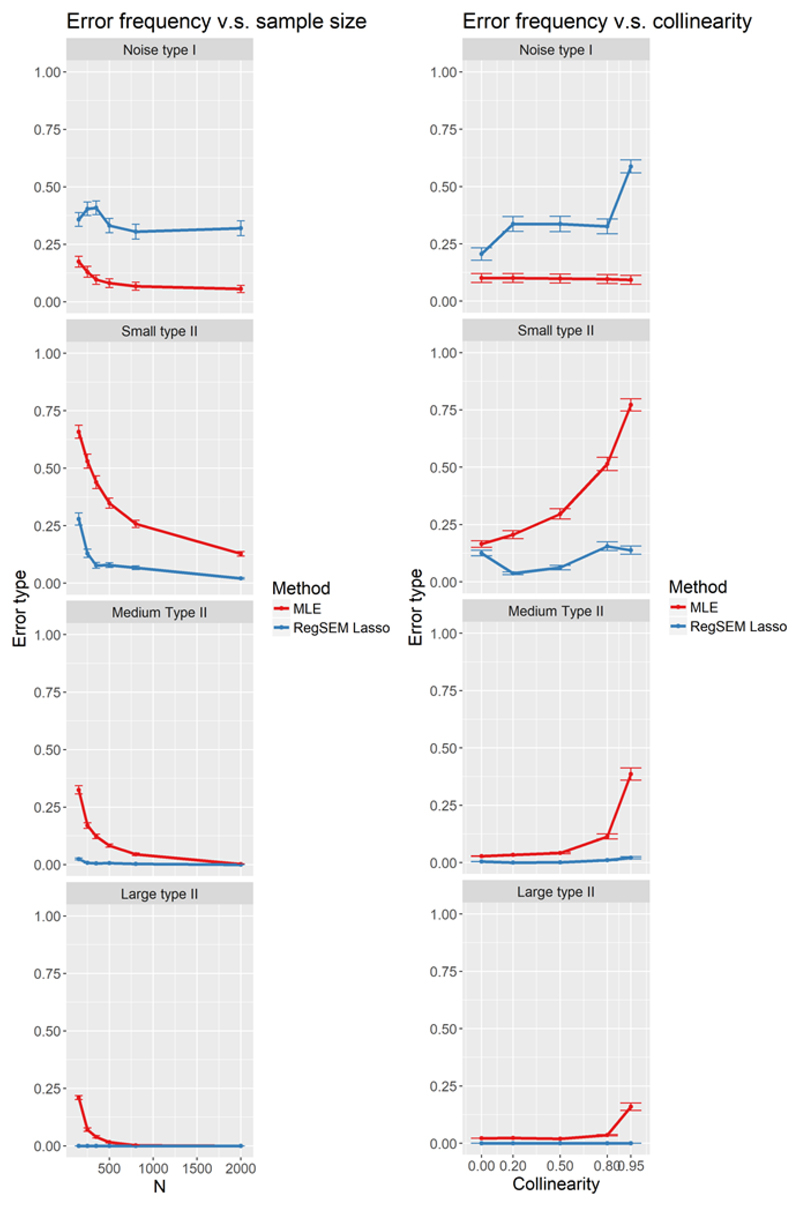
An alpha criterion of 0.05 was used to determine parameter significance in the MLE models (see Figure 6). First looking at the propensity of a Type I error with the noise parameters (if a noise variable had a p-value < 0.05), sample size had a larger effect than did collinearity for MLE. For a sample size of 150, this means a 17% chance to incorrectly identify a noise variable as a significant parameter. For collinearity, although the Type I errors rates were higher than 0.05, this can mostly be attributed to the influence of the sample size conditions. More alarming is the low power, or high Type II error rates (p-value > 0.05) for the small and medium parameters in MLE. As collinearity increases, so does the Type II error rates for these parameters, while the inverse relationship holds for sample size. Even for the parameters simulated at a value of 0.8, larger than expected numbers of Type II errors were committed at small sample sizes and a large amount of collinearity. For the Lasso, almost opposite results occurred. Overall, the Lasso committed far more Type I errors with the noise variables (estimating noise variables as non-zero), but also had much lower Type II errors (i.e., it rarely omitted a truly predictive variable) across the small, medium and large variables in each condition.

Figure 6.

Type I and Type II erorrs for predictors of small (top) medium (middle) and large (bottom) size, tested across a range of sample size (left panels) and predictor collinearities (right panels) for MLE (red) and RegSEM lasso (blue). Error bars represent monte carlo standard errors.

Summary

Across our simulations, MLE performed better at larger sample sizes, the Lasso better at smaller numbers of observations. Across both metrics, MLE had less relative bias (as expected), while in some cases the Lasso improved upon MLE with respect to the RMSE. These results are in line with previous work such as Serang, Jacobucci, Brimhall, and Grimm (2017), who found a similar tradeoff between regularization and other forms of estimation in the context of mediation models. Parameter estimate accuracy had a less stark contrast in the performance between methods. The optimal method for a given research context depends on the relative importance of decreasing parameter bias or parameter variance. Although MLE may produce more accurate results within your sample, this model may not generalize as well as a model produced using regularization. This contrast goes beyond the small selection of models discussed in this paper.

Study 2: White matter determinants visual short term memory

In cognitive neuroscience, where many features of brain structure and function may have complementary effects, the challenge is how to best reconcile the dimensionality constraints for covariance based methodologies such as SEM, with the richness of the imaging metrics (which may include hundreds of measures per individual). Here, we describe an illustrative example using regularized SEM on a large, population-derived cohort of healthy aging individuals (Cam-CAN, Shafto et al., 2014), modelling visual short term memory as a function of white matter microstructure.

Sample

For this empirical illustration we use data from the Cambridge Study of Cognition, Aging and Neuroscience (Cam-CAN, www.cam-can.org). The sample consists of 627 participants, 320 female, between the ages of 18 and 88 (M =54.18, SD=18.42) who participated in a large battery of cognitive tests, demographic and lifestyle measurements, and MRI scans (for more detail on the cohort and sampling methodology see Taylor et al., 2017). Here we focus on a specific cognitive task (the visual short term memory task) and a common index of white matter microstructure (Fractional Anisotropy, FA) for participants with complete data. Subsets of this data (but not this cognitive task) have previously been reported (e.g. Henson et al., 2016; Kievit et al., 2014, 2016).

Visual Short Term Memory

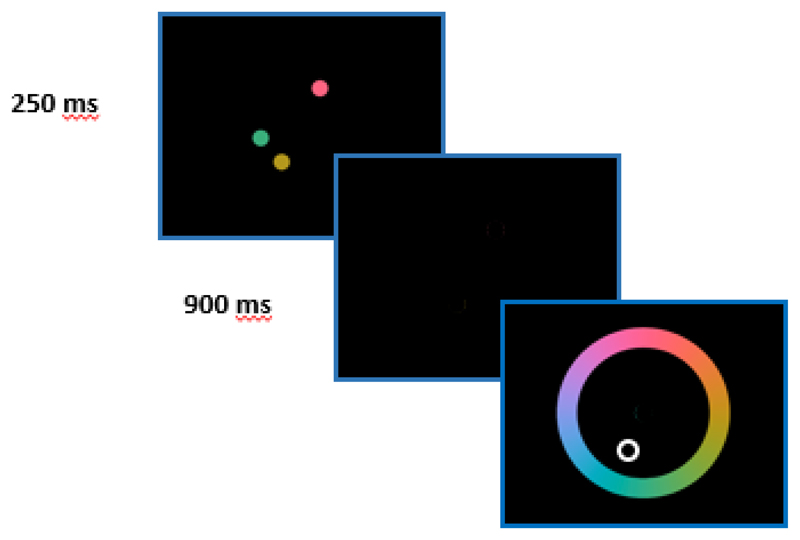
This particular visual short term memory task was developed to quantify capacity and precision of short term visual memory. The task consists of three phases: an encoding phase, during which participants view between one and four coloured circles, followed by a brief blank screen (900 milliseconds) and a cue in the same spatial location as one of the (up to) four circles (see Figure 7). Participants are asked to use a colour wheel to pick the colour of the cued circle, as well as rate their confidence in their judgment. Participants performed a total of 224 trials across two blocks, with position, set size, and cues counterbalanced across blocks. We here focus only on set size (defined as the visual capacity of an individual estimated for each set size) for set sizes 2-4 (to avoid the ceiling effects associated with the simplest version). Each participant had three scores capturing their mean performance across the three set sizes, with each score ranging between 0 and the maximum number of circles per set size (i.e. 2-4).

Figure 7.

Visual short term memory task. Participants view between 1 and 4 targets for 250 milliseconds, followed by a 900 ms blank screen. Finally they receive a cue for one of the previous targets, and are asked to respond, using a color wheel, which hue most closely matched that of the target.

White matter

For the neural indicators we use a common metric of white matter organization called Fractional Anisotropy. This metric quantifies the dispersion of water molecules and the extent to which this dispersion is constrained by the organization of white matter structures. FA is a complex and indirect measure with various limitations, and the relationship between FA and white-matter health is not yet fully understood (Jones, Knösche, & Turner, 2013; Bender, Prindle, Brandmaier, & Raz, 2016). Nonetheless, FA is widely used as it has been shown to be associated with individual differences in a range of cognitive domains, especially in old age (Madden et al., 2009). We here focus on mean FA for each tract using the ICBM-DTI-81 atlas (Mori et al., 2008) which parcellates the human white matter skeleton in 48 tracts. Although we have previously focused on white matter atlases of lower dimensionality (e.g. (Kievit et al., 2016 and Mooij, Henson, Waldorp, Cam-CAN, & Kievit, 2018), we here intentionally use a more high-dimensional white matter tract atlas to illustrate the benefit of regularization. For more details regarding the pipeline, see Kievit et al (2016).

MIMIC-model

To examine the neural determinants of visual short term memory we fit a Multiple Indicator, Multiple Causes model (Joreskog & Goldberger, 1975). This model captures the hypothesis that a latent variable measured by multiple indicators is in turn affected by multiple causes (cf. Kievit et al., 2012 for a comparison of the MIMIC model to competing representations). First, we specify a measurement model such that a latent variable is measured by the memory capacity across three subtests varying in set size (2, 3 and 4, see above for more details). Next, we simultaneously regress this latent variable on all 48 white matter tracts. This model tests the joint prediction of the latent variable by all 48 tracts which allows one to quantify if one or more white matter tracts help predict individual differences in visual short term memory.

Model estimation and results

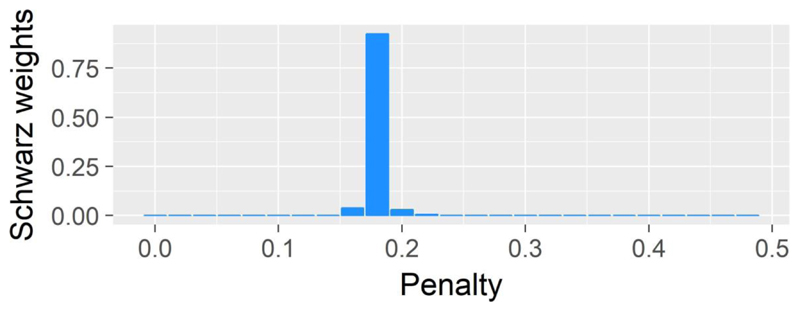
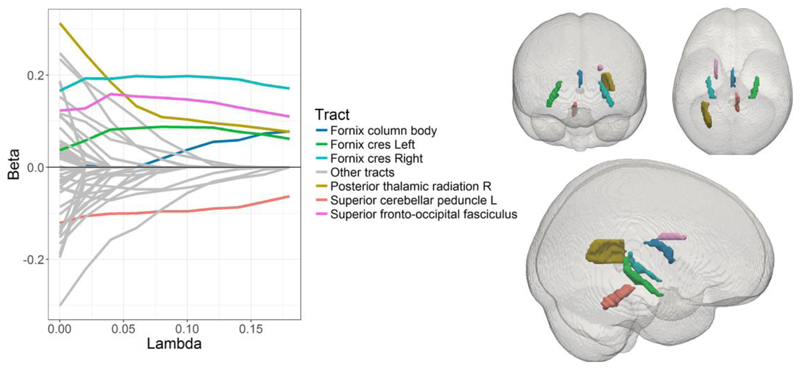
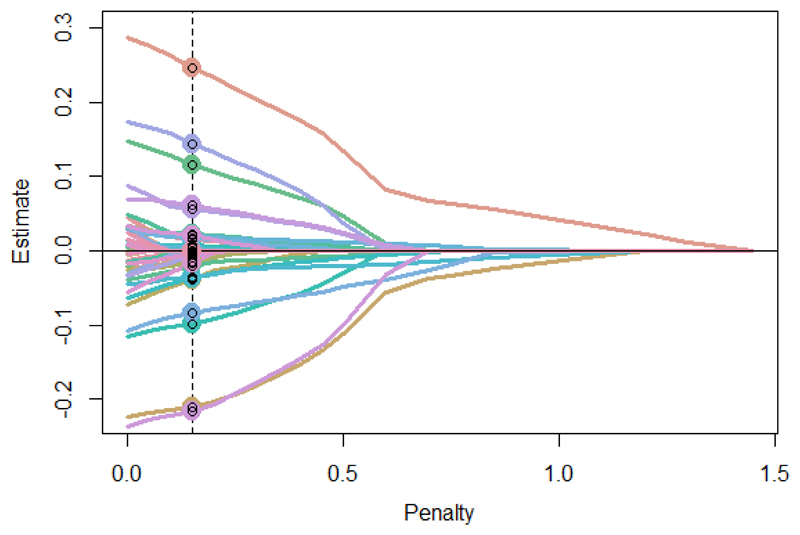
We estimate the regularized model across a range of lambda values, using the Bayesian Information Criterion (BIC; also Schwarz Criterion; see Jacobucci, Grimm, & McArdle for further detail on alternative strategies for selecting a final model) to compare model fit across each iteration. The BIC balances the extent to which the increased parsimony of regularizing parameters to 0 simplifies the model with the concurrent decrease in explanatory power of the reduced model. As we have a strong a priori hypothesis about the measurement model we only regularize the structural parameters (i.e. the joint prediction of the latent variable by 48 tracts), not the factor loadings or residual variances. As can be seen in Figure 8, the best solution by BIC is obtained with a lambda value of 0.18, which yields an acceptable RMSEA of 0.0321. Figure 9 shows the beta estimates and model BIC across a range of lambdas, as well as the six tracts that are non-zero in the final model.

Figure 8.

Schwarz Weights (cf. Wagenmakers & Farrell, 2004) across a range of penalty values (lambda), suggesting a penalty of .18 is optimal._Higher weights correspond lower BIC values, meaning a better fitting model.

Figure 9.

In the final model six non-zero tracts for this penalty are shown as individual colors (top left and top right panels) whereas the tracts regularized to 0 are shown in grey.

Results

As can be seen in Figure 9, six tracts remain non-zero in the regularized MIMIC model. Strikingly, three of these are subdivisions of the fornix (the column and body, as well as the cres), all showing positive effects (i.e. greater white matter microstructure is associated with better visual short term memory performance). The fornix, a tract connecting the hippocampus to other brain regions, has long been associated with various aspects of memory, usually autiobiographic (e.g. Hodgetts et ell., 2016) or, in the same Cam-CAN cohort, subdomains such as recollection, familiarity and priming (Henson et al., 2016). Notably, there are even some phase I trials suggesting deep brain stimulation to the fornix may alleviate memory complaints in early Alzheimer’s sufferers (Laxton et al., 2010). The posterior thalamic radiations (see Figure 9 top right) have been posited as crucial in focusing and allocation attention in demanding tasks (Menegaux et al., 2017). Evidence in infants suggests distinctive association between greater white matter organization in the posterior thalamic radiations and better performance on the visual short term memory task (Menegaux et al., 2017). Finally, we observe a positive association between the superior fronto-occipital fasciculus, previously associated with greater spatial working memory in children (Vestergaard et al., 2011).

Although the above five tracts align well with previous literature, we also observe a single (surprising) negative effect – Greater white matter integrity of the Superior cerebellar peduncle was associated with poorer VSTM performance. However, closer inspection of this tract suggests that this pattern is likely an artefact of image registration as (unlike other tracts) the integrity of this tract (bilaterally) increases with age. A likely explanation is that the relatively deep location of this tract within the brain makes it vulnerable to registration challenges such as partial volume effects (Alexander, Hasan, Lazar, Tsuruda, & Parker, 2001). For these reasons we suggest this ‘negative’ pattern is more likely to represent an imaging artefact than a true association.

It should be noted that the regularized model solution does not imply that all other tracts are uncorrelated to VSTM. In cases of collinear predictors a regularized solution is more likely to yield a predictor most ‘representative’ of a broader set of correlated predictors (i.e. a single tract captures most or all of the predictive power across a network of tracts). In this case, regularizing “groups” of predictors with the group lasso (Friedman, Hastie, & Tibshirani, 2010) may be more appropriate, however, this has not been generalized to SEM at this time. To summarize, a regularized SEM-MIMIC is able to model the relation between cognitive performance and imaging metrics with a high dimensional set of predictors into a relatively parsimonious representation of key tracts previously implicated in visual short term memory performance. This demonstrates the viability of this methodology in cognitive neuroscience in general and aging and developmental cohorts in particular.

Study 3: Modeling the determinants of depression, anxiety and stress

Sample

Previous work suggests many distinct predictors of individual differences in stress, anxiety and depression (e.g. Sümer, Poyrazli, & Grahame, 2008), but it is often unclear to what extent these are separable or collinear (non-unique) determinants of mental health. For our second empirical example we examine this question using a large (N= 27,835) publicly available dataset of the Depression, Anxiety Stress (DASS) scale (Lovibond & Lovibond, 1995). This dataset was collected as an online sample and is freely available at https://openpsychometrics.org/_rawdata/. The 42 item DASS scale captures latent variables of depression, anxiety and stress (each with 14 indicators) as well as a set of personality and demographic covariates, which will be subject to regularization. These covariates include the Ten Item Personality inventory (Gosling, Rentfrow, & Swann, 2003), each rated on a 7 point likert scale (Disagree strongly to Agree Strongly). Other covariates included are education (ranging from 1=’less than high school’ to 4 ‘graduate degree), gender (1=Male, 2=Female, Age (in years), handedness (1=Right, 2=Left), voter record (1=’I have voted in the last year’) and family size (‘Including you, how many children did your mother have’). These covariates are included for illustrative, rather than conceptual, reasons.

Results

First, we fit a three factor measurement model to the full DASS scale. This model fit the data well (X²(816) = 64,490.79, p < .001; RMSEA = .053 [.053 - .053]; CFI = .897; SRMR = .040), and all factor loadings were moderate to strong (range=0.50-0.84, Mean=.7). Despite considerable covariance (correlations all >.7) among the latent variables, a three factor model fit considerably better than a competing unidimensional account (where all items are taken to measure a single latent variable; ΔX²= 29,414, (Δdf=3), p < .001). Next, we fit a MIMIC model where the three latent factors were simultaneously regressed on the 16 predictors. Results here are based on a random subsample (N=1000) of the full cohort. Model fit was good (X²(1,440) = 4,348.61, p < .001; RMSEA = .045 [.044 - .046]; CFI = .884; SRMR = .038), and the joint covariates predicted a large amount of variance (stress; 52.3%, Anxiety, 41.9%, Depression, 40.7%). With MLE, 4 predictors are nominally significant for stress, 7 for anxiety and 6 for depression (in the N=1,000 subsample).

Next, we refit the model using Lasso RegSEM. As can be seen in the Figure 10, the optimal BIC solution was observed with a lambda penalty of 0.15. Of the total 48 structural parameters, this penalty regularized twenty-seven paths to zero, yielding a more parsimonious model representation. Table 2 shows the fully standardized parameter estimates for the ML solution as well as the regularized model. Consistent across all three factor, the personality items 4 (‘easily upset, anxious’) and 9 (Calm, emotionally stable) had strong associations (r=~3 with the three mental health outcomes). However, both MLE and Lasso estimates demonstrate that a considerable number of other predictors contribute unique variance in explaining individual differences in mental health, including education and the ‘reserved, quiet’ personality dimensions.

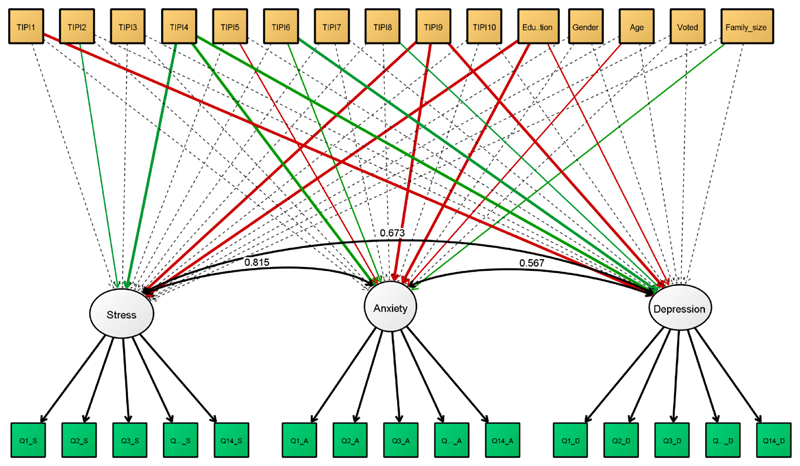
Figure 10.

MIMIC model of stress, anxiety and depression. Non-significant predictors are shown as dashed lines, with significant paths (α<0.05) shown as positive/negative (green/red) and strong/weak (thick vs thin lines, reflecting Z-scores>3 and <3). Variances were omitted from this figure.

Table 2. Fully standardized regression parameters from both the ML and Lasso models.

Regression Parameter	ML Standardized Estimate	Wald Test Z Value	Lasso Estimate
TIPI1 -> stresslv	-0.018	-0.55	-0.003
TIPI2 -> stresslv	0.062	2.14	0.029
TIPI3 -> stresslv	-0.043	-1.54	-0.007
TIPI4 -> stresslv	0.394	10.65	0.134
TIPI5 -> stresslv	-0.044	-1.42	-0.002
TIPI6 -> stresslv	0.041	1.37	0
TIPI7 -> stresslv	-0.032	-1.28	0
TIPI8 -> stresslv	-0.009	-0.31	0
TIPI9 -> stresslv	-0.307	-8.3	-0.103
TIPI10 -> stresslv	0.004	0.14	0
education -> stresslv	-0.099	-3.3	0
gender -> stresslv	0.047	1.88	0
age -> stresslv	-0.035	-1.52	-0.012
hand -> stresslv	-0.002	-0.08	0
voted -> stresslv	0.005	0.19	0
familysize -> stresslv	0.012	0.46	0
TIPI1 -> anxietylv	-0.007	-0.2	0
TIPI2 -> anxietylv	0.029	0.97	0
TIPI3 -> anxietylv	-0.041	-1.24	0
TIPI4 -> anxietylv	0.293	7.51	0.069
TIPI5 -> anxietylv	-0.078	-2.29	-0.016
TIPI6 -> anxietylv	0.098	3.06	0.003
TIPI7 -> anxietylv	-0.027	-0.87	0
TIPI8 -> anxietylv	0.013	0.42	0.014
TIPI9 -> anxietylv	-0.228	-5.7	-0.05
TIPI10 -> anxietylv	0.026	0.84	0
education -> anxietylv	-0.125	-3.68	0
gender -> anxietylv	0.014	0.5	0.017
age -> anxietylv	-0.089	-2.02	-0.013
hand -> anxietylv	0.015	0.54	0
voted -> anxietylv	0.057	1.97	0
familysize -> anxietylv	0.064	2.21	-0.006
TIPI1 -> depressionlv	-0.14	-4.12	-0.04
TIPI2 -> depressionlv	0.042	1.5	0
TIPI3 -> depressionlv	-0.041	-1.32	0
TIPI4 -> depressionlv	0.224	6.22	0.046
TIPI5 -> depressionlv	-0.044	-1.33	0
TIPI6 -> depressionlv	0.113	3.53	0.027
TIPI7 -> depressionlv	0.012	0.43	0
TIPI8 -> depressionlv	0.089	2.87	0.043
TIPI9 -> depressionlv	-0.306	-8.5	-0.118
TIPI10 -> depressionlv	0.042	1.45	0
education -> depressionlv	-0.071	-2.37	0
gender -> depressionlv	-0.022	-0.85	0
age -> depressionlv	0.01	0.43	-0.009
hand -> depressionlv	-0.005	-0.17	0
voted -> depressionlv	0.02	0.74	0
familysize -> depressionlv	0.031	1	0

Of note in Table 2 is that the largest Wald test Z values do not consistently correspond to what is selected as non-zero in the Lasso model. One thing to keep in mind when interpreting the Lasso parameter estimates is that these are biased towards zero due to the shrinkage (Tibshirani, 1996). One solution to this is to refit the model without any penalty in a second stage using only the chosen subset. This procedure is referred to as the relaxed lasso (Meinshausen, 2007) and has been shown to perform favorably when compared to best subset selection, forward stepwise selection, and the lasso without the second stage (Hastie, Tibshirani, & Tibshirani, 2017; Serang,Jacobucci, Brimhall, & Grimm, 2017). Because we did not follow this two-stage approach, it is recommended to only interpret the regularized coefficients as zero or non-zero.

Discussion

Here we propose regularized SEM as a powerful and underutilized method for researchers who want to examine a (relatively) large number of predictors, or have a relatively modest sample size in SEMs of moderate complexity. We described regularization as applied to both regression and structural equation modeling, and evaluated its use in high dimensional MIMIC models. We show how Lasso penalties incurred less error in conditions with small sample sizes, and demonstrated higher power in detecting regression paths of varying magnitude. Across these results we identified how sample size and the correlation among regressors influences the accuracy and inference of parameter estimates in an extremely complex model. This was applied to modeling visual short term memory as a function of white matter microstructure in a large existing dataset. Starting with a complex model of 48 distinct white matter tracts, the regularized model yielded six distinct tracts with non-zero parameter estimates as determinants of visual short term memory. Finally, our last example identified a broad set of variables that explain individual differences in stress, anxiety and depression.

Our simulation study showed that regularized SEM may be a viable option for researchers looking to identify a relatively low-dimensional set of predictors in fields with broad sets of candidate variables, such as cognitive neuroscience and behavior genetics. Notably, this technique goes beyond traditional mass univariate methods of multiple comparison corrections in neuroimaging such as false discovery rate or Gaussian random field theory (for an accessible introduction, see Brett et al., 2003), which are generally still implemented to correct (mass) univariate tests, rather than joint simultaneous prediction across voxels/regions of interest. It may be possible to combine the above approach with joint methods such as principal component regression to estimate the joint prediction of multiple components across many voxels even in cases with modest sample sizes (e.g., Wager et al., 2011).

Limitations and challenges

Although we have illustrated several benefits of regularization in regression and SEM for small sample sizes, we did not include any conditions with N < 100. This was mostly due to the complexity of our model, as we were unable to achieve stable estimates at a sample size of 120 or below. In regularized regression it is possible to test models with p > n, however, to our knowledge, this has not been done using traditional SEM estimation methods such as MLE. A possible solution is the use of Bayesian SEM, where strongly informative priors or hierarchal models with sparsity inducing priors can achieve stable estimation even in such extreme cases (see Jacobucci & Grimm, in press). Given the use of Bayesian estimation in cases of small numbers of observations (McNeish, 2016), we expect to see more research in this realm in the future, as pairing Bayesian SEM and regularization has seen a wider array of application than with frequentist SEM (see Feng, Wu, & Song, 2017; Brandt, Cambria, & Kelava, 2018; Lu, Chow, & Loken, 2016). Other avenues for future work include the investigation of bias in the use of regularization in factor score regression approaches (Devlieger & Rosseel, 2017), which may help overcome the current n > p boundary. Additionally, by first creating factor scores, thus fixing the factor loadings, bias induced by high degrees of collinearity may be reduced.

Frequentist software for regularized SEM currently requires complete cases. As it is rare for psychological data to have no missingness, this currently represents a considerable weakness of regularized SEM. One strategy for modeling data with missing values is the use of multiple imputation. The main issue with multiple imputation and regularization is combining the results. In traditional multiple imputation for SEM, the parameter estimates can be aggregated across the 10-20 datasets by averaging the parameter estimates and correcting the standard errors for the lack of randomness in the process. However, regularization is most often used to perform variable selection, thus necessitating a way to aggregate a set of 0-1 decisions across imputed datasets. Although some research has addressed this in regression (Liu, Wang, Feng, & Wall, 2016), this is not been generalized to SEM.

Without p-values or confidence intervals accompanying each parameter estimate, researchers may feel less certain regarding inference when using regularization. Although Lockhart, Taylor, Tibshirani, and Tibshirani (2014) have derived sampling distributions to calculate p-values that take into account the adaptive nature of the Lasso regression model, this has not been done with Lasso in SEM. Because of this, inference can be more challenging in regularized SEM models, particularly given the inherent bias in estimation. One method proposed for overcoming this is the relaxed Lasso (Meinshausen, 2007), which has been shown to produce unbiased parameter estimates with the Lasso applied to mediation models (Serang, Jacobucci, Brimhall, & Grimm, 2017). Despite this, it may be difficult to change one’s mindset in characterizing non-zero paths as important. For this, we recommend a conceptualization that relates to an alternative sample. Although we may incur bias through the use of regularization, our more important aim is that of generalization, which is achieved by reducing variance and preferring models of a complexity that is afforded by the observed data. This particularly holds in exploratory studies, where we are less concerned with within sample inference, and care more about using our model to inform future research.

In our simulation we found a tradeoff between MLE and RegSEM Lasso with respect to Type I and Type II errors – the RegSEM Lasso keeps more variables in the model (more Type I errors and less Type II), where MLE is more restrictive with respect to which variables are thought to be significant (Less Type I and more Type II). Our perspective is that in exploratory studies, we generally should prefer a liberal stance, that is, more emphasis should be given to the inclusion of potentially important variables, and less concern to possibly including variables that do not have either predictive or inferential value. In an ideal setting, researchers would apply regularized SEM to data from a pilot or initial study in the hopes of being maximally efficient in what variables are included in a future, possibly larger study. Our simulation study supports the idea that applying MLE when the sample is small and the number of variables is large will result in the exclusion of potentially relevant variables. Note however, that our conclusions rely not only on the choice of regularization but also on our specific heuristic for choosing the penalty. If researchers can afford to be more inclusive (i.e. can tolerate more Type I errors) or more exclusive (can tolerate more Type II errors) in variable selection, choosing different penalties may align better with their goals (see also Lakens et al., 2018).

Related approaches

Regularized SEM is only one of the new methods developed for structural equation modeling in larger datasets. Particularly in the area of variable selection, Structural Equation Model Trees (SEM trees; Brandmaier, von Oertzen, McArdle, & Lindenberger, 2013) and Forests (Brandmaier, Prindle, McArdle, & Lindenberger, 2016) are one alternative method. SEM trees directly use the observed covariates to partition observations, and in the process, only a subset of covariates are used to create a tree model, allowing researchers to uncover non-linearities and interactions in SEM. Additional methods include the use of heuristic search algorithms (e.g. Marcoulides & Ing, 2012), various methods for identifying group differences (Frick, Strobl, & Zeileis, 2015; Kim & von Oertzen, 2017; Tutz & Schauberger, 2015), and the use of graphical models for identifying latent variables (e.g Epskamp, Rhemtulla, & Borsboom, 2016). With increasing amounts of data sharing, facilitated by various new tools for data storage and sharing such as the Open Science Framework (https://osf.io/) and https://openfmri.org/ we can envision the utility of testing models much larger than our template simulation model. One of the biggest challenges is current software implementation. In this regard we expect Bayesian estimation to be particularly fruitful, especially in the creation of new sampling methods such as in the Stan software package (Carpenter et al., 2016). Easier to use interfaces for specifying models (see Merkle & Rosseel, 2015) are sure to facilitate wider use among psychological researchers. As discussed earlier, regularization can be accomplished through both frequentist and Bayesian estimation (see Jacobucci & Grimm, in press), with varying strengths and weakness to each approach.

Summary

We encourage researchers to think of regularization as an approach to allow the incorporation of confirmatory and exploratory modeling. Researchers have more flexibility to make both their uncertainty and knowledge concrete. This is particularly suitable if researchers hope to use a principled approach to go beyond the limitations of their theory to identify potentially fruitful avenues for future study. In both our simulation and empirical examples, we did an exploratory search for important predictors in relation to a confirmatory latent variable model. This is only one example in the fusion of these types of modeling and we look forward to see new areas for application. It is our hope that our exposition sheds light on a new family of statistical methods that have a high amount of utility for use in psychological datasets.

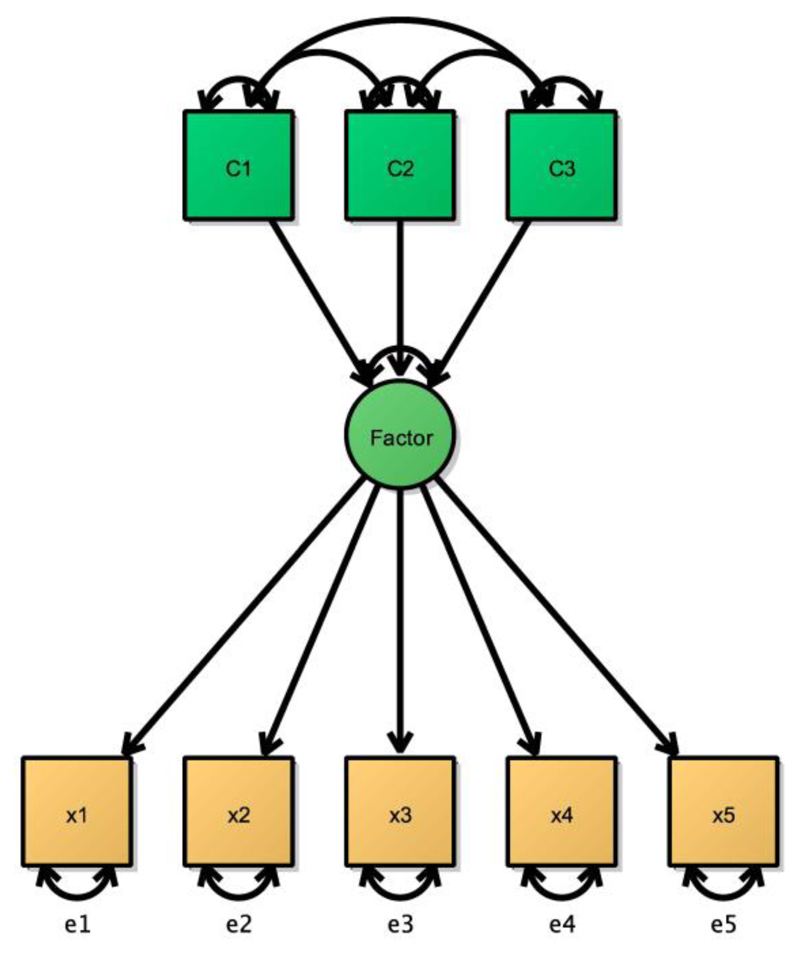
Figure 2.

Simple MIMIC model (multiple indicators X, multiple causes C).

Figure 5.

Relative bias across a range of sample size (left panels) and predictors collinearities (right panels) for MLE (red) and RegSEM lasso (blue). Error bars represent monte carlo standard errors.

Figure 11.

Parameter trajectory plot from the DASS data. The lowest BIC was at a penalty of 0.15.