Figure 1.

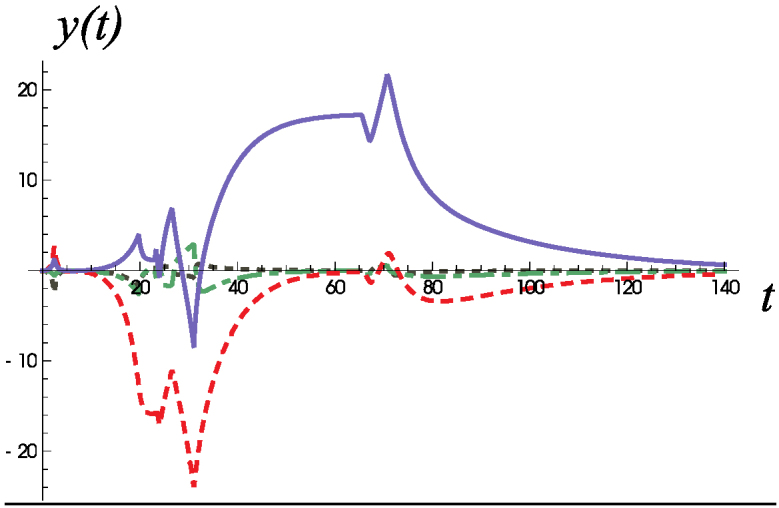
An example of stabilizing a four-dimensional subspace in a 40-dimensional space. Time dependencies of the variables y1…4, that determine the subspace for yi = 0 are shown. The first variable y1 (the blue solid line) corresponds to the first generation of the variables x1…x10 having the strongest coupling. The second variable, y2, (the red dashed line) is coupled to the variables x11…x20 with weaker coupling constants, scaled by the factor q = 0.4 with respect to the first variable. The third and the fourth generations (the dash-dot and the dotted lines, green and black, respectively) have couplings scaled by the factors q² and q³, respectively. Note seven sequential discontinuities of the derivatives of the dependencies related to the sign changes at the most nimble variables xi, that first occur in the first generation, then in the second, etc. The changes in each of the generations manifest themselves in all dependencies via the matrix $\widehat{\alpha }$. The scales of y( t) and t are arbitrary.