Force-Velocity Relationship in the Countermovement Jump Exercise Assessed by Different Measurement Methods

Abstract

This study aimed to compare force, velocity, and power output collected under different loads, as well as the force-velocity (F-V) relationship between three measurement methods. Thirteen male judokas were tested under four loading conditions (20, 40, 60, and 80 kg) in the countermovement jump (CMJ) exercise, while mechanical output data were collected by three measurement methods: the Samozino's method (SAM), a force platform (FP), and a linear velocity transducer (LVT). The variables of the linear F-V relationship (maximum force [F0], maximum velocity [V0], F-V slope, and maximum power [P0]) were determined. The results revealed that (1) the LVT overestimated the mechanical output as compared to the SAM and FP methods, especially under light loading conditions, (2) the SAM provided the lowest magnitude for all mechanical output, (3) the F-V relationships were highly linear either for the SAM (r = 0.99), FP (r = 0.97), and LVT (r = 0.96) methods, (4) the F-V slope obtained by the LVT differed with respect to the other methods due to a larger V0 (5.28 ± 1.48 m·s-1) compared to the SAM (2.98 ± 0.64 m·s-1) and FP (3.06 ± 0.42 m·s-1), and (5) the methods were significantly correlated for F0 and P0, but not for V0 or F-V slope. These results only support the accuracy of the SAM and FP to determine the F-V relationship during the CMJ exercise. The very large correlations of the SAM and LVT methods with respect to the FP (presumed gold-standard) for the mean values of force, velocity and power support their concurrent validity for the assessment of mechanical output under individual loads.

Introduction

The assessment of muscle strength is of paramount importance in many fields of sport sciences and related disciplines (Jaric, 2002). Regarding the field of strength training and conditioning, strength testing protocols are considered important means for prescribing individualized resistance training programs as well as for evaluating the training-induced effects (Abernethy et al., 1995; Gołaś et al., 2016, 2017; Morin and Samozino, 2016). A testing procedure that has recently received a wide attention consists of the assessment of muscle function through the force-velocity (F-V) relationship (Jaric, 2015; Morin and Samozino, 2016). Briefly, the modelling of the force and velocity data collected under two or more loading conditions provides a line that allows the assessment of the selective capacities of the muscles to produce maximal levels of force (F0), velocity (V0), and power (P0) (Jaric, 2016; Samozino et al., 2012). Unlike the F-V testing procedure, it should be noted that standard testing procedures conducted under a single mechanical condition do not allow for distinguishing between different mechanical capacities of the muscles since their outcomes (i.e., force, velocity, and power) are inter-dependent (Jaric, 2015). In this regard, the F-V approach has been recommended over the standard test conducted under a single mechanical condition since its outcomes provide higher informational value (Garcia-Ramos et al., 2017a; Jiménez-Reyes et al., 2017a; Sreckovic et al., 2015).

The vertical jump is one of the tasks most commonly used to evaluate the function of lower-body muscles (Cuk et al., 2014; Jiménez-Reyes et al., 2014; Samozino et al., 2014). Different measurement methods have been utilised during the routine testing of the loaded vertical jump (e.g, force platforms [FP], linear velocity transducers [LVT], accelerometers, mobile applications, infrared platforms, jump mats, etc.) (Balsalobre-Fernandez et al., 2015; García-Ramos et al., 2016b; Giroux et al., 2014). The FP along with the LVT have been the two measurement methods most utilised to record the values of force, velocity, and power during loaded vertical jumps (Cormie et al., 2007b; García-Ramos et al., 2016b; Hori et al., 2007). However, the Samozino's method (SAM) is receiving increasing attention as a simple method for measuring the mean values of force, velocity and power during vertical jumps (Samozino et al., 2008). Samozino's equations rely on vertical jump height (together with the system mass and push-off distance) which can be accurately determined from the flight time recorded by affordable devices such as infrared platforms or mobile applications (Balsalobre-Fernandez et al., 2015; Jiménez-Reyes et al., 2017a). Therefore, it seems important to determine the possible differences between these measurement methods considering the magnitude of the mechanical output (i.e., force, velocity, and power) obtained under individual loading conditions, as well as their influence on the F-V relationship.

Giroux et al. (2014) conducted a comprehensive analysis on the validity of different measurement methods (FP, linear position transducer, accelerometer and infrared platforms) for measuring force, velocity and power output during the squat jump (SJ). When compared to the FP data, the linear position transducer and SAM methods proved to overestimate and underestimate the mechanical output, respectively. On the contrary, in the countermovement jump (CMJ) exercise, no significant differences between the FP and SAM methods were reported (Jimenez-Reyes et al., 2017b). A plausible explanation for these apparently contradictory findings (i.e., higher values for the FP than the SAM in the SJ, but not in the CMJ) could be the different measurement methods that were used to estimate the jump height needed for the application of the SAM. Namely, while Giroux et al. (2014) used an infrared platform, which is known to underestimate jump height (Glatthorn et al., 2011), Jimenez-Reyes et al. (2017b) used a FP which provided a more accurate estimation of vertical jump height. Therefore, it would be necessary to assess whether the SAM could also underestimate the mechanical output (i.e., force, velocity, and power) as compared with the FP method when the jump height is obtained from an infrared platform.

To address the existing gaps in the literature, we designed the present study to comprehensively examine the differences in the main outcomes typically assessed during the routine testing of loaded vertical jumps between different measurement methods (SAM, FP, and LVT). Specifically, we compared the three measurement methods (1) the values of force, velocity, and power collected under different loading conditions during the CMJ exercise, and (2) the F-V relationship and its variables depicting the maximal capacities of the muscles to produce force (F0), velocity (V0), and power (P0). We hypothesized that (1) the LVT and SAM methods would provide the highest and the lowest magnitude of mechanical output, respectively, and (2) the slope of the F-V relationship would differ when obtained by the LVT method as compared to the SAM and FP methods due to an overestimation of V0 by the LVT.

Methods

Participants

Thirteen male judokas, members of the national judo training centre of Valencia in Spain (age: 23.1 ± 3.2 years; body mass: 74.7 ± 7.3 kg; body height: 177.1 ± 7.0 cm; back squat one-repetition maximum (1 RM): 172.6 ± 47.5 kg) participated in this study. The study was carried out at the end of a special preparation mesocycle and participants were experienced with the loaded CMJ exercise. All the participants had been practicing judo for at least 10 years. Their technical levels ranged from the first to the third Dan black belt and all of them had a high competition level (all had been medallists in junior or senior National Championships in Spain, Georgia and Dominican Republic, five in junior or senior European Cups, five in Continental Opens, two in Junior Continental Championships, and one in World Junior Championships). They reported no chronic diseases or recent injuries that could compromise tested performance. Participants were instructed to avoid any strenuous exercise for the two days preceding the testing session. They were informed of the procedures to be utilised and signed a written informed consent form prior to investigation. The study protocol adhered to the tenets of the Declaration of Helsinki and was approved by the University of Granada Review Board.

Measures

Participants performed a 10 min standardised warm-up that included jogging, dynamic stretching, joint mobility exercises, unloaded CMJs, and one set of five repetitions performed against an external load of 20 kg (mass of the unloaded Smith machine barbell) during the CMJ exercise. The testing procedure consisted of four loading conditions (20, 40, 60, and 80 kg) that were applied in incremental order. Participants performed two trials with each load, but only the trial with the highest jump height of each load was used for further analysis. The rest period between trials with the same load was 1 min, while 3 min were implemented between different loading conditions. The CMJ technique involved the participants standing with the knees and hips fully extended, feet approximately shoulder-width apart, and the barbell resting across the back at the level of the acromion. Participants were instructed to jump as high as possible after performing a countermovement to approximately 90º of knee flexion (Garcia-Ramos et al., 2017b). Participants received jump height performance feedback immediately after each repetition and they were encouraged to jump for maximum height.

Body height (Seca 202, Seca Ltd., Hamburg, Germany) and mass (Tanita BC 418 segmental, Tokyo, Japan) were assessed at the beginning of the testing session. The loaded CMJ was performed on a Smith machine (Multipower Fitness Line, Peroga, Murcia, Spain) that restricted the movement of the barbell to the vertical direction. Three different measurement methods were used to assess the mechanical output (i.e., force, velocity, and power) under individual loading conditions as well as to determine the F-V relationship:

1. Samozino's method (SAM): CMJ height was estimated from the flight time collected by an infrared platform (Optojump, Microgate, Italy) at a frequency of 1,000 Hz. The mean values of force, velocity, and power were calculated from the equations proposed by Samozino et al. (2008). The Samozino's method only requires three input variables: system mass (sum of body mass + external load, in kg), jump height (in m) and push-off distance (in m). The push-off distance was determined as the difference between the extended lower limb length (measured from the great trochanter to toes with maximal foot plantar flexion) and the vertical distance between the great trochanter and ground with knees flexed at 90$\underset{\_}{\text{C}}$(push-off distance = extended lower limb length – vertical distance from the great trochanter to the ground). The individual value of push-off distance for each participant was maintained for all trials.

2. Force platform method (FP): the impulse-momentum approach was used to calculate force, velocity, and power output from the vertical component of the ground reaction force collected with a FP (Kistler 9253A11, Winterthur, Switzerland) (Linthorne, 2001). The sampling frequency of the FP was 1,000 Hz. The initiation of the eccentric phase was defined as the first instant when vertical ground reaction force fell 10 N below the system weight. The mean values of force, velocity, and power were obtained between the initiation (first positive velocity) and the end (take-off) of the concentric phase. The take-off was defined as the instant when ground reaction force fell below 5 N.

3. Linear velocity transducer method (LVT): A LVT (T-Force System; Ergotech, Murcia, Spain) was attached to the barbell of the Smith machine to record its velocity at a frequency of 1,000 Hz. The directly recorded barbell velocity enabled the standard software to calculate the force and power output through the inverse dynamic approach (García-Ramos et al., 2017b). The body mass of the participants was considered for force and power calculations. The mean values of force, velocity, and power were obtained between the initiation of positive velocity and the instant when the barbell's acceleration dropped to -9.81 m⋅s^-2 (Hori et al., 2007).

The mean values of force and velocity obtained under four loading conditions were used for the assessment of the F-V relationship through a linear regression: F(V) = F₀ – aV, in which F₀ represents the force intercept (i.e., force at zero velocity) and a is the slope of the F-V relationship. The maximum velocity (V₀; velocity at zero force) corresponds to F₀/a. Finally, maximum power (P₀) was calculated as P₀ = F₀·V₀/4. The magnitude of mechanical output obtained under individual loads (i.e., mean values of force, velocity, and power) and magnitude of the variables derived from the F-V relationship (i.e., F₀, V₀, F-V slope, and P₀) were compared between the three measurement methods (SAM, FP, and LVT).

Design and procedures

The force, velocity, and power output collected under different loading conditions as well as the F-V relationship were assessed during the loaded CMJ exercise within a single testing session. The outcomes provided by the three different measurement methods (SAM, FP, and LVT) were compared. Testing sessions were performed in the afternoon (16:00-19:00 hours) and under constant environmental conditions (~22$\underset{\_}{\text{O}}$C and ~60% humidity).

Statistical analysis

Data are presented as means and standard deviations, while the Pearson’s correlation coefficient (r) is presented through median values and ranges. A two-way repeated measures ANOVA (load [20 kg, 40 kg, 60 kg, and 80 kg] × measurement method [SAM, FP, and LVT]) was applied separately on each mechanical output (i.e., mean values of force, velocity, and power). The goodness of fit of the individual F-V relationships was assessed by the r coefficient. The Fisher's Z-transformed r coefficients of the individual F-V relationships were compared between the measurement methods through a one-way repeated measures ANOVA. One-way repeated measures ANOVAs were also used to compare the magnitude of the F-V relationship variables (i.e., F₀, V₀, F-V slope, and P₀) between the measurement methods. The Bonferroni post-hoc correction was considered for pairwise comparisons. Eta squared $\left({\eta }_p^2\right)$was calculated for the ANOVAs where the values of the effect sizes 0.01, 0.06 and above 0.14 were considered small, medium, and large, respectively (Cohen, 1988). Finally, the r coefficient was also used to quantify the magnitude of the association between the measurements methods for both the mechanical output obtained under individual loading conditions as well as for the F-V relationship variables. Qualitative interpretations of the r coefficients as defined by Hopkins (2002) (0 – 0.09 trivial; 0.1 – 0.29 small; 0.3 – 0.49 moderate; 0.5 – 0.69 large; 0.7 – 0.89 very large; 0.9 – 0.99 nearly perfect; 1 perfect) are provided for all significant correlations. All statistical analyses were performed using the SPSS software version 22.0 (SPSS Inc., Chicago, IL, USA) and statistical significance was set at an alpha level of 0.05.

Results

Mechanical output obtained under individual loads

The main effect of the “measurement method” was also significant for force (F = 267.8, p < 0.001, ${\eta }_p^2=0.957),$velocity (F = 300.0, p < 0.001, ${\eta }_p^2=0.962),$and power output (F = 190.0, p < 0.001, ${\eta }_p^2=0.941).$The LVT method generally provided the highest magnitude of the mechanical output, while the lowest magnitude was observed for the SAM (Figure 1). The “load” × “measurement method” interaction was also significant for force (F = 610.5, p < 0.001, ${\eta }_p^2=$0.981), velocity (F = 65.9, p < 0.001, ${\eta }_p^2=0.846),$and power output (F = 17.0, p < 0.001, ${\eta }_p^2=0.586).$The most remarkable interaction revealed a reduction in the differences between the LVT method with respect to the FP and SAM methods as the load was increased. Finally, it should be noted that the magnitude of the correlations for force, velocity, and power output between the different measurement methods were very large (Table 1).

Figure 1.

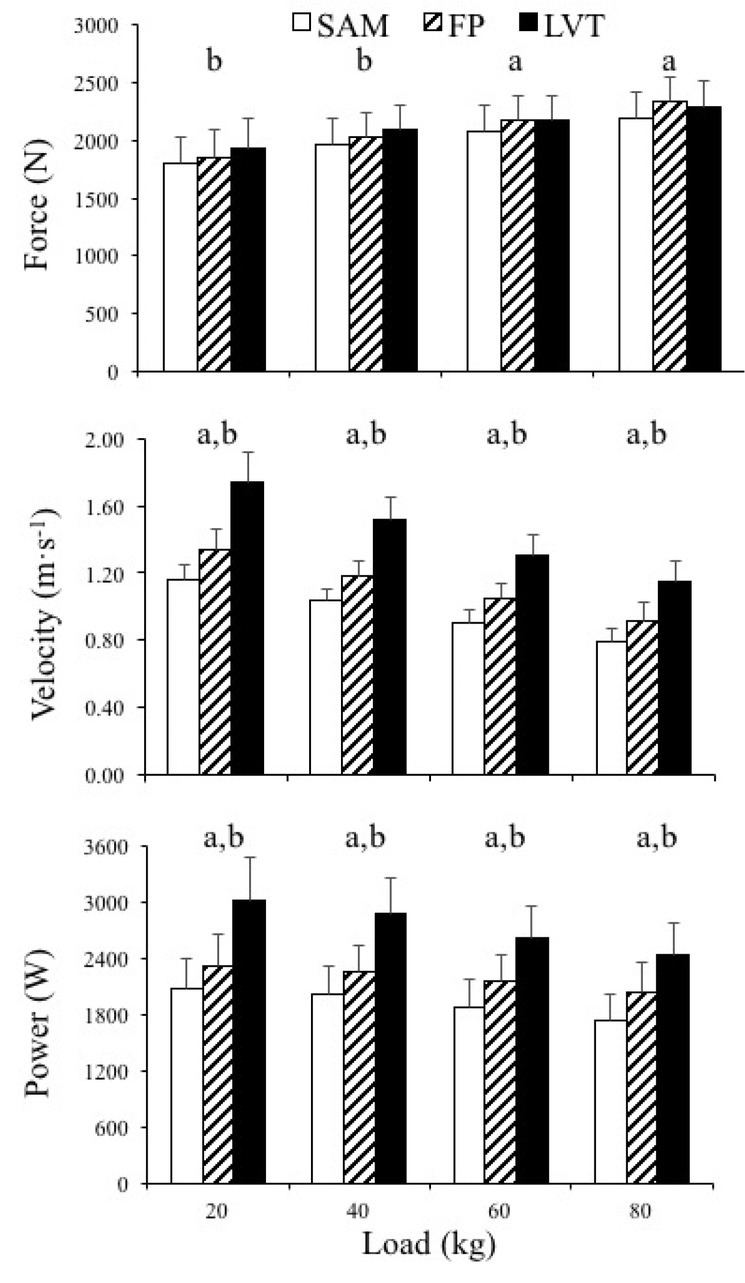
Differences in force (upper panel), velocity (middle panel), and power output (lower panel) between the Samozino's (SAM), force plate (FP), and linear velocity transducer (LVT) methods under individual loading conditions. a, SAM significantly lower than FP and LVT; b, LVT significantly higher than FP and SAM. Results depict the data averaged across the subjects with standard deviation error bars.

Table 1.

Correlations between the mean values of force, velocity, and power obtained from different measurement methods at four individual loads.

		20 kg		40 kg		60 kg		80 kg
		FP		LVT	FP	LVT	FP	LVT	FP	LVT
	SAM	0.88		0.93	0.88	0.90	0.92	0.89	0.92	0.86
Force	FP			0.99		0.95		0.99		0.93
	SAM	0.82		0.89	0.83	0.83	0.83	0.77	0.77	0.68
Velocity	FP			0.93		0.94		0.94		0.94
	SAM	0.86		0.93	0.87	0.85	0.89	0.85	0.88	0.77
Power	FP			0.95		0.92		0.95		0.90

SAM, Samozino's method; FP, force plate; LVT, linear velocity transducer. All correlations reached statistical significance (p < 0.05).

Force-velocity relationship variables

The goodness of fit of the individual F-V relationships significantly differed between the measurement methods (F = 4.7, p = 0.019, ${\eta }_p^2=$0.282). Although Bonferroni post-hoc comparisons failed to show significant differences, the measurement methods could be ranked as follow based on the strength of the F-V relationship: SAM (r = 0.985 [0.957, 0.999]) = FP (r = 0.969 [0.938, 0.996]) = LVT (r = 0.960 [0.879, 0.998]). The magnitude of the F-V relationship variables significantly differed between the measurement methods: F₀ (F = 9.9, p = 0.001, ${\eta }_p^2=0.451),$V₀ (F = 33.3, p < 0.001, ${\eta }_p^2=0.735),$F-V slope (F = 26.9, p < 0.001, ${\eta }_p^2=0.691),$and P₀ (F = 56.6, p < 0.001, ${\eta }_p^2=$0.825) (Figure 2). Finally, while large to very large correlations between the measurement methods were observed for F₀ and P₀, no significant correlations were observed for V₀ and the F-V slope.

Figure 2.

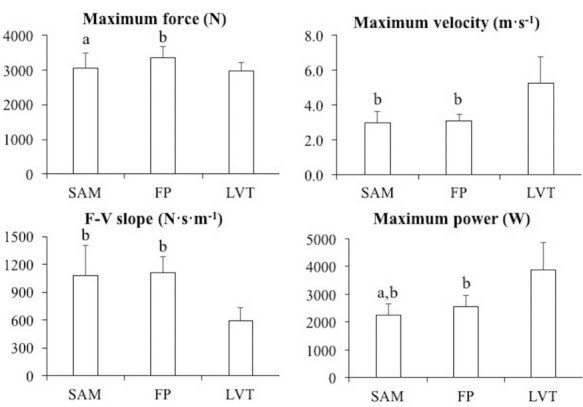
Comparison of the magnitude of the force-velocity relationship parameters obtained from the Samozino's (SAM), force plate (FP), and linear velocity transducer (LVT) methods. a, significantly different than FP; b, significantly different than LVT. Results depict the data averaged across the subjects with standard deviation error bars.

Table 2.

Correlations between the maximum force, velocity, and power parameters obtained from force-velocity relationships calculated using different measurement methods.

	F0		V0		F-V slope		P0
	FP	LVT	FP	LVT	FP	LVT	FP	LVT
SAM	0.72**	0.57*	0.34	0.43	0.29	0.34	0.70**	0.85**
FP		0.50		0.48		0.19		0.83**

SAM, Samozino's method; FP, force plate; LVT, linear velocity transducer; F₀, maximum force; V₀, maximum velocity, F-V slope, slope of the force-velocity relationship; P₀, maximum power. Significant correlations: * p < 0.05, ** p < 0.01.

Discussion

The present study was designed to explore the differences in the F-V relationship between three measurement methods commonly utilised during the routine testing of mechanical capacities of leg muscles and, with small adaptations, other muscles. The main findings regarding the mechanical output collected under individual loads revealed that, in comparison with the FP data, the LVT and SAM methods overestimated and underestimated the magnitude of the mechanical output, respectively. While the overestimation of the LVT was more prominent under light loading conditions, the differences between the FP and SAM methods were more consistent across the loads. As a consequence, the F-V slope obtained by the LVT method significantly differed with respect to the F-V slope obtained by the SAM and FP methods. The most remarkable difference regarding the magnitude of the F-V relationship variables was the higher V0 obtained from the LVT method compared to the SAM (77.1%) and FP (72.3%) methods. Although the linearity of the F-V relationship was high for the three measurement methods (r ≥ 0.96), the weakest linearity was observed for the LVT method. Taken together, while these results support the use of the SAM and FP methods to determine the F-V relationship during the CMJ exercise, they may compromise the use of the LVT due to an overestimation of V0 and a weakest linearity of the F-V relationship. However, the very large correlations observed between the three measurement methods also suggest that all of them can be used for assessing the mean values of force, velocity, and power under the applied loading conditions (Table 1).

The results of the present study are in line with previous studies that showed an overestimation of the mechanical output recorded by the LVT in comparison with the FP method (Cormie et al., 2007a; Crewther et al., 2011; Hori et al., 2007). Our results also confirmed that the overestimation of the LVT was more prominent under light loading conditions (García-Ramos et al., 2016b; Pérez-Castilla et al., 2017a). On the other hand, this was the first study exploring the differences in the magnitude of the F-V relationship variables between the FP and LVT methods during vertical jumps. The main finding revealed a 72.3% higher V0 for the LVT compared to the FP, while F0 was a 12.9% higher for the FP. As a consequence, an 86.9% difference in the magnitude of the F-V slope was observed between both measurement methods with the LVT providing a velocity-oriented F-V profile. In this regard, it should be noted that there may exist an optimal balance between F0 and V0 capacities (i.e., the F–V slope) that maximizes unloaded vertical jump performance for a given value of P0 (Jiménez-Reyes et al., 2014; Samozino et al., 2014, 2012). Therefore, the F-V relationship assessed by a LVT during vertical jumps may not be appropriate for implementing individualized resistance training programs based on the optimal F-V profile (Morin and Samozino, 2016).

Unlike the absence of significant differences reported by Jimenez-Reyes et al. (2017b), in the present study we observed a systematic underestimation in the magnitude of the mechanical output (i.e., force, velocity, and power output collected under individual loads) obtained with the SAM compared to the FP method. However, it should be noted that while Jimenez-Reyes et al. (2017b) used a FP to estimate the jump height needed for the application of the SAM, we estimated the jump height from the flight time recorded by an infrared platform. It is known that infrared platforms underestimate jump height as compared to FP measurements (Glatthorn et al., 2011). Therefore, it is possible that the underestimation of jump height was in part responsible for the lower mechanical output observed for the SAM in our study. Given that the absolute underestimation of jump height should be approximately consistent across the loads, its effect should be more pronounced under heavy loading conditions since the jump height is lower. This assumption could be supported by the significantly lower value of F0 obtained for the SAM compared to the FP method, while no significant differences were observed for V0. Therefore, researchers and coaches must consider the problem of using the jump height estimated from an infrared platform for an accurate application of the SAM.

The results of the present study are in line with previous research showing that the F-V relationship of functional tasks (e.g., vertical jumps, cycling, bench press, etc.) is highly linear (Djuric et al., 2016; Garcia-Ramos et al., 2016a; Jiménez-Reyes et al., 2017; Pérez-Castilla et al., 2017b; Zivkovic et al., 2017). The validity of the SAM could be further supported by its higher linearity (r = 0.99) compared to the FP (r = 0.97) and LVT (r = 0.96) methods. The higher linearity of the F-V relationship obtained from the SAM could be expected since it is known that countermovement depth presents minor effects on jump height, but it meaningfully affects force output (Mandic et al., 2015). Therefore, while the possible variation in countermovement depth during the testing protocol could compromise the linearity of the F-V relationship obtained from the FP and LVT data, the SAM should not be affected since it relies on vertical jump height. In general, the high linearity of the F-V relationship supports the two-load method proposed by Jaric (2016) (i.e., the F-V relationship modelled from the force and velocity data collected under only two loading magnitudes).

The very large correlations observed between the three measurement methods (i.e., SAM, FP, and LVT) for the mean values of force, velocity, and power support their validity for the assessment of mechanical output under the applied loading conditions. The high correlations between these measurement methods are in line with previous studies (Giroux et al., 2014; Jimenez-Reyes et al., 2017b; Pérez-Castilla et al., 2017a). However, the systematic differences observed in the magnitude of the mechanical output also confirm that these measurements methods should not be used interchangeably (Cormie et al., 2007a; García-Ramos et al., 2016b; Lake et al., 2012). Finally, it should be noted that while the magnitude of F0 and P0 was significantly correlated between the three measurement methods, no significant correlations were observed for V0 or the F-V slope. The large extrapolation needed to reach V0 from the experimental data could be responsible for such a finding since it is known that the accuracy of the F-V relationship is compromised when the experimental points are far from the axis intercepts (Pérez-Castilla et al., 2017b). In this regard, the inclusion of unloaded vertical jumps should be recommended for a more precise assessment of the F-V relationship during the routine testing of maximal capacities of leg extensors muscles to produce force, velocity, and power (Cuk et al., 2014).

In conclusion, large differences were observed in the magnitude of mechanical output obtained under individual loads as well as in the F-V relationship when they are collected by a LVT in comparison with the SAM and FP methods. The higher overestimation of velocity output by the LVT under light loading conditions resulted in a velocity-oriented F-V profile compared to the SAM and FP methods. These results could compromise the validity of the F-V relationship obtained with a LVT attached to the barbell during vertical jumps. On the other hand, similar F-V profiles were obtained by the SAM and FP methods. It should be noted that the lower mechanical output observed for the SAM method compared to the FP was probably caused because the CMJ height used for the application of Samozino's equations was obtained from an infrared platform which is known to underestimate jump height. Therefore, although both the SAM and FP methods could be recommended for assessing the F-V relationship during the CMJ exercise, for an accurate application of the SAM it would be preferable to use measurement methods that do not underestimate jump height (e.g., force platforms or high-speed cameras). The very large correlations observed between the three measurement methods (i.e., SAM, FP, and LVT) for the mean values of force, velocity, and power support their validity for the assessment of mechanical output under the applied loading conditions.