Abstract
Recently, mass spectrometry (MS) has become a viable method for elucidation of protein structure. Surface-induced dissociation (SID), colliding multiply charged protein complexes or other ions with a surface, has been paired with native MS to provide useful structural information such as connectivity and topology for many different protein complexes. We recently showed that SID gives information not only on connectivity and topology but also on relative interface strengths. However, SID has not yet been coupled with computational structure prediction methods that could use the sparse information from SID to improve the prediction of quaternary structures, i.e., how protein subunits interact with each other to form complexes. Protein–protein docking, a computational method to predict the quaternary structure of protein complexes, can be used in combination with subunit structures from X-ray crystallography and NMR in situations where it is difficult to obtain an experimental structure of an entire complex. While de novo structure prediction can be successful, many studies have shown that inclusion of experimental data can greatly increase prediction accuracy. In this study, we show that the appearance energy (AE, defined as 10% fragmentation) extracted from SID can be used in combination with Rosetta to successfully evaluate protein–protein docking poses. We developed an improved model to predict measured SID AEs and incorporated this model into a scoring function that combines the RosettaDock scoring function with a novel SID scoring term, which quantifies agreement between experiments and structures generated from RosettaDock. As a proof of principle, we tested the effectiveness of these restraints on 57 systems using ideal SID AE data (AE determined from crystal structures using the predictive model). When theoretical AEs were used, the RMSD of the selected structure improved or stayed the same in 95% of cases. When experimental SID data were incorporated on a different set of systems, the method predicted near-native structures (less than 2 Å root-mean-square deviation, RMSD, from native) for 6/9 tested cases, while unrestrained RosettaDock (without SID data) only predicted 3/9 such cases. Score versus RMSD funnel profiles were also improved when SID data were included. Additionally, we developed a confidence measure to evaluate predicted model quality in the absence of a crystal structure.
Short abstract
A surface-induced dissociation (SID) appearance energy (AE) provides a single restraint that can improve model selection of protein complex structures from protein−protein docking.
Introduction
Since the invention of electrospray ionization (ESI)1 and other advances, mass spectrometry (MS) has been used to determine the mass2,3 and oligomeric distribution4 of protein assemblies. Among the benefits of MS are the ability to handle small sample sizes (μLs of sample, at low μM concentrations or lower), complex samples, samples that cannot crystallize, and both small and large proteins (up to megadalton sized assemblies). More recently, MS has been demonstrated as an efficient analytical tool to yield three-dimensional structural information on proteins and their molecular complexes.5,6 Several methods have been successfully coupled with MS to elucidate structural information. Ion mobility mass spectrometry (IM/MS)7−10 allows for the separation of protein complexes based on size, charge, and shape. In IM/MS, complexes are ionized and accelerated through a bath gas. The time needed for the ions to pass through the bath gas is dependent on their sizes/shapes as their movement is hindered by collisions with the gas molecules. These time measurements are then translated into rotationally averaged collisional cross sections that provide insight into the shape of the complex. Chemical cross-linking11−13 uses reagents, such as disuccinimidyl sulfoxide (DSSO),14 to chemically link residues that are located spatially near each other. Cross-linked protein complexes are then enzymatically digested and analyzed with MS, providing useful residue–residue distance restraints. Covalent labeling15 methods chemically alter (i.e., change the mass of) residues that are more solvent-exposed in solution before the proteins are digested and analyzed with MS. Many different techniques exist to alter the mass of solvent-exposed residues. Covalent labeling methods can be largely separated into two groups, namely, specific and nonspecific labeling methods. Nonspecific labeling methods can label most, if not all, types of amino acid residues. Commonly used nonspecific labeling methods are hydrogen–deuterium exchange (HDX)16,17 and oxidative footprinting methods such as fast photochemical oxidation of proteins (FPOP).18,19 In contrast, specific labeling methods target particular amino acids, or types of amino acids. Common methods can target arginine, carboxylic acids, cysteine, histidine, lysine, tryptophan, and tyrosine.15
Other MS-based methods gain insight into protein complex structure by dissociating protein complexes by collision with a gas or a surface, collision-induced dissociation (CID)20,21 and surface induced dissociation (SID).22−25 In both activation methods, protein complexes are multiply charged by a soft ionization method (typically nanoelectrospray ionization) and transferred into the gas phase, preserving quaternary structure,26,27 and then accelerated toward a collision medium. The difference in the two methods is the medium of the collision. In CID, complexes collide with many inert gas atoms or molecules, whereas in SID, complexes collide with a surface, typically a self-assembled monolayer of fluorinated alkanethiol on gold. For both methods, upon collision with the target, noncovalent protein–protein interfaces in the complex can break apart, rendering individual subunits or subcomplexes (monomers, dimers, trimers, etc.). MS is then used to determine relative intensities of each oligomer. In CID, the observed dissociation pathway frequently results in the ejection of highly charged monomers (indicative of subunit unfolding),28 while SID usually provides a profile of connectivity based on ejection of specific nativelike subcomplexes.29 Although unfolding is frequently observed in CID, it is possible in some cases to influence this process such that unfolding is alleviated so that structural inter-subunit connectivity can be determined.30 Conversely, SID typically gives extensive information on structural connectivity, from which data have been favorably compared to known crystal structures on many systems.22,24,31−34 Typically, SID has been used to elucidate complex stoichiometry and connectivity. However, we recently demonstrated a strong correlation between appearance energy (AE) and structural features of dissociated interfaces using SID.35 While SID, along with other bioanalytical MS and dissociation techniques, yields useful structural information, the data are still sparse, not allowing for an unambiguous determination of the protein complex structure. In fact, the data extracted from SID measurements for use in this study contained only a single data point for each interface, the AE. For this reason, there remains a critical need for computational methods that can facilitate structural interpretation of SID data.
Numerous experimental techniques (outside of MS) that also yield sparse data have been successfully combined with computational methods to facilitate structure determination of individual proteins. Sparse data from nuclear magnetic resonance (NMR), namely, chemical shifts, orientational restraints from residual dipolar couplings (RDC), and distance restraints from the nuclear Overhauser effect (NOE), have been coupled with Rosetta (CS-Rosetta)36−39 to successfully predict protein folds. Similarly, TOUCHSTONEX uses sparse long-range contacts derived from NOE to fold proteins.40 Site-directed spin labeling electron paramagnetic resonance (SDSL-EPR) data can also be used in Rosetta (RosettaEPR)41,42 and BCL:MP-Fold43 to improve high-resolution structure prediction through protein folding and homomer structure generation.44 Additionally, small angle X-ray scattering (SAXS) profiles can be used to refine (FoXS) and predict (MultiFoXS) protein folding as well as to predict complex structures through rigid protein–protein docking (FoXSDock).45 SAXS can also be used with course grained molecular dynamics (MD) for structure prediction.46 Finally, cryoelectron microscopy (cryoEM) density maps (medium and high resolution) can be used in EM-Fold,47−49 Rosetta,50−52 molecular dynamics (MD),53−58 and Pathwalking.59
For the computational structure prediction of protein complexes, protein–protein docking is often used. Protein–protein docking methods, such as DOT,60 HADDOCK,61 ZDOCK,62 ClusPro,63−65 and PatchDock/SymmDock,66 take all-atom subunit structures as inputs and predict the relative orientation of the subunits in the complex. Rosetta’s protein–protein docking algorithm, RosettaDock,67 uses Monte Carlo sampling techniques with Rosetta’s scoring function.68 RosettaDock has two main docking phases, low-resolution centroid followed by high-resolution all-atom. In the low-resolution phase, residues are represented as single spheres (centroid mode) while, in the high-resolution phase, all atoms are explicitly represented (all-atom mode). Improvements made in RosettaDock include more efficient and accurate side-chain rotamer optimization,69 inclusion of backbone flexibility,70,71 allowing for differences in pH,72 and modeling of water-mediated interfaces.73 Although RosettaDock has been very successful, improvements are always beneficial.
In the field of MS, chemical cross-linking74 and covalent labeling methods75 have been used in Rosetta to provide useful distance and exposure restraints for de novo modeling and protein–protein docking to improve prediction. Outside of Rosetta, the Integrative Modeling Platform76−78 has had tremendous success at predicting several protein complex structures using multiple types of MS data such as ion mobility,10,79 chemical cross-linking,80−86 and covalent labeling.87 Other platforms can also use cross-linking data to model structures (Xlink DB 2.0,88 Xlink Analyzer,89 XL-MOD,90 DynaXL,91 and HADDOCK92). Recently, HDX has also been used in combination with protein–protein docking using DOT.93 However, SID data have not yet been used to facilitate structure prediction. Recently, a correlation between SID appearance energy and protein–protein interface properties along with intra-subunit rigidity has been demonstrated;35 however, a link to structure prediction is missing.
In this work, we developed an improved model to use structural features of protein–protein interfaces to predict SID AE specifically for use in protein–protein complex structure prediction. Next, we developed a Bayesian scoring function that combines Rosetta’s protein–protein docking scoring function with an SID scoring term that assesses agreement of protein complex structures with experimental SID AE, penalizing structures with high disagreement from experiment. Finally, we showed that using this scoring function to rescore poses generated from RosettaDock improved the selection of nativelike models. The SID_rescore application is freely available and easily accessible through Rosetta. We developed confidence measures that distinguish successful predictions from unsuccessful ones. In a benchmark of nine protein complexes, our method predicted 6/9 structures with root-mean-square deviation (RMSD) less than 2 Å from the native (as compared to 3/9 with Rosetta only).
Results and Discussion
Improved Model More Stable Using Hydrophobic Surface Area
In previous work,35 we developed a model to predict SID AE of any protein–protein interface (PPI) based on structural features of the specific PPI. While SID AE is a gas-phase measurement rather than a solution-phase restraint, our previous study highlighted that this measurement can be correlated with solution-phase structural properties. The previously reported model used a linear combination of the number of interacting residues at the interface (NR), number of unsatisfied hydrogen bonds at the interface (UHB), and intra-subunit rigidity (RF, see below). Although this model showed a strong correlation between calculated and experimental AE, it was not ideally suited for protein complex structure prediction. We found that poses with low interface RMSDs can have drastically different UHB and thus AEpred, rendering UHB problematic for use in protein−protein docking where it is necessary to consistently assign favorable scores to near-nativelike structures. For this reason, a slightly modified model, consisting of NR, RF, and hydrophobic surface area (HSA) of the interface (eq 1), was more successful for structure prediction. The substitution of HSA (replacing UHB) allowed for stable use of the model in protein–protein docking. We hypothesized that this model could be used for structure prediction of protein complexes from SID data. Because the model can predict AE based on the structure, it could be used to evaluate an ensemble of predicted structures in situations where the AE is known from SID experiments. To do this, we developed an SID scoring term to be used in combination with the RosettaDock scoring function for the evaluation of poses from protein–protein docking.
Use of the Predictive Model and Rosetta SID Scoring Function Can Improve Model Selection with Ideal Data (AE Predicted from Crystal Structures)
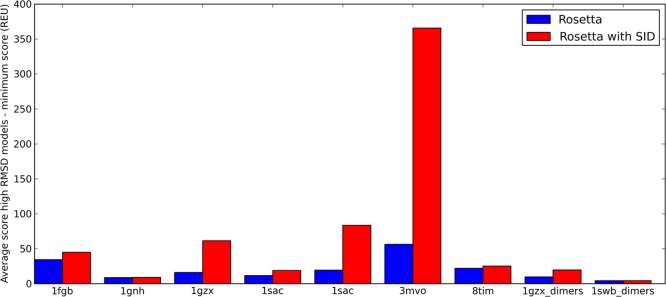
To explore whether the predictive model containing HSA, NR, and RF theoretically provides sufficient information to successfully discriminate between protein complex models generated by protein–protein docking, we first tested the scoring function on a large number of docking cases using ideal data: rather than using SID AE from experimental data, the crystal structures of 57 proteins (list of complexes shown in Table S1) were used to generate theoretical appearance energies (using the predictive model) for the interface between two subunits. We investigated complexes consisting of dimers (homo and hetero), tetramers, and pentamers of 100–450 residues per chain in size. In each case, the calculated AE was treated identically to the experimental AE for rescoring experiments. For each complex, 10 000 potential structures (poses) were generated using RosettaDock. A randomization flag ensured that the docking sampled many different orientations of protein–protein interfaces. All poses were rescored using the developed Rosetta SID scoring function. The rescoring results were evaluated on the basis of the best RMSD in the top three scoring models, as shown in Figure 1. Out of the 57 complexes tested, the RMSD of the selected structure either improved or stayed the same for 54 cases when the ideal SID AE data (predicted from crystal structures) were incorporated. An undesirable increase in RMSD of more than 1.5 Å was observed for only one case. For 14 complexes, the RMSD improved (decreased), and for 10 complexes, the RMSD improved (decreased) by more than 10 Å when predicted AE data were used for the rescore. Figure S1 shows predicted structures for five cases where including the ideal AE data significantly improved model selection (3VM9, 3GMX, 3JCF, 4IX2, and 4HY3). The funneling of these score versus RMSD distributions also improved significantly, as will be described later. These results may not be fully representative of a realistic application of experimental SID AEs since the data used for these complexes were essentially assuming a perfect predictive model. However, as a proof of principle, they do show that knowing the information contained in the model (HSA, NR, and RF) has strong potential to successfully assist with the discrimination between good and poor protein–protein docking poses.
Figure 1.
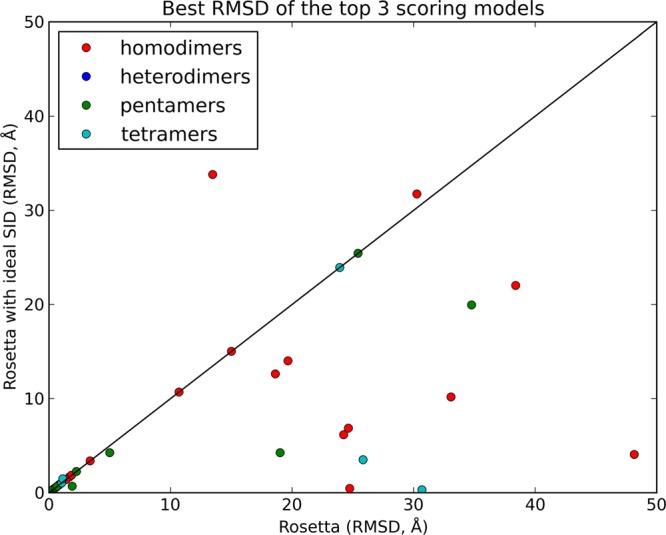
Comparison of rescoring results for docking cases using ideal SID AE data. For each of the 57 complexes, 10 000 poses were generated using RosettaDock and rescored using the Rosetta/SID scoring function. The best RMSD in the top 3 scoring models is shown with and without the incorporation of SID data. The selected structure improved or stayed the same for 54 cases, and in only one case, an undesirable increase of more than 1.5 Å was observed. Additionally, 10 cases improved by more than 10 Å.
Bayesian SID Scoring Function Improves Protein–Protein Docking Model Selection
Nine protein complexes, which were all substructures (frequently dimers contained within the full complexes) of the protein complexes in the SID data set (as described in the SI), were used to assess whether SID data can be used to improve protein complex structure prediction. It is important to note that all SID experiments were performed under “charge-reducing” conditions, which are thought to keep the complex more compact and nativelike.94−96 In addition, to avoid collapse or unfolding, the instrument was tuned to limit activation in regions where activation is not intended, i.e., in regions other than the SID device. We have previously reported differences in SID AE if the structure has been preactivated (e.g., by in-source CID97). In addition, we would anticipate differences between experimental and theoretical measurements if disruptive organic solutions were added to the sample, so those were avoided. Although it is not expected that gas-phase measurements are providing direct information on solution-phase structures, it is likely that the complexes are kinetically trapped with interfaces intact. SID in the gas phase can then disrupt the kinetically trapped structure with its structurally informative interfaces in such a way that the AE data can be used to predict which computationally docked structure is the best fit to the solution structure.
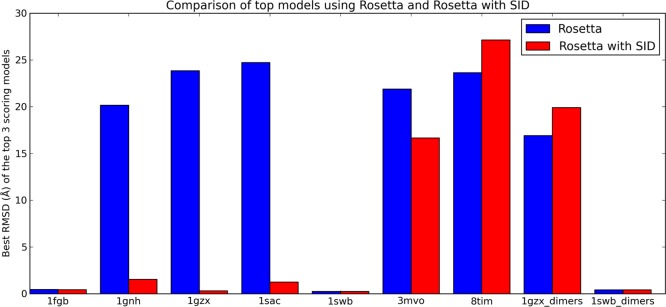
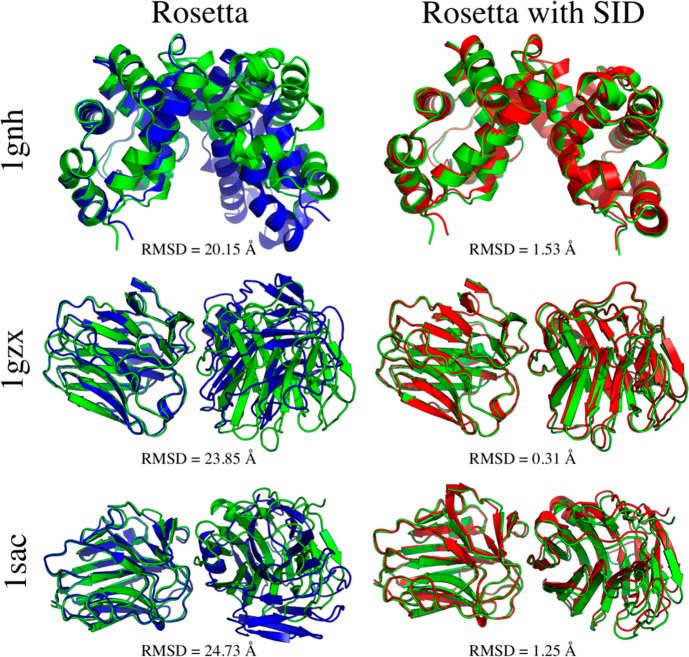
For each subcomplex, 10 000 poses were generated using unrestrained RosettaDock, using an initial randomization flag. Subsequently, all RosettaDock poses were additionally rescored using the developed Bayesian SID scoring function to compare its ability to identify nativelike poses to that of the Rosetta protein–protein docking scoring function. On the basis of this analysis, the AE prediction model (eq 1) was ultimately tested on 90 000 poses. Figure S2 shows the SID score versus RMSD plots for 1GZX, 1SWB, 1SAC, and 1GZX_dimers. In general, the SID scoring term scored low-RMSD structures well while penalizing most high-RMSD structures. This term (based on agreement with SID AE) was not able to unambiguously select nativelike structures alone but, when combined with the RosettaDock scoring function, showed significant improvement in model selection. Figure 2 shows the results from the docking and rescoring with the Rosetta/SID combined scoring function. In 6/9 cases, the best RMSD of the top three scoring models was less than 2 Å with respect to the native structure using the Bayesian SID score (1FGB, 0.43 Å; 1GNH, 1.5 Å; 1GZX, 0.31 Å; 1SAC, 1.25 Å; 1SWB, 0.23 Å; 1SWB_dimers, 0.41 Å). For Rosetta alone, only 3/9 cases resulted in structures with less than 2 Å RMSD (1FGB, 0.44 Å; 1SWB, 0.23 Å; 1SWB_dimers, 0.41 Å). In three cases where Rosetta predicted poorly (1GNH, 1SAC, 1GZX), SID was able to drastically improve selection, decreasing the RMSD by >18 Å for each structure shown in Figure 3 (18.6, 23.5, and 23.5 Å, respectively). Additionally, the average RMSD of the top 100 scoring structures was lower (or equal) for the Rosetta/SID scoring function than for the Rosetta score alone for 8/9 cases (Table S2).
Figure 2.
Comparison of Rosetta and Rosetta with SID. For each subcomplex, 10 000 structures were generated using unrestrained RosettaDock and rescored using the developed Bayesian SID docking score (which is a linear combination of the RosettaDock score and a developed SID score). For each of the nine subcomplexes, the lowest RMSD among the top three scoring structures is shown. Rosetta with SID showed an improved ability over the RosettaDock score to identify nativelike structures within the top three scoring models. In 6/9 cases, the pose with the best RMSD of the top three scoring poses from Rosetta with SID was within 2 Å from the native while only 3/9 cases using RosettaDock gave sub-2 Å RMSD models.
Figure 3.
Docked complexes of the subcomplexes for which including SID restraints improved RMSD by more than 18 Å. Green structures are the natives, blue the models predicted without SID data, and red the models predicted with the Bayesian Rosetta SID rescore. For each dimer, the stationary subunit (left) was aligned to show the discrepancy or lack thereof for the mobile (docked) subunit (right).
Confidence Measure Allows Identification of Systems with Nativelike Models
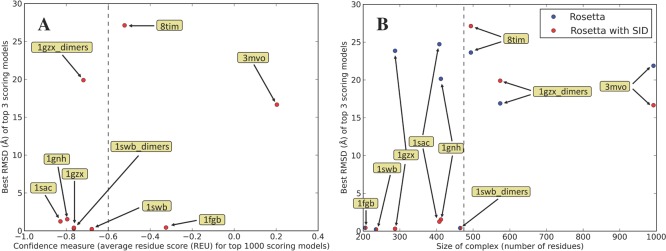
While the Bayesian SID scoring function correctly identified a near-native structure among the top scoring models for 6 out of 9 benchmark proteins, it did not achieve this for 3 of the proteins. We thus investigated whether it was possible to identify a confidence measure that selectively flags successful benchmark cases in the absence of a crystal structure. To assess the confidence in the results from protein to protein, we examined the average score per residue of the top 1000 scoring structures from each of the complexes that were docked. Structures with low score per residue can be considered lower energy and more nativelike; thus, confidence in these structures is higher. Figure 4A shows RMSD (corresponding best RMSD of the top 3 scoring models from Figure 2) versus average score per residue of the top 1000 models when SID was used to rescore. Proteins with lower score per residue correspond to higher confidence in the structures built, as they can be considered more nativelike. This confidence measure naturally separates the proteins into two groups, high confidence [systems with average score per residue lower than −0.6 REU (Rosetta Energy Unit, dotted line)] and low confidence (systems with average score per residue higher than −0.6 REU). According to this measure, 5/6 of the high-confidence proteins had low RMSDs (less than 2 Å) while 2/3 of the high-RMSD models were flagged as low-confidence proteins. Despite the high RMSD, the high-confidence outlier (1GZX_dimers) did improve dramatically, increasing Pnear 42-fold and improving the ranking of the lowest-RMSD pose (from 1286 to 51). Thus, the investigated confidence measure allowed for successful identification of low-RMSD models when it was used to examine the structures predicted with Rosetta and SID.
Figure 4.
(A) Best RMSD of the top three scoring poses when SID data were included, shown against the confidence measure of average residue score for the top 1000 scoring poses. High-confidence (to the left of the dotted line) structures performed well with SID, while all poor structures are considered low-confidence (to the right of the dotted line). (B) Prediction results dependence on protein size. SID helped to correctly predict (within 2 Å RMSD of native) all complexes smaller than 475 residues, while RosettaDock failed to correctly predict half of the complexes smaller than 475 residues without SID data.
SID Data Most Useful in Predicting Smaller Complexes
With any form of protein structure prediction, accuracy typically scales inversely with size, where smaller proteins are generally predicted more accurately.98 To investigate the influence of size on prediction accuracy in our benchmark, we measured the size of the complex in terms of the total number of residues of the subunits involved in the interface. When SID was used to rescore structures, much like with the previously mentioned confidence measure, size strongly correlated with accuracy. Figure 4B shows that all complexes with fewer than 475 residues were correctly predicted (RMSD < 2 Å), while all larger complexes performed poorly. SID strongly improved the prediction accuracy over RosettaDock alone, which failed to accurately predict the structure of three of the complexes with fewer than 475 residues.
Improvement in “Goodness of Funneling”
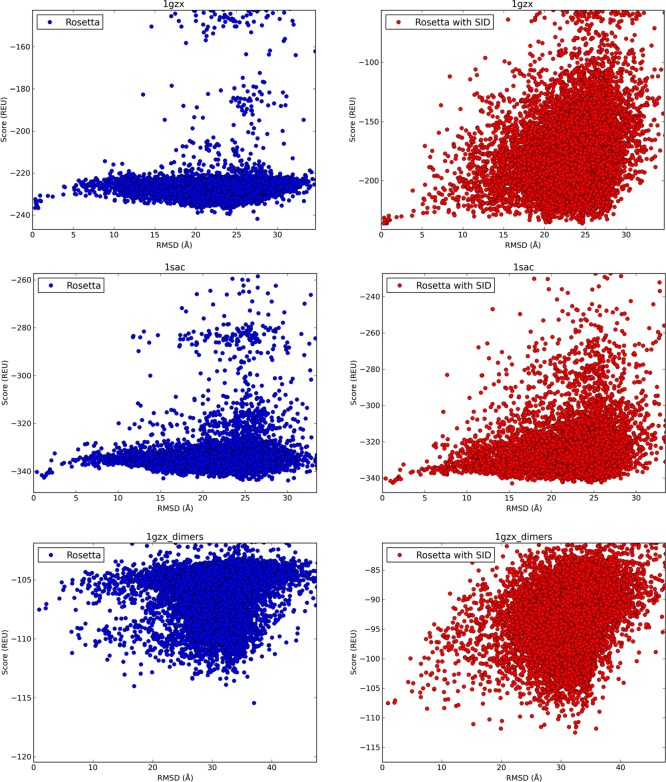
Not only did SID improve model selection, but it also improved the “goodness of funneling” in the score versus RMSD plots. This is generally achieved when low-RMSD (i.e., more nativelike) structures tend to score better on average than high-RMSD structures resulting in a funnel-like shape in the score versus RMSD plot. To quantify this, we used the metric Pnear,99 which ranges from zero (poor funneling) to one (good funneling). The calculated Pnear values can be found in Table S3. In three of the nine tested cases (1GZX, 1SAC, and 1GZX_dimers), there was a greater than 3-fold increase in funneling between the Rosetta scored models and the Rosetta/SID scored models (42.2, 3.68, and 42.4, respectively). Figure 5 shows the score versus RMSD plots for these cases. For two out of the three protein complexes that showed large increases in Pnear, SID also dramatically improved RMSD (from 23.9 to 0.31 Å for 1GZX, and from 24.7 to 1.25 Å for 1SAC). Even though Rosetta/SID did not predict a structure with RMSD lower than 2 Å for 1GZX_dimers, the increase in Pnear (as compared to Rosetta alone) is an indication of significant improvement over Rosetta alone. For this protein, the top generated pose (RMSD = 0.94 Å) ranked 1286/10 000 in score using Rosetta but improved to 51/10 000 using Rosetta with SID data. Additionally, the Pnear also improved for 56/57 ideal cases (except 4IWH) when SID data were used, as shown in Figure S3A.
Figure 5.
Score vs RMSD plots of each complex for which Pnear (quantification of “goodness of funneling”) increased by greater than 3-fold (absolute values in Table S3) when SID data were used. 1GZX, 42.2-fold increase; 1SAC, 3.68-fold increase; 1GZX_dimers, 42.4-fold increase.
Another way to assess funneling is to examine the scores of the high-RMSD structures. If the scores of high-RMSD structures are increased, then a score versus RMSD profile can be considered more “funnel-like.” More specifically, if high-RMSD structures are separated by a larger score difference (on average) from the lowest score, then funneling is increased. Using this criterion, rescoring with SID again showed improvement. Figure 6 shows the difference between the average score of all high-RMSD structures (RMSD > 10 Å) and the lowest score with the RosettaDock score and Rosetta/SID rescore. For each complex, there was a larger separation in score from the minimum for the high-RMSD structures when SID data were included. This indicates that the developed SID scoring term successfully penalized (i.e., increased the score of) high-RMSD structures as compared to the RosettaDock total score. For the ideal docking data, this metric improved for all 57 cases when SID data were incorporated, as shown in Figure S3B.
Figure 6.
Separation of the average score high-RMSD models (RMSD > 10 Å) from the minimum score for each docked subcomplex with and without SID data. For each complex, high-RMSD structures are penalized more when SID data were included.
Lack of Sampling Can Help Explain Suboptimal Prediction Results for Three Complexes
Although SID data helped to successfully identify low-RMSD structures (<2 Å RMSD) for 6/9 complexes, for three complexes (1GZX_dimers, 3MVO, and 8TIM), this was not the case. These three complexes were all relatively large (Figure 4B), and our confidence measure (average score of the top 1000 scoring models) was also relatively poor (Figure 4A). For 1GZX_dimers, there was a significant improvement in funneling when SID was used (42-fold improvement in Pnear). Considering Figure 5 for the score versus RMSD plot, the scoring ranking of the lowest-RMSD structure improved (from 1286/10 000 to 51/10 000). Thus, despite the fact that the predicted structure did not improve for this protein, SID did show improvement in the overall scoring of candidate structures. For both 3MVO and 8TIM, we suspect that the poor predictions may be largely due to poor sampling, which is often exacerbated for large complexes due to the large conformational search space. Interestingly, these two were the only complexes for which no structure with less than 4 Å RMSD was observed from the docking. Specifically for the 3MVO case, the poor sampling is likely due to the intertwining nature of the monomers at the interface, which might necessitate unfolding followed by restructuring to bind in nature. Since the sampling of structures was independent of the SID scoring term, it is difficult to assess whether the shortcoming of the prediction was due to the inclusion of SID data. In addition to the poor docking prediction for these two structures, they also both had considerably worse Pnear values when SID was used (score versus RMSD plots are shown in Figure S4). However, the absolute Pnear values from RosettaDock alone were also extremely low (1.77 × 10–14 and 1.06 × 10–4, respectively), so the decreases may not be as meaningful in these cases. On the contrary, the funneling metric used in Figure 6, the average separation between high-RMSD poses (>10 Å) and the minimum scoring pose, showed improvement for both 8TIM (from 22.0 to 25.2 REU) and 3MVO (from 56.3 to 365.6 REU), indicating that high-RMSD poses were generally penalized more than low-RMSD poses. Despite the fact that Rosetta with SID did not predict nativelike structures in all cases, addition of the SID-dependent term was never detrimental.
Conclusion
We used a benchmark set of seven protein complexes for which SID data as well as crystal structures were available to develop a Bayesian scoring function that combined the RosettaDock scoring function with a novel SID scoring term that used the predictive model to quantitatively assess agreement with experiment for any generated structure. The aforementioned Bayesian scoring function was used to rescore poses generated from unrestrained RosettaDock. As a proof of principle, we first tested the potential effectiveness of this scoring function on 57 cases where the data were ideal (NR, HSA, and RF extracted from the subcomplex crystal structures to predict AE). Next, we tested the scoring function on 9 cases with real experimental data. In 6/9 subcomplexes tested, when SID data were incorporated, we predicted structures with less than 2 Å RMSD from the native while, without the SID restraints, we predicted those for just 3/9. SID helped correctly predict structures within 2 Å RMSD from native for 5/6 high-confidence complexes and all complexes with fewer than 475 residues. SID data also significantly improved “goodness of funneling” in some cases. From these results, we conclude that SID does provide useful structural restraints that can be employed in protein quaternary structure prediction. We hypothesize that SID helps RosettaDock identify nativelike structures based on interface size and hydrophobicity since interfaces are scored based on number of interface residues and buried hydrophobic surface area at the interface, while also using Rosetta’s successful scoring function, providing a more detailed assessment of the binding. A newly developed SID_rescore application is freely available and easily accessible through Rosetta. We further showed that, although SID AE data are not collected in the solution-phase, and protein–protein interactions can change in the gas phase (for example, strengthening of electrostatics), factors such as kinetic trapping, leading to retention of the protein–protein interfaces, do allow AE data to provide useful restraints for solution-phase structure prediction. We have added a tutorial, including a summary of necessary files and command lines, to the Supporting Information. Future work will focus on improving the method to work on larger complexes and to explore whether different protein structural motifs require different AE prediction equations. Specifically, we hope to combine SID AE with cryoEM density maps and/or other MS measurements such as ion mobility collisional cross sections, covalent cross-linking, covalent labeling, etc. Including more restraints could help improve the predictive power of SID.
Methods
Predicting Appearance Energy
Prediction of appearance energy (AE), the lowest experimental energy required to cleave the separating interface of the complex and measure it on the mass spectrometer, was described in a recent paper.35 Here, we pursued a similar strategy to improve the AE prediction for use in computational structure prediction. Rosetta’s InterfaceAnalyzer100 was used to calculate the following structural features of the native crystal structure complexes of the identified dissociating interfaces: change in Rosetta energy when subunits interact, change in Rosetta energy when subunits interact per area of interface, Rosetta energy of interface residues, Rosetta energy per residue for the interface, hydrophilic/hydrophobic/polar/total surface area of interface, salt bridges at interface, hydrogen bonds at interface, unsatisfied hydrogen bonds at interface, hydrogen bond Rosetta energy at interface, and number of interface residues. All these quantities were subsequently normalized by the number of inter-subunit protein–protein contacts. While some of the calculated interface features individually showed a correlation to AE (number of interface residues, R2 = 0.38; interface surface area, R2 = 0.35; Rosetta interface ΔG, R2 = 0.22), a model that combined several interfacial features allowed us to most accurately predict AE for any given structure based on the PPI properties. We also developed a term to account for subunit flexibility. This term, called the rigidity factor (RF), quantifies intra-subunit stability and is bounded between zero and one, where one denotes the most rigid, and zero denotes the most flexible. The RF is calculated on the basis of the density (normalization per residue) of intra-subunit hydrogen bonds, salt bridges, and disulfide bonds (full description in ref (35)). For structure prediction, the best model, after iteratively searching through combinations of the calculated parameters and RF, includes number of residues at the interface (NR), hydrophobic surface area of the interface (HSA), and RF (shown in eq 1). To optimize the weights, we used python’s simplex algorithm101 to minimize χ2 between predicted and experimental AE for the SID data set (as described in the SI).
| 1 |
Bayesian Scoring Function
To use the experimental data to derive a scoring function for protein structure prediction, the posterior probability, p(x|D), i.e., the probability of observing a particular structure given the data, was evaluated. To assess the posterior probability, Bayes’ theorem in eq 2 was used.
| 2 |
Note that the probability of observing the data (p(D), denominator) was disregarded because we considered the probabilities of many structures given the same data; thus, p(D) was a constant scaling factor. Therefore, to determine the posterior probability, we needed to define two terms: the likelihood (p(D|x)), representing the probability of measuring the data given the structure, and the prior (p(x)), representing the probability of observing the structure without considering the data. RosettaDock was used to sample the prior distribution, and thus, the prior probability is shown in eq 3.
| 3 |
The scoring function was defined as the negative logarithm of the posterior probability, shown in eq 4. For this scoring function, low scores corresponded to high probability, and high scores corresponded to low probability. Note that the systematic use of Bayes’ theorem allowed us to separate the contribution of previous knowledge (prior) and the data (likelihood), resulting in the linear combination of the two terms. In the equation, the prior score (−ln[p(x)]) is proportional to the energy of the complex, for which the RosettaDock total score was used.
| 4 |
To determine the score of the likelihood (−ln[p(D|x)]), we used the previously mentioned AE prediction model. For a given structure to be scored, the interface AE was first calculated using eq 1. Next, on the basis of the absolute deviation from the experimental AE (Δ), a fade function was used to determine the score of the likelihood, as shown in Figure S5. The function contained two cutoffs, a lower cutoff (Elow = 100 eV) below which structures were given a score of zero and a higher cutoff (Ehigh = 1750 eV) above which structures were given the maximum score. We hypothesize that the inclusion of the low cutoff (Elow) helped account for experimental uncertainty as it allowed us to treat structures that come within 100 eV of the experimental AE equally. According to this scoring term, structures with small deviation from experiment would have a low score, thus a high probability, and structures with high deviation from experiment would have a high score, thus low probability. A third parameter was introduced as a weight of this term. The final form of the Bayesian scoring function is shown in eq 5. The weights and cutoffs were optimized as part of the benchmark and thus approximate the true likelihood probability.
| 5 |
Protein–Protein Docking
To generate a large set of potential protein complex structures, RosettaDock was used. Relaxed complex crystal structures were chosen as starting structures. To avoid biasing the results and to properly perturb the subunits away from the native structure for testing purposes, the −randomize2 flag was used, which randomizes the position and orientation of the subunit to be docked.
To first test the viability of the scoring function to rank poses, 57 different complex structures were chosen from the protein databank (list of complexes shown in Table S1) containing 34 dimers (30 homo, 4 hetero), 18 homopentamers, and 5 homotetramers. For each of the 57 complexes, we docked one subunit to an adjacent subunit and generated 10 000 poses. Next, as a proof of principle, the crystal structures were used to calculate a theoretical appearance energy for those interfaces. This AE was used as a substitute for the experimental AE as an ideal case. Using these ideal SID AE data, the structures were rescored using the Rosetta SID scoring function.
For each protein in the SID data set (described in the SI), we first docked one subunit to the adjacent subunit separated by the interface identified by SID. In addition to these seven dockings, for the two tetramers, we also docked dimers together to form the tetramers since those interfaces were also known. The specific chains docked were as follows (according to chain ID’s in the PDB): 1FGB, D_E; 1SAC, A_B; 1GNH, A_B; 1GZX, A_B; 1SWB, A_B; 8TIM, A_B; 3MVO, A_B; 1GZX_dimers, AB_CD; and 1SWB_dimers, AB_CD. The −partners flag was used, meaning that the position of the second chain was perturbed with respect to the stationary first chain. For each of these dockings, 10 000 structures were generated using unrestrained RosettaDock (talaris2014 scoring function). The structures were scored and ranked using the Rosetta protein–protein docking total score as well as the Bayesian scoring function with SID. An application (SID_rescore) was created in Rosetta to rescore poses generated from RosettaDock (see tutorial in the SI).
Safety Statement
No unexpected or unusually high safety hazards were encountered.
Acknowledgments
We thank the members of the Lindert lab for many useful discussions. We would like to thank the Ohio Supercomputer Center for valuable computational resources.102 This work was supported by NIH (P41 GM128577) to S.L. and V.H.W. and R01GM113658 awarded to V.H.W.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00912.
Experimental parameters, tables, figures, and a tutorial (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Yamashita M.; Fenn J. B. Electrospray Ion Source. Another Variation on the Free-Jet Theme. J. Phys. Chem. 1984, 88, 4451–4459. 10.1021/j150664a002. [DOI] [Google Scholar]
- Fenselau C.; Vestling M. M.; Cotter R. J. Mass spectrometric analysis of proteins. Curr. Opin. Biotechnol. 1993, 4, 14–19. 10.1016/0958-1669(93)90026-S. [DOI] [PubMed] [Google Scholar]
- Rostom A. A.; Robinson C. V. Disassembly of intact multi protein complexes in the gas phase. Curr. Opin. Struct. Biol. 1999, 9, 135–141. 10.1016/S0959-440X(99)80018-9. [DOI] [PubMed] [Google Scholar]
- Nettleton E. J.; Tito P.; Sunde M.; Bouchard M.; Dobson C. M.; Robinson C. V. Characterization of the Oligomeric States of Insulin in Self-Assembly and Amyloid Fibril Formation by Mass Spectrometry. Biophys. J. 2000, 79, 1053–1065. 10.1016/S0006-3495(00)76359-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharon M.; Robinson C. V. The Role of Mass Spectrometry in Structure Elucidation of Dynamic Protein Complexes. Annu. Rev. Biochem. 2007, 76, 167–193. 10.1146/annurev.biochem.76.061005.090816. [DOI] [PubMed] [Google Scholar]
- Marcoux J.; Robinson C. V. Twenty Years of Gas Phase Structural Biology. Structure 2013, 21, 1541–1550. 10.1016/j.str.2013.08.002. [DOI] [PubMed] [Google Scholar]
- Lanucara F.; Holman S. W.; Gray C. J.; Eyers C. E. The power of ion mobility-mass spectrometry for structural characterization and the study of conformational dynamics. Nat. Chem. 2014, 6, 281–294. 10.1038/nchem.1889. [DOI] [PubMed] [Google Scholar]
- Allen S. J.; Giles K.; Gilbert T.; Bush M. F. Ion mobility mass spectrometry of peptide, protein, and protein complex ions using a radio-frequency confining drift cell. Analyst 2016, 141, 884–891. 10.1039/C5AN02107C. [DOI] [PubMed] [Google Scholar]
- Lai A. L.; Clerico E. M.; Blackburn M. E.; Patel N. A.; Robinson C. V.; Borbat P. P.; Freed J. H.; Gierasch L. M. Key features of an Hsp70 chaperone allosteric landscape revealed by ion mobility native mass spectrometry and double electron-electron resonance. J. Biol. Chem. 2017, 292, 8773–8785. 10.1074/jbc.M116.770404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eschweiler J. D.; Frank A. T.; Ruotolo B. T. Coming to Grips with Ambiguity: Ion Mobility-Mass Spectrometry for Protein Quaternary Structure Assignment. J. Am. Soc. Mass Spectrom. 2017, 28, 1991–2000. 10.1007/s13361-017-1757-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitner A.; Walzthoeni T.; Kahraman A.; Herzog F.; Rinner O.; Beck M.; Aebersold R. Probing Native Protein Structures by Chemical Cross-linking, Mass Spectrometry, and Bioinformatics. Mol. Cell. Proteomics 2010, 9, 1634–1649. 10.1074/mcp.R000001-MCP201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rappsilber J. The beginning of a beautiful friendship: Cross-linking/mass spectrometry and modelling of proteins and multi-protein complexes. J. Struct. Biol. 2011, 173, 530–540. 10.1016/j.jsb.2010.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinz A. The advancement of chemical cross-linking and mass spectrometry for structural proteomics: from single proteins to protein interaction networks. Expert Rev. Proteomics 2014, 11, 733–743. 10.1586/14789450.2014.960852. [DOI] [PubMed] [Google Scholar]
- Kao A.; Chiu C.-l.; Vellucci D.; Yang Y.; Patel V. R.; Guan S.; Randall A.; Baldi P.; Rychnovsky S. D.; Huang L. Development of a Novel Cross-linking Strategy for Fast and Accurate Identification of Cross-linked Peptides of Protein Complexes. Mol. Cell. Proteomics 2011, 10 (1), 1–17. 10.1074/mcp.M110.002212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendoza V. L.; Vachet R. W. Probing Protein Structure by Amino Acid-Specific Covalent Labeling and Mass Spectrometry. Mass Spectrom. Rev. 2009, 28, 785–815. 10.1002/mas.20203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engen J. R. Analysis of protein complexes with hydrogen exchange and mass spectrometry. Analyst 2003, 128, 623–628. 10.1039/b212800b. [DOI] [PubMed] [Google Scholar]
- Claesen J.; Burzykowski T. Computational Methods and Challenges in Hydrogen/Deuterium Exchange Mass Spectrometry. Mass Spectrom. Rev. 2017, 36, 649–667. 10.1002/mas.21519. [DOI] [PubMed] [Google Scholar]
- Li K. S.; Chen G.; Mo J.; Huang R. R.-C.; Deyanova E. G.; Beno B. R.; O’Niel S. R.; Tymiak A. A.; Gross M. L. Orthogonal Mass Spectrometry-Based Footprinting for Epitope Mapping and Structural Characterization: The IL-6 Receptor upon Binding of Protein Therapeutics. Anal. Chem. 2017, 89, 7742–7749. 10.1021/acs.analchem.7b01748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X.; Grant O. C.; Ito K.; Wallace A.; Wang S.; Zhou P.; Wells L.; Lu S.; Woods R. J.; Sharp J. S. Structural Analysis of the Glycosylated Intact HIV 1 gp120 b12 Antibody Complex Using Hydroxyl Radical Protein Footprinting. Biochem. 2017, 56, 957–970. 10.1021/acs.biochem.6b00888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benesch J. L. P.; Aquilina J. A.; Ruotolo B. T.; Sobott F.; Robinson C. V. Tandem Mass Spectrometry Reveals the Quaternary Organization of Macromolecular Assemblies. Chemistry & Biology 2006, 13, 597–605. 10.1016/j.chembiol.2006.04.006. [DOI] [PubMed] [Google Scholar]
- Beardsley R. L.; Jones C. M.; Galhena E. S.; Wysocki V. H. Non-Covalent Protein Tetramers and Pentamers with “n” Charges Yield Monomers with n/4 and n/5 Charges. Anal. Chem. 2009, 81, 1347–1356. 10.1021/ac801883k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M.; Wysocki V. H. Surface Induced Dissociation: Dissecting Noncovalent Protein Complexes in the Gas phase. Acc. Chem. Res. 2014, 47, 1010–1018. 10.1021/ar400223t. [DOI] [PubMed] [Google Scholar]
- Blackwell A. E.; Dodds E. D.; Bandarian V.; Wysocki V. H. Revealing the Quaternary Structure of a Heterogeneous Noncovalent Protein Complex through Surface-Induced Dissociation. Anal. Chem. 2011, 83, 2862–2865. 10.1021/ac200452b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X.; Zhou M.; Wysocki V. H. Surface Induced Dissociation Yields Quaternary Substructure of Refractory Noncovalent Phosphorylase B and Glutamate Dehydrogenase Complexes. J. Am. Soc. Mass Spectrom. 2014, 25, 368–379. 10.1007/s13361-013-0790-y. [DOI] [PubMed] [Google Scholar]
- Song Y.; Nelp M. T.; Bandarian V.; Wysocki V. H. Refining the Structural Model of a Heterohexameric Protein Complex: Surface Induced Dissociation and Ion Mobility Provide Key Connectivity and Topology Information. ACS Cent. Sci. 2015, 1, 477–487. 10.1021/acscentsci.5b00251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruotolo B. T.; Giles K.; Campuzano I.; Sandercock A. M.; Bateman R. H.; Robinson C. V. Evidence for Macromolecular Protein Rings in the Absence of Bulk Water. Science 2005, 310, 1658–1661. 10.1126/science.1120177. [DOI] [PubMed] [Google Scholar]
- Ruotolo B. T.; Robinson C. V. Aspects of native proteins are retained in vacuum. Curr. Opin. Chem. Biol. 2006, 10, 402–408. 10.1016/j.cbpa.2006.08.020. [DOI] [PubMed] [Google Scholar]
- Popa V.; Trecroce D. A.; McAllister R. G.; Konermann L. Collision-Induced Dissociation of Electrosprayed Protein Complexes: An All-Atom Molecular Dynamics Model with Mobile Protons. J. Phys. Chem. B 2016, 120, 5114–5124. 10.1021/acs.jpcb.6b03035. [DOI] [PubMed] [Google Scholar]
- Song Y.; Nelp M. T.; Bandarian V.; Wysocki V. H. Refining the Structural Model of a Heterohexameric Protein Complex: Surface Induced Dissociation and Ion Mobility Provide Key Connectivity and Topology Information. ACS Cent. Sci. 2015, 1, 447–487. 10.1021/acscentsci.5b00251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall Z.; Hernández H.; Marsh J. A.; Teichmann S. A.; Robinson C. V. The Role of Salt Bridges, Charge Density, and Subunit Flexibility in Determining Disassembly Routes of Protein Complexes. Structure 2013, 21, 1325–1337. 10.1016/j.str.2013.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M.; Huang C.; Wysocki V. H. Surface-Induced Dissociation of Ion Mobility-Separated Noncovalent Complexes in Quadrupole/Time-of-Flight Mass Spectrometer. Anal. Chem. 2012, 84, 6016–6023. 10.1021/ac300810u. [DOI] [PubMed] [Google Scholar]
- Zhou M.; Dagan S.; Wysocki V. H. Protein Subunits Released by Surface Collisions of Noncovalent Complexes: Nativelike Compact Structures Revealed by Ion Mobility Mass Spectrometry. Angew. Chem., Int. Ed. 2012, 51, 4336–4339. 10.1002/anie.201108700. [DOI] [PubMed] [Google Scholar]
- Dodds E. D.; Blackwell A. E.; Jones C. M.; Holso K. L.; E’Brien D. J.; Cordes M. H. J.; Wysocki V. H. Determinants of Gas-Phase Disassembly Behavior in Homodimeric Protein Complexes with Related Yet Divergent Structures. Anal. Chem. 2011, 83, 3881–3889. 10.1021/ac2003906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M.; Jones C. M.; Wysocki V. H. Dissecting the Large Noncovalent Protein Complex GroEL with Surface-Induced Dissociation and Ion Mobility Mass Spectrometry. Anal. Chem. 2013, 85, 8262–8267. 10.1021/ac401497c. [DOI] [PubMed] [Google Scholar]
- Harvey S. R.; Seffernick J. T.; Quintyn R. S.; Song Y.; Ju Y.; Yan J.; Sahasrabuddhe A. N.; Norris A.; Zhou M.; Behrman E. J.; Lindert S.; Wysocki V. H. Relative Interfacial Cleavage Energetics of Protein Complexes Revealed by Surface Collisions. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 8143–8148. 10.1073/pnas.1817632116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y.; Lange O.; Delaglio F.; Rossi P.; Aramini J. M.; Liu G.; Eletsky A.; Wu Y.; Singarapu K. K.; Lemak A.; Ignatchenko A.; Arrowsmith C. H.; Szyperski T.; Montelione G. T.; Baker D.; Bax A. Consistent blind protein structure generation from NMR chemical shift data. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 4685–4690. 10.1073/pnas.0800256105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y.; Vernon R.; Baker D.; Bax A. De novo protein structure generation from incomplete chemical shift assignments. J. Biomol. NMR 2009, 43, 63–78. 10.1007/s10858-008-9288-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vernon R.; Shen Y.; Baker D. Improved chemical shift based fragment selection for CS-Rosetta using Rosetta3 fragment picker. J. Biomol. NMR 2013, 57, 117–127. 10.1007/s10858-013-9772-4. [DOI] [PubMed] [Google Scholar]
- Kontaxis G. An improved algorithm for MFR fragment assembly. J. Biomol. NMR 2012, 53, 149–159. 10.1007/s10858-012-9632-7. [DOI] [PubMed] [Google Scholar]
- Li W.; Zhang Y.; Kihara D.; Huang Y. J.; Zheng D.; Montelione G. T.; Kolinski A.; Skolnick J. TOUCHSTONEX: Protein Structure Prediction With Sparse NMR Data. Proteins: Struct., Funct., Genet. 2003, 53, 290–306. 10.1002/prot.10499. [DOI] [PubMed] [Google Scholar]
- Hirst S. J.; Alexander N.; Mchaorab H. S.; Meiler J. RosettaEPR: An integrated tool for protein structure determination from sparse EPR data. J. Struct. Biol. 2011, 173, 506–514. 10.1016/j.jsb.2010.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer A. W.; Bordigton E.; Bleicken S.; García-Sáez A. J.; Jeschke G.; Meiler J. Pushing the size limit of de novo structure ensemble prediction guided by sparse SDSL-EPR restraints to 200 residues: The monomeric and homodimeric forms of BAX. J. Struct. Biol. 2016, 195, 62–71. 10.1016/j.jsb.2016.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer A. W.; Alexander N. S.; Woetzel N.; Karakas M.; Weiner B. E.; Meiler J. BCL::MP-fold: Membrane protein structure prediction guided by EPR restraints. Proteins: Struct., Funct., Genet. 2015, 83, 1947–1962. 10.1002/prot.24801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R.; André I.; Shen Y.; Wu Y.; Lemak A.; Bansal S.; Arrowsmith C. H.; Szyperski T.; Baker D. Simultaneous prediction of protein folding and docking at high resolution. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 18978–18983. 10.1073/pnas.0904407106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman-Duhovny D.; Hammel M.; Tainer J. A.; Sali A. FoXS, FoXSDock and MultiFoXS: Single-state and multi state structural modeling of proteins and their complexes based on SAXS profiles. Nucleic Acids Res. 2016, 10, W424–W429. 10.1093/nar/gkw389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karczyńska A. S.; Mozolewska M. A.; Krupa P.; Giełdón A.; Liwo A.; Czaplewski C. Prediction of protein structure with the coarse-grained UNRES force field assisted by small X-ray scattering data and knowledge-based information. Proteins 2017, 86 (S1), 228–239. 10.1002/prot.25421. [DOI] [PubMed] [Google Scholar]
- Lindert S.; Alexander N.; Wotzel N.; Karakas M.; Stewart P. L.; Meiler J. EM-Fold: De Novo Atomic-Detail Protein Structure Determination from Medium-Resolution Density Maps. Structure 2012, 20, 464–478. 10.1016/j.str.2012.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindert S.; Hofmann T.; Wötzel N.; Karakas M.; Stewart P. L.; Meiler J. Ab initio protein modeling into cryoEM density maps using EM-Fold. Biopolymers 2012, 97, 669–677. 10.1002/bip.22027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindert S.; Staritzbichler R.; Wötzel N.; Karakas M.; Stewart P. L.; Meiler J. EM-Fold: De novo Folding of α -helical Proteins Guided by Intermediate Resolution Electron Microscopy Density Maps. Structure 2009, 17, 990–1003. 10.1016/j.str.2009.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frenz B.; Walls A. C.; Edelman E. H.; Veesler D.; DiMaio F. RosettaES: a sampling strategy enabling automated interpretation of difficult cryo-EM maps. Nat. Methods 2017, 14, 797–800. 10.1038/nmeth.4340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiMaio F.; Song Y.; Li X.; Brunner M. J.; Xu C.; Conticello V.; Engelman E.; Marlovitis T.; Cheng Y.; Baker D. Atomic accuracy models from 4.5 Å cryo-electron microscopy data with density-guided iterative local refinement. Nat. Methods 2015, 12, 361–365. 10.1038/nmeth.3286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiMaio F.; Tyka M. D.; Baker M. L.; Chiu W.; Baker D. Refinement of Protein Structures into Low-Resolution Density Maps using Rosetta. J. Mol. Biol. 2009, 392, 181–190. 10.1016/j.jmb.2009.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singharoy A.; Teo I.; McGreevy R.; Stone J. E.; Jianhua Z.; Schulten K. Molecular dynamics-based refinement and validation for a sub-5 Å cryo-electron microscopy maps. ELife 2016, 5, 1–32. 10.7554/eLife.16105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trabuco L. G.; Schreiner E.; Gumbart J.; Hsin J.; Villa E.; Schulten K. Applications of the molecular dynamics flexible fitting method. J. Struct. Biol. 2011, 173, 420–427. 10.1016/j.jsb.2010.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trabuco L. G.; Villa E.; Mitra K.; Frank J.; Schulten K. Flexible Fitting of Atomic Structures into Electron Microscopy Maps Using Molecular Dynamics. Structure 2008, 16, 673–683. 10.1016/j.str.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindert S.; McCammon J. A. Improved cryoEM-Guided Iterative Molecular Dynamics - Rosetta Protein Structure Re fi nement Protocol for High Precision Protein Structure Prediction. J. Chem. Theory Comput. 2015, 11, 1337–1346. 10.1021/ct500995d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindert S.; Meiler J.; McCammon J. A. Iterative Molecular Dynamics -- Rosetta Protein Structure Refinement Protocol to Improve Model Quality. J. Chem. Theory Comput. 2013, 9, 3843–3847. 10.1021/ct400260c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leelananda S. P.; Lindert S. Iterative Molecular Dynamics - Rosetta Membrane Protein Structure Refinement Guided by Cryo-EM Densities. J. Chem. Theory Comput. 2017, 13, 5131–5145. 10.1021/acs.jctc.7b00464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M.; Baldwin P. R.; Ludtke S. J.; Baker M. L. De Novo modeling in cryo-em density maps with Pathwalking. J. Struct. Biol. 2016, 196, 289–298. 10.1016/j.jsb.2016.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts V. A.; Thompson E. E.; Pique M. E.; Perez M. S.; Eyck L. T. DOT2: Macromolecular Docking With Improved Biophysical Models. J. Comput. Chem. 2013, 34, 1743–1758. 10.1002/jcc.23304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastritis P. L.; Rodrigues J. P. G. L. M.; Bonvin A. M. J. J. HADDOCK 2P2I: A Biophysical Model for Predicting the Binding A ffi nity of Protein - Protein Interaction Inhibitors. J. Chem. Inf. Model. 2014, 54, 826–836. 10.1021/ci4005332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce B. G.; Wiehe K.; Hwang H.; Kim B.-H.; Vreven T.; Weng Z. ZDOCK server: interactive docking prediction of protein-protein complexes and symmetric multimers. Bioinformatics 2014, 30, 1771–1773. 10.1093/bioinformatics/btu097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeau S. R.; Gatchell D. W.; Vajda S.; Camacho C. J. ClusPro: an automated docking and discrimination method for the prediction of protein complexes. Bioinformatics 2004, 20, 45–50. 10.1093/bioinformatics/btg371. [DOI] [PubMed] [Google Scholar]
- Kozakov D.; Hall D. R.; Xia B.; Porter K. A.; Padhorny D.; Yueh C.; Beglov D.; Vajda S. The ClusPro web server for protein-protein docking. Nat. Protoc. 2017, 12, 255–278. 10.1038/nprot.2016.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S. S.; Seffernick J. T.; Lindert S. Accurately Predicting Disordered Regions of Proteins Using Rosetta ResidueDisorder Application. J. Phys. Chem. B 2018, 122, 3920–3930. 10.1021/acs.jpcb.8b01763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman-Duhovny D.; Inbar Y.; Nussinov R.; Wolfson H. J. PatchDock and SymmDock: servers for rigid and symmetric docking. Nucleic Acids Res. 2005, 33, W363–W367. 10.1093/nar/gki481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray J. J.; Moughon S.; Wang C.; Schueler-Furman O.; Kuhlman B.; Rohl C. A.; Baker D. Protein-Protein Docking with Simultaneous Optimization of Ridig-body Displacement and Side-chain Conformations. J. Mol. Biol. 2003, 331, 281–299. 10.1016/S0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- Alford R. F.; Leaver-Fay A.; Jeliazkov J. R.; O’Meara M. J.; Di Maio F. P.; Park H.; Shapovalov M. V.; Renfrew P. D.; Mulligan V. K.; Kappel K.; Labonte J. W.; Pacella M. S.; Bonneau R.; Bradley P.; Dunbrack R. L. Jr.; Das R.; Baker D.; Kuhlman B.; Kortemme T.; Gray J. J. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J. Chem. Theory Comput. 2017, 13, 3031–3048. 10.1021/acs.jctc.7b00125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Schueler-Furman O.; Baker D. Improved side-chain modeling for protein-protein docking. Protein Sci. 2005, 14, 1328–1339. 10.1110/ps.041222905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Bradley P.; Baker D. Protein-Protein Docking with Backbone Flexibility. J. Mol. Biol. 2007, 373, 503–519. 10.1016/j.jmb.2007.07.050. [DOI] [PubMed] [Google Scholar]
- Chaudhury S.; Berrondo M.; Weitzner B. D.; Muthu P.; Bergman H.; Gray J. J. Benchmarking and Analysis of Protein Docking Performance in Rosetta v3.2. PLoS One 2011, 6, e22477. 10.1371/journal.pone.0022477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilambi K. P.; Reddy K.; Gray J. J. Protein-Protein Docking with Dynamic Residue Protonation States. PLOS Comput. Biol. 2014, 10, e1004018. 10.1371/journal.pcbi.1004018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marze N. A.; Jeliazkov J. R.; Burman S. S. R.; Boyken S. E.; Dimaio F.; Gray J. J. Modeling oblong proteins and water-mediated interfaces with RosettaDock in CAPRI rounds 28–35. Proteins 2017, 85, 479–486. 10.1002/prot.25168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahraman A.; Herzog F.; Leitner A.; Rosenberger G.; Aebersold R.; Malmström L. Cross-Link Guided Molecular Modeling with ROSETTA. PLoS One 2013, 8, e73411. 10.1371/journal.pone.0073411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aprahamian M. H.; Chea E. E.; Jones L. M.; Lindert S. Rosetta Protein Structure Prediction from Hydroxyl Radical Protein Footprinting Mass Spectrometry Data. Anal. Chem. 2018, 90, 7721–7729. 10.1021/acs.analchem.8b01624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russel D.; Lasker K.; Webb B.; Velazquez-Muriel J.; Tjioe E.; Schneidman-Duhovny D.; Peterson B.; Sali A. Putting the Pieces Together: Integrative Modeling Platform Software for Structure Determination of Macromolecular Assemblies. PLOS. Biol. 2012, 10, e1001244. 10.1371/journal.pbio.1001244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webb B.; Viswanath S.; Bonomi M.; Pellarin R.; Greenberg C. H.; Saltzberg D.; Sali A. Integrative structure modeling with the Integrative Modeling Platform. Protein Sci. 2018, 27, 245–258. 10.1002/pro.3311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Politis A.; Schmidt C. Structural characterisation of medically relevant protein assemblies by integrating mass spectrometry with computational modelling. J. Proteom 2018, 175, 34. 10.1016/j.jprot.2017.04.019. [DOI] [PubMed] [Google Scholar]
- Politis A.; Park A. Y.; Hall Z.; Ruotolo B. T.; Rovbinson C. V. Integrative Modelling Coupled with Ion Mobility Mass Spectrometry Reveals Structural Features of the Clamp Loader in Complex with Single Stranded DNA Binding Protein. J. Mol. Biol. 2013, 425, 4790–4801. 10.1016/j.jmb.2013.04.006. [DOI] [PubMed] [Google Scholar]
- Molnar K. S.; Bonomi M.; Pellarin R.; Clinthorne G. D.; Gonzalez G.; Goldberg S. D.; Goulian M.; Sali A.; DeGrado W. F. Cys-Scanning Disulfide Crosslinking and Bayesian Modeling Probe the Transmembrane Signaling Mechanism of the Histidine Kinase, PhoQ. Structure 2014, 22, 1239–1251. 10.1016/j.str.2014.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng-Elmore X.; Gao X.-Z.; Pellarin R.; Schneidman-Duhovy D.; Zhang X.-J.; Kozacka K. A.; Tang Y.; Sali A.; Chalkey R. J.; Cote R. H.; Chu F. Molecular Architecture of Photoreceptor Phosphodiesterase Elucidated by Chemical Cross-Linking and Integrative Modeling. J. Mol. Biol. 2014, 426, 3713–3728. 10.1016/j.jmb.2014.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y.; Fernandez-Martinez J.; Tjioe E.; Pellarin R.; Kim S. J.; Williams R.; Schneidman-Duhovy D.; Sali A.; Rout M. P.; Chait B. T. Structural Characterization by Cross-linking Reveals the Detailed Architecture of a Coatomer-related Heptameric Module from the Nuclear Pore Complex. Mol. Cell. Peoteomics 2014, 13 (11), 2927–2943. 10.1074/mcp.M114.041673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z. A.; Pellarin R.; Fischer L.; Sali A.; Nilges M.; Barlow P. N.; Rappsilber J. Structure of Complement C3(H 2 O) Revealed By Quantitative Cross-Linking/Mass Spectrometry And Modeling. Mol. Cell. Proteomics 2016, 15 (8), 2730–2743. 10.1074/mcp.M115.056473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg C. H.; Kollman J.; Zelter A.; Johnson R.; MacCoss M. J.; Davis T. N.; Agard D. A.; Sali A. Structure of γ -tubulin small complex based on a cryo-EM map, chemical cross-links, and a remotely related structure. J. Struct. Biol. 2016, 194, 303–310. 10.1016/j.jsb.2016.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall Z.; Schmidt C.; Politis A. Uncovering the Early Assembly Mechanism for Amyloidogenic β 2 -Microglobulin Using Cross-linking and Native Mass Spectrometry. J. Biol. Chem. 2016, 291, 4626–4637. 10.1074/jbc.M115.691063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasker K.; Forster F.; Bohn S.; Walzthoeni T.; Villa E.; Unverdorben P.; Beck F.; Aebersold R.; Sali A.; Baumeister W. Molecular architecture of the 26S proteasome holocomplex determined by an integrative approach. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 1380–1387. 10.1073/pnas.1120559109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt C.; Macpherson J. A.; Lau K. W.; Fraternali F.; Politis A. Surface Accessibility and Dynamics of Macromolecular Assemblies Probed by Covalent Labeling Mass Spectrometry and Integrative Modeling. Anal. Chem. 2017, 89, 1459–1468. 10.1021/acs.analchem.6b02875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweppe D. K.; Zheng C.; Chavez J. D.; Navare A. T.; Eng J. K.; Bruce J. E. XLinkDB 2.0: integrated, large-scale structural analysis of protein crosslinking data. Bioinformatics 2016, 32, 2716–2718. 10.1093/bioinformatics/btw232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosinski J.; von Appen A.; Ori A.; Karius K.; Müller C. W.; Beck M. Xlink Analyzer: Software for analysis and visualization of cross-linking data in the context of three-dimensional structures. J. Struct. Biol. 2015, 189, 177–183. 10.1016/j.jsb.2015.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferber M.; Kosinski J.; Ori A.; Rashid U. J; Moreno-Morcillo M.; Simon B.; Bouvier G.; Batista P. R.; Muller C. W; Beck M.; Nilges M. Automated structure modeling of large protein assemblies using crosslinks as distance restraints. Nat. Methods 2016, 13, 515–520. 10.1038/nmeth.3838. [DOI] [PubMed] [Google Scholar]
- Gong Z.; Liu Z.; Dong X.; Ding Y.-H.; Dong M.-Q.; Tang C. Protocol for analyzing protein ensemble structures from chemical cross-links using DynaXL. Biophys. Rep. 2017, 3, 100–108. 10.1007/s41048-017-0044-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trahan C.; Oeffinger M. Targeted cross-linking-mass spectrometry determines vicinal interactomes within heterogeneous RNP complexes. Nucleic Acids Res. 2016, 44, 1354–1369. 10.1093/nar/gkv1366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts V. A.; Pique M. E.; Hsu S.; Li S. Combining H/D Exchange Mass Spectrometry and Computational Docking To Derive the Structure of Protein-Protein Complexes. Biochemistry 2017, 56, 6329–6342. 10.1021/acs.biochem.7b00643. [DOI] [PubMed] [Google Scholar]
- Hall Z.; Politis A.; Bush M. F.; Smith L. J.; Robinson C. V. Charge-State Dependent Compaction and Dissociation of Protein Complexes: Insights from Ion Mobility and Molecular Dynamics. J. Am. Chem. Soc. 2012, 134, 3429–3438. 10.1021/ja2096859. [DOI] [PubMed] [Google Scholar]
- Pagel K.; Hyung S.-J.; Ruotolo B. T.; Robinson C. V. Alternate Dissociation Pathways Identified in Charge-Reduced Protein Complex Ions. Anal. Chem. 2010, 82, 5363–5372. 10.1021/ac101121r. [DOI] [PubMed] [Google Scholar]
- Zhou M.; Dagan S.; Wysocki V. H. Impact of charge state on gas-phase behaviors of noncovalent protein complexes in collision induced dissociation and surface induced dissociation. Analyst 2013, 138, 1353–1362. 10.1039/c2an36525a. [DOI] [PubMed] [Google Scholar]
- Quintyn R. S.; Zhou M.; Yan J.; Wysocki V. H. Surface-induced dissociation mass spectra as a tool for distinguishing different structural forms of gas-phase multimeric protein complexes. Anal. Chem. 2015, 87, 11879–11886. 10.1021/acs.analchem.5b03441. [DOI] [PubMed] [Google Scholar]
- Kryshtafovych A.; Venclovas Č.; Fidelis K.; Moult J. Progress Over the First Decade of CASP Experiments. Proteins 2005, 61, 225–236. 10.1002/prot.20740. [DOI] [PubMed] [Google Scholar]
- Bhardwaj G.; Mulligan V. K.; Bahl C. D.; Gilmore J. M.; Harvey P. J.; Cheneval O.; Buchko G. W.; Pulavarti S. V. S. R. K.; Eletsky A.; Huang P.-S.; Johnson W. A.; Greisen P. J.; Rocklin G. J.; Song Y.; Linsky T. W.; Watkins A.; Rettie S. A.; Xu X.; Carter L. P.; Bonneau R.; Olson J. M.; Coutsias E.; Correnti C. E.; Szyperski T.; Craik D. J.; Baker D. Accurate de novo design of hyperstable constrained peptides. Nature 2016, 538, 329–335. 10.1038/nature19791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis S. M.; Kuhlman B. A. Anchored Design of Protein-Protein Interafaces. PLoS One 2011, 6, e20872. 10.1371/journal.pone.0020872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiusalaas J.Numerical Methods in Engineering with Python 3; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ohio Supercomputer Center. Ohio Supercomputer Center: Columbus, OH, 1987; http://osc.edu/ark:/19495/f5s1ph73.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.