Tuning the Electric Field Response of MOFs by Rotatable Dipolar Linkers

Abstract

Recently the possibility of using electric fields as a further stimulus to trigger structural changes in metal–organic frameworks (MOFs) has been investigated. In general, rotatable groups or other types of mechanical motion can be driven by electric fields. In this study we demonstrate how the electric response of MOFs can be tuned by adding rotatable dipolar linkers, generating a material that exhibits paraelectric behavior in two dimensions and dielectric behavior in one dimension. The suitability of four different methods to compute the relative permittivity κ by means of molecular dynamics simulations was validated. The dependency of the permittivity on temperature T and dipole strength μ was determined. It was found that the herein investigated systems exhibit a high degree of tunability and substantially larger dielectric constants as expected for MOFs in general. The temperature dependency of κ obeys the Curie–Weiss law. In addition, the influence of dipolar linkers on the electric field induced breathing behavior was investigated. With increasing dipole moment, lower field strengths are required to trigger the contraction. These investigations set the stage for an application of such systems as dielectric sensors, order–disorder ferroelectrics, or any scenario where movable dipolar fragments respond to external electric fields.

Short abstract

Rotatable dipolar groups, used as organic linkers in metal−organic frameworks (MOFs), can substantially alter their electric field response, in terms of both their dielectric and flexible properties.

Introduction

Metal–organic frameworks (MOFs) are an emerging class of crystalline, hybrid, and porous materials, which are built from oligotopic molecules (linkers) and metal ion nodes.¹⁻³ Potential applications for MOFs are gas separation and storage, water purification, chemical sensing, catalysis, drug delivery, and imaging.⁴⁻⁸ In particular, so-called stimuli-responsive MOFs, which undergo physical or chemical “changes of large amplitude in response to external stimulation”,⁹ have gained much attention for the design of new functional materials.^10,11 Well-studied external stimuli are temperature, mechanical pressure, guest adsorption or evacuation, and light absorption.

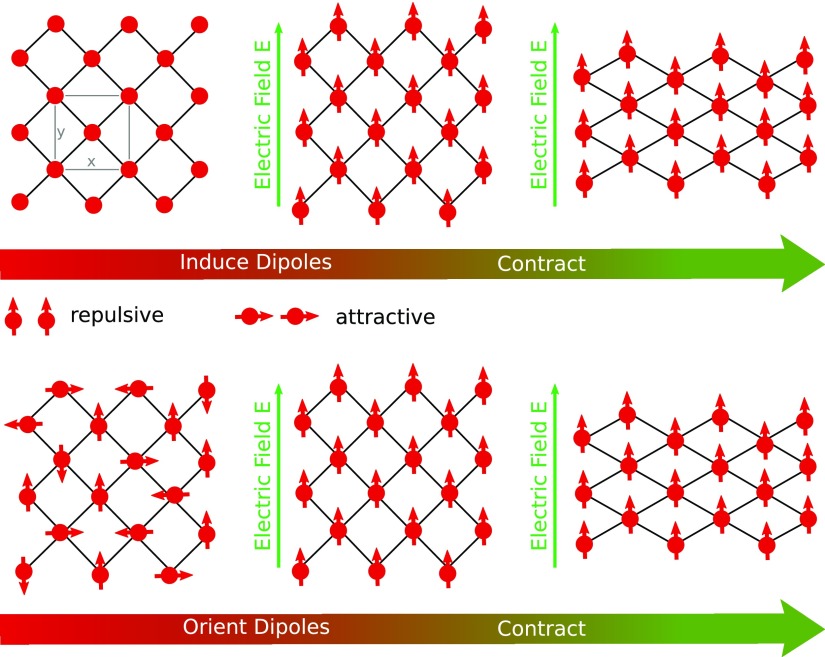
Recently, the possibility to use external electric fields E as a further stimulus to trigger structural changes in MOFs has been reported. By molecular dynamics simulations, the well-known breathing behavior of MIL-53(Cr) could be reproduced, however, only by applying a very high external electric field.¹² One of us proposed a potential mechanism for this transformation, based on field-induced dipole–dipole interactions in a wine-rack-type lattice (see Figure 6).¹³ Recently, Kolesnikov and co-workers confirmed this mechanism for a 2D lattice model by statistical mechanics calculations.¹⁴ Furthermore, Knebel et al. demonstrated that an electric field can be used to enhance the molecular sieving capability of a ZIF-8-based MOF-polymer membrane by initiating reversible phase transitions.¹⁵

Figure 6.

Upper panel: 2D lattice of induced (aligned) dipoles. The gray box in the left figure indicates our choice of the unit cell, which is rotated by 90° in respect to the conventional one (size in respect to the conventional is 2 × 1 × 1). Lower panel: 2D lattice of permanent dipoles. The dipole–dipole interaction is stabilized undergoing the large pore–small pore phase transition.

On the other hand, in addition to guest adsorption, the regularity and porosity of MOFs make them an ideal platform to realize molecular machines. The void space allows for the motion of either the MOF building blocks, such as rotating linkers,¹⁶ or molecular guests inside the pores. For example, Loeb and co-workers incorporated a rotaxane moiety in the linker of an MOF.¹⁷ Very recently, the unidirectional rotation of a light-driven rotor within an MOF was demonstrated.¹⁸ Again, external electric fields are a facile way to trigger motion of movable components in MOFs. For example, Yazaydin and co-workers investigated two interesting systems in silico, where the transport of guests is modulated by the help of dipolar groups ordering in an external electric field. In the first case, a large dipolar molecule was mounted on the open metal coordination sites in Mg-MOF-74, which acts as a molecular gate, controlling the flow of guest molecules along the hexagonal channels.¹⁹ In the second example, the guest diffusion in an IRMOF variant with a dipolar group at the linker was modulated by applying an external field.²⁰ Due to the ordering of linkers in the field, a nonisotropic self-diffusion was observed.

To gain a deeper understanding of any kind of field induced motion or structural transformation in a system, its dielectric permittivity κ needs to be known. However, due to the general interest in electrically insulating MOFs as potential low-κ interlayer dielectrics for semiconducting devices, past theoretical investigations were mainly focusing on the electronic polarization of rigid MOFs in the linear response regime. Note that a somewhat related current development is, on the other hand, electrically conducting MOFs, which respond by a current on an electric field.²¹ Nevertheless, in the context of MOFs as low-κ materials at first Zagorodniy et al. studied the dielectric response of cubic Zn-based frameworks, employing the semiempirical Clausius–Mossotti model.²² Later, Warmbier et al. employed density functional perturbation theory to calculate κ for similar rigid cubic frameworks.²³ Inspired by these theoretical studies, the dielectric and optical properties of HKUST-1²⁴ and ZIF-8²⁵ were investigated experimentally, confirming that MOFs are indeed promising candidates for low-κ dielectrics.²⁶ Recent theoretical investigations by Ryder and co-workers, again based on static density functional theory (DFT) calculations, established structure–property relations for the dielectric response of MOFs.^27,28 They found only a minor dependency of κ on the chemical composition of the MOF but an almost linear dependency on the porosity.

The dielectric properties of MOFs with incorporated dipolar rotors have, on the other hand, not been investigated up to now. In contrast to the systems studied by Ryder et al., a strong dependency of κ on the chemical composition, and in particular on the dipole strength of the rotor, is expected, since the highly temperature-dependent orientation polarization should dominate over the electronic polarization in these systems. As a consequence, molecular dynamics (MD) simulations at finite temperature are needed for the determination of the static dielectric permittivity κ. In this work we used pillared layer MOFs as reference systems to establish the methodology, and to investigate the influence of increasing dipole strength and temperature on the dielectric constant for a given framework structure. In our reference systems, square lattices of 1,4-benzenedicarboxylate (bdc) linked zinc paddle-wheels are pillared by bispyridine linkers as shown in Figure 1. The parent system (A) with a central phenyl exhibits no dipolar group. In B 1,2-difluorophenyl and in C phtalazine replace the phenyl in the backbone with an increasing dipole strength. This setup allows for an easy manipulation of the dielectric response of the material, by keeping its other properties unaffected. Furthermore, this system is realistic and could even be deposited as a thin film on a device by layer-by-layer synthesis.²⁹

Figure 1.

Investigated systems with zinc paddle-wheels as inorganic building blocks, which are connected in the pcu topology by phenyl moieties (blue) in the x- and y-direction and pillared in the z-direction by bispyridine units (red). Between the two pyridine units, different organic moieties (A–C) can be mounted to vary the dipole moment of the pillar linker.

For the determination of κ we followed the work by Zhang and Sprik who proposed four different methods to calculate κ from classical MD simulations in the case of liquid water (namely, from polarization fluctuations or as a finite field derivative with either fixed electric field E or fixed displacement charge field D).³⁰ In contrast to the molecular liquid water, the herein investigated systems are porous crystalline polymers and show a nonisotropic dielectric response, since the dipolar linkers can only rotate around the z-axis. Furthermore, the dipole density is much lower and thus also the possible polarization. To determine the numerically most efficient way of predicting κ for such systems, the four proposed methods were applied to systems B and C, and its performance was validated. In addition, we verified the hypothesis that dipolar groups facilitate the electric field induced breathing¹³ which was observed originally for MIL-53.

Methods

Dielectric Constants from MD Simulations

When a material is exposed to an electric field, it becomes polarized. The induced polarization P is related to the electric field E by the electric susceptibility χ

1

The relative permittivity of a material (i.e., its dielectric constant) κ is then given by κ = 1 + χ. In general, this relative permittivity is not a constant but depends on the frequency of the applied field, the temperature T, and other parameters. The induced polarization can be divided into three different contributions: electronic P_el, displacive (ionic) P_ion, and orientation polarization P_orient. Consequently, the relative permittivity can be written as κ = 1 + χ_el + χ_ion + χ_orient. P_el corresponds to the response of the electron density to the electric field. At the high-frequency limit this contribution is crucial, since the nuclei move too slowly to adapt. The ionic polarization is due to the adaptation of the nuclei positions with respect to the electric field. Orientation polarization arises whenever molecules or molecular groups carry a permanent dipole moment μ, which becomes partially aligned to the electric field. For polar liquids this third contribution becomes dominating.

In their investigation on liquid water, Zhang and Sprik proposed four different methods to calculate relative permittivities from classical molecular dynamics simulations, based on two different Hamiltonians.³⁰ In the constant-E method, the electric enthalpy of a system of volume Ω is written as

2

where H_PBC is a classical Hamiltonian with v denoting the set of momenta and positions of the atoms, E is the fixed electric field, and P(v) is the macroscopic polarization for the microscopic state specified by v. Note that the SI unit system is used in this work throughout (conversion formulas to the CGS unit system are given in the SI). Thus, the field-dependent force on atom i is q_iE, where q_i is the charge assigned to the atom in the FF model.

In the constant-D method, the electric internal energy 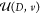functional is written as

3

where D denotes the fixed macroscopic electric displacement field and ϵ₀ the vacuum permittivity.³¹ From this follows that the field-dependent force on atom i is . In contrast to MD simulations using the fixed-E approach, here, the instantaneous polarization P has to be known at every time step, because the force depends explicitly on its value. Since P is a multivalued property and depends on the choice of the unit cell,³² it has to be assured that all atoms are kept in the same reference frame during the simulation. Furthermore, because MOFs are crystalline periodic materials, it is practically impossible to define a unit cell with a vanishing dipole moment and thus a polarization of zero. Therefore, prerequisite to a simulation with a fixed-D Hamiltonian, a corresponding simulation with E = 0 has to be performed to sample the polarization at zero field for the unit cell of choice, which is then used as reference polarization in eq 3. In general, as discussed already by Stengel et al., the constant-E Hamiltonian corresponds macroscopically to a capacitor in short circuit, since polarization fluctuations have to be compensated by fluctuating charges on the capacitor plates. In contrast, the constant-D Hamiltonian is related to a capacitor in open-circuit conditions with a fixed value of free charge Q on the plates, with the polarization fluctuations leading to a fluctuating field E.^30,31

Relative permittivities κ can now be derived from polarization fluctuations at either E = 0 (using the fixed-E Hamiltonian from eq 2) or D = 0 (using the fixed-D Hamiltonian from eq 3). With E = 0, κ can be derived from the fluctuations of the polarization P by

4

where k_B is Boltzmann’s constant, and T is the temperature. Note that due to the anisotropy of the investigated systems we do not average over spatial directions. The brackets ⟨·⟩ denote here the usual ensemble averages. For D = 0, κ is calculated from

5

Furthermore, relative permittivities can also be estimated from simulations for a finite field by extrapolating then to the limit of zero field. For an electric field E, κ can be computed by using the relation

6

with ⟨P_x⟩ the expectation value of the polarization obtained from an MD run using the constant E_x = E Hamiltonian. The finite D derived value for κ follows from the relation

7

where the expectation value of the polarization is determined from an average over a trajectory generated by the constant D_x = D Hamiltonian. Note that, for both approaches, ⟨P_x⟩ is obtained in relation to the average polarization from a trajectory at E = 0, with the same choice for the unit cell.

Computational Details

All molecular dynamics simulations were performed using the MOF-FF force-field^33,34 (parameter sets are provided in the SI), employing our in-house developed PYDLPOLY code.³³ The Ewald summation method was used for calculating the electrostatic interactions, and the short-range interactions were truncated smoothly at 12 Å. The unit cells for the materials were chosen as shown in Figure 6 by a rotation of 45° around the crystallographic c-axis of the conventional cell, which results in a unit cell 2 times larger than the conventional one. Simulations in the (N, V, T) ensemble for the calculations of the dielectric constants were performed in a 2 × 2 × 2 supercell of the rotated unit cell at temperatures of 150, 298, and 450 K. For every system and applied field strength the material was first equilibrated for 100 ps using a Berendsen thermostat³⁵ with a time constant of 200 fs and then further simulated for at least 10 ns using a Nosé–Hoover thermostat³⁶ with a time constant of 1 ps. For all simulations a time step of 1 fs was used. The polarization was monitored every 10th time step. Statistical errors of the polarization P were calculated by performing a reblocking analysis.³⁷

For the investigation of the electric field induced breathing behavior, we always employed a larger 6 × 2 × 2 supercell of the rotated unit cell at 298 K and a pressure of 1 bar. At every field strength the system was first equilibrated for 50 ps in the (N, V, T) ensemble using a Berendsen thermostat³⁵ with a time constant of 200 fs. Then, it was equilibrated in the (N, σ, T) ensemble for 2 ns by a Berendsen thermostat (time constant of 200 fs) and barostat (time constant of 1 ps) followed by a sampling run of 5 ns using a Nosé–Hoover thermostat (time constant of 1 ps) and barostat (time constant of 1 ps).

Results and Discussion

Dielectric Constants

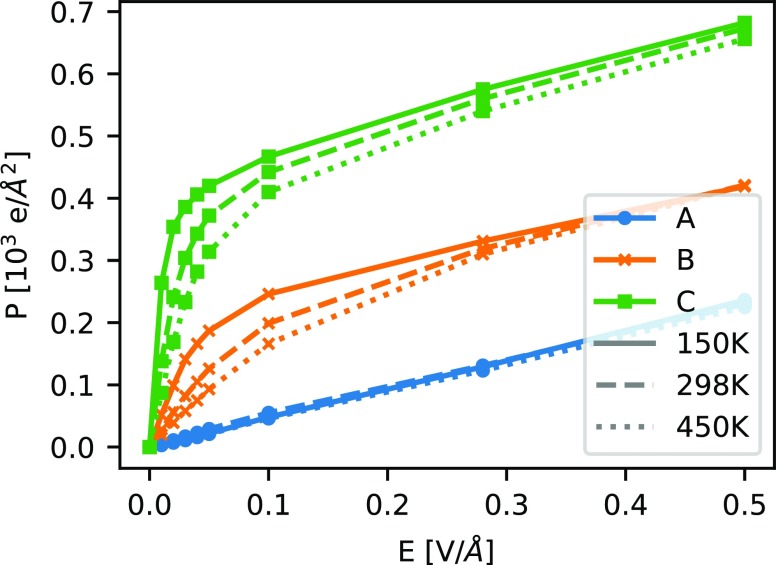
The polarization response P_x for a finite electric field E_x, applied in the x-direction, is shown in Figure 2 for all three MOF systems (Figure 1) at temperatures T of 150, 298, and 450 K. As expected, system A behaves substantially different from systems B and C. Whereas A shows the typical behavior of a dielectric material, i.e., the polarization P increases as a linear function of the electric field E, systems B and C show a nonlinear response, typical for paraelectric materials. The difference is due to the fact that systems B and C carry rotatable dipolar groups. Thus, the first, relatively steep increase of the polarization P with increasing electric field E corresponds to orientation polarization from an alignment of the dipolar groups. The second, flatter part of the curve corresponds to an increasing ionic polarization, as also observed for system A. With increasing dipole moment of the linker groups, the polarization increases substantially for a given field. In addition, in contrast to A, the polarization for B and C becomes highly temperature-dependent, since the field alignment is hampered by the entropy of the dipolar rotors. It should be noted that, due to the anisotropy of the systems, the same behavior is observed for a field applied in the y-direction, whereas for a field applied in the z-direction, only a dielectric response (as for system A) is observed also for B and C, since the dipolar rotors can only rotate about the z-axis. Note that this rotation is almost barrier-free. During the force-field validation we determined a rotational barrier around the Zn–N bond of only 0.15 kcal mol^–1 by DFT calculations of nonperiodic model systems.

Figure 2.

Polarization P_x as a function of the applied electric field E_x for all investigated systems at temperatures of 150 K (blue), 298 K (orange), and 450 K (red).

Due to the use of a nonpolarizable force-field, only ionic and orientation polarization are taken into account when the relative permittivities κ are predicted in the following. However, the additional electronic contribution can be estimated by the structure–property relations developed recently by Ryder et al.²⁸ They found an almost linear dependency between porosity and relative permittivity for a variety of MOFs. Using Zeo++,³⁸ a porosity of about 50% was calculated for all systems. This corresponds to a κ ≈ 1.8 or χ ≈ 0.8, which needs to be added to the here predicted permittivities for a comparison with experimental values. However, since we are mainly interested in relative values, we report in the following on the uncorrected numbers.

In the first step, dielectric constants were calculated on the basis of polarization fluctuations obtained from simulations at E = 0 (see eq 4) and D = 0 (see eq 5). Fluctuations were sampled for every system and temperature for 50 ns. The mean of the polarization obtained from the E = 0 simulation was used as reference polarization for the D = 0 case. The results are shown in Table 1. κ is calculated as average over κ_x and κ_y, since the system is isotropic in the x- and y-direction. This is demonstrated in Figure 3, where the convergence of the variance s² = ⟨P²⟩ – ⟨P⟩² over the time of the MD simulation is shown for system B for E = 0 and D = 0 at 450 K. Both approaches yield the same result in κ, which proves that our treatment of the multivalued polarization³² by making use of the reference polarization in the case of constant D simulations is indeed correct. In accordance to the observations by Zhang and Sprik, the polarization fluctuations are lower for D = 0, and σ² converges faster in comparison to E = 0 simulations (see Figure 3). Despite that, it has to be taken into account that, prerequisite to a constant-D simulation, a constant-E simulation needs to be performed to determine the reference polarization. Note that this is not necessary for a molecular dipolar fluid like water but inevitable for a periodic crystalline polymer like an MOF. As a consequence, the constant-D approach is computationally more demanding and also more sensitive to systematic errors due to potentially insufficient sampling of the reference polarization.

Table 1. Dielectric Constants κ Obtained from Polarization Fluctuations^a.

	T = 150 K		T = 298 K		T = 450 K
	E = 0	D = 0	E = 0	D = 0	E = 0	D = 0
system B	2.01(7)	2.1(1)	1.52(1)	1.53(1)	1.357(5)	1.362(6)
system C	6.8(3)	6.8(7)	3.65(8)	4.0(2)	2.65(4)	2.85(8)

^aTo give an impression for the sampling error, ±2σ is given as statistical error.

Figure 3.

Accumulating variance s² of the total polarization P in x- and y-directions for system B at 450 K for (a) E = 0 and (b) D = 0.

Next, we tested the suitability of the proposed approaches to calculate κ as finite field derivative from simulations with an applied E or D field for our case of an MOF with dipolar rotors. Constant-E_x simulations were performed at different field strengths ranging from 0.005 to 0.50 V Å^–1, sampling the polarization each time for 10 ns. As a consistency check we selected nine values for E_x (see the first column of Table 2) for the case of system C at 150 K and calculated the polarization P_x. The relationship D = ϵ₀E + P was employed to obtain the corresponding D values. These values were then taken as the displacement field in constant-D_x simulations using the Hamiltonian of eq 3. The excellent correspondence in the resulting P_x as obtained by the two different methods underlines again the suitability of our approach of treating the reference polarization in constant-D simulations. Note that the values for D_x are always larger compared to P_x, due to the dielectric effect. After this consistency check, the D derivative estimates of the relative permittivity κ were computed by performing constant-D_x simulations for a field strength ranging from 0.5 × 10⁴ to 20 × 10⁴e Å^–2.

Table 2. Simulation Conditions at Constant-E_x or Constant-D_x and the Corresponding Observed ⟨P_x⟩ for System C at T = 150 K^a.

Ex (V Å–1)	⟨Px⟩ (104 e Å–2)	Dx (104 e Å–2)	⟨Px⟩ (104 e Å–2)
0.01	3(1)	3.15	2.6(6)
0.02	3.5(4)	4.60	3.6(4)
0.03	3.8(2)	5.47	3.9(1)
0.04	4.0(1)	6.22	4.04(9)
0.05	4.2(1)	6.92	4.18(8)
0.10	4.62(6)	10.15	4.63(5)
0.19	5.21(3)	15.71	5.21(3)
0.28	5.70(3)	21.18	5.70(2)
0.50	6.78(1)	34.41	6.78(1)

^aTo give an impression for the sampling error, ±2σ is given as statistical error.

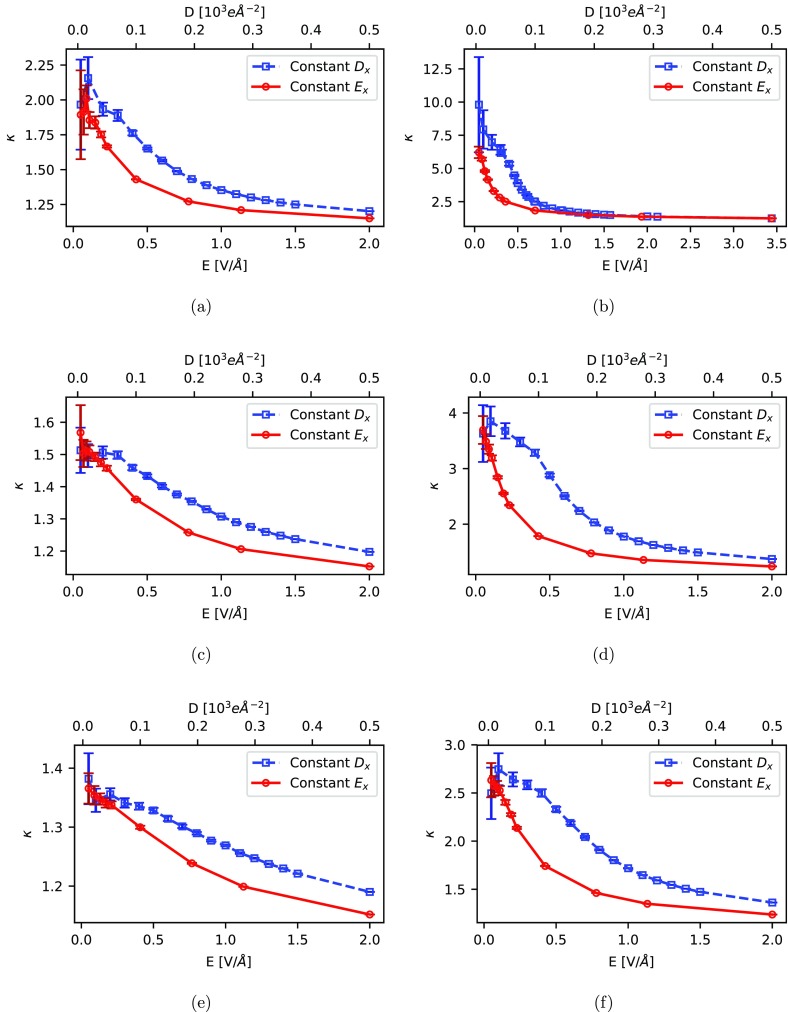
Figure 4 shows the comparison of κ, obtained as a function of E and D for systems B and C at all investigated temperatures. The relative permittivity has to be obtained by an extrapolation to zero field. All in all, this yields results comparable to those from polarization fluctuations listed in Table 1. As already observed by Zhang and Sprik in the case of liquid water, this extrapolation is somewhat more difficult for the constant-E method due to the steeper slope of the curve at the intercept. However, as it can be seen from the error bars, the sampling error is increasing substantially for decreasing field strengths. This is especially pronounced in the case of the constant-D simulations due to the disadvantageous dependence of the statistical error on the polarization ⟨P⟩ (see eq S6), which makes the extrapolation equally error prone. Furthermore, for the constant-D approach it has to be taken into account that, in the case of periodic polymers like an MOF, the reference polarization has to be determined beforehand, which renders this method numerically less efficient. Overall, from our analysis we recommend computing κ from polarization fluctuations at E = 0 as long as the saturation for finite field is not of relevance.

Figure 4.

Static relative permittivity κ_x obtained from fixed-E_x and fixed-D_x simulations for system B at (a) 150 K, (c) 298 K, and (e) 450 K and system C at (b) 150 K, (d) 298 K, and (f) 450 K. To give an impression for the sampling error, ±2σ is plotted as statistical error.

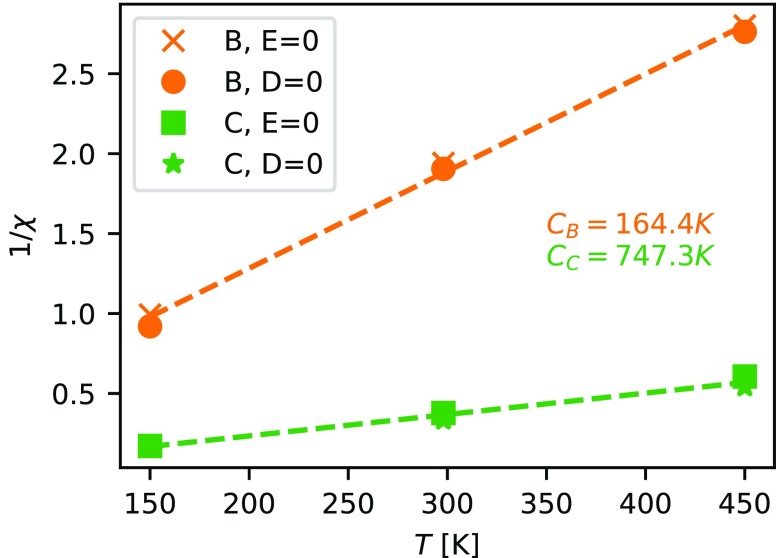
Further information on the coupling of the dipolar groups can be gained by analyzing the temperature dependence of systems B and C by a Curie–Weiss plot (Figure 5). Here, the inverse of the electric susceptibility χ = κ – 1 is plotted as a function of temperature. According to the Curie–Weiss law for paraelectric materials (or ferroelectrics beyond the Curie temperature) a linear relationship is expected with

8

where the Curie constant C is equal to the inverse of the slope. As expected, with C = 747 K a substantially larger Curie constant is observed for system C as compared to B with C = 164 K, since C should be proportional to the square of the dipole moment μ. Indeed, the ratio of the Curie constants () is roughly equal to the ratio of the squared dipole moments (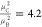). The so-called Weiss constant θ provides information about the ground state of the material at 0 K. A value of θ > 0 indicates a ferroelectric ground state, and for θ < 0 it should be antiferroelectric, whereas for θ = 0 it is paraelectric (no coupling of the dipoles). Our results predict Weiss constants close to zero, indicating only weak interactions between the individual dipoles, which can be rationalized by the porosity of the MOFs and the consequently large spacial separation of the dipoles. For system B, a negative Weiss constant of θ_B = −10.9 K is found, whereas a positive value is predicted for system C (θ_C = 24.7 K). However, for both systems an antiferroelectric ground state is to be expected, since this is clearly indicated by model calculations for simple orthorhombic dipole lattices.³⁹ The slightly positive Weiss constant for system C can be explained by the in general weak interactions of the dipoles and the dependency on statistical errors of the predicted dielectric constants.

Figure 5.

Inverse of the electric susceptibility χ for systems B and C, obtained by the two fluctuation methods as a function of temperature T. The dashed lines show a linear regression curve to the data sets obtained for both systems.

Field Induced Breathing Behavior

As already discussed, Ghoufi and co-workers observed an electric field induced breathing of MIL-53(Cr) in a theoretical simulation at high field strength.¹² One of us proposed a mechanism for this behavior, by invoking a model of a 2D grid of induced dipoles.¹³ As shown in the upper panel of Figure 6, the application of an electric field results in a lattice of induced dipoles, oriented along an axis of the unit cell, located mainly at the inorganic building blocks due to the relatively large and alternating charges. The electrostatic interaction between the dipoles depends on the shape of the lattice. By a wine-rack deformation to a rhombic shape the attractive interactions can be increased. Note that the term ΩEP in the electric enthalpy 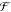does not depend on the volume of the system (eq 2). Thus, the interactions between the induced dipoles are responsible for the transformation, whereas the electric field is just the source for the necessary polarization.

The here investigated systems with dipolar rotors should in principle give rise to the same wine-rack-type breathing deformation as observed in MIL-53(Cr). However, the critical field strength E_c, which is necessary to trigger the structural transformation, should depend on the strength of the incorporated dipolar organic moieties. Furthermore, since the field strength required to orient the permanent dipoles (lower panel of Figure 6) is lower than that to induce equally strong dipoles, a lower E_c should be expected in the case of a system with rotatable dipolar groups.

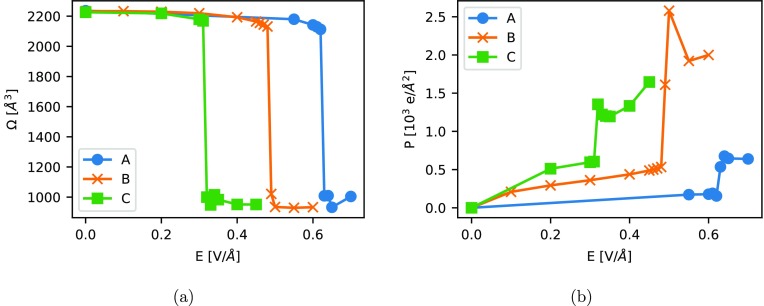
To prove this, we performed molecular dynamics simulations in the NσT ensemble, allowing for cell deformations at increasing field strength E_x for systems A–C at 298 K. Figure 7a shows the unit cell volume Ω as a function of the electric field. As expected, in all three cases the structure collapses to a closed pore form at sufficiently high field. It should be noted that the force-field was parametrized with respect to the sterically relaxed building blocks (see Figure S1). Thus, the force-field becomes less accurate for high deformation (see Figure S2) and potentially underestimates the unit cell volumes of the contracted form. However, the critical field strength E_c, at which the contraction sets in, is unaffected by this. The simulations show that dipolar groups favor the transition: whereas system A transforms at ≈0.6 V Å^–1, system B already contracts at ≈0.5 V Å^–1 and C even at only ≈0.3 V Å^–1. In Figure 7b, the polarization P_x is plotted as a function of the electric field E_x. For all three systems a jump in P_x is observed at the critical field strength due to the volume contraction. Interestingly, systems B and C show almost the same value for the critical polarization needed to trigger the contraction (≈5 × 10⁴e Å^–2). A comparison with Figure 2 indicates that these values lie above the region of orientation polarization for both materials, which means that additional buildup of displacive polarization is needed to reach the critical level for the collapse. However, when the amount of ionic polarization is smaller, the dipole of the oriented linkers becomes larger, leading to a lower E_c for system C. Consequently, to reach contraction purely by means of orientation polarization, organic moieties carrying even larger dipole moments would have to be incorporated into the framework. Then, the field-driven breathing would be temperature-dependent, since the required field strength needed to reach the critical polarization would also be temperature-dependent. As expected, system A needs a higher electric field E_c for the contraction, but to our surprise a smaller critical polarization (≈0.2 × 10⁴e Å^–2) is necessary. Note that in system A the polarization is mainly induced directly at the inorganic zinc paddle-wheels, which actually serve as hinges during the contraction, potentially lowering the critical polarization.

Figure 7.

Simulation of systems A–C at 298 K in the NσT ensemble at different electric field strengths E_x: (a) unit cell volume as a function of the applied electric field E_x; (b) polarization P_x as a function of the applied electric field E_x.

Conclusions and Outlook

In this work, we demonstrated that dipolar rotors used as linkers in MOFs have a strong impact on the electric permittivity κ of the materials and can be used to tune their electric response. The herein investigated systems exhibit substantially larger dielectric constants as expected for MOFs in general and exhibit a strong dependency on the chemical composition of the dipolar linker moiety, i.e., on its dipole moment. In addition, a strong temperature dependence of κ was observed, which obeys the Curie–Weiss law for paraelectric materials. The investigated materials exhibit an anisotropic dielectric response. They are paraelectric in the x- and y-direction and dielectric in the z-direction. This offers new opportunities for the design of specialized dielectric sensors. Future efforts will aim to investigate the effect of adsorbed guest molecules on the dielectric permittivity.

In addition we found that the easiest and most efficient method to calculate κ from molecular dynamics simulations is to compute them from polarization fluctuations at zero field, since this makes the need for a reference polarization obsolete. Reference polarizations are needed to tackle the multivaluedness of the polarization as soon as the computation of the dielectric constant depends somehow on the absolute value of the polarization.

Furthermore, the field induced wine-rack-type lattice contraction of the investigated systems was studied with respect to the influence of the dipolar linkers. As observed before by Ghoufi et al. for MIL-53(Cr), a similar breathing behavior was found to be present for the pillared-layer MOFs. However, the dipolar linkers are able to reduce the critical field strength needed to trigger the contraction, depending on the magnitude of the incorporated dipole moment. With even higher dipole moments and in combination with guest adsorption, even lower critical field values E_c could be possible, allowing for new routes of potential application of MOFs with rotatable dipolar linkers in sensing or gas separation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00497.

• Detailed information about the MOF-FF energy expression and the parameter sets used within the MD simulations (PDF)

The authors declare no competing financial interest.