Mathematical modeling of the heterogeneous distributions of nanomedicines in solid tumors

Abstract

The distribution of nanomedicines inside solid tumors is often restricted to perivascular areas, leaving most distal tumor cells out of reach. This partly explains modest patient benefit of many nanomedicines compared to their free-form counterparts. The objective for this study is to develop a mathematical model to quantitatively analyze this phenomenon and the influencing factors to such perivascular distribution and seek for effective strategies to alleviate this. A spatial tumor distribution model was firstly constructed to mimic the geometrical structure of tumor vessels and the surrounding tumor cells. This tumor model was further integrated with a systemic pharmacokinetics model for nanoparticles. A variety of factors on the tumor spatial distributions of nanomedicines were considered in the model. With the model, we quantified the effect of these influencing factors on tumor delivery efficacy (ID %), the magnitude of heterogeneous distribution (H index), and the effect of enhanced permeability and retention (EPR). In particularly, we compared the spatial distributions of the nanoparticles and the free payloads insides tumors. The model predicted high degrees of distributional heterogeneity for both nanoparticles and free payloads. The degree of heterogeneity and the influencing factors for free payloads were markedly different from those for nanoparticles. We found that nanoparticle diffusion coefficient was the most effective factor in reducing the nanoparticle H index but exerted moderate influence on the free payloads H index. The most effective factor in reducing the H index of free payload was payload diffusion coefficient. The factors that improved free payload distribution were closely associated with higher drug efficacy. In contrast, the factors that improved nanoparticle spatial distributions did not always confer improved anti-tumor efficacy of the delivered drug. These findings highlight the importance of assessing the heterogeneous free payload distribution in tumors for the development of effective nanomedicines.

Introduction

Nanomaterials have been used as drug carriers to enhance the selective delivery of anticancer agents to solid tumors [1–3]. Despite the initial success in preclinical studies, the therapeutic benefit of many cancer nanomedicines in patients is quite modest. Many FDA-approved nanomedicines offer only limited improvements in patient survival compared to their conventional therapies [2]. Many licensed nanomedicines, such as Doxil®, Myocet®, PICN®, and DaunoXome®, have based their registrations on the reduced adverse effects rather than any improved therapeutic benefits [2]. Doxil, for instance, was approved due to its substantially lower cardiovascular toxicity compared to the free agent doxorubicin. No significant improvement in patient survival has been documented yet for Doxil [3].

The enhanced permeability and retention (EPR) effect provides the key rationale for using nanomedicines in the treatment of solid tumors [4]. The EPR theory was originally applied to explain the enhanced accumulation of nanoparticles within tumors with leaky vasculature and poor lymphatic drainage [5]. Unfortunately, the EPR effect has not broadly translated into clinic yet. Most nanomedicines have failed to provide superior efficacy compared to their free drug counterparts in clinical trials [2]. In patients, the tumor microenvironment is often complicated by a high density of tumor cells, irregular vascular distribution, poor blood flow, and substantially elevated interstitial fluid pressure [1]. These factors hamper the selective and homogenous delivery of nanodrugs into tumors, resulting in highly heterogeneous and perivascular distribution [6–10]. This perivascular distribution and the resultant local release of free payloads means that only tumor cells in the vicinity of blood vessels are accessible to nanomedicines, leaving distal tumors out of reach and restricting the therapeutic potential of nanomedicines for cancer treatment. Spatial distributional heterogeneity is largely responsible for the modest survival benefits offered by many FDA-approved nanomedicines [11].

In order to improve the spatial distribution of nanoparticles in solid tumors, many strategies have been investigated (Table 1), including (1) improving nanoparticle stability to increase systemic half-life and prolong tumor delivery duration [12–14]; (2) augmenting the tumor blood supply [15–18]; (3) increasing the tumor vessel permeability [10, 14, 19–21]; (4) modifying the nanoparticle physiochemical properties to achieve local release into the tumor microenvironment [10, 22, 23]; and (5) improving nanoparticle diffusion through the compressed tumor extracellular matrix [24]. These strategies (influencing factors) have been broadly evaluated in xenograft models, and some have demonstrated improved tumor delivery efficiency and enhanced anti-tumor efficacy. However, most of these strategies have not yet advanced beyond the academic laboratory [21]. Additional research and development are needed before these strategies can be translated into clinical practice. Thus, it will be useful to quantitatively compare these strategies as further nanomedicine improvements are sought.

Table 1.

A summary of assessed factors and associated therapeutic strategies.

Influencing factors	Evaluated range		Relevant properties and therapeutic strategies
CL: nanoparticle systemic clearance	100 mL/h for Doxil in a 70 kg man [26]. Dynamic range: 5 ~ 500 mL/h.		Particle size: ideal range 80 ~ 200 nm. A smaller size is filtered out by kidney (< 5 nm) or interacts with hepatocytes (< 50 nm); a larger size (> 200 nm) is quickly eliminated by mononuclear phagocyte system (MPS) [12, 13]. Optimal charge range: weakly negative to near neutral [14]. Polymer: PEGylated or other polymers [12].
BP: tumor blood perfusion	60 mL/h for a 10 g tumor spheroid in a 70 kg man. Dynamic range: 6 ~ 600 mL/h [28].		Vasoconstrictors: Vasoconstrictors (e.g., Angiotensin II): increase BP and trans-capillary pressure [16]. Vasodilators: Vasodilators (e.g. captopril, nitroglycerin): restore tumor BP by decreasing flow resistance [17, 18]. Hyperthermia: Mild elevation of body temperature could increase BP [19].
VP: nanoparticle vascular permeability	0.175% (~ 0.105 mL/h) of tumor blood perfusion for a 10 mL tumor spheroid in a 70 kg man [31, 32]. Dynamic range: 0.003% ~ 3% of tumor blood perfusion.		Vasculature normalization: decreases interstitial fluid pressure and thereby restores trans-capillary pressure for high VP, such as anti-VEGFR antibodies (e.g., ramucirumab, DC101) and VEGFR tyrosine kinase inhibitors (e.g. Cediranib and pazopanib) [21, 23]. Vascular membrane: increases vascular permeability by promoters to reduce the barrier functions. (e.g., tumor necrosis factor, histamine, nicotinamide, NO donors) [14, 24, 29]. Optimal size: small size nanoparticles [10].
DC: Nanoparticle diffusion coefficient in compressed extracellular matrix (ECM)		5·10−11 cm2/s for 100 nm nanoparticles in tumors and > 5-fold lower in deeper tumor matrix [34]. Dynamic range: 4.5·10−9 ~ 4.5·10−12 cm2/s.	Normalization of tumor matrix by e.g., losartan, relaxin collagenase, and hyaluronidase, modulates the compressed ECM and reduces the interstitial fluid pressure [26, 27]. Optimal size: small size nanoparticles [10].
RC: Nanoparticle release constant in tumor interstitial space		0.0127 /h−1 for Doxil in a 70 kg man. Dynamic range: 0.001 ~ 1 h−1.	Stimuli-responsive: light-responsive, ultrasound-responsive, and thermo-responsive [28].

This study used Doxil as a model drug to develop a physiologically-based tumor distribution model to 1) describe the heterogeneous distributions of nanoparticles and their free payloads in solid tumors, and 2) jointly assess these potentially influencing factors to make systematic comparisons. Cytotoxic drugs in encapsulated form are generally not directly bioavailable to tumor cells; free payloads are the cytotoxic component of most anti-cancer nanomedicines. Our analysis particularly focused on the spatial distribution of free payloads in solid tumors. The effects of these influencing factors were quantitatively evaluated and compared using the developed mathematical platform. The most influential factors and their potential combined effects were also evaluated. The reasons that nanomedicines have failed to translate into improved patient survival rates were also explored.

Methods

The mathematical framework

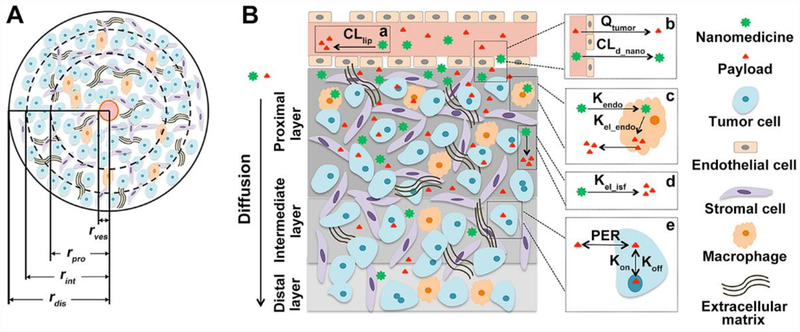
The mathematical framework that was developed in this study largely adopted the assumptions of the Krogh cylinder model to describe the geometrical structure of tumor blood vessels and the spatial distribution of nanoparticles and their free payloads in the vessel surrounding tumor tissues (Figure 1) [25]. This model assumes that the capillary is embedded on the axis of a cylindrical tumor region with tumor cells surrounding the vessels and that a bulky tumor is composed of many such cylindrical tumor regions. In the developed model, the cylinder radius was set to 100 μm, and the vessel radius was set to 7.5 μm [25]. The effects of high interstitial fluid pressure and the compressed extracellular matrix, factors that are responsible for distributional heterogeneity, were considered in this model using reduced nanoparticle diffusion rates and limited diffusible space within the tumor extracellular space. Each cylinder was assumed to be composed of three anatomical layers of tumor cells (proximal, intermediate, and distal), distinguished by their distance from the embedded capillary. Three radius ratios between tumor layers (proximal: intermediate: distal) were evaluated in this study to better mimic the heterogeneous tumor microenvironment: (1) 60: 30: 10 for well-diffused tumor microenvironment, (2) 30: 40: 30 for moderately-diffused tumor, and (3) 10: 30: 60 for poorly-diffused tumor.

Figure 1.

Schematic structure of the developed model. (A) A cylinder tumor spheroid. Each tumor spheroid is divided into three anatomical layers (proximal, intermediate, and distal), distinguished by their distance from the embedded central capillary. The red circle represents the central blood vessel. (B) Nanomedicine disposition kinetics in tumors. The longitudinal section depicts three tumor layers and diagrams on the right depicts nanomedicine disposition kinetics in tumors. a) releases of payloads in plasma from nanoparticles; b) nanoparticle and payloads extravasation; c) local sequestration of nanoparticles by tumor macrophages and then release of payloads; d) direct release of payloads from tumor localized nanoparticles; e) taken up of paylodas by tumor cells and reversible binding kinetics to DNA to exert efficacy. CL_pnano: systemic clearance of nanomedicine; Q_tumor: blood flow in tumor; K_endo: uptake rate constant of nanomedicine by tumor cells; K_elendo: intracellular nanomedicine release rate constant; K_elisf: interstitial nanomedicine release rate constant; PER: cell membrane permeability; K_on: doxorubicin-DNA association constant; K_off: doxorubicin-DNA dissociation constant.

The systemic pharmacokinetic parameters of the encapsulated and free doxorubicin in a 70-kg man are shown in Table 2 [26, 27]. The parameters for the three anatomical tumor layers were summarized in Table 3 [28–30], and the particle/payload dispositional parameters were documented in Table 4 [31–35]. All model parameters were obtained either from the literature or optimized using experimental data.

Table 2.

Systemic pharmacokinetic parameters of encapsulated and free doxorubicin

	Value (CV)	Unit	Source
CLd_dox	61.8	L/h	[27]
CLp_dox	112	L/h	[27]
CLp_nano	100.5	mL/h	[26]
Vc_dox	23.3	L	[27]
Vp_dox	1130	L	[27]
Vnano	5086	mL	[26]

Table 3.

Tumor physiological parameters [28, 30]

			Value			Unit
	Parameter Definition	Well diffused		Moderately diffused	Poorly diffused
Q	Tumor blood perfusion	60				mL/h
CDNA	DNA concentrations	0.382				μmol/mL
S1	Surface area of tumor cells in the proximal layer	17677		5303	982	cm2
S2	Surface area of tumor cells in the intermediate layer	19445		18070	7660	cm2
S3	Surface area of tumor cells in the distal layer	8053		21802	36532	cm2
VL1e	Intracellular volume of the tumor cells in the proximal layer	3.115		0.935	0.173	mL
VL1em	Intracellular volume of macrophage cells in the proximal layer	0.0078		0.0023	0.0004	mL
VL1i	Interstitial volume of the proximal layer	0.779		0.233	0.0433	mL
VL2e	Intracellular volume of the tumor cells in the intermediate layer	3.427		3.184	1.350	mL
VL2em	Intracellular volume of macrophage cells in the intermediate layer	0.0086		0.0080	0.0034	mL
VL2i	Interstitial volume of the intermediate layer	0.857		0.796	0.337	mL
VL3e	Intracellular volume of the tumor cells in the distal layer	1.419		3.842	6.44	mL
VL3em	Intracellular volume of macrophage cells in the distal layer	0.0036		0.0096	0.0161	mL
VL3i	Interstitial volume of the distal layer	0.355		0.961	1.61	mL

Table 4.

Values of model parameters employed in the analysis

	Value (CV)			Unit	Source
	Well diffused	Moderately diffused	Poorly diffused
PER	0.0756			cm/h	Optimized
CLd_nano	0.10512			mL/h	[31, 32]
h	0.5358			-	Optimized
k	0.419			1/h	Assumption
K12_dox	39.1	7.16	2.42	1/h	[33]
K21_dox	3.24	1.73	2.31	1/h
K12_nano	1.95E-2	3.57E-3	1.21E-3	1/h	[34]
K21_nano	8.08E-4	4.31E-4	5.77E-4	1/h
K23_dox	3.96	0.143	9.58E-3	1/h	[33]
K32_dox	0.436	4.88E-2	7.47E-3	1/h
K23_nano	4.28E-4	8.69E-6	3.30E-7	1/h	[34]
K32_nano	4.71E-4	3.00E-7	3.00E-8	1/h
Kel_endo	0.0576			1/h	[29]
Kel_isf	0.0127			1/h	Optimized
Kendo	0.00105			1/h	[35]
Koff	1.2E03			1/min	[29]
Kon	1.2E06			1/(min·μmol/mL)	[29]
Kp_dox	3.6			-	Optimized
Kpp	2.28			-	Calculated
Kpt_dox	1			-	Assumption

Systemic pharmacokinetics

The compartmental model was applied to describe the systemic disposition of Doxil and free doxorubicin. All symbols and parameter definitions are provided in the Supplement material (Table S1). Nanoparticle plasma concentration was described as Equation (1):

$$d{C}_{pnano}/dt=-\left(C{L}_{pnano}\times C_{pnano}+C{L}_{dnano}\times C_{pnano}\right)/V_{nano}$$ (1)

Where C_pnano is plasma nanomedicine concentration, CL_pnano denotes systemic clearance (e.g., elimination by liver and macrophages) while CL_dnano depicts tumor distribution of nanomedicine, V_nano is apparent distribution volume of nanoparticles.

The pharmacokinetic profile of free payload (doxorubicin) was described by a two-compartment model using Equations (2) and (3).

Free payload kinetics in plasma compartment:

$$d{C}_{cdox}/dt=[C{L}_{pnano}\times C_{pnano}–C{L}_{pdox}\times C_{cdox}–(C_{cdox}–C_{L1isfdox}/K_{ptdox})\times Q–C{L}_{ddox}\times (C_{cdox}-C_{pdox})]/V_{cdox}$$ (2)

Free payload kinetics in tissue compartment:

$$d{C}_{pdox}/dt=C{L}_{ddox}\times \left(C_{cdox}–C_{pdox}\right)/V_{pdox}$$ (3)

Where C_cdox and C_pdox denote doxorubicin concentrations in plasma and tissue compartments, V_cdox and V_pdox denote volumes of distribution at plasma and tissue compartment. CL_pdox and CL_ddox are systemic clearance and tissue distribution clearance of payload, Q is blood flow in tumor and K_ptdox is interstitial fluid/plasma partition coefficient. C_L1isfdox represent interstitial concentration in the proximal layer, where L1 represents the proximal layer, Likewise, L2 and L3 in the following Equations represent the intermediate and distal layers.

Intratumor spatial distribution

After extravasation, the encapsulated doxorubicin molecules (or intact nanoparticles) that accumulate in the proximal layer can be characterized into one of three dispositional fates: their payload is released, they diffuse into the intermediate tumor layer, or they are taken up by local macrophages. The kinetics of intact nanoparticles in the proximal tumor layer are described by Equation (4).

$$d{C}_{L1isfnano}/dt=C{L}_{dnano}\times C_{pnano}/V_{L1i}–K_{12nano}\times C_{L1isfnano}+K_{21nano}\times C_{L2isfnano}–C_{L1isfnano}\times \left(K_{endo}+K_{elisf}\right)$$ (4)

Where C_L1isfnano and C_L2isfnano are nanomedicine concentrations in the proximal and intermediate layers, V_L1i is interstitial volume of the proximal layer, K_12nano is nanomedicine diffusion rate constant across the proximal and intermediate layer, K_21nano is nanomedicine diffusion rate constant from the intermediate back to proximal layer, K_endo is uptake rate constant of nanomedicine by tumor cells and K_elisf is nanomedicine release rate constant.

In tumors, about 0.25% of the cells are macrophages [30]. The encapsulated doxorubicin could be transiently sequestrated by local macrophages, leading to a subsequent release of free doxorubicin, as depicted in Equation 5.

$$d{C}_{L1endonano}/dt=K_{endo}\times C_{L1isfnano}\times V_{L1i}/V_{L1em}–K_{elendo}\times C_{L1endonano}$$ (5)

Where C_L1endonano represents intracellular nanomedicine concentration and V_L1em is intracellular volume of the macrophage cells in the proximal layer, K_elendo describes nanomedicine intracellular release rate constant.

In this model, only the released doxorubicin exerts an anti-tumor effect. The concentrations of free doxorubicin in the proximal layer derive from either the release of local nanoparticles or direct diffusion from blood vessels. The concentrations of free doxorubicin in the proximal tumor layer is provided in Equation 6, below.

$$d{C}_{L1isfdox}/dt=(C_{cdox}–C_{L1isfdox}/K_{ptdox})\times Q/V_{L1i}–PER\times S_{L1}/V_{L1i}\times [C_{L1isfdox}–C_{L1endodox}/(K_{pdox}\times K_{pp})]+K_{elisf}\times C_{L1isfnano}+K_{elendo}\times C_{L1endonano}\times V_{L1em}/V_{L1i}–K_{12dox}\times C_{L1isfdox}+K_{21dox}\times C_{L2isfdox}$$ (6)

Where S_L1 denotes total cell surface area and C_L1endodox denotes free doxorubicin concentration in the tumor cells of the proximal layer. PER is cell membrane permeability, K_pdox is partition coefficient of doxorubicin in tumor cells, K_pp denotes pH determined partition coefficient between intracellular and extracellular spaces, K_12dox is doxorubicin diffusion rate constant across the proximal and intermediate layer, K_21dox is doxorubicin diffusion rate constant from the intermediate back to proximal layer, C_L2isfdox is doxorubicin concentration in the intermediate tumor layer.

Tumor intracellular kinetics

Once the free doxorubicin is taken in by tumor cells, it reversibly binds to DNA nucleotides [36]. The concentrations of DNA-bound doxorubicin in the proximal layer is shown in Equation (7).

$$d{C}_{L1DNA}/dt=K_{on}\times C_{L1endodox}\times C_{DNA}–K_{off}\times C_{L1DNA}$$ (7)

Where C_L1DNA represents DNA bound doxorubicin concentrations in the proximal tumor layer, K_on and K_off denote doxorubicin-DNA association and dissociation constants, C_DNA is the concentration of DNA binding sites.

The concentrations of doxorubicin in the proximal layer is described by Equation (8).

$$d{C}_{L1endodox}/dt=PER\times S_{L1}/V_{L1e}\times [C_{L1isfdox}–C_{L1endodox}/(K_{pdox}\times K_{pp})]–K_{on}\times C_{L1endodox}\times C_{DNA}+K_{off}\times C_{L1DNA}$$ (8)

Where V_L1e is intracellular volume of the tumor cell in the proximal layer and other parameters have described above.

The disposition processes of both encapsulated and free doxorubicin in the intermediate and distal tumor layers are detailed below. For the intermediate layer, calculations are provided for the disposition of the interstitial nanoparticles, the intracellular nanoparticles, the free doxorubicin, the DNA-bound doxorubicin, and the intracellular free doxorubicin. Equation (9) describes the nanoparticles disposition at the intermediate tumor layer:

$$d{C}_{L2isfnano}/dt=K_{12nano}\times C_{L1isfnano}–K_{21nano}\times C_{L2isfnano}–K_{23nano}\times C_{L2isfnano}+ K_{32nano}\times C_{L3isfnano}–C_{L2isfnano}\times \left(K_{endo}+K_{elisf}\right)$$ (9)

Where C_L3isfnano represents interstitial nanomedicine concentrations in the distal layer, K_23nano is nanomedicine diffusion rate constant between the intermediate and distal layer, K_32nano is nanomedicine diffusion rate constant from the distal back to intermediate layer. Equation (10) describes intracellular nanoparticles disposition at the intermediate tumor layer:

$$d{C}_{L2endonano}/dt=K_{endo}\times C_{L2isfnano}\times V_{L2i}/V_{L2em}–K_{elendo}\times C_{L2endonano}$$ (10)

Where C_L2endonano is intracellular nanomedicine concentration in the intermediate layer, V_L2i is interstitial volume of the intermediate layer and V_L2em is intracellular volume of the macrophage cells in the intermediate layer.

Equation (11) describes free doxorubicin disposition at the intermediate tumor layer:

$$d{C}_{L2isfdox}/dt=K_{12dox}\times C_{L1isfdox}–K_{21dox}\times C_{L2isfdox}+K_{elisf}\times C_{L2isfnano}+K_{elendo}\times C_{L2endonano}\times V_{L2em}/V_{L2i}–\{PER\times S_{L2}/V_{L2i}\times [C_{L2isfdox}–C_{L2endodox}/(K_{pdox}\times K_{pp})]\}–K_{23dox}\times C_{L2isfdox}+K_{32dox}\times C_{L3isfdox}$$ (11)

Where S_L2 denotes total cell surface area of the intermediate layer, C_L2endodox is intracellular free doxorubicin concentration in the intermediate layer, K_23dox describes free doxorubicin diffusion rate constant between the intermediate and distal layer, K_32dox is doxorubicin diffusion rate constant from the distal back to intermediate layer. C_L3isfdox is interstitial free doxorubicin concentration in the distal layer.

Equation (12) describes the concentration of the DNA-bound doxorubicin at the intermediate tumor layer:

$$d{C}_{L2DNA}/dt=K_{on}\times C_{L2endodox}\times C_{DNA}–K_{off}\times C_{L2DNA}$$ (12)

Where C_L2DNA and C_L2endodox are DNA bound and intracellular free doxorubicin concentrations in the intermediate layer of tumor.

Fin0061lly, Equation (13) describes the intermediate layer disposition of the intracellular free doxorubicin:

$$d{C}_{L2endodox}/dt=PER\times S_{L2}/V_{L2e}\times [C_{L2isfdox}–C_{L2endodox}/(K_{pdox}\times K_{pp})]–K_{on}\times C_{L2endodox}\times C_{DNA}+K_{off}\times C_{L2DNA}$$ (13)

Where V_L2e is intracellular volume of the intermediate tumor layer.

For the distal layer, calculations are provided for the disposition of the interstitial nanoparticles, the intracellular nanoparticles, the free doxorubicin, the DNA-bound doxorubicin, and the intracellular free doxorubicin. Equation (14) describes nanoparticle disposition at the distal tumor layer:

$$d{C}_{L3isfnano}/dt=K_{23nano}\times C_{L2isfnano}–K_{32nano}\times C_{L3isfnano}–C_{L3isfnano}\times \left(K_{endo}+K_{elisf}\right)$$ (14)

Equation (15) describes intracellular nanoparticles at the distal tumor layer:

$$d{C}_{L3endonano}/dt=K_{endo}\times C_{L3isfnano}\times V_{L3i}/V_{L3em}–K_{elendo}\times C_{L3endonano}$$ (15)

Where C_L3endonano is intracellular nanomedicine concentration in the distal layer, V_L3i is interstitial volume of the distal layer and V_L3em is intracellular volume of the macrophage cells in the distal layer.

Equation (16) describes free doxorubicin disposition at the distal tumor layer:

$$d{C}_{L3isfdox}/dt=K_{23dox}\times C_{L2isfdox}–K_{32dox}\times C_{L3isfdox})+K_{elisf}\times C_{L3isfnano}+K_{elendo}\times C_{L3endonano}\times V_{L3em}/V_{L3i}–\left\{PER\times S_{L3}/V_{L3i}\times [C_{L3isfdox}–C_{L3endodox}/(K_{pdox}\times K_{pp})]\right\}$$ (16)

Where S_L3 is total cell surface area and C_L3endodox is intracellular free doxorubicin concentration in tumor cell of the distal layer, K_23dox is free doxorubicin diffusion rate constant between the intermediate and distal layer.

Equation 17 describes the concentration of DNA-bound doxorubicin at the distal tumor layer:

$$d{C}_{L3DNA}/dt=K_{on}\times C_{L3endodox}\times C_{DNA}–K_{off}\times C_{L3DNA}$$ (17)

Where C_L3DNA and C_L3endodox represent DNA bound and intracellular free doxorubicin concentrations in the intermediate layer of tumor.

Finally, Equation (18) describes the intracellular free doxorubicin at the distal tumor layer:

$$d{C}_{L3endodox}/dt=PER\times S_{L3}/V_{L3e}\times [C_{L3isfdox}–C_{L3endodox}/(K_{pdox}\times K_{pp})]–K_{on}\times C_{L3endodox}\times C_{DNA}+K_{off}\times C_{L3DNA}$$ (18)

Where V_L3e is intracellular volume of the intermediate layer.

Tumor delivery efficiency

The developed model was first applied to simulate the concentration-time profiles of nanoparticles and free doxorubicin in the three anatomical tumor layers. The distal tumor layer was expected to accumulate a much lower level of drugs than the proximal layer. Given the simulated time window (60 hours), tumor death was not considered in the model. The degree of distributional heterogeneity was evaluated by comparing the concentration gradients of the nanoparticles and the free doxorubicin among the three anatomical layers.

Delivery efficiency, or the percentage of injected dose (ID%), was calculated as set forth in Equation (19) by adding the accumulated drug concentrations (in either free or encapsulated forms) in the three tumor anatomical layers [37]:

$$Deliveryefficiency\left(ID\%\right)=\left(AU{C}_{L1t}+AU{C}_{L2t}+AU{C}_{L3t}\right)/Duration\times V_{tumor}/Dose$$ (19)

where AUC_L1t, AUC_L2t and AUC_L3t represents the drug exposure (area under the concentration vs time curves) in the proximal, intermediate and distal anatomical tumor layers, Duration is the simulated time window, Dose is the amount of drug administered, and V_tumor is tumor volume.

Three quantitative metrics

Three quantitative metrics were developed to evaluate the degree of distributional heterogeneity and its subsequent impact on the drug’s overall anti-tumor effect.

Concentration gradients across the three anatomical tumor layers

The degree of distributional heterogeneity is characterized by the concentration gradients of either free or encapsulated drugs across the three anatomical tumor layers. The heterogeneity index (H index) is defined as:

$$Hindex=1/3\times (AU{C}_{L2}/AU{C}_{L1}+AU{C}_{L3}/AU{C}_{L1}+AU{C}_{L3}/AU{C}_{L2})$$ (20)

Where AUC_L1, AUC_L2 and AUC_L3 represent the exposures of either free or encapsulated doxorubicin in the three anatomical tumor layers after a single dose of Doxil (50 mg/m²). The H indexes for free payloads and nanoparticles are separately defined. A lower H index value indicates a higher degree of heterogeneity. When the H index = 1, uniform distribution is indicated across the three anatomical tumor layers. When H = 0, all the drugs are predicted to accumulate in the perivascular regions, and none of the nanoparticles migrate away from the vessels to the distal tumor layers.

The EPR effect

In general, free doxorubicin in tumors derives from two sources: release from local nanoparticles within tumors and direct diffusion from the blood circulation. To quantitatively understand the fraction of free payloads within tumors that derives from the release of local nanoparticles, we simulated a hypothetical situation with no nanoparticle tumor delivery (i.e., zero EPR effect), where all the free doxorubicin in the tumors was supplied by the direct diffusion of free doxorubicin from the blood circulation, denoted as Drug_-EPR. The calculation of the differences in the free doxorubicin exposure between instances with (Drug_+EPR) and without (Drug_-EPR) EPR-dependent accumulation predicted the EPR contribution (EPRC) to tumor drug delivery. The EPRC was then defined as set forth in Equation (21).

$$EPRC=\left(Dru{g}_{+EPR}–Dru{g}_{-EPR}\right)/Dru{g}_{+EPR}$$ (21)

where Drug_+EPR and Drug_-EPR represent the total amount of free payloads in the three tumor layers with or without an EPR effect. The EPRC is expected to vary between zero and one: the higher the EPRC, the larger the EPR effect. As the concentration of the free payload, the active drug form, is considered in this equation, the EPRC could also approximately indicate the EPR influence on the overall anti-tumor effect.

Anti-tumor efficacy

To translate this distributional heterogeneity into predictions of overall anti-tumor efficacy, we developed a metric to reflect the total tumor suppressive effect (TSE). A first-order tumor killing model was applied to predict the fraction of tumor cells killed at each anatomical layer after a drug exposure of duration (t). For simplicity, the killing coefficient (k) was assumed to be equal at all three tumor layers. The TSE was then defined as set forth in Equation (22).

$$TSE=1–1/3\times \left[exp\left(–k\times C_1{}^h\times t\right)+exp\left(–k\times C_2{}^h\times t\right)+exp\left(–k\times C_3{}^h\times t\right)\right]$$ (22)

where C₁ to C₃ represents the free doxorubicin concentrations in three anatomical tumor layers, k is tumor cell-killing coefficient, h is exponential coefficient, and t is the drug exposure duration. The TSE is expected to vary between zero and one: the higher the TSE value, the stronger the overall tumor killing effect. The terms h and k were derived by optimizing results from in vitro cytotoxic studies.

Evaluation of the factors that affect heterogeneous distribution

As previously discussed, the effects of many factors on tumor delivery and spatial distribution have been investigated. These factors are generally categorized into two groups: system-associated factors and drug-associated factors. Table 1 summarizes these factors and their associated therapeutic strategies. These factors include nanoparticle systemic clearance (CL), tumor blood perfusion (BP), nanoparticle vascular permeability (VP), the nanoparticle diffusion coefficient (DC) in the tumor extracellular matrix, and the nanoparticle release constant (RC) in the tumor extracellular matrix.

We systematically compared these factors with respect to the tumor delivery efficiency (as reflected by the ID%), H index, EPRC, and TSE. The origin values of those factors were obtained from the literature or they were optimized against experimental data. The CL origin value refers to the Doxil clearance rate in a 70-kg man, which is 100 mL/h. A dynamic clearance range from 5–500 mL/h was explored; this factor is largely determined by the nanoparticles’ physiochemical properties. Tumor BP is a systemic parameter that is largely determined by tumor type, tumor location, tumor size, and the degree of vascularization. The assessed BP dynamic range was 6–600 mL/h [28]. The nanoparticle VP is associated with both the nanoparticles’ physiochemical properties and the degree of tumor vascular leakage; it is a product of two elements: tumor vessel surface area [31] and the transvascular flux constant of the selected nanomedicine [32]. The nanoparticle DC relates to both the nanoparticles’ properties and the denseness of the tumor extracellular matrix. Since tumor tissues normally have high interstitial fluid pressure (IFP) and a dense extracellular matrix, especially in deeper tumor tissues, IFP and extracellular matrix coefficient were considered to influence the diffusion rates of both nanoparticle and doxorubicin. The degree of influence (defined as IFP coefficient) was associated with the anatomical layer and diffusion direction. The IFP coefficient was determined by the surface area ratio of distal to proximal layers. On the direction from proximal to distal layer, the diffusion coefficient was divided by the IFP coefficient while on the opposite direction it was multiplied by the IFP coefficient. A tumor matrix coefficient was assumed to hamper the diffusion of both nanoparticle and doxorubicin across two layers. All the diffusion coefficients will be divided by the tumor matrix coefficient. The nanoparticle RC is primarily defined by the nanoparticles’ physiochemical properties, particularly their stability in the tumor microenvironment. Many nanoparticles have been designed with selective release features that are triggered in response to tumor microenvironments or to external stimuli. In this study, the release rate origin value was optimized using Doxil experimental data from solid tumors. Table 1 summarizes the origin values and the dynamic ranges of these parameters.

Using the developed model, we quantitatively evaluated the influence of the above factors either alone or jointly on these quantitative metrics. This analysis assessed the primary contributing factors and examined whether there were any spatial distribution differences between the nanoparticles and the free payloads The potential synergistic interactions of these factors were also explored in our analysis. All the simulation and sensitivity analysis were conducted using Berkeley Madonna (version 8.3.23; http://www.berkeleymadonna.com/).

Results

Heterogeneous distribution within tumors

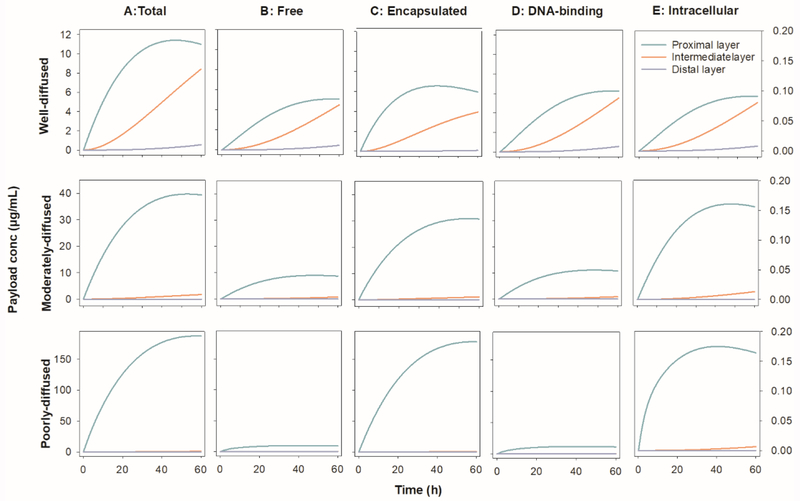
The concentration-time profiles of intact nanoparticles and free doxorubicin in three tumor anatomical layers were simulated after a single dose of Doxil in a 70-kg man (50 mg/m²). As shown in Figure 2, there was an exponential decline in the concentrations of both the nanoparticles and the free doxorubicin across the three tumor layers. Take the well-diffused rumor region as example, the concentrations of the free doxorubicin and the intact nanoparticles in the proximal tumor layer were about 11 times and 64 times higher than those in the distal tumor layer, respectively, suggesting heterogeneous distribution of both the nanoparticles and the free payloads. More than 68% of the extravasated total doxorubicin (free and encapsulated) accumulated in the perivascular region. In the proximal layer, the total doxorubicin comprised 60% encapsulated doxorubicin and 40% free doxorubicin. Diffusion condition of tumor determined the diffusion coefficient of both intact nanoparticle and free doxorubicin, which played the crucial role in their heterogeneous distribution. About 92% of the extravasated total doxorubicin accumulated in the proximal tumor layer when tumor region was moderately diffused and this ratio increased to 97% in poorly-diffused tumor.

Figure 2.

The concentration-time profiles of (A) total drug (free + encapsulated), (B) free payload, (C) encapsulated nanoparticles, (D) DNA-binding drug and (E) intracellular free drug in the three tumor anatomical layers in a 10 cm³ tumor spheroid in a 70-kg man after dosed at 50 mg/m² of Doxil.

Free doxorubicin in tumor tissues were the sum of doxorubicin in interstitial fluid, intracellular space, and DNA-binding form. Due to the high membrane permeability and rapid DNA binding, doxorubicin quickly reached equilibrium across tumor tissues. More than 98.5% of the free doxorubicin was presented as the DNA-binding form, about 1.4% was in intracellular space and less than 0.1% appeared in interstitial fluid. The diffusion condition of tumor tissues showed limited influence on the distribution of free doxorubicin. The Doxil ID% was estimated for a 10 cm³ tumor after a single 50 mg/m² dose in a 70-kg man. Table 5 summarizes the results. The tumor accumulation of the total doxorubicin ID% varied between 0.0355 and 0.0574 of the injected dose in our simulation. The diffusion condition influenced the accumulation of free doxorubicin but not the encapsulated doxorubicin. As reported in the literature (0.053 in breast cancer) [38], the accumulated nanoparticle was 0.0332% in all tested tumor regions with different diffusion conditions. The accumulated free doxorubicin varied between 0.0023% and 0.0242% from poorly-diffused to well-diffused tumor.

Table 5.

Metrics to evaluate the Doxil disposition in tumor

Tumor type	r1:r2:r3	Metrics	Proximal layer	Intermediate layer	Distal layer	Total	H index
Well diffused tumor	60:30:10	Total doxorubicin (ID%)	0.0394	0.0174	3.11E-4	0.0574	0.154
		Free doxorubicin (ID%)	0.0157	8.14E-3	2.50E-4	0.0242	0.194
		Encapsulated doxorubicin (ID%)	0.0237	9.28E-3	6.09E-5	0.0332	0.126
		EPRC	0.248	0.423	0.411	0.309
		TSE	0.0740	0.0708	0.0216	0.0555
Moderately diffused tumor	30:40:30	Total doxorubicin (ID%)	0.0402	3.32E-3	1.58E-6	0.0437	8.21E-3
		Free doxorubicin (ID%)	9.21E-3	1.20E-3	1.31E-6	0.0105	0.0130
		Encapsulated doxorubicin (ID%)	0.0310	2.12E-3	2.70E-7	0.0332	6.73E-3
		EPRC	0.303	0.554	0.511	0.332
		TSE	0.0973	0.0275	7.75E-4	0.0419
Poorly diffused tumor	10:30:60	Total doxorubicin (ID%)	0.0344	9.64E-4	2.00E-7	0.0355	1.20E-3
		Free doxorubicin (ID%)	2.06E-3	2.24E-4	2.00E-7	2.30E-3	4.65E-3
		Encapsulated doxorubicin (ID%)	0.0323	7.40E-4	0	0.0332	9.78E-4
		EPRC	0.331	0.809	1	0.378
		TSE	0.0986	0.0189	5.66E-5	0.0392

r1: radius of proximal layer, r2: radius of intermediate layer, r3: radius of distal layer.

Three quantitative metrics were also calculated based on the simulated concentration versus time profiles as shown in Figure 2. These metrics are summarized in Table 5. The H index for the nanoparticles was about 0.126, 0.00673 and 0.000978 from well- to poorly-diffused condition, which is in accordance with previous experimental observations that nanoparticles tend to accumulate in the perivascular areas with negligible amounts migrating through the compressed extracellular matrix toward the distal tumor layers. The H index for the free doxorubicin was about 0.194, 0.0130 and 0.00465 in the simulated three diffusion conditions, indicating that a high fraction of the free doxorubicin accumulated in the perivascular regions. Such high levels of perivascular accumulation for free doxorubicin have not been previously reported. The perivascular distribution of the free drug was partly associated with the perivascular distribution of the nanoparticles, but the distribution was mostly attributed to the quick diffusion of the free doxorubicin from the perivascular area back into circulation. This diffusion drastically impeded the diffusion of the free drugs across the dense tumor microenvironment toward the distal tumor layers. Unlike nanoparticles, free doxorubicin has a high vascular permeability due to its much smaller size [39]. The perivascular layer was not expected to sustain higher concentrations of free doxorubicin than the blood circulation, despite the local release of doxorubicin from the nanoparticles. Once the doxorubicin was released from the local nanoparticles into the perivascular space, a large fraction of the free doxorubicin diffused into the blood stream instead of diffusing deeper into the tumor. Only a small fraction (H = 0.295) of free drug was predicted to migrate into the distal tumor tissues, leading to a high distributional heterogeneity of free payloads within tumors.

The EPRC for Doxil was estimated to be about 30.9% (Table 5) in well-diffused tumor, indicating that about 30.9% of the free doxorubicin in the tumors was due to the EPRC (i.e., due to release from the local nanoparticles in the tumors). Even without any EPR effect (with no nanoparticle accumulation in the tumors), 69.1% of the free doxorubicin that accumulated in the tumors would have come from the blood circulation. The EPRC slightly increased to 33.8% and 37.2% in moderately and poorly diffused tumor, which might be due to the reduced tumor exposure of free doxorubicin but consistent exposure of nanoparticle. This calculation is not consistent with our previous assessments of the EPR effect, which is generally believed to substantially contribute to nanomedicine tumor accumulation, despite high clinical variability. However, in this analysis, the EPR effect may only contribute to the nanoparticle tumor accumulation but not to the free payload tumor accumulation. The EPR effect only moderately (~30%) contributed to the free payload tumor accumulation, and most of the free payload concentration diffused directly from the blood circulation.

Influence of individual factors

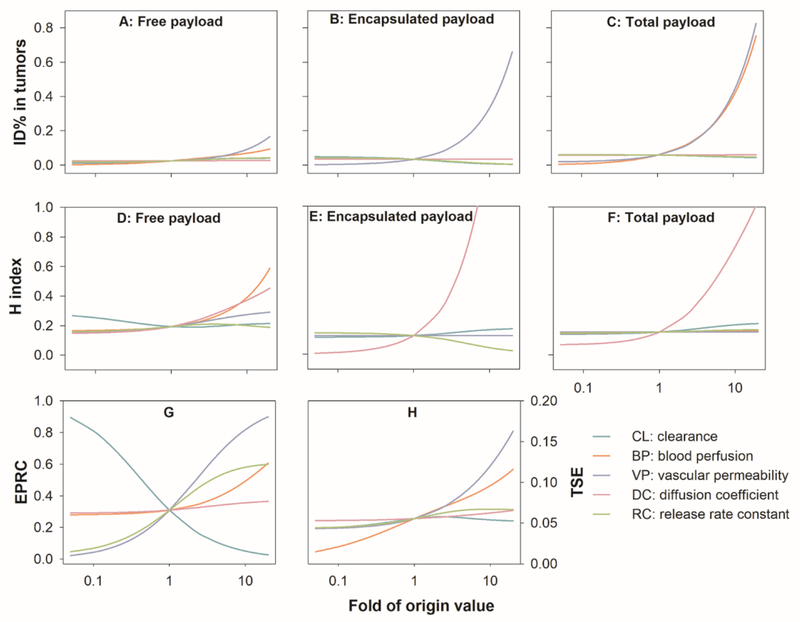
We assessed the influence of each individual factor listed in Table 1 on the ID%, H index, EPRC, and TSE. Figure 3 depicts the influence of each factor within an estimated 400-fold dynamic range in well-diffused tumor. As shown in Figure 3A–C, an increase in either nanoparticle VP or tumor BP considerably augmented nanoparticle tumor accumulation (encapsulated payloads). However, increased nanoparticle accumulation did not yield much of an increase in free payloads, and the free payload accumulation was only slightly affected by both factors.

Figure 3.

The influence of individual factors on (A-C) tumor delivery efficiency (ID%), (D-F) degree of heterogeneity (H index), (G) EPR contribution (EPRC), and (H) total tumor suppressive effect (TSE) in well-diffused tumor. Each factor was simulated within 0.05 ~ 20-fold of the values of Doxil. EPR: enhanced permeability and retention.

As shown in Figure 3D–F, the nanoparticle DC was the most effective factor in reducing the heterogeneous nanoparticle distribution in tumors. In contrast, the most effective factor in reducing the heterogeneous free payload distribution was tumor BP, where a 10-fold increase of BP resulted in a 0.2-unit increase of the H index (0.39 versus 0.19). While high tumor BP improved the spatial distribution of free payloads, it shortened the free payload retention in tumors. The free payload H index was not noticeably affected by any other tested factors, even though the nanoparticle H index significantly increased with a higher nanoparticle DC. The distributional heterogeneity of free payloads appears to be influenced by different factors than those that affect the distributional heterogeneity of nanoparticles. Consequently, commonly adopted strategies that merely attempt to improve nanoparticle spatial distribution (e.g., nanoparticle properties modification) may not necessarily result in improved free payload tumor distribution.

Tumor extracellular condition appeared as another factor that noticeably affected the heterogeneous nanoparticle and free payload distribution (Figure 3D–F, Figure S1D–F and S2D–F). The nanoparticle and free payload H indexes decreased 130-times and 40-times in poorly-diffused tumors compared to the well-diffused tumors. In poorly-diffused tumors, both nanoparticle and free doxorubicin DCs were significantly reduced. As nanoparticle DC has limited influence on the free payload H index in poorly-diffused condition, the reduced diffusion of free payload should result in high free payload H index in poorly-diffused condition. The radius ratio of intermediate to proximal layer was identified as a good predictor of the heterogeneous nanoparticle and free payload distribution (Figure S3).

As shown in Figure 3G, the EPRC was significantly affected by the nanoparticle CL, particle VP, and the nanoparticle RC inside tumors. Lowering the nanoparticle CL resulted in a substantial EPRC increase. Once clearance was decreased to 10% of the original value, the free payload tumor accumulation that was directly related to the EPRC increased from 31% to 81%. A low systemic nanoparticle clearance (i.e., high plasma stability) would remarkably reduce the levels of free payload in circulation, constraining the direct diffusion of free payload from the circulation into the tumors. Thus, this EPRC increase was at the cost of reducing tumor free doxorubicin exposure (0.012 versus 0.024 of ID%). The increased particle VP and nanoparticle RC could improve both EPRC and tumor free doxorubicin exposure.

As shown in Figure 3H, other factors influenced either the free payload ID% (VP), the free payload H index (BP), or the EPRC (RC and BP). All the factors had an impact on the TSE. The order of influence magnitude was VP > BP > RC. Of note, this order is not consistent with the order of factors that are sensitively associated with the nanoparticle H index, particularly the nanoparticle DC. This factor has the strongest effect on the nanoparticle H index but only exhibits minimal influence on the anti-tumor effect. All these conclusions were consistent among the three simulated tumor diffusion conditions (Figure 3, S1 and S2).

The combined effects of influencing factors

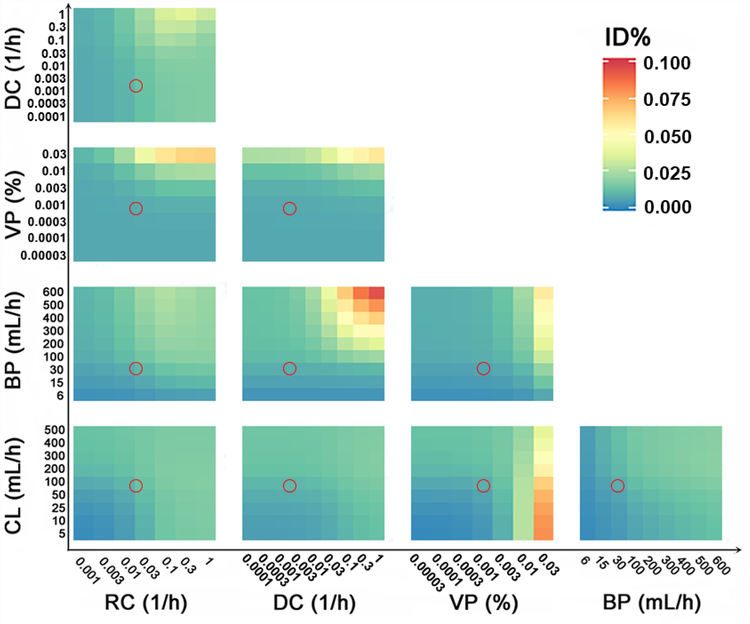
The effect of both factors optimized together (combined) was calculated based on an additive effect of the summed values of each of the single factors. The combined effects of the two factors on the free payload ID% are shown in Figure 4 for well-diffused tumor region. The greatest potential for free payload tumor accumulation was always associated with high nanoparticle VP, the only factor that was found to significantly affect free payload tumor delivery (Figure 3A). The factors that showed a significant combined effect with VP included tumor BP and nanoparticle RC. Of note, high free payload tumor accumulation only occurred when the VP was 10-fold higher than that for Doxil, a parameter that might not be practically feasible in breast cancer. However, the DC appeared as a more sensitive factor than nanoparticle VP in determining the free payload ID% in moderately- or poorly-diffused conditions (Figure S4 and S5).

Figure 4.

The combined effects of influencing factors (the effect by simultaneously changing two factors) on free payload tumor delivery efficiency (ID%) in well-diffused tumor. The colors represent the free payload ID%. The red circles represent Doxil in typical solid breast tumors. BP: tumor blood perfusion; CL: nanoparticle systemic clearance; DC: the nanoparticle diffusion coefficient in the tumor extracellular matrix; VP: nanoparticle vascular permeability; RC: the nanoparticle release constant in the tumor extracellular matrix.

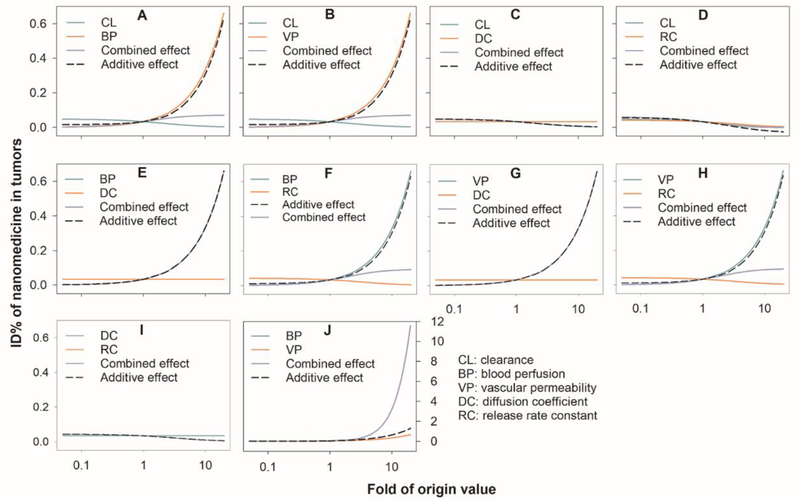
The combined effects of these factors on the nanoparticle ID% were also evaluated. The results are summarized in Figure 5 (well-diffused tumor), Figure S6 (moderately-diffused tumor) and Figure S7 (poorly-diffused tumor). As shown in Figure 5A–B, the benefits of tumor BP and particle VP to the nanoparticle ID% could be dramatically compromised by a relatively high nanoparticle CL. In line with the results shown in Figure 3B, the nanoparticle DC (Figure 5C) and the nanoparticle RC (Figure 5D) did not have much effect on the nanoparticle tumor accumulation. Neither factor had a noticeable combined effect with the nanoparticle CL on nanoparticle tumor accumulation; nor did they demonstrate any combined effect with the other two effective factors, BP and VP (Figures 5E–H). Notably, there was a strong synergistic effect between BP and VP (Figure 5I).

Figure 5.

Comparison of combined vs additive effects (the sum of the individual effects) on nanoparticle tumor delivery efficiency (ID%) in well-diffused tumor. BP: tumor blood perfusion; CL: nanoparticle systemic clearance; DC: the nanoparticle diffusion coefficient in the tumor extracellular matrix; VP: nanoparticle vascular permeability; RC: the nanoparticle release constant in the tumor extracellular matrix.

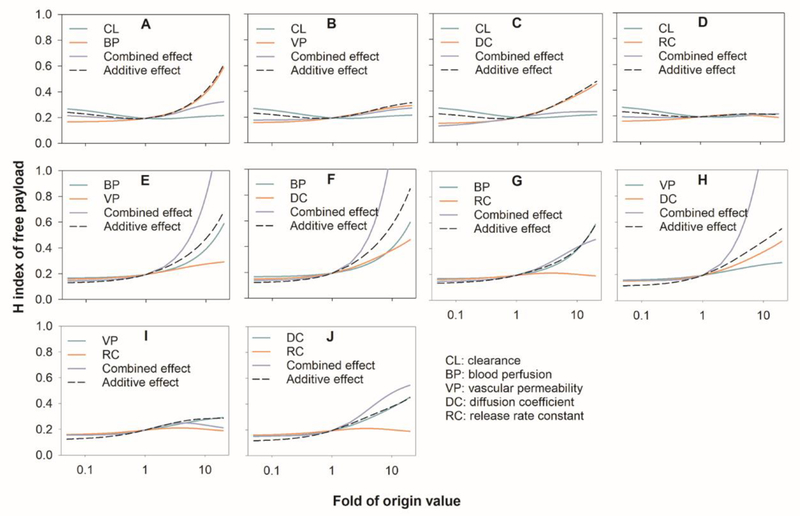
Figure 6 summarizes the combined effects on the free doxorubicin H index in well-diffused condition. Tumor BP was the most significant factor (Figure 3D) and exhibited a strong synergistic combined effect with nanoparticle DC and nanoparticle VP on the free doxorubicin H index. A highly synergistic combined effect was also observed between the nanoparticle DC and VP. There was no noticeable combined effect among the other factors. The combined effect on the free drug H index on different diffusion tumors is provided in the Supplement material (Figure S8 and S9). These data are consistent with the single factor results for nanoparticles (Figure 3).

Figure 6.

Comparison of the combined and additive effects (the sum of the individual effects) on the heterogeneous distribution (H index) of free payloads in tumors (well-diffused tumor). BP: tumor blood perfusion; CL: nanoparticle systemic clearance; DC: the nanoparticle diffusion coefficient in the tumor extracellular matrix; VP: nanoparticle vascular permeability; RC: the nanoparticle release constant in the tumor extracellular matrix.

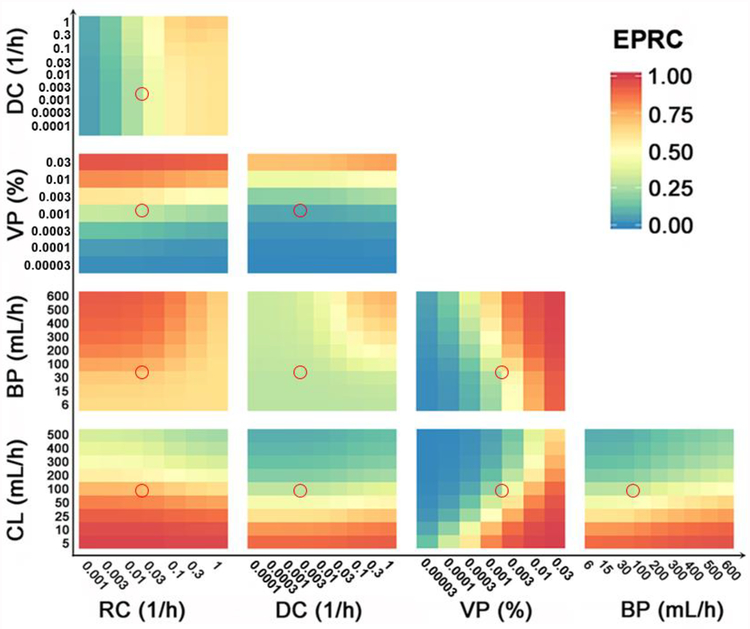
Figure 7, S10 and S11 depicts the combined effects on the EPRC in different tumor diffusion conditions. Three critical factors were found to be closely associated with the free payload ID%: nanoparticle CL, nanoparticle RC, and nanoparticle VP. These factors exhibited potent combined effects with each other. Only 2 to 3-fold adjustments of these factors would yield a significant EPRC enhancement. The combined effects of these factors on TSE are depicted in Figure S12 to S14. In line with the EPRC results, the factors that demonstrated significant single effects (Fig 3H) also had significant combined effects.

Figure 7.

The combined effects of the influencing factors on the EPR contribution (EPRC) to total tumor exposure of free payloads. The red circles represent Doxil in typical solid breast tumors (well-diffused tumor). The colors represent the free payload EPRC. BP: tumor blood perfusion; CL: nanoparticle systemic clearance; DC: the nanoparticle diffusion coefficient in the tumor extracellular matrix; VP: nanoparticle vascular permeability; RC: the nanoparticle release constant in the tumor extracellular matrix.

In summary, we found that the factors that significantly influenced free payload tumor accumulations (as reflected by ID%) and spatial distributions (as reflected by the H index) were not consistent with the influencing factors that were associated with nanoparticle disposition. The factors that were responsible for free doxorubicin disposition showed strong correlations with the factors that predicted overall anti-tumor efficacy (VP > BP > RC). Substantial synergistic combined effects were suggested between these factors.

Discussion

Tumor-targeted delivery has long been a central issue for cancer nanomedicines, but the theories underlying this topic have gradually evolved. The fundamental principle of the EPR effect has been challenged by its poor clinical translation. Previous efforts in nanomedicine research have focused almost entirely on extending nanomedicine’s systemic persistence and improving the concentration of the nanomedicines delivered into tumors. Intratumor distributional heterogeneity and its impact on the recent limited clinical benefits have become pivotal topics in nanomedicine research. Conventional methods used to evaluate the enhanced EPR effect are often based on the total quantity of nanoparticles delivered to tumors. However, nanoparticle tumor delivery is just the first step of the process, as intra-tumor free payload kinetics, interactions between free payloads and tumor cells, and heterogeneous free payload tumor distributions have become extremely important.

In this study, we developed a mathematical model to evaluate the heterogeneous distribution of nanomedicines in solid tumors. We applied this model to systematically compare many of the strategies that have been studied to either enhance the targeted delivery of nanomedicines or to improve the heterogeneous distribution of nanomedicines in solid tumors. Our analysis strongly supports the conclusion that the free payload distribution within tumors is fundamentally different from that of nanoparticles. Special attention should be paid to assessments of free payload disposition properties, as these are responsible for anti-tumor efficacy. We found that EPR-dependent nanoparticle delivery only contributed to a small fraction (~30% for Doxil) of the free payload tumor distribution. A large nanoparticle tumor delivery will not necessarily result in an effective free payload delivery. There is only a transient free payload increase from nanoparticles in the perivascular regions, and this increase will be quickly drained out into the circulation before it has a chance to diffuse into the distal tumor tissues, especially in poorly-diffused tumors. The factors that were found to significantly influence tumor free payload dispositions included tumor VP, tumor BP, and the nanoparticle RC into the tumor interstitial fluid. These factors also exhibited significant synergistic combined effects. These findings have valuable implications for cancer nanomedicines.

One key finding of our analysis was that free payload dispositional properties in tumors are significantly different from nanoparticles. Traditional approaches for evaluating the targeted delivery of nanomedicines largely hinge on nanoparticle measurements. However, nanoparticles are not directly bioavailable to tumor cells, and the tumor’s free payload exposure is responsible for anti-tumor efficacy. The measurement of tumor nanoparticle concentrations is therefore inadequate, and more effort should be focused on quantifying the tumor free payload concentrations. As indicated in Figure 3A–B, the tumor nanoparticle concentrations after nanomedicine administration are usually many times greater than an equivalent dose of traditionally-formulated doxorubicin, but the actual concentrations of free doxorubicin are much lower than that of the nanoparticles in the nanomedicine regimen. This is probably the major reason why FDA-approved liposomal drugs have failed to show superior patient survival benefits, even though the tumors accumulated high levels of nanoparticles.

While the EPR effect has traditionally been viewed as the foundational rationale for cancer nanomedicines, we found that the EPR effect contributed little to free payload tumor accumulation. As mentioned above, nanoparticle tumor delivery is just the first step of the process. The subsequent intratumor free payload distributions and the free payload interactions with the tumor cells are particularly important. As the free payload rapidly diffuses across the tumor vasculature once it is released from the perivascular nanoparticles, there is only a transient increase in free payload concentration in the perivascular interstitial space; the free payload will be quickly drained back into the blood circulation. Strategies that are designed to enhance nanoparticle tumor delivery may not be useful for increasing free payload tumor concentrations (Figure 4 versus Figure 5). This may be why a non-PEGylated product like Myocet, despite having a relatively shorter systemic persistence and different tumor accumulation levels than a PEGylated product like Doxil, exerts almost equivalent clinical efficacy with Doxil and the conventional free doxorubicin [2, 40].

Three factors were found to be critical for improving the overall anti-tumor effect: tumor VP, tumor BP, and nanoparticle RC in the tumor interstitial fluid. Significant synergistic effects were also suggested for the combinations of these factors. The normalization of disorganized and leaky blood vessels has been investigated as a mechanism for improving tumor BP and tumor VP. Anti-angiogenesis agents, such as anti-vascular endothelial growth factor (VEGF) monoclonal antibodies, have been used to address these permeability and perfusion issues. The anti-VEGF antibody bevacizumab has been shown to decrease IFP by 73% in rectal carcinoma, to enhance tumor vasculature and blood perfusion in non-small cell lung cancer, and to improve therapeutic efficacy when combined with carboplatin and abraxane [41]. Vascular normalization modalities should be studied in combination with nanomedicines to evaluate enhanced tumor delivery and therapeutic efficacy. The nanomedicine release rate is also a crucial factor identified in this study for enhanced free payload exposure in tumors. Tumor microenvironment-sensitive carriers have been developed to control nanomedicine release rates, including acid-triggered release, light-triggered release, and enzyme-triggered release [42–45]. These strategies can yield high free payload tumor concentrations and improved therapeutic efficacy [46].

The present study developed a mathematical framework to evaluate the heterogeneous distribution of nanomedicines in tumors. In this model, the heterogeneous distributions of nanoparticles and their free payloads were investigated. We found that the free payload spatial disposition in tumors was considerably different from that of nanoparticles. The factors that most influenced free payload distribution were different from those that affected nanoparticle distribution. EPR-dependent nanomedicine delivery provided only a limited contribution to the free payload tumor exposure. These findings highlight the importance of assessing free payload tumor distribution properties when assessing the efficacy of nanotherapeutics. The platform developed in this study provides a valuable tool for evaluating the heterogeneous distribution of nanomedicines and its effect on anti-tumor efficacy.

Abbreviations

BP

tumor blood perfusion

CL

nanoparticle systemic clearance

DC

the nanoparticle diffusion coefficient in the tumor extracellular matrix

EPR

enhanced permeability and retention

EPRC

EPR contribution

ID%

delivery efficiency, or the percentage of injected dose

H index

heterogeneity index

VP

nanoparticle vascular permeability

RC

the nanoparticle release constant in the tumor extracellular matrix

TSE

tumor suppressive effect