A stochastic model of ion channel cluster formation in the plasma membrane

Ion channels are often found in dense clusters within the plasma membranes of excitable cells. Based on experimental measurements of a wide range of channels in various cell types, Sato et al. propose that channel clusters form stochastically and that their size is regulated by a common feedback mechanism.

Abstract

Ion channels are often found arranged into dense clusters in the plasma membranes of excitable cells, but the mechanisms underlying the formation and maintenance of these functional aggregates are unknown. Here, we tested the hypothesis that channel clustering is the consequence of a stochastic self-assembly process and propose a model by which channel clusters are formed and regulated in size. Our hypothesis is based on statistical analyses of the size distributions of the channel clusters we measured in neurons, ventricular myocytes, arterial smooth muscle, and heterologous cells, which in all cases were described by exponential functions, indicative of a Poisson process (i.e., clusters form in a continuous, independent, and memory-less fashion). We were able to reproduce the observed cluster distributions of five different types of channels in the membrane of excitable and tsA-201 cells in simulations using a computer model in which channels are “delivered” to the membrane at randomly assigned locations. The model’s three parameters represent channel cluster nucleation, growth, and removal probabilities, the values of which were estimated based on our experimental measurements. We also determined the time course of cluster formation and membrane dwell time for Ca_V1.2 and TRPV4 channels expressed in tsA-201 cells to constrain our model. In addition, we elaborated a more complex version of our model that incorporated a self-regulating feedback mechanism to shape channel cluster formation. The strong inference we make from our results is that Ca_V1.2, Ca_V1.3, BK, and TRPV4 proteins are all randomly inserted into the plasma membranes of excitable cells and that they form homogeneous clusters that increase in size until they reach a steady state. Further, it appears likely that cluster size for a diverse set of membrane-bound proteins and a wide range of cell types is regulated by a common feedback mechanism.

Introduction

Cell biologists have been studying the mechanisms of ion channel expression and delivery to the membrane for decades. This work has revealed key roles for the cytoskeleton, channel subunits, scaffolding proteins, and/or lipid microdomains (e.g., caveolae) in the organization of ion channels in the plasma membrane (Shaw and Colecraft, 2013; Honigmann and Pralle, 2016; Goyette and Gaus, 2017; Ghosh et al., 2018; Krapf, 2018; Taylor et al., 2018). The process starts when messenger RNA encoding the transmembrane ion channel subunits is translated on ER-bound ribosomes from which the nascent polypeptides are translocated into the membrane. Fully assembled channel proteins leave the ER in vesicles that fuse with the trans-Golgi, where they undergo post-translation processing, including many ion channel subunits modification of N-linked glycosylation. These vesicles are transported as cargo by molecular motors traveling along microtubules that run from the cis side of the Golgi apparatus to the cytoplasmic surface (Newman et al., 2012; Ghosh et al., 2018). Ion channels appear on the cell surface upon fusion of these vesicles with the plasma membrane, which, depending on the ion channel and cell type, can occur at proximal sites or, in some cases, quite distant from where the vesicles emerged from the Golgi apparatus. Plasma membrane ion channels are eventually removed and either recycled or degraded via endocytic pathways.

The organization of ion channels has long been recognized to vary along a cell’s membranous surface (Catterall, 1981; Beam et al., 1985; Waxman and Ritchie, 1985; Block et al., 1988). Descriptions of the distributions of ion channels in the plasma membrane have been based on the analysis of electron micrographs (Waxman and Ritchie, 1985; Block et al., 1988; Takagishi et al., 1997; Gathercole et al., 2000; Duffin et al., 2009), confocal images of cells exposed to protein-specific antibodies attached to fluorescent moieties (Jorgensen et al., 1990), and, more recently, superresolution imaging (Baddeley et al., 2009; Mercado et al., 2014; Dixon et al., 2015; Moreno et al., 2016; Tajada et al., 2017; Vivas et al., 2017). In most instances, it has been shown that many ion channels aggregate into dense clusters. For example, in neurons, ligand-gated ion channel proteins involved in synaptic transmission are concentrated on the dendritic and somatic membranes (Kim et al., 1996), whereas the voltage-gated ion channels required for the release of neurotransmitter are restricted to the axon terminals (Catterall, 1981; Beam et al., 1985; Kim et al., 1995; Duffin et al., 2009). In striated muscle, dihydropyridine-sensitive voltage-gated Ca²⁺ channels form clusters along the sarcolemma and transverse tubules of the cells (Block et al., 1988; Gathercole et al., 2000). Such exquisite spatial arrangements of ion channels are critical for efficient biological functions in both neurons and muscle. Indeed, clustering of voltage-gated Ca²⁺ channels is critical for the amplification of Ca²⁺ influx that is necessary to initiate neurotransmitter release in neuronal terminals and to sustain excitation–contraction coupling in muscle. Furthermore, it has recently been demonstrated that proteins engaged in cooperative signaling cascades display co-clustering. For example, clusters of large-conductance Ca²⁺-activated K⁺ (BK) channels are surrounded by clusters of Ca_V1.3 channels that generate the requisite local Ca²⁺ influx (Cox, 2014; Vivas et al., 2017). Despite these advances, a broadly applicable quantitative model that amalgamates key concepts of ion channel insertion and organization in mammalian cells is lacking.

We gain some insight on the mechanisms underlying channel cluster formation from studies performed in bacteria, where time-lapse fluorescence images suggest that chemoreceptor proteins are inserted randomly into the membrane via the general protein translocation machinery of the cells and then diffuse to existing clusters (Shiomi et al., 2006). The distance between clusters, however, varied widely within cells, prompting Thiem et al. (2007) to propose that protein cluster formation and growth is a stochastic self-assembly process in which newly synthesized proteins diffuse in the membrane and then join existing clusters or create new clusters. In their model, clusters can originate anywhere in the membrane and later become attached to scaffolding or anchoring sites. Shortly thereafter, it was reported that anchoring sites may not be required for the formation of new clusters, and their simulations suggested that the periodic positioning of new clusters can emerge spontaneously in growing cells (Wang et al., 2008). At present, however, it is unclear whether the distribution of ion channels in the surface membrane of mammalian cells could be the result of a similar stochastic self-assembly process of protein organization.

In the work described here, we used superresolution fluorescent microscopy to determine the sizes and densities of clusters of five different ion channel proteins expressed in the surface membranes of ventricular myocytes (Ca_V1.2), smooth muscle cells (Ca_V1.2, TRPV4, and BK channels), neurons (Ca_V1.3), and tsA-201 cells (Ca_V1.2, Ca_V1.3_S, Ca_V1.3_L, and TRPV4 channels). We found that the probability density functions of the cluster sizes of all of these ion channels could be fit with an exponential function, a hallmark of a Poisson process. Thus, we generated a mathematical model in which vesicles containing ion channel proteins are inserted into the membrane at random locations. The model reproduced the observed steady-state clustering of Ca_V1.2, Ca_V1.3, TRPV4, and BK channels in the membranes of neurons, cardiomyocytes, smooth muscle, and tsA-201 cells. To further elaborate and constrain our model, we studied the formation and growth of clusters of Ca_V1.2 and TRPV4 channels expressed in tsA-201 cells, as well as the turnover rate of these channels in the membrane. We found that adding a regulatory feedback mechanism scaled to channel number enhanced its capacity of the model to reproduce our experimental observations. On the basis of our experimental and modeling results, we propose that the regulation of cluster size for both a diverse set of membrane-bound proteins and a wide range of cell types is regulated by a common feedback mechanism. Our model constitutes a novel tool for identifying potential mechanisms by which specific proteins and signaling pathways could dynamically shape membrane channel cluster formation.

Materials and methods

Immunofluorescence and superresolution microscopy

We performed immunofluorescence and superresolution imaging experiments using methods similar to those described elsewhere (Mercado et al., 2014; Dixon et al., 2015; Moreno et al., 2016; Tajada et al., 2017; Vivas et al., 2017). Briefly, cells were fixed at the specified times after transfection by incubating in PBS containing 3% paraformaldehyde and 0.1% glutaraldehyde for 10 min at room temperature. After washing with PBS, cells were incubated with sodium borohydride (1 mg/ml) for 10 min at room temperature, washed again with PBS, and blocked by incubating in 3% bovine serum albumin and 0.25% vol/vol Triton X-100 in PBS for 1 h at room temperature (≈20°C). The cells were incubated either overnight at 4°C or for 1 h at room temperature with anti-GFP antibody conjugated to Alexa Fluor 647 (A-31852; Thermo Fisher) diluted in blocking buffer to a concentration of 10 µg/ml. After washing with PBS, samples were postfixed with 0.25% glutaraldehyde in PBS for 10 min at room temperature, washed with PBS, and prepared for imaging.

Coverslips were mounted on microscope slides with a round-bottom cavity (NeoLab Migge Laborbedarf-Vertriebs) using fresh cysteamine–glucose oxidase (MEA-GLOX) imaging buffer. The day of the experiment, a stock of 5 ml of 100 mM MEA (cysteamine hydrochloride, M6500; Sigma-Aldrich) in PBS was prepared and pH was adjusted to 8.2 with potassium hydroxide (KOH), 10M. A stock of GLOX containing 50 µl of 10 mM Tris-HCl, pH 8, 3.5 mg glucose oxidase (G2133; Sigma-Aldrich), and 12.5 µl catalase (C100; Sigma-Aldrich) was prepared, sonicated for 5 min, and centrifuged for 3 min at 13,000 rpm at 4°C. This stock was kept at 4°C and used within 1 wk. Finally, 50 ml of Buffer B, containing 200 mM Tris-HCl, pH 8, 10 mM NaCl, and 10% wt/vol glucose, was prepared, kept at 4°C, and used within 6 mo. Right before mounting the coverslip, the final MEA-GLOX buffer was mixed by adding a ratio of 89:10:1 of Buffer B/MEA/GLOX. The final concentration of the components in this imaging buffer was 10 mM MEA, 0.56 mg/ml glucose oxidase, and 34 µg/ml catalase. Coverslips were sealed with Twinsil (Picodent) and aluminum tape to reduce oxygen permeation.

Superresolution images were generated using a superresolution ground-state depletion system (Leica) equipped with high-power lasers (488 nm, 1.4 kW/cm²; 532 nm, 2.1 kW/cm²; and 642 nm, 2.1 kW/cm²) and an additional 30-mW, 405-nm laser. Images were obtained using a 160× HCX Plan-Apochromat (numerical aperture 1.43) oil-immersion lens and an electron multiplying charge-coupled device camera (iXon3 897; Andor Technology). For all experiments, the camera was running in frame-transfer mode at a frame rate of 100 Hz. Fluorescence was detected through Leica high-power TIRF filter cubes (488 HP-T, 532 HP-T, and 642 HP-T) with emission band-pass filters of 505–605 nm, 550–650 nm, and 660–760 nm.

Superresolution localization images were reconstructed using the coordinates of centroids obtained by fitting single-molecule fluorescence signals with a 2-D Gaussian function using Leica Application Suite Advanced Fluorescence software (Leica). A total of 35,000 images were used to construct the images. The localization accuracy of the system is limited by the statistical noise of photon counting. Thus, assuming the point-spread functions are Gaussian, the precision of localization is proportional to DLR/√N, where DLR is the diffraction-limited resolution of a fluorophore and N is the average number of detected photons per switching event (Fölling et al., 2008; Dempsey et al., 2011). Accordingly, we estimated a lateral localization accuracy of 16 nm for Alexa Fluor 647 (≈1,900 detected photons per switching cycle).

For this paper, we reanalyzed previously published superresolution images of Ca_V1.2 channels from ventricular myocytes (Dixon et al., 2015) as well as Ca_V1.3 channels from hippocampal neurons and tsA-201 cells (Moreno et al., 2016) and TRPV4 channels from arterial smooth muscle cells (Mercado et al., 2014; Tajada et al., 2017). The figure legends in the present report differentiate data derived from those studies versus data derived from new experiments. Detailed experimental procedures on the treatment and imaging of the reanalyzed cells can be found in the original papers cited above.

tsA-201 cell transfection

tsA-201 cells (Sigma-Aldrich) were cultured in Dulbecco’s modified Eagle medium (Gibco) supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin at 37°C in a humidified 5% CO₂ atmosphere. Cells were plated onto 25-mm round 1.5 coverslips and transiently transfected using jetPEI (Polyplus Transfection). For the Ca_V1.2 experiments, cells were transfected with plasmids encoding the rabbit Ca_V1.2 (α_1C) conjugated to EGFP (600 ng) and rat auxiliary subunits Ca_Vα₂δ (300 ng) and Ca_Vβ₃ (600 ng; kindly provided by Dr. Diane Lipscombe; Brown University, Providence, RI). For the TRPV4 experiments, cells were transfected with 600 ng of a plasmid encoding the mouse TRPV4-EGFP (kindly provided by Dr. Philipp Slusallek, Saarland University, Saarbrücken, Germany) in which the GFP moiety has been mutated to prevent oligomerizarion. For photoactivation experiments, cells were transfected with Ca_V1.2 tagged at their C terminus with photoactivatable GFP (600 ng; GenScript) and auxiliary subunits stated above or TRPV4 tagged at their C terminus with photoactivatable GFP (600 ng; GenScript).

Time-lapse confocal microscopy

The live-cell imaging of photoactivatable experiments were performed on an Olympus Fluoview 3000 (FV3000) confocal laser-scanning microscope equipped with an Olympus Plan-Apochromat 60×/1.40 numerical aperture oil-immersion objective. We used 405-nm laser light to photoactivate the photoactivatable-Ca_V1.2 and photoactivatable-TRPV4 channels. Pre-stimulation images were collected in order to normalize fluorescence signal. Upon excitation, robust GFP fluorescence emission was observed. Normalized fluorescence time courses were compiled by averaging line scans of various regions of interest (ROIs) from each cell. ROIs were resliced and quantified over time.

Stochastic self-assembly model

To simulate the aggregation process of channels within cell membranes, we developed a simplified stochastic self-assembly model of cluster growth modified from stochastic self-assembly algorithms proposed for bacterial proteins and ryanodine receptors (Wang et al., 2008; Baddeley et al., 2009; Greenfield et al., 2009). As was done by Baddeley et al. (2009) for ryanodine receptors, our model does not consider channel diffusion for cluster formation. The observation that voltage-gated Na⁺ channels in the sarcolemma of skeletal muscle fibers are immobile suggests that lateral channel diffusion, at least in native muscle cells, may not be a significant determinant of cluster growth (Stühmer and Almers, 1982).

In our model, the cell membrane is represented by a 10 × 10 µm virtual 2-D square grid $(Gri{d}_{ij})$. This space is subdivided into 10⁶ “grid sites,” each of which measures 10 × 10 nm and represents the space that can be occupied by an individual ion channel molecule. Particles simulating ion channels were inserted randomly into the grid with cluster growth and density determined by three model parameters representing nucleation (P_n), growth (P_g), and removal (P_R) probabilities.

We first assume that at time t = 0, there are no channels present in the grid ($Gri{d}_{ij}=0$). Then, in each iteration, there are three processes: (1) nucleation, (2) cluster growth, and (3) removal.

Nucleation

For nucleation, channels are inserted into the grid randomly with nucleation probability $P_n$ at each time step (Fig. S1 A). In this study, each iteration is equal to 18 s.

Cluster growth

If a grid site becomes occupied by a channel ($Gri{d}_{ij}=1$), cluster growth is induced:

$$Gri{d}_{ij}=\{\begin{array}{c}1, occupied\\ 0, empty \end{array}.$$

For simplicity, cluster growth is simulated by random insertion of a channel in any one of the four available grid sites immediately adjacent to a nucleating channel with growth probability $P_g$ at each time step (Fig. S1 B). Once one channel is added to the existing nucleating channel, a cluster is formed. After that, the growth probability of a cluster is P_g × the number of available neighbors.

Removal of clusters

Concurrently with growth, in each time step, there is a removal probability, $P_R$, for clusters already formed on the grid. It is important to note that we have defined a cluster to be a group of two or more channels. Clusters dwell in the membrane for some time before they are recycled or degraded. Therefore, the removal probability, P_R, of a cluster increases depending on its size (P_R × the number of channels; Fig. S1 C). Because clusters will grow until they are recycled or degraded, the removal probability sets a limit for maximal cluster size.

The parameters P_n, P_g, and P_R were specified using two methods. In the first, we defined probabilities P_n (t), P_g (t), and P_R (t). The probabilities P_g (t) and P_n (t) were defined to be sigmoid functions based on a correlation between the experimental fitting of mean cluster area and density and P_g and P_n, respectively. In addition, P_R was defined to be an increasing sigmoid function to account for the observation that Ca_V1.2 channel internalization increases as the number of channels increases (Green et al., 2007). These parameters were based on the experimental data using the time course of the distribution of cluster sizes, and the values were determined by a nonlinear least-squares method (Figs. 3 and 4 and Table 1).

Figure 3.

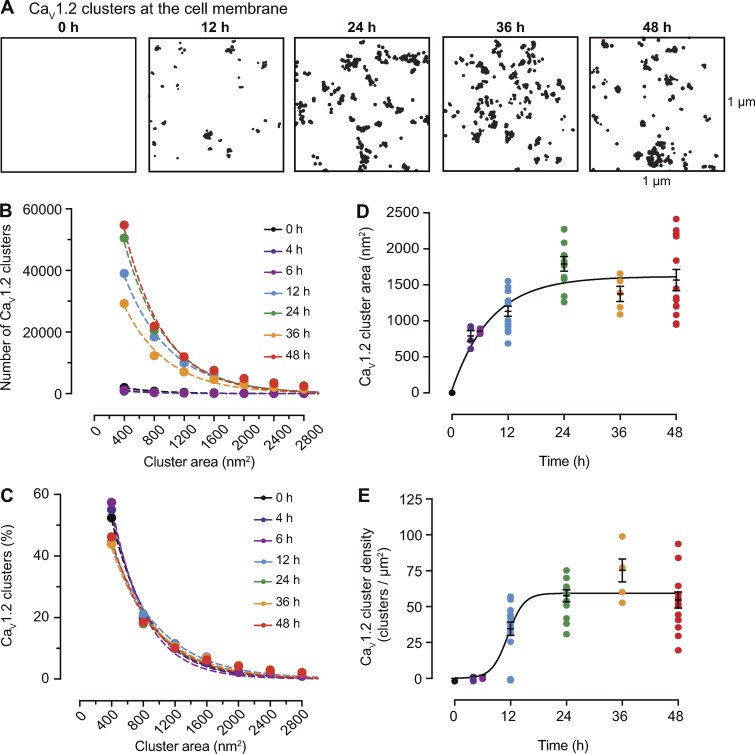
Time course of the formation of Ca_V1.2 channel clusters in tsA-201 cells. (A) Representative superresolution GSD binary masks of immunolabeled Ca_V1.2 channels expressed in tsA-201 cells at 0, 12, 24, 36, and 48 h after transfection. (B) Frequency distribution of Ca_V1.2 channels cluster areas at each time point. (C) Relative frequency distribution of Ca_V1.2 channels cluster areas expressed as percentages. Dashed color lines in B and C represent the best single exponential decay function fit for each dataset. (D) Change of mean Ca_V1.2 channel cluster area at different time points after transfection. Data are presented as mean ± SEM for individual cells at each time point. Mean cluster area data were fit with a one-phase exponential equation (solid black line). The tau value of the fit is 8.37 h. (E) Change of Ca_V1.2 channel cluster density at different time points after transfection. Data are presented as mean ± SEM for individual cells at each time point. Mean cluster density data were fit with a sigmoidal function (solid black line). The logIC₅₀ fit is 11.42 h. (B–E) All data were compiled as follows: 4 h: n = 1,497 clusters from 4 cells; 6 h: n = 2,100 clusters from 4 cells; 12 h: n = 87,209 clusters from 16 cells; 24 h: n = 114,805 clusters from 11 cells; 36 h: n = 66,769 clusters from 5 cells; 48 h: n = 118,281 clusters from 13 cells.

Figure 4.

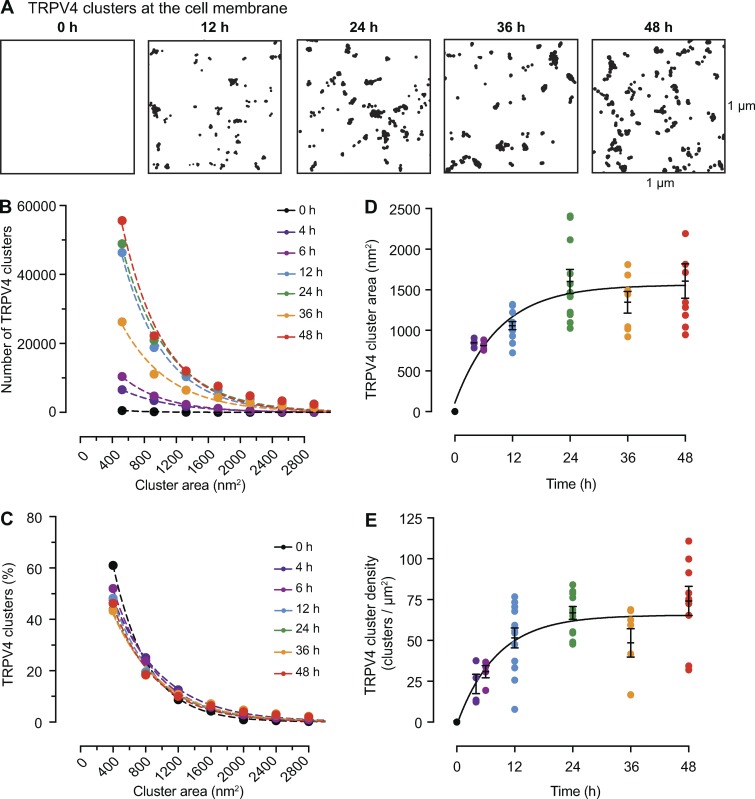
Time course of the formation of TRPV4 channel clusters in tsA-201 cells. (A) Representative superresolution GSD binary masks of immunolabeled TRPV4 channels in transfected tsA-201 cells at 0, 12, 24, 36, and 48 h after transfection. (B) Frequency distribution of TRPV4 channels cluster areas at each time point. (C) Relative frequency distribution of TRPV4 channels cluster areas expressed as percentages. Dashed color lines in B and C represent the best single exponential decay function fit for each dataset. (D) Change of mean TRPV4 channel cluster area at different time points after transfection. Data are presented as mean ± SEM for individual cells at each time point. (E) Change of TRPV4 channel cluster density at different time points after transfection. Data are presented as mean ± SEM for individual cells at each time point. Mean cluster area data (D) and mean cluster density data (E) were fit with a one-phase exponential equation (solid black line). The tau values for cluster area and cluster density are 9.17 and 8.22 h, respectively. (B–E) All data were compiled as follows: 4 h: n = 13,734 from 4 cells; 6 h: 20,004 clusters from 4 cells; 12 h: n = 96,295 clusters from 12 cells; 24 h: n = 111,632 clusters from 11 cells; 36 h: n = 60,518 clusters from 7 cells, 48 h: n = 120,416 from 12 cells.

Table 1. Feedback model parameters and initial conditions.

	Kn	Kg	KR	rn	rg	rR	InitialPn	InitialPg	InitialPR
CaV1.2	0.00045	0.07	0.001166667	0.000002	0.0018	0.0003	0.000000225	0.004375	0.00019444
TRPV4	0.00045	0.07	0.001166667	0.000002	0.0005	0.0003	0.000005921	0.004375	0.00010606

In our second method, the parameters P_n, P_g, and P_R have a feedback mechanism. In this feedback model, Ca_V1.2 and TRPV4 expressions are regulated by the number of channels. In this study, P_n, P_g, and P_R linearly increase or decrease until they reach steady-state values. Then, the basic feedback model is described by the following differential equations,

$$\frac{d{P}_n}{dt}=r_{n}N\left(1-\frac{P_n}{K_n}\right), (1)$$

$$\frac{d{P}_g}{dt}=r_{g}N\left(1-\frac{P_g}{K_g}\right), (2)$$

$$\frac{d{P}_R}{dt}=r_{R}N\left(1-\frac{P_R}{K_R}\right), (3)$$

where r_n, r_g, and r_R are growth rates of P_n, P_g, and P_R, respectively, K_n, K_g, and K_R are steady-state values of P_n, P_g, and P_R, respectively, and N is the number of channels per unit area.

Online supplemental material

Fig. S1 describes how our stochastic self-assembly model works. Video 1 depicts how our model simulates the nucleation, growth, and removal of clusters. Video 2 shows the effects of varied P_g and P_r values on channel and cluster dwell times. Videos 3 and 4 show the time courses of P_n, P_g, and P_R as well as simulated clusters for Ca_V1.2 and TRPV4 channels using the feedback model. These videos also depict the time courses of cluster area and density growth.

Results

The distributions of Ca_V1.2, Ca_V1.3, BK, and TRPV4 channel cluster sizes are fit by an exponential function

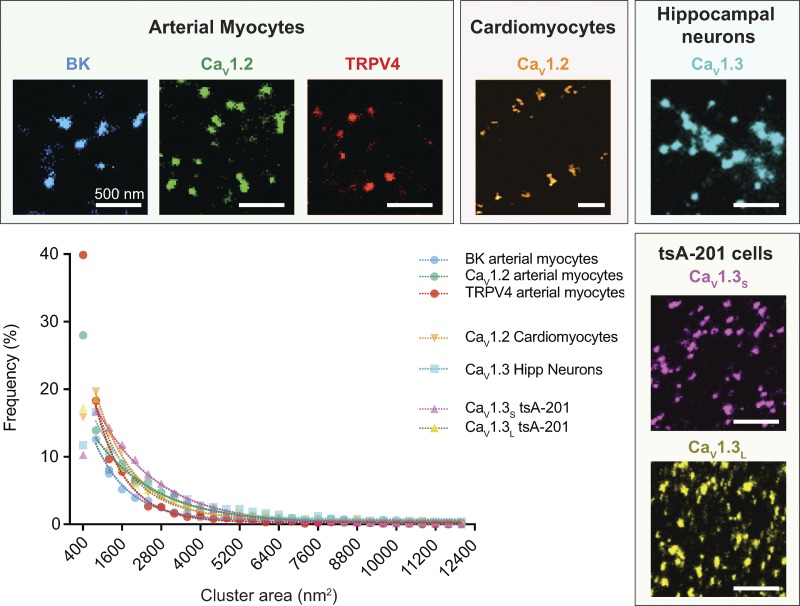
Over the last five years, our research team has been using superresolution imaging to determine the spatial organization of Ca²⁺-permeable and Ca²⁺-sensitive ion channels in the surface membrane of multiple cell types. In this paper, we have reanalyzed our previously published superresolution data on Ca_V1.2 channels in cardiomyocytes (Dixon et al., 2015), two isoforms of the Ca_V1.3 channel in hippocampal neurons and heterologous cells (Moreno et al., 2016), and TRPV4 channels in arterial myocytes (Tajada et al., 2017) to provide a broad, quantitative examination of how different types of channels are organized in the plasma membrane with nanometer resolution. To this extensive dataset, we have added new, equivalent measurements on Ca_V1.2 channels and the BK channels in the sarcolemma of arterial myocytes. As was the case in our prior analyses, we found that the Ca_V1.2 channels were expressed into dense clusters of different size along the surface membrane with a mean cluster area 2,488 ± 140 nm², similar to what we found in ventricular myocytes (2,555 ± 82 nm²; Dixon et al., 2015; Table 2). The BK channels also formed clusters along the sarcolemma of the arterial myocytes with a mean cluster area of 3,008 ± 223 nm².

Table 2. Summary of experimental superresolution data.

Ion channel	Cluster area (nm2)	Cluster density (clusters/µm2)
Smooth muscle
CaV1.2	2,488 ± 140	9.7 ± 0.4
TRPV4	1,834 ± 117	7.8 ± 0.2
BK	3,008 ± 223	9.2 ± 0.5
Cardiac muscle
CaV1.2	2,555 ± 82	21.9 ± 1.5
Hippocampal neurons
CaV1.3	3,660 ± 80	23.3 ± 1.8
tsA-201 cellsa
CaV1.2	1,566 ± 148	54.6 ± 5.7
CaV1.3S	2,119 ± 73	15.8 ± 4.3
CaV1.3L	2,543 ± 50	14.9 ± 4.3
TRPV4	1,605 ± 212	73.4 ± 8.9

^a48 h after transfection.

Fig. 1 displays samples of the superresolution images we have generated for five different channel proteins (BK, Ca_V1.2, TRPV4, Ca_V1.3_S, and Ca_V1.3_L) in four different kinds of cell membranes (arterial myocytes, cardiomyocytes, hippocampal neurons, and tsA-201 cells). In each case, we found that the channels are arranged into dense clusters with a wide range of sizes throughout the cell membranes. In the same figure, we have plotted the frequency distributions of cluster sizes for each of our datasets that remarkably reveal that each can be fit by a single exponential function.

Figure 1.

BK, Ca_V1.2, TRPV4, and Ca_V1.3 channels organize in clusters in multiple cell types exhibiting an exponential cluster area distribution. Representative superresolution ground state depletion images of the cluster organization of endogenous BK (blue), Ca_V1.2 (green), and TRPV4 (red) channels in arterial myocytes, endogenous Ca_V1.2 (orange) channels in cardiomyocytes, endogenous Ca_V1.3 (light blue) channels in hippocampal neurons, and the two splicing variants Ca_V1.3_S (pink) and Ca_V1.3_L (yellow) expressed in tsA-201 cells. The plot summarizes the frequency distribution of the cluster areas for each channel. All the distributions were fit with a single exponential function. Average cluster areas and densities for each channel are presented in Table 2. TRPV4 data were modified from Tajada et al. (2017), Ca_V1.2 in cardiomyocytes was modified from Dixon et al. (2015), and Ca_V1.3 data were modified from Moreno et al. (2016).

Stochastic self-assembly may account for the formation of homogeneous clusters of membrane channels in neurons, cardiomyocytes, and smooth muscle cells

Our finding that the size distributions of clusters for five different channel proteins could all be described by exponential functions, the hallmark of a Poisson process, strongly suggested that the clusters are formed stochastically in a continuous, independent, and memory-less fashion. A similar proposal was advanced by Wang et al. (2008) and Greenfield et al. (2009) to account for the spatial organization of chemotactic proteins in bacterial membranes and by Baddeley et al. (2009) for ryanodine receptors in ventricular myocytes. To test our hypothesis, we modified the approach employed by Baddeley et al. (2009) to create a new model to reproduce our cluster distributions and make testable predictions regarding plasma membrane protein organization.

Our modeling begins with the generation of a 10 × 10 µm grid composed of 10⁶ pixels. The dimension of each pixel (100 nm²) in this grid is similar to the size of individual Ca_V1 (Wu et al., 2015) and TRPV4 channels (Shigematsu et al., 2010; Deng et al., 2018). Particles simulating ion channels were inserted randomly into the grid with cluster growth and density determined by three model parameters representing nucleation (P_n), growth (P_g), and cluster removal (P_R). These parameters are probability functions meant to represent different biological processes. P_n is the probability that a vesicle containing an ion channel (or channels) will be randomly inserted at any site in the membrane. Nucleation is the first step in the formation of a new structure via self-assembly or self-organization. In our model, P_n values are uniform across the grid. At the beginning of the simulation, most “seeding” events involve the insertion of single channels. However, once cluster growth has initiated, the model allows for the stochastic insertion of multiple channels at any particular site. P_g is the probability of a channel to be inserted immediately adjacent to pre-existing channels. In our model, cluster growth is simulated by random insertion of a channel in any one of the four available grid sites immediately adjacent to a nucleating channel. The growth probability of a cluster is P_g × the number of available neighbors. Once a channel or small cluster is “seeded” in the membrane, the probability of insertion of a new channel adjacent to it increases, inducing cluster growth. The final parameter, P_R, represents the probability of a channel or cluster of channels being removed from the membrane by endocytosis and/or degradation. Individual channels and clusters were randomly removed every iteration. Video 1 illustrates how our model simulates cluster nucleation, growth, and removal.

The key question was whether this simple model could reproduce the cluster area distributions we measured from our superresolution images of endogenous channels in arterial myocytes, cardiomyocytes, hippocampal neurons, and channels expressed exogenously in tsA-201 cells. Because we could not observe the formation of the channel clusters as the cells develop, we assumed that the cluster area and density distributions we measured represented steady-state conditions and set the parameters P_n, P_g, and P_R to constant values.

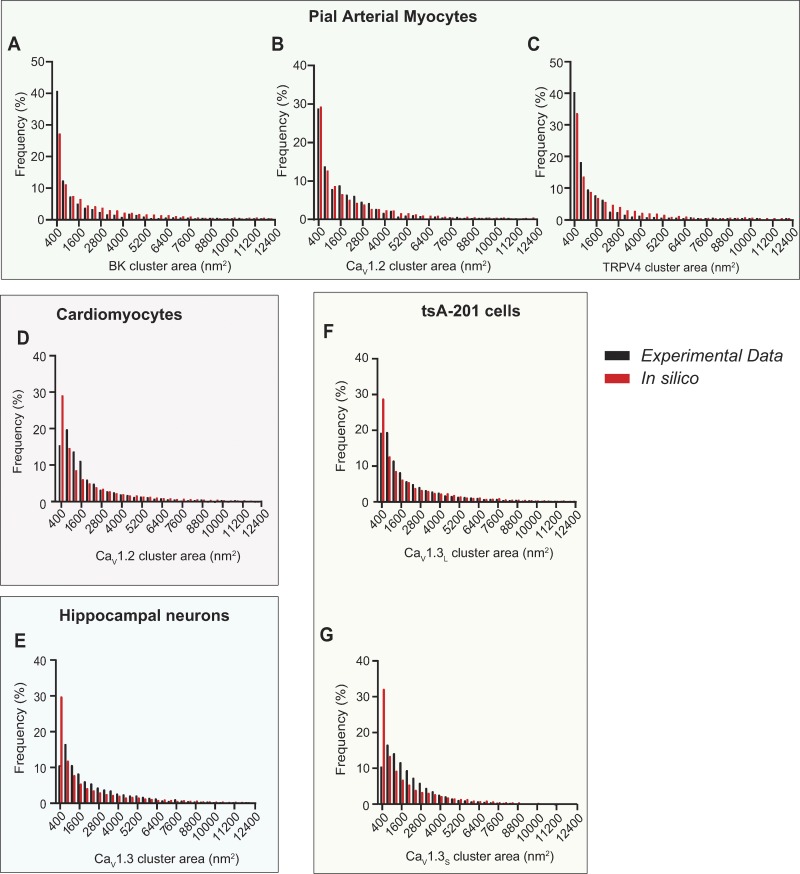
As shown in Fig. 2, our stochastic self-assembly model effectively reproduced the steady-state size distributions and mean cluster areas that we measured for all five channels proteins embedded in the membrane of four different cell types: arterial myocyte BK channels (Fig. 2 A), arterial myocyte Ca_V1.2 channels (Fig. 2 B), arterial myocyte TRPV4 channels (Fig. 2 C), ventricular myocyte Ca_V1.2 channels (Fig. 2 D), neuronal Ca_V1.3 channels (Fig. 2 E), tsA-201 Ca_V1.3_L channels (Fig. 2 F), and tsA-201 Ca_V1.3_S channels (Fig. 2 G). All the parameters used in these simulations are shown in Table 3.

Figure 2.

The distributions of Ca_V1.2, TRPV4, and BK channels in smooth muscle, Ca_V1.2 in ventricular myocytes, and Ca_V1.3 in neurons and tsA-201 cells could be explained by a stochastic self assembly of clusters. Histograms of the experimental (black bars) and simulated (red bars) clusters area distributions of (A) BK, (B) Ca_V1.2, and (C) TRPV4 channels in arterial myocytes, (D) Ca_V1.2 in ventricular myocytes, (E) Ca_V1.3 channels in hippocampal neurons, and (F) Ca_V1.3_L and (G) Ca_V1.3_S channels in tsA-201 cells.

Table 3. Summary of in silico steady-state data.

Ion channel	Cluster area (nm2)		Cluster density (clusters/µm2)		Steady-state Pg, PR, Pn
	Short dwell time	Long dwell time	Short dwell time	Long dwell time	Short dwell time	Long dwell time
Smooth muscle
CaV1.2	2,481	2,479	9.7	9.7	Pg = 0.1	Pg = 0.01
					PR = 0.0012803	PR = 0.0001609
					Pn = 0.000043648	Pn = 0.00000519639
TRPV4	1,819	1,851	7.8	7.8	Pg = 0.1	Pg = 0.01
					PR = 0.0020398	PR = 0.00027071
					Pn = 0.000039526	Pn =0.000004824
BK	2,981	3,030	9.2	9.24	Pg = 0.1	Pg = 0.01
					PR = 0.00097263	PR = 0.000119
					Pn = 0.000036651	Pn = 0.000004355
Cardiac muscle
CaV1.2	2,559	2,543	21.9	21.8	Pg = 0.1	Pg = 0.01
					PR = 0.0010796	PR = 0.00013367
					Pn = 0.00011952	Pn = 0.000014258
Hippocampal neurons
CaV1.3	3,657	3,697	23.2	23.4	Pg = 0.1	Pg = 0.01
					PR = 0.00052117	PR = 0.00006295399
					Pn = 0.0001249	Pn = 0.000014666
tsA-201 cells
CaV1.3S	2,103	2,127	17.1	15.8	Pg = 0.05	Pg = 0.005
					PR = 0.00086217	PR = 0.00010066
					Pn = 0.000044351	Pn = 0.00000476312
CaV1.3L	2,539	2,558	14.8	15.0	Pg = 0.05	Pg = 0.005
					PR = 0.00058827	PR = 0.0000787855
					Pn = 0.000036252	Pn = 0.0000042249

Time-dependent assembly of Ca_V1.2 and TRPV4 channel clusters

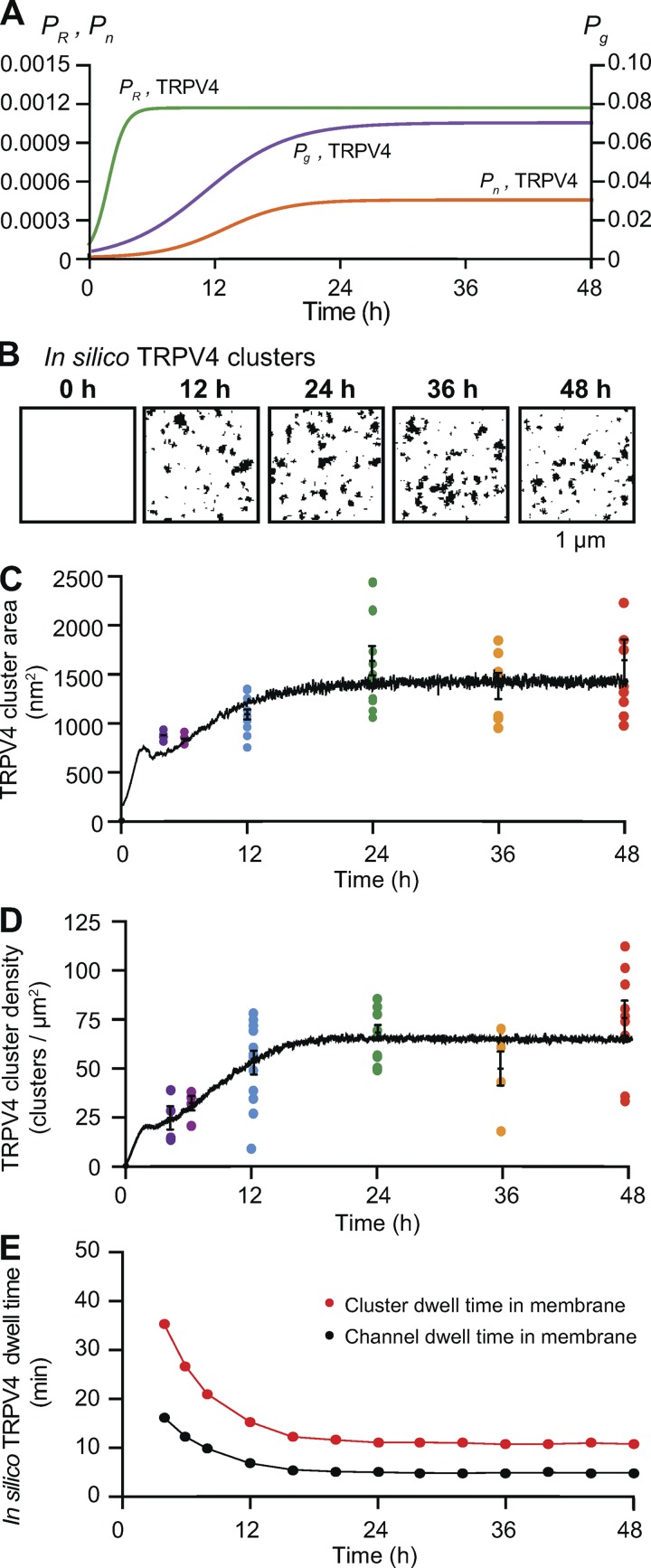
As mentioned above, the superresolution images from which we measured channel cluster sizes and densities present only a snapshot of the cell membrane. We had no information as to how the channel clusters develop and are maintained over time. To address this issue, we expressed Ca_V1.2-EGFP (Fig. 3) or TRPV4-EGFP channels (Fig. 4) in tsA-201 cells, fixed the cells at 0, 4, 6, 12, 24, 36, and 48 h after transfection, immunolabeled the channels, and acquired superresolution images of the channels in the membrane. These images permitted us to determine how the distribution of channel cluster sizes changed over a 48-h period. In Fig. 3 A, we show superresolution images of a tsA-201 cell at different time points following transfection with the Ca_V1.2-EGFP plasmid. The images were analyzed to quantify the area and densities of the Ca_V1.2 channel clusters (Fig. 3, B–E). The frequency histograms of cluster areas were generated from the images acquired at each time point. This analysis revealed that although the number of clusters varied with time, the size distributions could all be fit with single exponential functions that differed mainly in their amplitude (Fig. 3 B). Accordingly, histograms generated using the percentage of total clusters within each bin of cluster area were similar (Fig. 3 C). These data reveal that the mean size of the Ca_V1.2 clusters within the population of tsA-201 cells increased rapidly over the first 12 h after transfection and then reached a plateau at ∼24 h (Fig. 3 D). These data could be fit with exponential functions with a half-amplitude (T_1/2) at 5.8 h after transfection. Ca_V1.2 cluster density, like mean cluster area, also reached a plateau by ∼24 h and could be fit with a sigmoidal function with a T_1/2 at 11.5 h (Fig. 3 E).

In Fig. 4 A, we show superresolution images of representative tsA-201 cells at 0, 12, 24, 36, and 48 h after transfection with the TRPV4-EGFP plasmid. As was the case for Ca_V1.2 channels, the sizes of the TRPV4 clusters followed exponential distributions at each time point (Fig. 4, B and C). As we found for Ca_V1.2 channels, the mean area and density of TRPV4 channel clusters increased rapidly over a period of ∼12 h and reached a plateau at ∼24 h (Fig. 4, D and E). Similarly, the TRPV4 cluster size and density data were fit with exponential functions with T_1/2 at 6.4 and 5.7 h after transfection for cluster size and cluster density, respectively. The common finding that the cluster sizes and cluster densities of these two types of channels increase rapidly over a short period following transfection and expression but then reach a steady state suggests the presence of a regulatory feedback mechanism controlling channel cluster size and density.

Turnover rate of Ca_V1.2 and TRPV4 channels in the membrane of tsA-201 cells

By tuning the three parameters in our model through iterative simulations, we found a connection between P_g and P_R to channel cluster size and between P_n channel cluster density.

Thus, properly constraining our model required information about channel turnover rates within cell membranes. To this end, we expressed photoactivatable-GFP tagged Ca_V1.2 or TRPV4 channels (PA-Ca_V1.2 and PA-TRPV4) in tsA-201 cells. Photoactivatable-GFP is nonfluorescent until it is exposed to a brief blue light pulse. Thus, PA-Ca_V1.2 and PA-TRPV4 fluorescence is limited to the set of channels expressed at the time of photoactivation. PA-Ca_V1.2 and PA-TRPV4 fluorescence intensity is therefore proportional to the number of channels expressed and could be used to determine dwell time (i.e., the time these channels spend in the membrane).

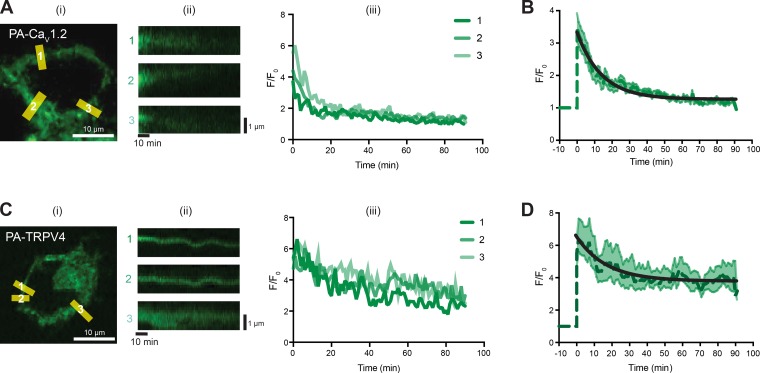
For these experiments, cells expressing PA-Ca_V1.2 or PA-TRPV4 (Fig. 5) were imaged before and after a 10-s exposure to 405-nm light to activate the PA-GFP. In Fig. 5 A, we show a confocal image from a center section of a representative tsA-201 cell expressing PA-Ca_V1.2. As expected, after photoactivation, the fluorescence was largely limited to the surface membrane of the cell. For analysis, we measured the spatially averaged fluorescence and generated pseudo-line scans from multiple regions in the membrane from 2-D image stacks. The time course of fluorescence intensity in three sites in the membrane is shown to the right of the 2-D image in Fig. 5 A. Note that at each site, over a period of 90 min after photoactivation, PA-Ca_V1.2 fluorescence nearly disappears, suggesting that most channels are removed from the membrane within this period. Fig. 5 B shows the averaged, normalized fluorescence intensity from all the membrane sites analyzed from multiple cells. The decaying phase of the curve was fit with a single exponential function with a T_1/2 of 9.74 min.

Figure 5.

Dwell times for Ca_V1.2 and TRPV4 channels in tsA-201 cells are fast. (A) Representative image of a tsA-201 cell transfected with Ca_V1.2-PA-GFP immediately after stimulation (i), with corresponding labeled ROI slices (ii), and fluorescent traces of the ROI slices (iii). F, fluorescence. (B) Mean time course of Ca_V1.2-PA-GFP normalized fluorescence (dark green dashed line) and SEM at each time (light green shaded area) of all normalized ROIs. Time course was fit with an exponential function (black line). 26 ROIs from nine cells were averaged. (C) Representative image of a tsA-201 cell transfected with TRPV4-PA-GFP immediately after stimulation (i), with corresponding labeled ROI slices (ii), and fluorescent traces of the ROI slices (iii). (D) Mean time course of TRVP4-PA-GFP normalized fluorescence (dark green dashed line) and SEM at each time (light green shaded area) of all normalized ROIs. Time course was fit with an exponential function (black line). 17 ROIs from 6 cells were averaged.

In Fig. 5 C, we show the results of equivalent experiments for cells expressing PA-TRPV4. As in the case of PA-Ca_V1.2, PA-TRPV4 fluorescence in the membrane increased following 405-nm illumination and decayed with time. However, unlike PA-Ca_V1.2, PA-TRPV4 fluorescence seems to reach a steady state around 45% of the initial maximum signal. Fig. 5 D shows the averaged (with SEM) normalized fluorescence and decay of all the analyzed sites. These data suggest that while a population of TRPV4 channels is removed from the membrane, a larger subset of channels either remains embedded within the membrane or is removed but then recycled back to it. A T_1/2 of 11.59 min for the first population was estimated by fitting a single exponential function.

Model captures dwell times and time-dependent assembly of Ca_V1.2 and TRPV4 channel clusters

Our goal in acquiring the experimental measurements of the time course of channel cluster formation and channel turnover rate or dwell time described above was to extend our model beyond its successful representation of steady-state conditions (Fig. 2). That is, could our model replicate the time-dependent assembly of Ca_V1.2 and TRPV4 channel clusters that we observed experimentally in tsA-201 cells (Fig. 3 and 4) while incorporating the membrane dwell times that we measured (Fig. 5).

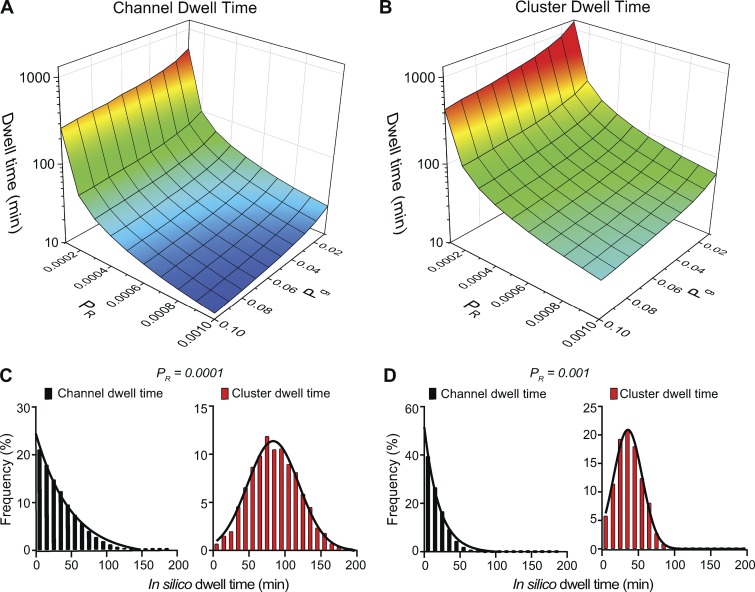
Fig. 6 shows the relationship between channel and cluster dwell times and model parameters P_g and P_R. Channel and cluster dwell times are independent of model parameter P_n, as dwell times correspond to events following nucleation. Note that decreasing P_R or decreasing P_g increases the membrane dwell times for both individual channels (Fig. 6 A) and channel clusters (Fig. 6 B). Further, these data suggest that the dwell times of a channel or a cluster in the membrane is determined by individual P_g values. For example, the predicted dwell time in the membrane of a cluster in a cell with P_g = 0.07 and P_R = 0.0007 (P_g/P_R = 100) is 12 min, while the predicted dwell time in a cell with P_g = 0.1 and P_R = 0.001 (P_g/P_R = 100) is 9 min.

Figure 6.

P_gand P_R determine channel and cluster dwell time. (A and B) Surface plots showing the relationships between P_g, P_R, and channel dwell time (A) or cluster dwell time (B). (C and D) Frequency distributions of channel and cluster dwell times with P_R equal to 0.0001 (C) or 0.001 (D). For the simulations in C and D, P_g and P_n were 0.01 and 0.00006, respectively.

We plotted the distributions of membrane dwell times for individual channels and channel clusters with a P_g of 0.01 and P_R of 0.0001 (Fig. 6 C) or 0.001 (Fig. 6 D). Regardless of the magnitude of P_g and P_R, our model generated exponential membrane dwell time distributions for individual channels that were exponential and Gaussian dwell time distributions for channel clusters. The mean dwell times in the membrane obtained from our model for both individual channels (60 min) and channel clusters (75 min) using a P_R of 0.0001 were similar to those suggested for Ca_V1.2 in neuronal dendrites (≈1 h; Di Biase et al., 2011). In Video 2, we show the effects of varied P_g and P_r values on channel and cluster dwell times in the membrane.

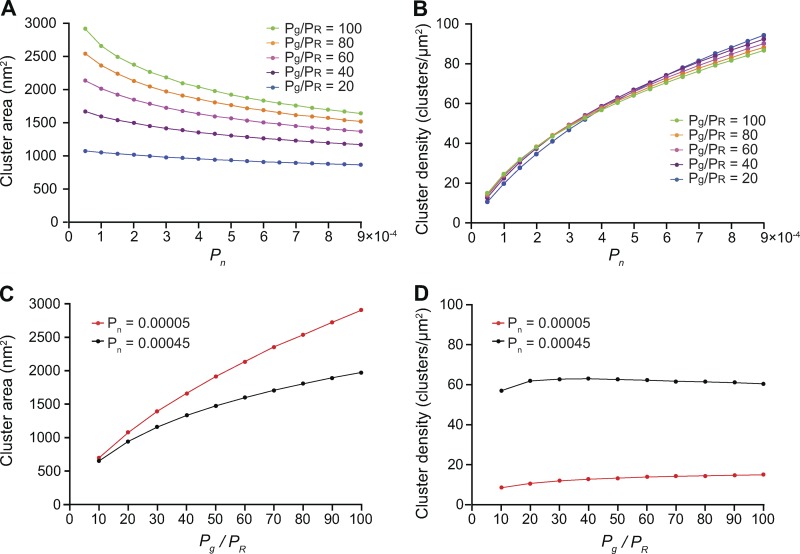
Because the single-channel and channel cluster membrane dwell times are predominantly set by the value of P_g in our model, we examined the effects of the parameters P_R and P_n on cluster area and densities after setting P_g to 0.07, the value that reproduced our experimental measurements of the area of Ca_V1.2 and TRPV4 channel clusters (Figs. 3 and 4). As shown in Fig. 7 A, we found that setting the values of P_g and P_R in ratios ranging from 20 to 100 resulted in increasing channel cluster areas and that a P_g/P_R ratio >50 was required to generate clusters with areas similar to those measured in our experiments for Ca_V1.2 and TRPV4 in tsA-201 cells 48 h after transfection. This is important, as it indicates that channel cluster sizes are determined by the P_g/P_R ratio and not by individual P_g and P_R values.

Figure 7.

In silico stochastic self-assembly of protein clusters with realistic sizes and densities. (A) Plot of the relationships between P_n and cluster area at P_g/P_R ratios equal to 20 (P_g = 0.07, P_R = 0.0035), 40 (P_g = 0.07, P_R = 0.00175), 60 (P_g = 0.07, P_R = 0.001166667), 80 (P_g = 0.07, P_R = 0.000875), and 100 (P_g = 0.07, P_R = 0.0007). (B) Relationships between P_n and cluster density at P_g/P_R ratios equal to 20 (P_g = 0.07, P_R = 0.0035), 40 (P_g = 0.07, P_R = 0.00175), 60 (P_g = 0.07, P_R = 0.001166667), 80 (P_g = 0.07, P_R = 0.000875), and 100 (P_g = 0.07, P_R = 0.0007). For simulations in A and B, we averaged cluster area and density values at steady state for 2,000 iterations. (C) Effect of P_g/P_R ratios on cluster area. (D) Effect of P_g/P_R ratios on cluster density. (C and D) For these simulations, we set the value of P_n = 0.00005 (red traces) and P_n = 0.00045 (black traces), P_g = 0.07 and P_R ranged between 0.007 and 0.0007 to achieve P_g/P_R ratios of 10–100.

We also found that the influence of P_g/P_R ratios on channel cluster formation in our model is affected by P_n. For example, cluster area decreases as P_n is increased. This can be explained by the fact that when the P_n value is small, the probability of channel insertion decreases, and the channel clusters grow according to the specific values of P_g and P_R. However, when P_n is increased, the probability of channel insertion increases, resulting in the initiation of multiple clusters with large variations in size and a decrease in mean cluster area, as shown in Fig. 7 A. In contrast, cluster density is independent of the P_g/P_R ratio and mainly determined by P_n (Fig. 7 B).

To further illustrate the effects of P_R and P_n on channel cluster area, we show the results of a series of simulations using two different P_n values (Fig. 7 C): 0.00045 (black trace) and 0.00005 (red trace). Similarly, the effects of P_R and P_n on channel cluster density are shown in Fig. 7 D. These two P_n values were chosen because they generated simulated channel cluster areas similar to those observed in tsA-201 cells expressing Ca_V1.2-EGFP (Fig. 3) or TRPV4-EGFP (Fig. 4; i.e., P_n = 0.00045) or to those reported in studies in the endogenous channels native cells (i.e., P_n = 0.00005; Mercado et al., 2014; Dixon et al., 2015; Tajada et al., 2017).

In silico stochastic self assembly of Ca_V1.2 and TRPV4 clusters

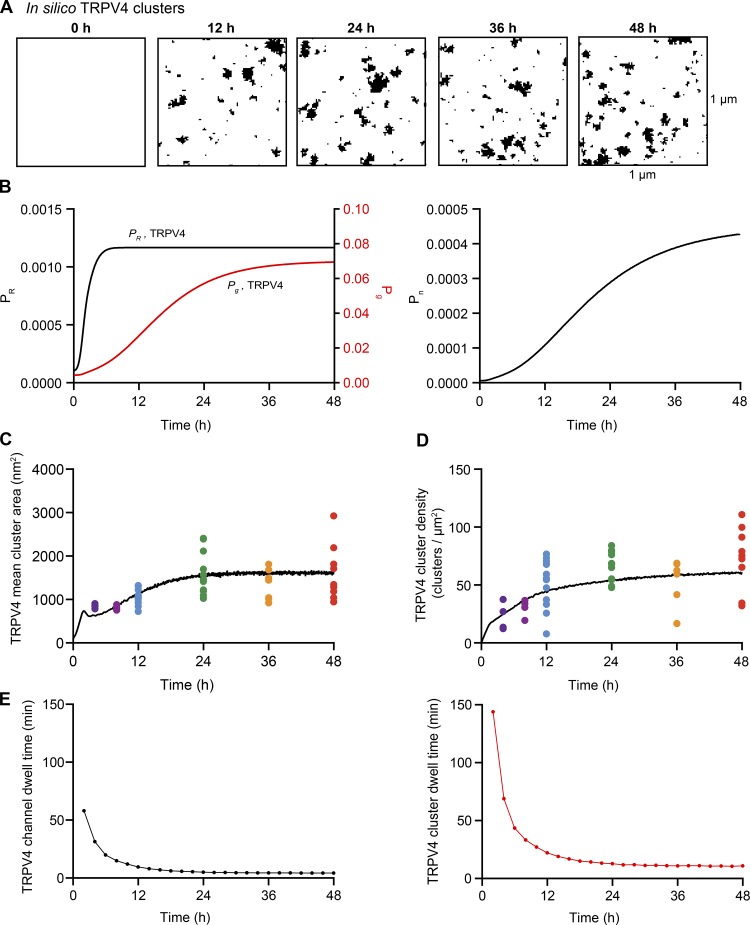
As our model successfully simulated the creation of channel clusters with size, densities, and dwell times similar to those observed experimentally, we set out to use this model to replicate the experimental data we acquired on the time courses of Ca_V1.2 and TRPV4 channel cluster formations expressed in tsA-201 cells (Figs. 3 and 4). To do so, images were generated on every iteration of the model using the time-dependent probability functions P_g, P_n, and P_R. In Figs. 8 A and 9 A, we defined the time-dependent probability functions of P_g, P_n, and P_R to be sigmoid functions. The rationale for this was our own data showing that the time course of Ca_V1.2 and TRPV4 cluster growth (P_g) and densities (P_n) followed a sigmoidal distribution and the work by Green et al. (2007) suggesting that Ca_V1.2 channel internalization in neurons (i.e., P_R) increased as Ca_V1.2 channel number increased. The range of P_n values used were determined by the density data in Figs. 3 and 4 as well as the P_n-density relationships in Fig. 7.

Figure 8.

Sigmoidal time-dependent changes in P_g, P_n, and P_R reproduce the time course of Ca_V1.2 cluster formation in the plasma membrane of tsA-201 cells. (A) Plots of P_g,Cav1.2 (purple), P_n,Cav1.2 (orange), and P_R,Cav1.2 (green) versus time. $P_{R,Cav1.2}=\left[1/\left(1+5e^{-60t}\right)\right]*0.001166667$, $P_{g,Cav1.2}=\left[1/\left(1+15e^{-12t}\right)\right]*0.07$, and $P_{n,Cav1.2}= \left[1/\left(1+2000e^{-27t}\right)\right]*0.00045$. (B) In silico images of Ca_V1.2 clusters at 0, 12, 24, 36, and 48 h after the initiation of expression using the parameters in A. (C and D) The black trace depicts the time course of mean cluster area (C) and densities of simulated clusters (D). Colored dots represent the superimposed experimental data from Fig. 3. (E) Mean Ca_V1.2 channel (black) and cluster (red) dwell times based on the sigmoidal functions P_g, P_n, and P_R.

Figure 9.

Sigmoidal time-dependent changes in P_g, P_n, and P_R reproduce the time course of TRPV4 cluster formation in the plasma membrane of tsA-201 cells. (A) Plots of P_g,TRPV4 (purple), P_n,TRPV4 (orange), and P_R,TRPV4 (green) versus time. $P_{R,TRPV4}= \left[1/\left(1+10e^{-60t}\right)\right]*0.001166667$, $P_{g,TRPV4}= \left[1/\left(1+15e^{-12t}\right)\right]*0.07$, and $P_{n,TRPV4}=\left[1/\left(1+75e^{-16t}\right)\right]*0.00045$. (B) In silico images of TRPV4 clusters at 0, 12, 24, 36, and 48 h after the initiation of expression using the parameters in A. (C and D) The black trace depicts the time course of mean cluster area (C) and densities of simulated clusters (D). Colored dots represent the superimposed experimental data from Fig. 4. (E) Mean TRPV4 channel (black) and cluster (red) dwell times based on the sigmoidal functions P_g, P_n, and P_R.

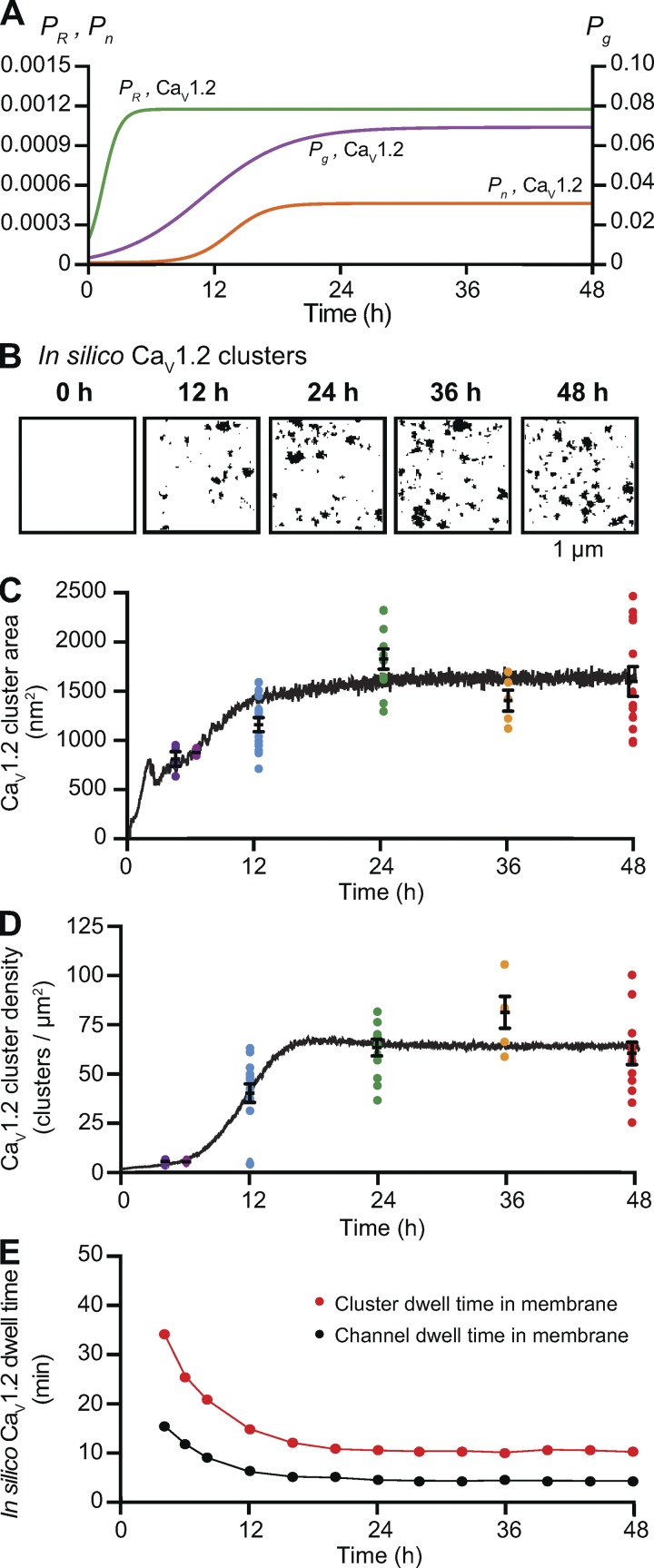
In the case of Ca_V1.2 channels, the time-dependent probability functions P_g,Cav1.2 and P_n,Cav1.2 reached steady state in ∼18 h. Similarly, in the case of TRPV4 channels, P_g,TRPV4 and P_n,TRPV4 reached steady state in ∼20 h. P_R,Cav1.2 and P_R,TRPV4 however, reached their steady states in ∼8 h, which is critical as the ratio between P_R and P_g controls the cluster area. Figs. 8 B and 9 B show computer-generated 2-D images of Ca_V1.2 and TRPV4 channel clusters at various iterations corresponding to 0, 12, 24, 36, and 48 h after transfection.

In Figs. 8 (C and D) and 9 (C and D), we plotted the results obtained from the model simulations (black trace) relative to our experimental data points for the sizes and densities of channel clusters. Cluster sizes for Ca_V1.2 and TRPV4 channels are similar, but there is a key difference in their densities. The cluster density for Ca_V1.2 channels is low relative to TRPV4 at 4 and 8 h. This behavior is reproduced by the time-dependent probability function for P_n.

We could extract the membrane dwell times for individual channels and channel clusters of Ca_V1.2 (Fig. 8 E) and TRPV4 channels (Fig. 9 E) from these simulations. The dwell times in the membrane of individual Ca_V1.2 and TRPV4 channels (≈15 min) and channel clusters (≈35 min) were initially high but decreased to lower steady-state levels after ∼12 h. At 48 h, the predicted dwell times of both individual channels (Ca_V1.2 and TRPV4, 4.2 min) and channel clusters (Ca_V1.2 and TRPV4, 10.3 min) were quite similar for the two channel types. These data suggest that steady-state channel organization for either channel type can be attained by time-dependent changes in P_g and P_n and a relatively rapid turnover rate for both individual channels and clusters. Further, the data suggest feasible set points for P_g and P_n in living cells.

Feedback control of the stochastic self-assembly of Ca_V1.2 and TRPV4 clusters

As mentioned earlier, Green et al. (2007) suggested that Ca_V1.2 channel internalization increases as the number of channels increases, indicating some level of feedback between channel number and P_R, presumably as mediated through intracellular Ca²⁺ levels. Thus, we augmented our model to demonstrate how Ca_V1.2 and TRPV4 channel cluster size and density might be regulated by a feedback mechanism dependent on the number of channels present on the grid. To do so, we set the rates of cluster growth proportional to the number of channels present, represented by the first term (r_xN; x = n, g, or R) in Eqs. 1, 2, and 3 in Materials and methods. This term provides the positive feedback component of the model. The second term (P_x/K_x; x = n, g, or R) in Eqs. 1, 2, and 3 is responsible for the negative feedback component of the model. When the number of channels is small, the positive feedback process dominates. As the number of channels becomes larger, the negative feedback process dominates.

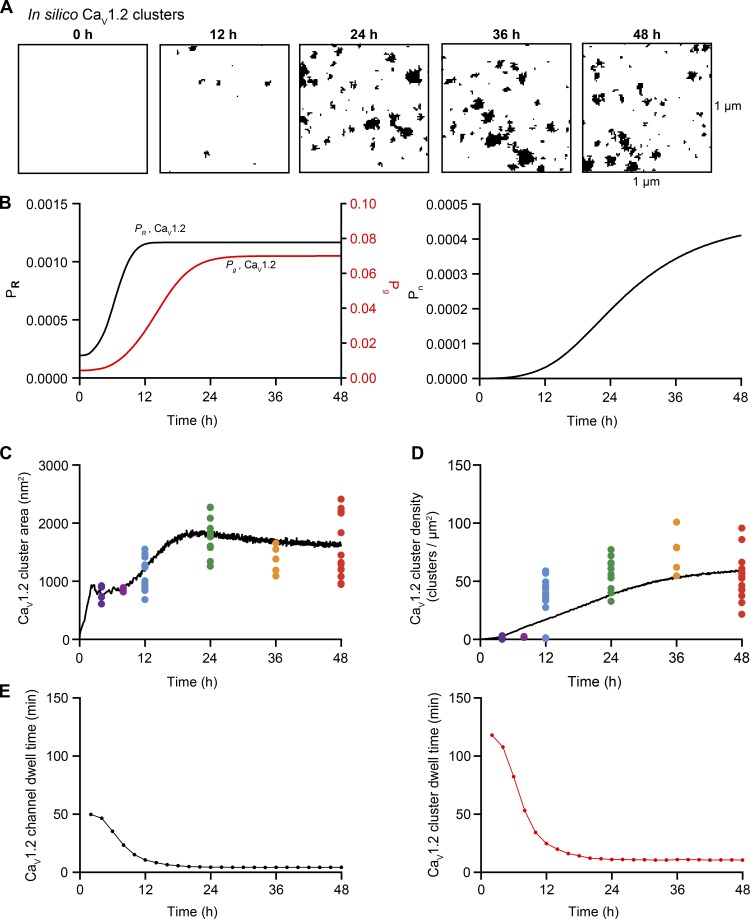
The impact of these additional terms in the model is shown in Fig. 10 for Ca_V1.2 and in Fig. 11 for TRPV4 channels. Figs. 10 A and 11 A show simulated images of Ca_V1.2 and TRPV4 channel clusters at 0, 12, 24, 36, and 48 h after transfection. The positive and negative feedback processes create sigmoidal curves for P_g, P_R, and P_n (Figs. 10 B and 11 B). The time course of cluster growth is governed by the product of the P_g and P_R curves. Accordingly, depending on the shape of P_g and P_R curves, the cluster sizes may have two phases. Cluster density was mainly determined by a sigmoidal P_n curve.

Figure 10.

Feedback model for Ca_V1.2 cluster formation. (A) In silico images of Ca_V1.2 clusters at 0, 12, 24, 36, and 48 h after the initiation of expression. (B) Solutions to the feedback model equations $\frac{d{P}_R}{dt}$, $\frac{d{P}_g}{dt}$, and $\frac{d{P}_n}{dt}$. (C and D) The black trace depicts the time course of mean cluster area (C) and density (D) of simulated Ca_V1.2 clusters. Colored dots represent the superimposed experimental data from Fig. 3. (E) Predicted mean Ca_V1.2 channel (black) and cluster dwell times (red) based on the feedback model.

Figure 11.

Feedback model for TRPV4 cluster formation. (A) In silico images of TRPV4 clusters at 0, 12, 24, 36, and 48 h after the initiation of expression. (B) Solutions to the feedback model equations $\frac{d{P}_R}{dt}$, $\frac{d{P}_g}{dt}$, and $\frac{d{P}_n}{dt}$. (C and D) The black trace depicts the time course of mean cluster area (C) and density of simulated TRPV4 clusters (D). Colored dots represent the superimposed experimental data from Fig. 4. (E) Predicted mean TRPV4 channel (black) and cluster dwell times (red) based on the feedback model.

In Figs. 10 (C and D) and 11 (C and D), we plotted the simulated and experimentally measured and cluster sizes and densities for Ca_V1.2 and TRPV4 channels. The simulations show that increasing P_n,Cav1.2 (from 2e-07 to 0.00045), P_g,Cav1.2 (from 0.004 to 0.07), and P_R,Cav1.2 (from 0.0002 to 0.0012; Fig. 10 B) or P_n,TRPV4 (from 0.000006 to 0.00045), P_g,TRPV4 (from 0.004 to 0.07), and P_R,TRPV4 (from 0.0001 to 0.0012; Fig. 11 B) increases channel cluster areas and densities over time to levels similar to those observed experimentally. In the case of Ca_V1.2, P_g,Cav1.2, P_R,Cav1.2 and P_n,Cav1.2 reached plateau levels at ∼24, 10, and 16 h after transfection, respectively. In the case of TRPV4, P_g,TRPV4, P_R,TRPV4, and P_n,TRPV4 values plateaued ∼24, 6, and 24 h, respectively.

We also extracted the membrane dwell times of individual Ca_V1.2 (Fig. 10 E) and TRPV4 channels (Fig. 11 E) and clusters from simulations using the feedback model. With the parameters used in our simulations, the mean channel (Ca_V1.2 = 50 min; TRPV4 = 60 min) and channel cluster (Ca_V1.2 = 120 min; TRPV4 = 140 min) membrane dwell times were initially high. However, these values quickly (i.e., after ∼4 h) decreased and then remained relatively stable over time for both channels types, such that at 48 h, the predicted channel and cluster dwell times for Ca_V1.2 were 4.3 and 10.5 min, respectively, and for TRPV4 were 4.3 and 10.9 min, respectively. To demonstrate how our feedback model works, we created videos of simulations of Ca_V1.2 and TRPV4 trafficking and cluster formation in the membrane using the P_g, P_R, and P_n values in Figs. 10 and 11 (Video 3 and Video 4).

The two methods we used to reproduce our experimental measurements of cluster formation for Ca_V1.2 (Fig. 3) and TRPV4 (Fig. 4) channels data are complementary and supportive of the concept that channel cluster size and density are regulated via feedback mechanisms. In the first method, we used empirically derived assumptions regarding time-dependent changes in P_R, P_n, and P_g. This first model predicts that in order to reach a plateau phase in cluster size and density, we must increase the parameters P_n, P_g, and P_R until reaching a constant or equilibrium level. We proposed that the curves should be sigmoidally shaped such that changes in cluster size and density would be constrained to the desired values of P_n, P_g, and P_R we observed in tsA cells. In the second method, the behavior of P_n, P_g, and P_R through time was modeled using differential equations coupled by the total number of channels, allowing us to explicitly include a feedback mechanism.

Discussion

Using a combination of experimental and computer modeling approaches, we have made five important observations regarding the formation of ion channel clusters and trafficking in living cells. First, the distributions of clusters of the five types of channels studied (Ca_V1.2, BK, TRPV4, Ca_V1.3_s, and Ca_V1.3_L) were all described by a single exponential function regardless of the type of cell they are expressed in, supporting the hypothesis that the presence of ion channels clusters in cell membranes is consequent to a stochastic, self-assembly process. Second, Ca_V1.2 and TRPV4 channel clusters form in tsA-201 cells with an initial period of rapid growth in size, after which they are maintained in a steady state. Third, this steady-state form in tsA-201 cells is maintained by a relatively fast turnover rate of Ca_V1.2 and TRPV4 channels. Fourth, our model predicts that steady-state size distributions of membrane channel clusters could be sustained by a range channel turnover rates. While we are aware of the possibility that our measurements are based solely on a heterologous expression system and might differ from those made in other cell types, our fifth observation is that both our experimentally measured and predicted membrane dwell times are similar to those reported for Ca_V1.2 in cultured cardiac HL-1 cells (Conrad et al., 2018) and primary neurons (Di Biase et al., 2011), as well as to mean transcript and protein dwell times (Schwanhäusser et al., 2011).

To illustrate how our model could be used by physiologists interested in investigating the role of a particular interacting protein in ion channel clustering, we have considered three potential scenarios in which a change in a physiological process alters ion channel cluster area or density via changes in one of the three model parameters (i.e., P_n, P_g, or P_R). In the first scenario, let us propose that the insertion of channels at the plasma membrane is enhanced by the up-regulation or activation of a signaling pathway. In our model, this process would result in an increase in the parameter P_n. An example of this could be the Ca²⁺-dependent up-regulation of K⁺ channels expression via the activation of the calcineurin/nuclear factor of activated T cells signaling pathway. As first demonstrated by Amberg et al. (2004) and (Rossow et al., 2004, 2006, 2009), Kv4 and Kv2 channel expression is tightly regulated by intracellular Ca²⁺ in cardiac and vascular cells. BK channel expression is also regulated by Ca²⁺ levels in smooth muscle (Nieves-Cintrón et al., 2007, 2008). In this scenario, the increase in the expression of the channels will increase the available pool of channels that can be inserted at the plasma membrane, increasing cluster density. Interestingly, the differences in Ca_V1.2 and TRPV4 cluster densities reported here among tsA-201 cells, smooth muscle, and ventricular myocytes were simulated by variations in the P_n among these cells. These data suggest that the level of expression of these channels and/or the proteins related with the trafficking and delivery of these channels to the plasma membrane varies between cells.

In the second scenario, we consider the possibility that the insertion of new channels is favored to occur in the same sites where other channels have been previously inserted because of the up-regulation of an interacting protein. In our model, this process would increase P_g. An example of such a protein is BIN1, which binds to the inner face of the plasma membrane and forms lattices via the cooperative binding of other molecules, thus creating membrane microfolds (Adam et al., 2015). In ventricular myocytes, BIN1 has been implicated in the formation of membrane curvatures (Lee et al., 2002) and in anchoring microtubules where newly synthesized Ca_V1.2 channels are delivered to the surface membrane (Hong et al., 2010, 2014). As such, BIN1 could function to increase the local concentration of Ca_V1.2 channels at specific sites in the plasma membrane, enhancing their clustering. Consistent with this, De La Mata et al. (2019) found that overexpression BIN1 in human embryonic stem cell–derived cardiomyocytes (hESC-CMs) increased Ca_V1.2 cluster size. Thus, BIN1 could be acting to direct the insertion of Ca_V1.2 channels in the sarcolemma of cardiac myocytes, which would increase the P_g of these channels. Importantly, in the case of channels that undergo functional coupling (i.e., L-type Ca²⁺ channels), the increase in cluster size could strengthen the coupling between these channels, resulting in a further increase in the amplitude of ion flux.

Finally, in the third scenario, we imagine a situation in which the removal of individual ion channels or ion channel clusters from the plasma membrane is enhanced by an interacting protein. In our model, this process would result in an increase in the parameter P_R. An example of this could be the activation of the HECT ubiquitin ligase ALP4, which has been linked to TRPV4 channel internalization (Wegierski et al., 2006). Another example is the tumor suppressor eukaryotic initiation factor 3 subunit e/Int6, which induces internalization of Ca_V1.2 channels in neurons (Green et al., 2007). In this scenario, the activation of these proteins will likely be associated with an overall decrease in channel membrane dwell time and a decrease in cluster size.

An important observation we made in the course of this study is that whereas the sizes and densities of Ca_V1.2 and TRPV4 channel clusters expressed in tsA-201 cells increased rapidly after transfection, both parameters reached a plateau within 24 h. These results suggest that plasma membrane expression levels and clustering of exogenously expressed Ca_V1.2 and TRPV4 channels is under the control of a feedback mechanism. Indeed, recent live-cell imaging experiments indicate that Ca_V1.2 containing vesicles in tsA-201 cells could have multiple mechanisms for interacting and delivering channel to the plasma membrane (Ghosh et al., 2018). Similar proposals have been put forth for endogenous Ca_V1.2 in cardiac myocytes (Rosati et al., 2011) and neurons (Green et al., 2007). The latter report suggested that action potential firing rate, channel activity, and a Ca²⁺-driven increase in Ca_V1.2 internalization (i.e., P_R) were responsible for regulating plasma membrane expression levels of Ca_V1.2. Our feedback model relies exclusively on channel number and does not take into account the state of the channel (e.g., open, deactivated, inactivated, or desensitized). Thus, a desensitized or inactivated channel would have the same probability of being removed by internalization or endocytosis than a deactivated or open channel. Mechanisms determining steady-state levels of these ion channels in cardiac and smooth muscle will need further study.

Another intriguing question posed by our work is whether the membrane dwell times and time course of clustering of Ca_V1.2 and TRPV4 channels in native cells are similar to those we found operating in tsA-201 cells. The work by De La Mata et al. (2019) suggests that in hESC-CMs, Ca_V1.2 cluster sizes and densities increased from the induction of differentiation until day 30. Interestingly, the channel cluster sizes and densities achieved at this time point were similar to those in adult ventricular myocytes, raising the possibility that they had reached an intrinsically defined level of steady-state expression and clustering. Regardless of whether a steady state had been reached or not, these hESC-CM data suggest that the rates of cluster nucleation, growth, removal, and thus channel membrane dwell times are likely different among cells at different levels of differentiation. A testable hypothesis is that the membrane dwell time of channels is higher in rapidly dividing cells like tsA-201 cells than in fully differentiated, nondividing cells like ventricular myocytes and that upon stimulation (e.g., autonomic nervous system or physiological and pathological hypertrophy), changes in gene expression, channel delivery, recycling, and/or protein degradation could increase channel dynamics.

Another key question raised by our study is whether membrane channels are internalized individually or through the removal of entire clusters. Our experimental data and model simulations do not provide a definitive answer, but simulations in which channels were exclusively removed one at a time predicted the formation of a large number of macroclusters with parameters similar to those used to reproduce experimental data from cardiac myocytes, smooth muscle cells, neurons, and tsA-201 cells. However, macroclusters predicted by the model were not observed experimentally. Accordingly, we modified the model so that channel internalization would be stochastic and involve individual channels as well as channel clusters of varied sizes. Considering that the area of an endocytic vesicle could range from 1,200 to 1.26 × 10⁵ nm² and the mean cluster areas reported here range from ∼1,900 to 3,700 nm², this assumption seems reasonable. Future experiments will be required to test this hypothesis.

Finally, while our data reveal that in smooth muscle and tsA-201 cells, channels are clustered randomly throughout the entire cell surface, it is important to mention that variations in channel expression both between and within cells are commonly observed and reported. To cite just a few examples, Na_V1 channels are highly concentrated in the nodes of Ranvier of myelinated axons but largely absent from the internodal membrane (Hille, 2001), Ca_V1.2 channels are preferentially expressed in along the T-tubules of ventricular myocytes (Dixon et al., 2015), the Na⁺/H⁺ exchanger is absent from the T-tubules (Garciarena et al., 2013), and the Na⁺/K⁺α2ATPase proteins are distributed preferentially in the T-tubules and surface sarcolemma (Yuen et al., 2017). While these regional variations in channel expression may seem incompatible with our model, they could still be the result of a stochastic, self-assembly process operating within a restricted cellular domain. For example, our data suggest that Ca_V1.2 channel clusters are stochastically self-assembled along the T-tubules of ventricular myocytes, but not throughout the entire cell. These seemingly contradictory observations can be reconciled by proposing that there may be variations in P_n, P_g, or P_R in different compartments of the same cell that lead to stochastic self assembly of clusters therein. The possibility of regional variations in P_n, P_g, and P_r should be addressed in further studies.

In summary, we have provided a set of experimental measurements and computer simulations that support the hypothesis that the formation of ion channel clusters in the surface membrane of excitable cells reflects the operation of a stochastic self-assembly process without the involvement of any active mechanism of aggregation, such as agrin-induced recruitment of acetylcholine receptors into the postsynaptic motor endplate (Sanes and Lichtman, 2001), ankyrin G–mediated clustering of voltage-gated Na⁺ channels and Kv7 channels at nodes of Ranvier (Nelson and Jenkins, 2017), and Kv2 channel clustering by VAPA and VAPB proteins (Johnson et al., 2018; Kirmiz et al., 2018). Indeed, our data are consistent with the view that membrane channel clustering is the default organization for multiple types of channels in the surface membranes of four different cell types. Notably, our model incorporates a self-regulating mechanism that assumes a feedback process between channel number and channel cluster formation. Our model may be broadly applicable to the distributions of many different types of membrane (bound proteins and channels) in health and disease states. We certainly cannot rule out the possibility that one or more proteins will be found that are not randomly distributed along the surface membrane. Whether or not there is a functional consequence of clustering for all the types of ion channels, as we have found for Ca_V1.2, Ca_V1.3, BK, and TRPV4 channels, remains an open question, but a very important one.