Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2019 Sep 3;10:3961. doi: 10.1038/s41467-019-11822-5

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2019

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

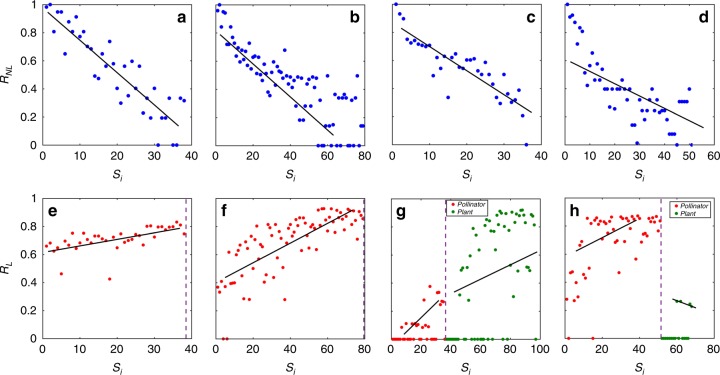
Fig. 2 — Contrasting behaviors of nodal importance ranking in nonlinear and linear control. The four empirical networks are labeled as A, B, C, and D with details given in the “Methods” section. a–d Nonlinear and e–h linear control importance ranking for networks A−D, respectively. For tipping point control of the nonlinear network in a–d, only the pollinator species are subject to external intervention through the managed maintenance of the abundance of a single species. The nodal index on the abscissa of each panel is arranged according to the degree ranking of the node: from high to low degree values (left to right). For the set of nodes with the same degree, their ranking is randomized. (The dependence of nonlinear and linear control importance on the actual degree value is presented in Supplementary Note 2.) The nonlinear control importance is calculated from Eq. (1) for the parameter setting h = 0.2, t = 0.5, $β_{i i}^{(A)} = β_{i i}^{(P)} = 1$ , $β_{i j}^{(A)} = β_{i j}^{(P)} = 0, α_{i}^{(A)} = α_{i}^{(P)} = - 0.3$ , and μ_A = μ_P = 0.0001. The coupled nonlinear differential equations are solved using the standard Runge–Kutta method with the time step 0.01. The distinct feature associated with nonlinear control is that, in spite of the fluctuations, larger degree nodes tend to be more important (i.e., more effective in recovering the species abundances after a tipping point). The linear control importance ranking in e–h can be calculated for all species based on definition (7), because the corresponding artificial linear dynamical network does not distinguish between pollinator and plant species. In each panel, the pollinators (red dots) and plants (green dots) are placed on the left and right side, respectively, and are arranged in descending values of their degree, with a vertical dashed line separating the two types of species. The striking result is that, for the pollinators, their ranking of linear control importance exhibits a trend opposite to that of nonlinear control importance. A similar behavior occurs for ranking based on betweenness centrality and actual degrees (Supplementary Note 2 and Supplementary Figs. 3–5)