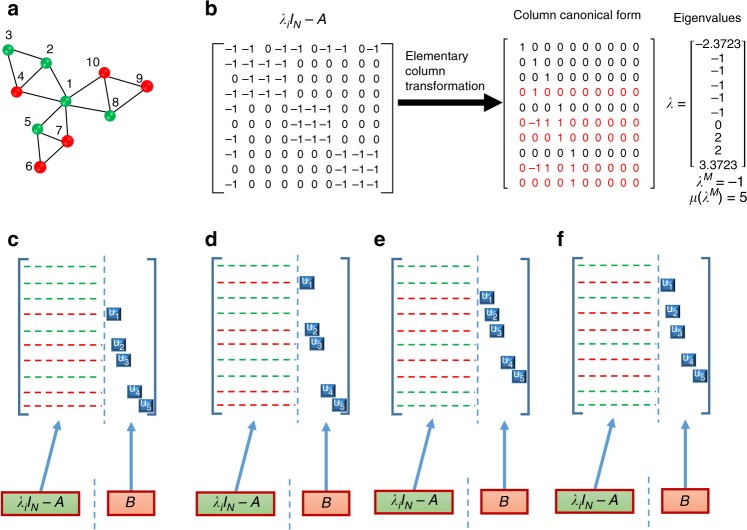
Fig. 6.
Illustration of non-uniqueness of driver node set in linear network control. a A 10-node undirected network. Five eigenvalues of the network connection matrix are identical: λ = −1, so its algebraic multiplicity is five. The geometric multiplicity of this eigenvalue is the number of linearly dependent rows in the matrix , which can be determined through elementary column transforms. b The matrix and its representation after a series of elementary column transforms. The first, second, third, fifth, and eighth rows are distinct from all other rows, so they are linearly independent. The fourth, sixth, seventh, ninth, and tenth rows are linearly dependent rows. Because there are five linearly independent and five linearly dependent rows, the number of ways to choose the latter is 54. c–f Four distinct ways to choose the control input matrix to make the rank of the matrix ten. For this small network of size ten, any one of the nine out of the the ten nodes can be chosen to be a driver node