Skip to main content
. 2005 Mar 2;25(9):2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005

Figure 1.

Figure 1.

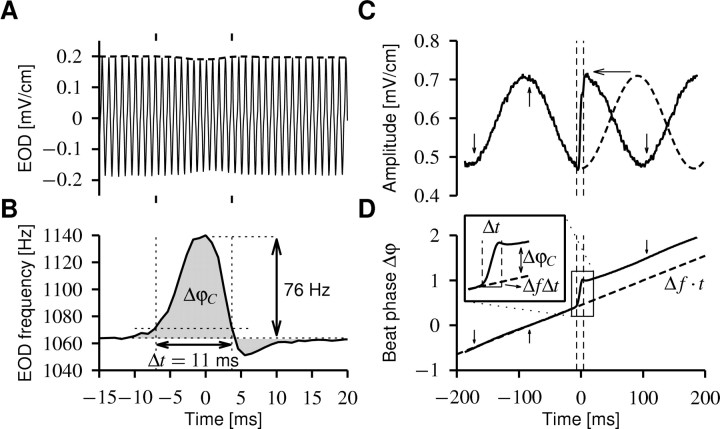
Chirps. A, Looking at the EOD waveform (solid line), a small chirp (within the tic marks) is only visible as a small decrease in EOD amplitude (dashed line). This trace was recorded from the head-tail electrodes that do not pick up an additional stimulus field. B, Plotting the frequency of the EOD reveals the chirp, a transient (Δt = 11 ms) increase in EOD frequency (76 Hz) followed sometimes by a much smaller decrease in EOD frequency. This frequency excursion results in a phase shift ΔφC relative to an EOD without a chirp, which is given by the integral over the EOD frequency minus its baseline frequency (gray area). ΔφC is always positive, because a chirp always increases the EOD frequency. C, The presence of an EOD of a second fish creates a beat; here, with frequency Δf = 5 Hz. The chirp (with in the vertical dashed lines) has a huge impact on the beat pattern (envelope of the EOD, solid line). One-half of a cycle of the beat (dashed line) is compressed (horizontal arrow) within the chirp, thus resulting in a phase shift of the beat. The same chirp as in A is shown but recorded from the transdermal electrodes while applying an artificial EOD on the stimulus electrodes mimicking a second fish. D, The phase Δφ of the beat determines the position of peaks (upward arrow) and troughs (downward arrows) of the beat. Δφ is the difference between the phases of the two EODs. In the absence of chirps, the phases of the EODs φ1 = f1t and φ2 = f2t are determined by their respective frequencies, f1 and f2, and thus the phase of the beat is linearly increasing in time (dashed line; Δφ = φ2 - φ1 =Δft), as determined by the beat frequency Δf = f2 - f1. A chirp leads to a sudden increase in the phase of the beat (solid line), because the phase shift ΔφC of the chirp is added to the phase shift of the beat ΔfΔt and thus accelerates the beat pattern for the duration Δt of the chirp. This is demonstrated by the inset that shows enlarged the time course of the beat phase during the chirp. Note also that the phase increase during the chirp is in good approximation linear.