Abstract
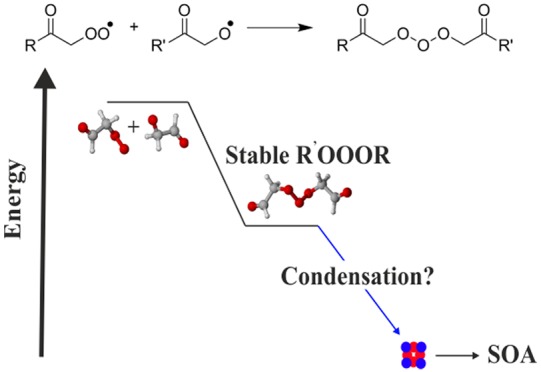
Peroxy (RO2) and alkoxy (RO) radicals are prototypical intermediates in any hydrocarbon oxidation. In this work, we use computational methods to (1) study the mechanism and kinetics of the RO2 + OH reaction for previously unexplored “R” structures (R = CH(O)CH2 and R = CH3C(O)) and (2) investigate a hitherto unaccounted channel of molecular growth, R′O2 + RO. On the singlet surface, these reactions rapidly form ROOOH and R′OOOR adducts, respectively. The former decomposes to RO + HO2 and R(O)OH + O2 products, while the main decomposition channel for the latter is back to the reactant radicals. Decomposition rates of R′OOOR adducts varied between 103 and 0.015 s–1 at 298 K and 1 atm. The most long-lived R′OOOR adducts likely account for some fraction of the elemental compositions detected in the atmosphere that are commonly assigned to stable covalently bound dimers.
Organic peroxy radicals (RO2) produced from the oxidation of volatile organic compounds (VOCs) are known to play an important role in, for example, trace gas removal, generation of ozone, and the formation of secondary organic aerosol (SOA) in the atmosphere.1−4 An important sink pathway of RO2 in polluted environments is the reaction with NO, which leads to the formation of NO2. NO2 subsequently photolyzes in the atmosphere and leads to the net formation of one ozone (O3) molecule. In unpolluted areas, RO2 is mainly lost to reactions with the hydroperoxy radical (HO2) and with other peroxy radicals. Unimolecular H-shift isomerization reactions can outcompete these bimolecular reactions for certain RO2.5,6 Alkoxy radicals (RO) are products of RO2 + RO2 and RO2 + NO reactions. An additional RO source is the photolysis of peroxides.7 Sink pathways of alkoxy radicals in the atmosphere include reaction with O2, leading to the formation of a carbonyl compound and HO2, isomerization via intramolecular hydrogen shifts, and decomposition via bond fission.
Recently, multiple theoretical and experimental studies have reported that the RO2 + OH (hydroxy radical) reaction could be a significant sink channel for peroxy radicals under remote conditions, such as in the marine boundary layer.8−16 This reaction for methyl peroxy radical is reportedly quick, with a rate coefficient of 1.6 × 10–10 cm3 s–1 at 295 K.11 The fast reaction rate partially compensates for the relatively lower concentrations of OH compared to the HO2 radical, and the RO2 + OH reaction may thus compete with the RO2 + HO2 reaction whenever the HO2/OH ratio is low. Studies on larger C2 to C4 alkyl peroxy radicals found the RO2 + OH reaction rate coefficient to be 1.3–1.5 × 10–10 cm3 s–1.17
Studies on CH3O2 + OH13,14 and C2H5O2 + OH15 show that these reactions proceed almost exclusively via the barrierless formation of a ROOOH trioxide intermediate on the singlet surface, with RO + HO2 being the lowest-energy fragmentation channel. This is in agreement with the observed 80% HO2 yield for the CH3O2 + OH reaction.18 For peroxy radicals CH3OO, CH3CH2OO, CH3CH2CH2OO, and CH3CH2CH2CH2OO, the increase in the “R” size corresponded to a decrease in HO2 yield (0.9, 0.75, 0.41, and 0.15, respectively) in the experimental study of the RO2 + OH reaction reported by Assaf et al.19 This points to more efficient stabilization of the larger ROOOH intermediates. Similar mechanistic studies for nonalkyl peroxy radical types have not been carried out. In this work, the kinetics of the RO2 + OH reactions are inspected also for the carbonyl containing acetyl and β-oxo peroxy radicals. Differences in RO2 structures have previously been observed to significantly alter product branching ratios. Hasson et al.,20 for example, reported a strong structure dependence for the different product channels of the RO2 + HO2 reaction, where “R” is either an alkyl, acetonyl, or acetyl group.
Like RO2 and HO2, RO and OH often have similar or analogous reactivities, and one can postulate that the R′O2 + RO reaction should go through a similar trioxide adduct (R′OOOR in this case) as the RO2 + OH reaction. The atmospheric importance of the R′O2 + RO reaction depends on the steady-state RO concentration, which is generally assumed to be small due to the high loss rates of alkoxy radicals. Considering an effective RO loss rate between 1 × 106 and 1 × 103 s–1, together with atmospherically representative values for the RO source terms, we obtain an ambient RO concentration range from 2 to 1 × 105 molecules cm–3 (see section S6 for details). If the formation of the R′OOOR adducts is fast and they are sufficiently stable, they could thus constitute a fraction of the low-volatility organic compounds in the atmosphere referred to as dimers.1,21,22 Recently, R′OOOR formed via a R′O2 + RO reaction was tentatively suggested23 as the mechanism involved in the formation of C19H28O11, a major dimer peak reported in multiple nitrate chemical ionization mass spectrometry-based laboratory and ambient studies of α-pinene ozonolysis.1,24−27
Additionally, the R′O2 + RO reaction along the triplet surface could potentially lead to low barrier product channels, forming, for example, Criegee intermediates (CI; denoted by R–H′•OO• in reaction 2) that play a critical role in the oxidative capacity of the atmosphere and in SOA formation.28−31 The possible reaction channels of R′O2 + RO are
| 1 |
| 2 |
| 3 |
| 4 |
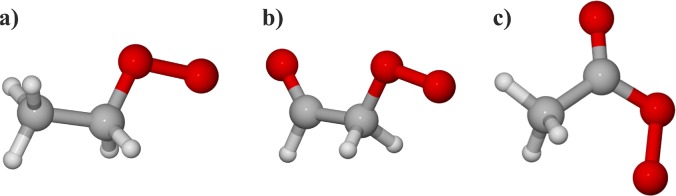
We considered 2-carbon CH3CH2OO, CH(O)CH2OO, and CH3C(O)OO peroxy/alkoxy radicals (see Figure 1 for the RO2 systems; the RO systems were identical except for an oxy radical group instead of a peroxy radical group). For the RO2 + OH reaction, only CH(O)CH2OO and CH3C(O)OO systems were studied here as CH3CH2OO has already been investigated in detail previously.15
Figure 1.
(a) CH3CH2OO, (b) CH(O)CH2OO, and (c) CH3C(O)OO peroxy radicals.
On the singlet surface, the decomposition of the β-oxo CH(O)CH2OOOH adduct primarily follows the CH(O)CH2O + HO2 channel (see section S1 for details), which is analogous to the previously studied alkyl CH3CH2OOOH.15,18,19 However, the acetyl CH3C(O)OOOH adduct will rather decompose into CH3C(O)OH + 1O2 as this channel has a low barrier. Total first-order decomposition rates of CH(O)CH2OOOH and CH3C(O)OOOH adducts were calculated using the master equation solver for multienergy well reactions (MESMER) program and were found to be 2.7 × 10–3 and 1.9 × 103 s–1, respectively. Formation of the adducts is unfavorable on the triplet surface for both sets of reactions (see Figure S5). The reaction stationary points with the energies of the different breakup channels on the singlet and triplet surfaces and the MESMER-simulated pressure and temperature dependencies of the ROOOH formation rate coefficients are provided in section S1.
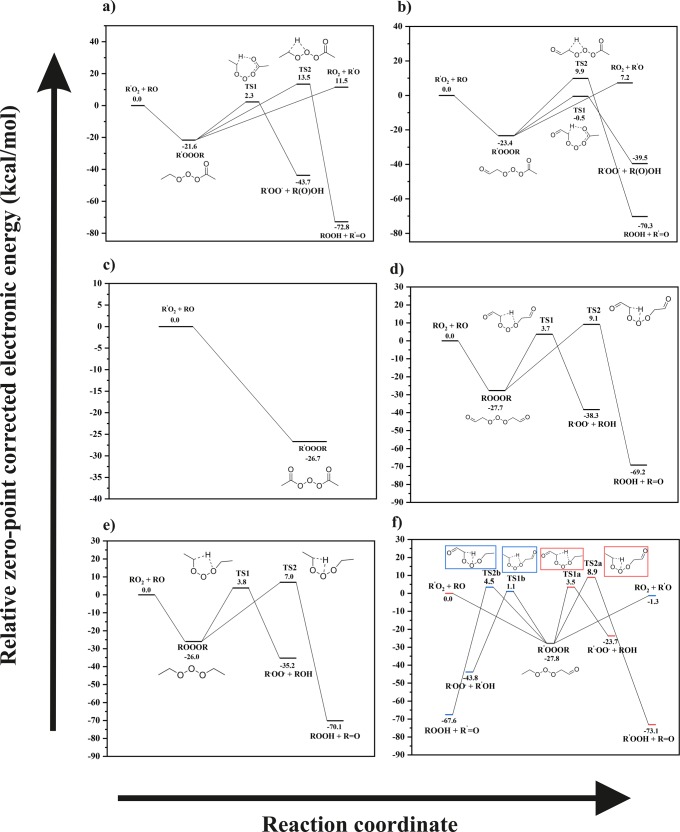
Similarly to the RO2 + OH reaction, R′O2 + RO also forms a trioxide adduct (R′OOOR, in this case) on the singlet surface for the studied systems. A relaxed scan over the R′OO···OR bond showed that this reaction is barrierless, at least at the ωB97X-D/6-31+G(d) level of theory (see section S8 for details). The adduct can then decompose in four ways, illustrated in reactions 1 (back to parent reactants), 2, 3, and 4 (the possible product channels). Figure 2 shows the stationary points of the R′O2 + RO reaction on the singlet surface. The reactants can also form a CI and an alcohol directly. However, this reaction has a barrier of ∼2 kcal/mol and higher in zero-point-corrected energy (∼12 kcal/mol in free energy) for the studied systems and is therefore unlikely to compete with the formation of the R′OOOR adduct. Details of this reaction are provided in section S2. We note that CH(O)CH2OO will undergo a fast 1,4-aldehydic H-shift6 and that the decomposition of the CH3C(O)O acetyloxy radical to form CH3 and CO2 has a very small barrier.7 Especially the CH3C(O)O radical will therefore not live long enough to undergo bimolecular reactions in the atmosphere. The two systems are nevertheless included here for completeness and to demonstrate the effect of reactant structure on the product channels. Other β-oxo peroxy and acetyloxy radicals could have longer lifetimes, and their participation in bimolecular reactions cannot be ruled out.
Figure 2.
Stationary points on the singlet surface of the reaction R′O2 + RO for (a) acetyl (R) + alkyl (R′), (b) acetyl (R) + β-oxo (R′), (c) acetyl (R) + acetyl (R′), (d) β-oxo (R) + β-oxo (R′), (e) alkyl (R) + alkyl (R′), and (f) alkyl (R) + β-oxo (R′) systems calculated at the ROHF-RCCSD(T)-F12a/VDZ-F12//ωB97X-D/aug-cc-pVTZ level.
The R′OOOR adducts are significantly lower in energy relative to the reactants on the singlet surface. Considering the high reactivity of RO radicals and that the reaction was found to be barrierless, the formation of the R′OOOR adduct is likely facile for all atmospherically relevant RO + RO2 combinations. While the decomposition channels of the ROOOH adduct had barriers that were mostly below the reactant energies (and therefore more likely to be competitive; see Figure S1), the transition state energies connecting the two breakup channels of R′OOOR illustrated in reactions 2 and 3 were above the reactant energy for all cases (except for the β-oxo-acetyl case, which had a barrier of −0.5 kcal/mol relative to the reactants for reaction 2; see Figure 2b). The barrier heights for reactions 2 and 3 are ∼23–32 and ∼33–37 kcal/mol above the R′OOOR intermediate, respectively, for all studied systems. These are therefore not competitive with decomposition back into R′O2 + RO (or R′O + RO2). The Criegee-forming channel via the trioxide intermediate (reaction 2) was found to have a relatively low barrier (23–24 kcal/mol relative to the trioxide intermediate) for the acetyl-β-oxo and acetyl-alkyl systems. This is due to the added flexibility afforded by the carbonyl oxygen of the acetyl molecule to the H-shift transition state geometry (see Figure S8). The transition state corresponding to reaction 3 requires contortion of the trioxide group, and the barrier involved is significantly higher.
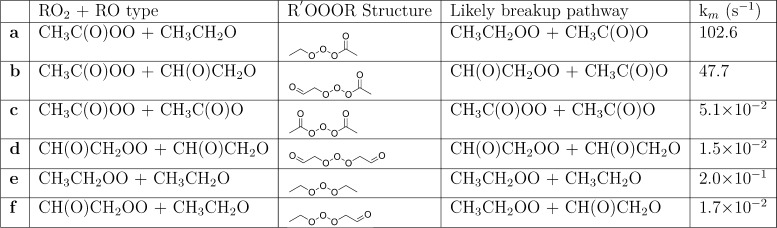
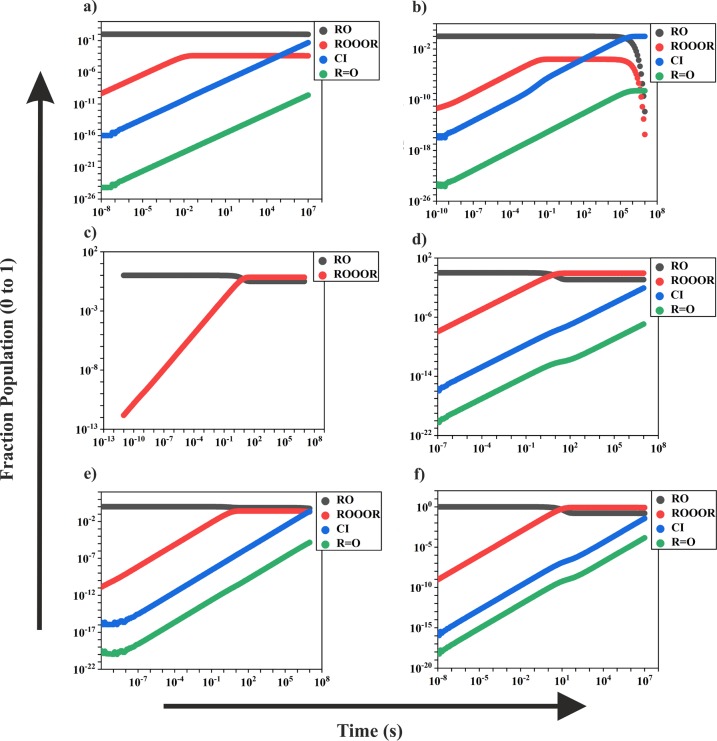
The MESMER-simulated total first-order R′OOOR loss rate coefficients and the likely decomposition channels are shown in Table 1, and species concentration profiles of reactant RO, intermediate R′OOOR, and the possible products CI (R–H′•OO•) and R=O are shown in Figure 3. RO2 was assigned as the excess reactant and given a value of 1 × 109 molecules cm–3 in the simulations as this was calculated to be a roughly representative steady-state peroxy radical concentration in both pristine and polluted conditions (see section S6 for details). Figure 4 shows the first-order R′OOOR decomposition rate coefficients via the different possible channels. The pressure- and temperature-dependent formation rate coefficient of the R′OOOR intermediate for the CH(O)CH2OO + CH(O)CH2O system is shown in Figure 5. Similar plots for the remaining studied systems are provided in section S2. The stationary points on the triplet surface for the studied systems are shown in section S5. Analogous to ROOOH, the formation of R′OOOR adducts was found to be highly unfavorable on the triplet surface.
Table 1. MESMER-Derived Total First-Order Bartis–Widom Phenomenological Loss Rate Coefficients (km) of R′OOOR at 298 K and 1 atm Bath Gas (N2) Pressure.
Figure 3.
MESMER-simulated species profiles of reactant RO, intermediate R′OOOR, and possible products CI (R–H′•OO•) and R=O for (a) acetyl (R) + alkyl (R′), (b) acetyl (R) + β-oxo (R′), (c) acetyl (R) + acetyl (R′), (d) β-oxo (R) + β-oxo (R′), (e) alkyl (R) + alkyl (R′), and (f) alkyl (R) + β-oxo (R′) systems calculated at 298 K, 1 atm bath gas (N2) pressure, and an RO2 concentration of 1 × 109 molecules cm–3.
Figure 4.
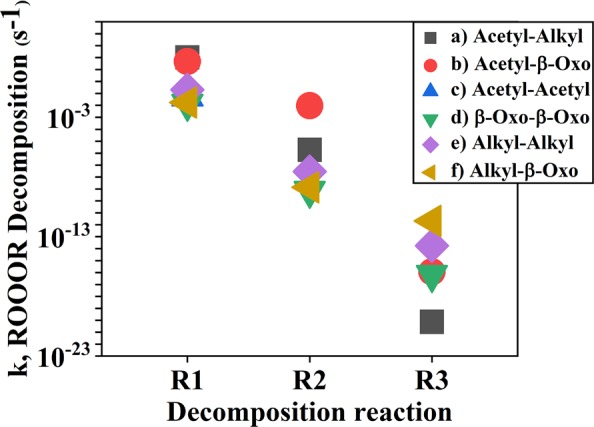
MESMER-simulated R′OOOR decomposition rate coefficients via the different possible product channels for the studied systems calculated at 298 K temperature and 1 atm pressure. R1: R′OOOR → R′O2 + RO; R2: R′OOOR → R–H′•OO• + ROH; R3: R′OOOR → R′OOH + R=O.
Figure 5.
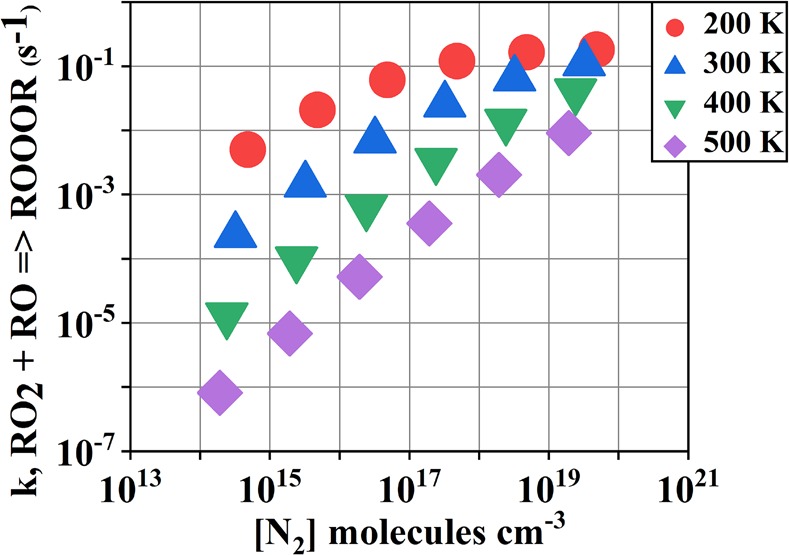
MESMER-simulated temperature and pressure dependence of the R′OOOR formation rate coefficients for the CH(O)CH2OO + CH(O)CH2O system. Pseudounimolecular rate coefficient in units of s–1 were calculated for a RO2 concentration of 1 × 109 molecules cm–3.
Of the studied cases, the fastest R′OOOR decomposition rates corresponded to systems where one of the reacting radicals is of the acetyl type and the other is of either an alkyl or β-oxo type (see Table 1). In these cases, the stability of the R′OOOR intermediate is relatively low, leading to rapid decomposition back into R′O2 + RO (or R′O + RO2) (see Figure 2a,b and Table 1). This is likely due to the resonance stabilization of the acetyloxy radical, which lowers the energy of this product channel. When both reactant radicals are of the acetyl type, the only decomposition channel possible for the R′OOOR intermediate is back into the parent reactants (shown in Figure 2c) as the acetyl RO2 can form neither a CI nor an aldehyde (due to the lack of H-atoms on the carbon atom containing the radical group). Note that CH3C(O)OO + CH3C(O)O will never occur in the atmosphere as the barrier for the decomposition of this acetyloxy radical into CH3 and CO2 has a barrier of only about ∼3 kcal/mol in zero-point corrected energies.7 The R′OOOR formed from the homo and hetero alkyl/β-oxo systems (see Figure 2d–f) is significantly more stable, and the rate of decomposition back to R′O2 + RO (or R′O + RO2) is accordingly slower (see Table 1). The most stable R′OOOR intermediate was found for the β-oxo-β-oxo system, which has a decomposition rate (at 298 K and 1 atm) of 1.5 × 10–2 s–1. The stability of R′OOOR adducts is thus in line with that of the analogous species R′OOR and R′OOOOR. While reactive, the former can have room-temperature lifetimes on the order of weeks or more, whereas the latter have been postulated since 1957 to be intermediates of RO2 + RO2 reactions but have such short lifetimes that they have, to our knowledge, never been experimentally detected.32,33
On the triplet surface, the R′O2 + RO product channels have significant barriers (see section S5). Similarly to the RO2 + OH reaction (section S1), reactions on the triplet surface would need to be essentially barrierless to be competitive with the rapid formation of the trioxide intermediates on the singlet surface. Given the calculated barrier heights reported here (several kcal/mol in zero-point corrected energy and over 10 kcal/mol in free energy), none of the studied product channels on the triplet surface are likely competitive.
Our results indicate that the R′O2 + RO reaction is a source of stable R′OOOR adducts. We estimated that the ambient steady-state concentrations of the adducts can range from 30 to 3 × 104 molecules cm–3 (see Table S5). Their stability was found to be strongly dependent on the structure of the reacting radicals that were considered, with decomposition rates ranging from a high of ∼50–100 s–1 for acetyl-alkyl and acetyl-β-oxo systems, respectively, and a low of ∼0.2–0.02 s–1 for the others. The binding energies (relative to R′O + RO2 and RO + R′O2) of R′OOOR adducts were computed at the ωB97X-D/6-31+G(d) level for a series of larger (4–10 C-atoms) RO and RO2 generated in the oxidation of representative anthropogenic and biogenic VOC molecules (see section S7). The computed R′OOOR stabilities were similar to those for the systems studied here (recomputed at the same level), indicating that the lifetimes of larger R′OOOR are also likely to be on the order of 10–100 s, in some cases (e.g., cyclohexene ozonolysis) possibly even higher. These stabilized adducts could therefore constitute a fraction of the low-volatile dimer compositions reported in ambient mass spectrometry measurements and are consequently important in SOA formation.
Methods
Quantum Chemical Calculations. To calculate the stationary points of the studied reactions, a systematic conformer search was performed for each system using MMFF34−39 implemented in the Spartan ’14 program.40 For the reactant and product systems in the RO2 + OH reaction, all conformers were optimized directly using density functional theory (DFT) at the ωB97X-D/aug-cc-pVTZ41−43 level due to the limited number of available conformers. For the R′OOOR intermediate complexes of the R′O2 + RO reaction, however, the conformers were first optimized at the lower DFT B3LYP/6-31+G(d) level,44−48 and those within 2 kcal/mol in relative electronic energies were selected for the higher-level optimization at the ωB97X-D/aug-cc-pVTZ level with the ultrafine integration grid. The transition state geometries connecting the different product channels studied here were found by performing a relaxed scan over the bond lengths of the appropriate atoms at the B3LYP/6-31+G(d) level of theory. The initial transition state optimization, as well as the intrinsic reaction coordinate (IRC) calculations to confirm that the transition states connected to the correct product channels, were performed at the same level. The transition states were subsequently reoptimized at the ωB97X-D/aug-cc-pVTZ level of theory. The electronic energies of the lowest-energy conformers of all reactants, intermediates, transition states, and products were corrected using ROHF-RCCSD(T)-F12a/VDZ-F12 single-point energies calculated with the Molpro program.49 We note that the ROHF-RCCSD(T)-F12a/VDZ-F12 correction to the formation energies of ROOOH and R′OOOR adducts were significant, making their formation more exergonic by ∼4 and ∼7–8 kcal/mol, respectively, relative to pure DFT energies.
RRKM Calculations. The master equation solver for multienergy well reactions (MESMER) program50 was used to calculate the Bartis–Widom51 phenomenological rate coefficients of the decomposition of the ROOOH and ROOOR intermediate complexes for the RO2 + OH and RO2 + RO reactions, respectively. Details of the MESMER program have been provided in detail by other authors in previous publications.52−55 MESMER uses the quantum chemically calculated zero-point corrected electronic energies, vibrational frequencies, and rotational constants. In addition, the program also requires the Lennard-Jones coefficients of the intermediate complex (ROOOH and R′OOOR) and the bath gas (N2) and the exponential down energy transfer parameter, ΔEdown, for the collisional energy transfer model for N2. Details of the MESMER simulations, conditions, and parameters used are provided in section S3.
Acknowledgments
The authors thank the Academy of Finland (266388,299574) for funding and the CSC IT Center for Science in Espoo, Finland, for computing resources.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00405.
Full computational details, log files of optimized reactants, intermediates, transition states and products containing the structures, energetics, vibrational frequencies, and rotational constants used in plotting the stationary points and running the MESMER simulations, details of the parameters used in MESMER simulations, pressure and temperature dependencies of formation rates of ROOOH and ROOOR intermediates and an example MESMER input file (PDF)
Molpro log and out files containing the ROHF-RCCSD(T)-F12a/VDZ-F12 single-point electronic energies (ZIP)
The authors declare no competing financial interest.
Supplementary Material
References
- Ehn M.; Thornton J. A.; Kleist E.; Sipilä M.; Junninen H.; Pullinen I.; Springer M.; Rubach F.; Tillmann R.; Lee B.; et al. A Large Source of Low-Volatility Secondary Organic Aerosol. Nature 2014, 506, 476–479. 10.1038/nature13032. [DOI] [PubMed] [Google Scholar]
- Mentel T. F.; Springer M.; Ehn M.; Kleist E.; Pullinen I.; Kurtén T.; Rissanen M.; Wahner A.; Wildt J. Formation of Highly Oxidized Multifunctional Compounds: Autoxidation of Peroxy Radicals Formed in the Ozonolysis of Alkenes - Deduced from Structure-Product Relationships. Atmos. Chem. Phys. 2015, 15, 6745–6765. 10.5194/acp-15-6745-2015. [DOI] [Google Scholar]
- Berndt T.; Richters S.; Kaethner R.; Voigtländer J.; Stratmann F.; Sipilä M.; Kulmala M.; Herrmann H. Gas-Phase Ozonolysis of Cycloalkenes: Formation of Highly Oxidized RO2 Radicals and Their Reactions With NO, NO2, SO2, and Other RO2 Radicals. J. Phys. Chem. A 2015, 119, 10336–10348. 10.1021/acs.jpca.5b07295. [DOI] [PubMed] [Google Scholar]
- Rissanen M. P.; Kurtén T.; Sipilä M.; Thornton J. A.; Kangasluoma J.; Sarnela N.; Junninen H.; Jørgensen S.; Schallhart S.; Kajos M. K.; et al. The Formation of Highly Oxidized Multifunctional Products in the Ozonolysis of Cyclohexene. J. Am. Chem. Soc. 2014, 136, 15596–15606. 10.1021/ja507146s. [DOI] [PubMed] [Google Scholar]
- Peeters J.; Nguyen T. L.; Vereecken L. HOx Radical Regeneration in the Oxidation of Isoprene. Phys. Chem. Chem. Phys. 2009, 11, 5935–5939. 10.1039/b908511d. [DOI] [PubMed] [Google Scholar]
- Asatryan R.; da Silva G.; Bozzelli J. W. Quantum Chemical Study of the Acrolein (CH2CHCHO) + OH + O2 Reactions. J. Phys. Chem. A 2010, 114, 8302–8311. 10.1021/jp104828a. [DOI] [PubMed] [Google Scholar]
- Vereecken L.; Peeters J. Decomposition of Substituted Alkoxy Radicals - Part I: A Generalized Structure-Activity Relationship for Reaction Barrier Heights. Phys. Chem. Chem. Phys. 2009, 11, 9062–9074. 10.1039/b909712k. [DOI] [PubMed] [Google Scholar]
- Archibald A. T.; Petit A. S.; Percival C. J.; Harvey J. N.; Shallcross D. E. On the Importance of the Reaction Between OH and RO2 Radicals. Atmos. Sci. Lett. 2009, 10, 102–108. 10.1002/asl.216. [DOI] [Google Scholar]
- Fittschen C.; Whalley L. K.; Heard D. E. The Reaction of CH3O2 Radicals with OH Radicals: A Neglected Sink for CH3O2 in the Remote Atmosphere. Environ. Sci. Technol. 2014, 48, 7700–7701. 10.1021/es502481q. [DOI] [PubMed] [Google Scholar]
- Bossolasco A.; Faragó E. P.; Schoemaecker C.; Fittschen C. Rate Constant of the Reaction Between CH3O2 Radicals and OH Radicals. Chem. Phys. Lett. 2014, 593, 7–13. 10.1016/j.cplett.2013.12.052. [DOI] [PubMed] [Google Scholar]
- Assaf E.; Song B.; Tomas A.; Schoemaecker C.; Fittschen C. Rate Constant of the Reaction Between CH3O2 Radicals and OH Radicals Revisited. J. Phys. Chem. A 2016, 120, 8923–8932. 10.1021/acs.jpca.6b07704. [DOI] [PubMed] [Google Scholar]
- Yan C.; Kocevska S.; Krasnoperov L. N. Kinetics of the Reaction of CH3O2 Radicals with OH Studied Over the 292–526 K Temperature Range. J. Phys. Chem. A 2016, 120, 6111–6121. 10.1021/acs.jpca.6b04213. [DOI] [PubMed] [Google Scholar]
- Müller J.-F.; Liu Z.; Nguyen V. S.; Stavrakou T.; Harvey J. N.; Peeters J. The Reaction of Methyl Peroxy and Hydroxyl Radicals as a Major Source of Atmospheric Methanol. Nat. Commun. 2016, 7, 13213. 10.1038/ncomms13213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian H.; Zhang S.; Zhang H. Theoretical Study on the Atmospheric Reaction of CH3O2 with OH. Int. J. Quantum Chem. 2015, 115, 1181–1186. 10.1002/qua.24946. [DOI] [Google Scholar]
- Liu Y.; Chen L.; Chen D.; Wang W.; Liu F.; Wang W. Computational Study on Mechanisms of C2H5O2 + OH Reaction and Properties of C2H5O3H complex. Chem. Res. Chin. Univ. 2017, 33, 623–630. 10.1007/s40242-017-7055-4. [DOI] [Google Scholar]
- Caravan R. L.; Khan M. A. H.; Zádor J.; Sheps L.; Antonov I. O.; Rotavera B.; Ramasesha K.; Au K.; Chen M.-W.; Rösch D.; et al. The Reaction of Hydroxyl and Methylperoxy Radicals is Not a Major Source of Atmospheric Methanol. Nat. Commun. 2018, 9, 4343–4352. 10.1038/s41467-018-06716-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf E.; Tanaka S.; Kajii Y.; Schoemaecker C.; Fittschen C. Rate Constants of the Reaction of C2-C4 Peroxy Radicals with OH Radicals. Chem. Phys. Lett. 2017, 684, 245–249. 10.1016/j.cplett.2017.06.062. [DOI] [Google Scholar]
- Assaf E.; Sheps L.; Whalley L.; Heard D.; Tomas A.; Schoemaecker C.; Fittschen C. The Reaction Between CH3O2 and OH Radicals. Product Yields and Atmospheric Implications. Environ. Sci. Technol. 2017, 51, 2170–2177. 10.1021/acs.est.6b06265. [DOI] [PubMed] [Google Scholar]
- Assaf E.; Schoemaecker C.; Vereecken L.; Fittschen C. Experimental and Theoretical Investigation of the Reaction of RO2 Radicals with OH Radicals: Dependence of the HO2 Yield on the Size of the Alkyl Group. Int. J. Chem. Kinet. 2018, 50, 670–680. 10.1002/kin.21191. [DOI] [Google Scholar]
- Hasson A. S.; Kuwata K. T.; Arroyo M. C.; Petersen E. B. Theoretical Studies of the Reaction of Hydroperoxy Radicals (HO2) With Ethyl Peroxy (CH3CH2O2), Acetyl Peroxy (CH3C(O)O2), and Acetonyl Peroxy (CH3C(O)CH2O2) Radicals. J. Photochem. Photobiol., A 2005, 176, 218–230. 10.1016/j.jphotochem.2005.08.012. [DOI] [Google Scholar]
- Mohr C.; Lopez-Hilfiker F. D.; Yli-Juuti T.; Heitto A.; Lutz A.; Hallquist M.; D’Ambro E. L.; Rissanen M. P.; Hao L.; Schobesberger S.; et al. Ambient Observations of Dimers From Terpene Oxidation in the Gas-Phase: Implications For New Particle Formation and Growth. Geophys. Res. Lett. 2017, 44, 2958–2966. 10.1002/2017GL072718. [DOI] [Google Scholar]
- Tröstl J.; Chuang W. K.; Gordon H.; Heinritzi M.; Yan C.; Molteni U.; Ahlm L.; Frege C.; Bianchi F.; Wagner R.; et al. The Role of Low-Volatility Organic Compounds in Initial Particle Growth in the Atmosphere. Nature 2016, 533, 527–531. 10.1038/nature18271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahnt A.; Vermeylen R.; Iinuma Y.; Safi Shalamzari M.; Maenhaut W.; Claeys M. High-Molecular-Weight Esters in α-Pinene Ozonolysis Secondary Organic Aerosol: Structural Characterization and Mechanistic Proposal for their Formation from Highly Oxygenated Molecules. Atmos. Chem. Phys. 2018, 18, 8453–8467. 10.5194/acp-18-8453-2018. [DOI] [Google Scholar]
- Rissanen M. P.; Kurtén T.; Sipilä M.; Thornton J. A.; Kausiala O.; Garmash O.; Kjaergaard H. G.; Petäjä T.; Worsnop D. R.; Ehn M.; et al. Effects of Chemical Complexity on the Autoxidation Mechanisms of Endocyclic Alkene Ozonolysis Products: From Methylcyclohexenes Toward Understanding α-Pinene. J. Phys. Chem. A 2015, 119, 4633–4650. 10.1021/jp510966g. [DOI] [PubMed] [Google Scholar]
- Ehn M.; Kleist E.; Junninen H.; Petäjä T.; Lönn G.; Schobesberger S.; Dal Maso M.; Trimborn A.; Kulmala M.; Worsnop D. R.; et al. Gas Phase Formation of Extremely Oxidized Pinene Reaction Products in Chamber and Ambient Air. Atmos. Chem. Phys. 2012, 12, 5113–5127. 10.5194/acp-12-5113-2012. [DOI] [Google Scholar]
- Krapf M.; El Haddad I.; Bruns E. A.; Molteni U.; Daellenbach K. R.; Prévôt A. S.; Baltensperger U.; Dommen J. Labile Peroxides in Secondary Organic Aerosol. Chem. 2016, 1, 603–616. 10.1016/j.chempr.2016.09.007. [DOI] [Google Scholar]
- Zhao J.; Ortega J.; Chen M.; McMurry P. H.; Smith J. N. Dependence of Particle Nucleation and Growth on High-Molecular-Weight Gas-Phase Products During Ozonolysis of α-Pinene. Atmos. Chem. Phys. 2013, 13, 7631–7644. 10.5194/acp-13-7631-2013. [DOI] [Google Scholar]
- Long B.; Bao J. L.; Truhlar D. G. Atmospheric Chemistry of Criegee Intermediates: Unimolecular Reactions and Reactions with Water. J. Am. Chem. Soc. 2016, 138, 14409–14422. 10.1021/jacs.6b08655. [DOI] [PubMed] [Google Scholar]
- Johnson D.; Marston G. The Gas-Phase Ozonolysis of Unsaturated Volatile Organic Compounds in the Troposphere. Chem. Soc. Rev. 2008, 37, 699–716. 10.1039/b704260b. [DOI] [PubMed] [Google Scholar]
- Vereecken L. Lifting the Veil on an Old Mystery. Science 2013, 340, 154–155. 10.1126/science.1236475. [DOI] [PubMed] [Google Scholar]
- Taatjes C. A.; Shallcross D. E.; Percival C. Research Frontiers in the Chemistry of Criegee Intermediates and Tropospheric Ozonolysis. Phys. Chem. Chem. Phys. 2014, 16, 1704–1718. 10.1039/c3cp52842a. [DOI] [PubMed] [Google Scholar]
- Russell G. A. Deuterium-Isotope Effects in the Autoxidation of Aralkyl Hydrocarbons. Mechanism of the Interaction of Peroxy Radicals. J. Am. Chem. Soc. 1957, 79, 3871–3877. 10.1021/ja01571a068. [DOI] [Google Scholar]
- Howard J. A.; Ingold K. U. Self-Reaction of Sec-Butylperoxy Radicals. Confirmation of the Russell Mechanism. J. Am. Chem. Soc. 1968, 90, 1056–1058. 10.1021/ja01006a037. [DOI] [Google Scholar]
- Halgren T. A. Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. . [DOI] [Google Scholar]
- Halgren T. A. Merck Molecular Force Field. II. MMFF94 Van Der Waals and Electrostatic Parameters for Intermolecular Interactions. J. Comput. Chem. 1996, 17, 520–552. . [DOI] [Google Scholar]
- Halgren T. A. Merck Molecular Force Field. III. Molecular Geometries and Vibrational Frequencies for MMFF94. J. Comput. Chem. 1996, 17, 553–586. . [DOI] [Google Scholar]
- Halgren T. A.; Nachbar R. B. Merck Molecular Force Field. IV. Conformational Energies and Geometries for MMFF94. J. Comput. Chem. 1996, 17, 587–615. . [DOI] [Google Scholar]
- Halgren T. A. Merck Molecular Force Field. V. Extension of MMFF94 Using Experimental Data, Additional Computational Data, and Empirical Rules. J. Comput. Chem. 1996, 17, 616–641. . [DOI] [Google Scholar]
- Halgren T. A. MMFF VII. Characterization of MMFF94, MMFF94s, and Other Widely Available Force Fields for Conformational Energies and for Intermolecular-Interaction Energies and Geometries. J. Comput. Chem. 1999, 20, 730–748. . [DOI] [PubMed] [Google Scholar]
- Spartan ’14; Wavefunction Inc.: Irvine, CA, 2014.
- Chai J. D.; Head-Gordon M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- Dunning T. H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Kendall R. A.; Dunning T. H.; Harrison R. J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. 10.1063/1.462569. [DOI] [Google Scholar]
- Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Lee C.; Yang W.; Parr R. H. Development of the Colle-Salvetti Correlation-Energy Formula Into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Hehre W. J.; Ditchfield R.; Pople J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
- Clark T.; Chandrasekhar J.; Spitznagel G. W.; Schleyer P. v. R. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. 10.1002/jcc.540040303. [DOI] [Google Scholar]
- Frisch M. J.; Pople J. A.; Binkley J. S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. 10.1063/1.447079. [DOI] [Google Scholar]
- Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M.; Celani P.; Korona T.; Lindt R.; Mitrushenkov A.; Rauhut G.; et al. MOLPRO, version 2015.1, A Package of Ab Initio Programs; 2015; see http://www.molpro.net (Retrieved Apr 1, 2019).
- Glowacki D. R.; Liang C.-H.; Morley C.; Pilling M. J.; Robertson S. H. MESMER: Open-Source Master Equation Solver for Multi-Energy Well Reactions. J. Phys. Chem. A 2012, 116, 9545–9560. 10.1021/jp3051033. [DOI] [PubMed] [Google Scholar]
- Bartis J. T.; Widom B. Stochastic Models of the Interconversion of Three or More Chemical Species. J. Chem. Phys. 1974, 60, 3474–3482. 10.1063/1.1681562. [DOI] [Google Scholar]
- Carr S. A.; Still T. J.; Blitz M. A.; Eskola A. J.; Pilling M. J.; Seakins P. W.; Shannon R. J.; Wang B.; Robertson S. H. Experimental and Theoretical Study of the Kinetics and Mechanism of the Reaction of OH Radicals with Dimethyl Ether. J. Phys. Chem. A 2013, 117, 11142–11154. 10.1021/jp4070278. [DOI] [PubMed] [Google Scholar]
- Carr S. A.; Glowacki D. R.; Liang C. H.; Baeza-Romero M. T.; Blitz M. A.; Pilling M. J.; Seakins P. W. Experimental and Modeling Studies of the Pressure and Temperature Dependences of the Kinetics and the OH Yields in the Acetyl + O2 Reaction. J. Phys. Chem. A 2011, 115, 1069–1085. 10.1021/jp1099199. [DOI] [PubMed] [Google Scholar]
- Shannon R. J.; Tomlin A. S.; Robertson S. H.; Blitz M. A.; Pilling M. J.; Seakins P. W. Global Uncertainty Propagation and Sensitivity Analysis in the CH3OCH2 + O2 System: Combining Experiment and Theory To Constrain Key Rate Coefficients in DME Combustion. J. Phys. Chem. A 2015, 119, 7430–7438. 10.1021/acs.jpca.5b00620. [DOI] [PubMed] [Google Scholar]
- Stone D.; Au K.; Sime S.; Medeiros D. J.; Blitz M.; Seakins P. W.; Decker Z.; Sheps L. Unimolecular Decomposition Kinetics of the Stabilized Criegee Intermediates CH2OO and CD2OO. Phys. Chem. Chem. Phys. 2018, 20, 24940–24954. 10.1039/C8CP05332D. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.