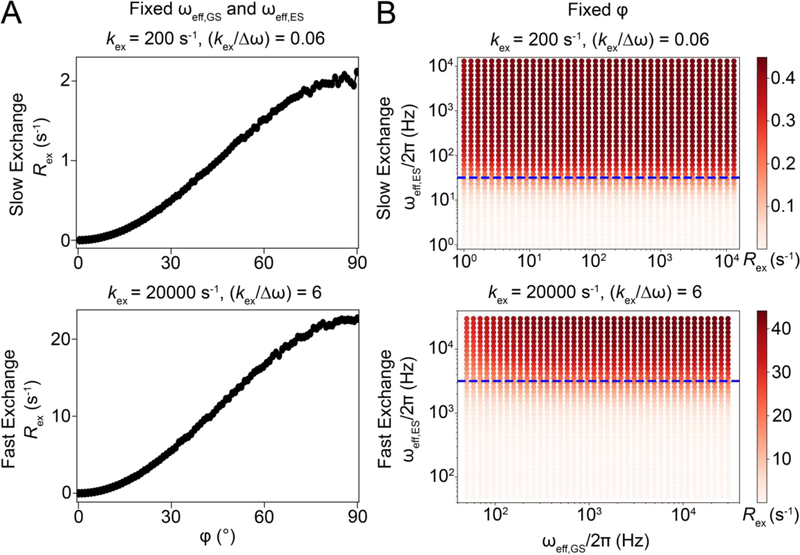
Figure 15.

Vector model simulations to illustrate the dependence of R_ex on φ, ω_eff,GS and ω_eff,ES during an on-resonance R_1ρ experiment for a system undergoing two-state GS-ES exchange. A) Variation of R_ex with φ for a fixed ω_eff,GS and ω_eff,ES, under fast and slow exchange conditions. Simulations were performed using ω_eff,GS = 1000*2π rad s⁻¹ and ω_eff,ES = 1131*2π rad s⁻¹ when on-resonance with the GS under slow exchange conditions. ω_eff,GS = 1000*2π rad s⁻¹ and ω_eff,ES = 1128*2π rad s⁻¹ under fast exchange conditions while maintaining the AVG state onresonance by suitably adjusting the offset of the GS and ES. Similar trends are observed for alternative values of the precession frequencies (data not shown). B) Heat maps of R_ex as a function of ω_eff,GS and ω_eff,ES for a fixed φ under fast and slow exchange conditions. Horizontal dotted lines (blue) correspond to the condition ω_eff,ES = k_ex. Orientations of the effective fields were kept fixed at those corresponding to application of ω₁/2π = 1000 Hz on resonance. Similar trends are also observed for R_1ρ, and for both R_ex and R_1ρ under off-resonance conditions, as long as the magnetization decay is mono-exponential (data not shown). For panels A and B, simulations were performed using 10,000 spins with p_ES = 0.01, $\Delta \overline{\omega }{(}^{13}\text{C)}=3\text{\hspace{0.17em}ppm}$, γ(¹H)B₀/2π = 700 MHz, R_1,GS= R_1,ES = 0.0 s⁻¹, R_2,GS = R_2,ES = 0.0 s⁻¹. The relaxation delays used were 3 s and 0.6 s for k_ex = 200 and 20000 s⁻¹, respectively. For both panels, the initial alignment of magnetization and its projection to calculate R_ex, was performed as described in Section 6.1.