Table 1.

Principal definitions, symbols, and default parameter values used in equations

Symbol	Identification	Definition/values used
N	Number of neurons in network	3000 (24,000 in some network simulations)
k	Number of synapses per neuron	30 (for CA1), 90 (for CA3)
s	Spontaneous firing rate of a single neuron per time step of size τd	0.0315 × τd
τR	Absolute refractory time of neuron	28 msec (IF), 36 msec (Poiss, HH)
τd	Synaptic time delay	2.8 msec (IF), 3.7 msec (Poiss), 1-5 msec (HH)
ρ	Proportion of long-distance connections generated by breaking a synapse and rewiring it to a randomly chosen postsynaptic cell	Varied from 1.0 × 10−5 to 0.4
p1	Synaptic strength (i.e., probability that postsynaptic neuron will fire given that a particular presynaptic neuron fired)	0.025
p2	Probability that two postsynaptic neurons fire given the presynaptic neuron fired (dependent on k and p1)	p2 = 1 - (1 - p1)k - kp1(1 - p1)k−1
α	Approximate number of neurons in wave front	k/2 - 1
R	Number of time steps that a neuron remains refractory	R = τR/τd ≈ 10
Wi	Number of waves present in network at time i	Wi + 1 = f(Wi)
ei	Number of excitable neurons in the network at time i	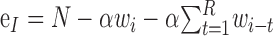or ei = N − αwi(1+R) (for one-dimensional map)
ni	Number of new waves generated at time i resulting from long-distance connections	ni = (2αWi kρ)(p1p2ei/N) + Si
di	Number of waves that die in time step i resulting from wave collision	di = 2αWi/ei
Si	Spontaneous wave generation resulting from spontaneous cellular activity	Si = seip2
W*	Number of waves in network where new wave rate and dying wave rate are equal (equilibrium point)	f(W*) = W*
f(Wi)	Function describing number of waves on next time step given number of waves on time step i	f(Wi) = Wi + ni − di