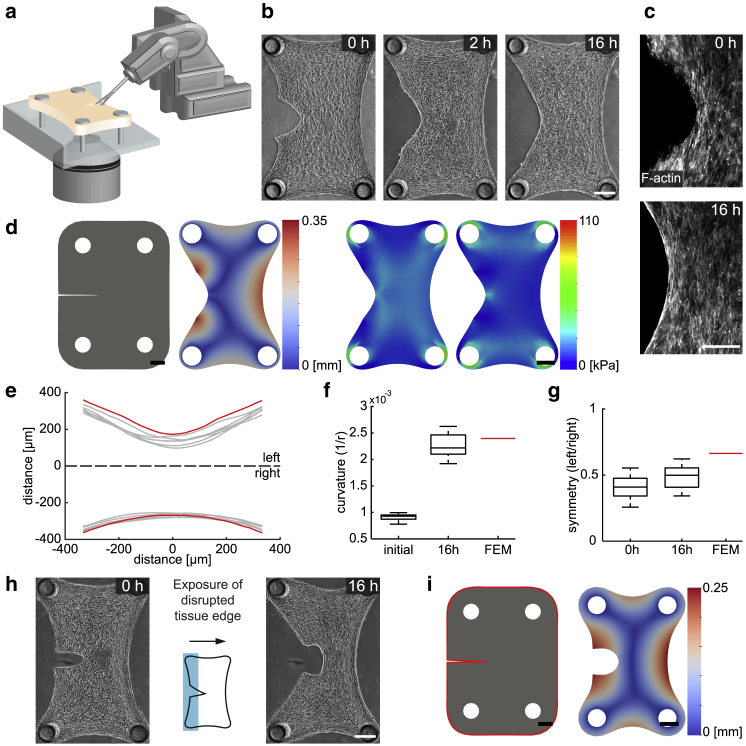
Figure 4.

Surface stresses drive restoration at the tissue periphery. (a) A schematic illustration of the cutting of tissues using the actuated microscissors mounted on the robotic platform is given. (b) Temporal sequence of micrographs showing the morphological changes after the cut is shown. (c) Immunofluorescence optical section of a microtissue showing the filamentous actin is given. The cellular contractility at the periphery smooths the rough edges. (d) Finite-element simulations of a microtissue with a thin notch on its side are shown. Displacement map (left) and simulated distribution of principal stress (right) are shown at the equilibrium state. (e) The full set of reconstructed microtissue boundaries 16 h after surgical intervention (gray, n = 6) are shown along with the prediction of the simulation (red). (f) A box plot showing curvature at the operated side of the microtissue (n = 12) is given. The red line shows the predicted curvature. (g) A box plot showing the symmetry of microtissues with respect to the longitudinal axis (n = 12) is given. The red line shows the predicted symmetry. (h) Phototoxic inactivation of cells at the disrupted boundary is shown. Representative images are from before and 16 h after treatment. The schematic shows the exposed area (shaded in blue). (i) Finite-element simulation of a cut microtissue is shown. The surface contractile modulus on the periphery of the microtissue is set to zero throughout the simulation (highlighted in red). Scale bars, 150 μm. To see this figure in color, go online.