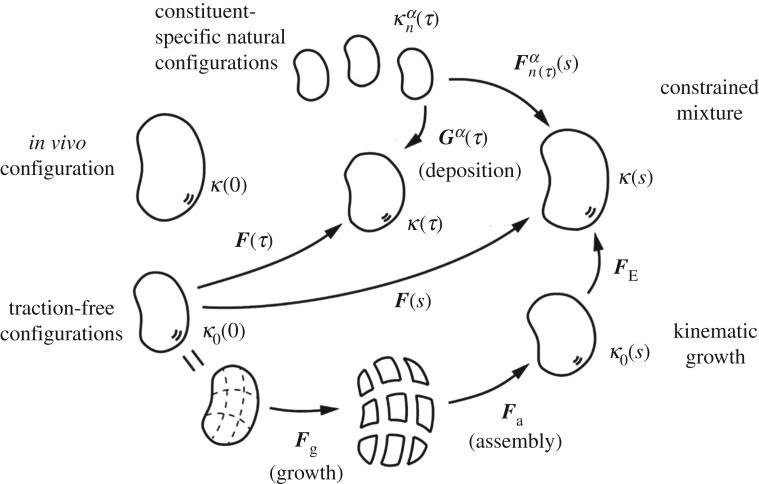
Figure 2.

Schematic drawing of evolving configurations of importance in both a theory of finite kinematic growth (bottom portion) and a constrained mixture theory (top portion). In particular, note the common reference κ_o(0) and current κ(s) configurations. In the kinematic growth theory, one imagines that infinitesimal stress-free portions of the body grow independently via the transformation ${\mathit{F}}^{\mathrm{g}}$, which need not result in compatible growth. An elastic ‘assembly’ transformation ${\mathit{F}}^{\mathrm{a}}$ ensures a contiguous traction-free body, which typically is residually stressed. Finally, an elastic load-dependent transformation ${\mathit{F}}^{\mathrm{E}}$ yields the current configuration of interest, with ${\mathit{F}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{E}}\cdot {\mathit{F}}^{\mathrm{a}}$ that part of the deformation that is elastic and determines the stress field. Conversely, in the constrained mixture theory, it is the constituent-specific deformation ${\mathit{F}}_{n(\tau )}^{\alpha }$ from an individual stress-free configuration that dictates the elastic stress within that constituent. It is easy to show that ${\mathit{F}}_{n(\tau )}^{\alpha }(s)=\mathit{F}(s)\cdot {\mathit{F}}^{-1}(\tau )\cdot {\mathit{G}}^{\alpha }(\tau )$, where ${\mathit{G}}^{\alpha }(\tau )$ is a so-called ‘deposition stretch’ tensor that accounts for cells depositing new extracellular matrix under stress when incorporating it within stressed extant matrix. Both approaches require multiplicative deformations, one in terms of the prescribed growth of stress-free elements and one in terms of a deformation that is built into individual constituents when they are incorporated within extant tissue.