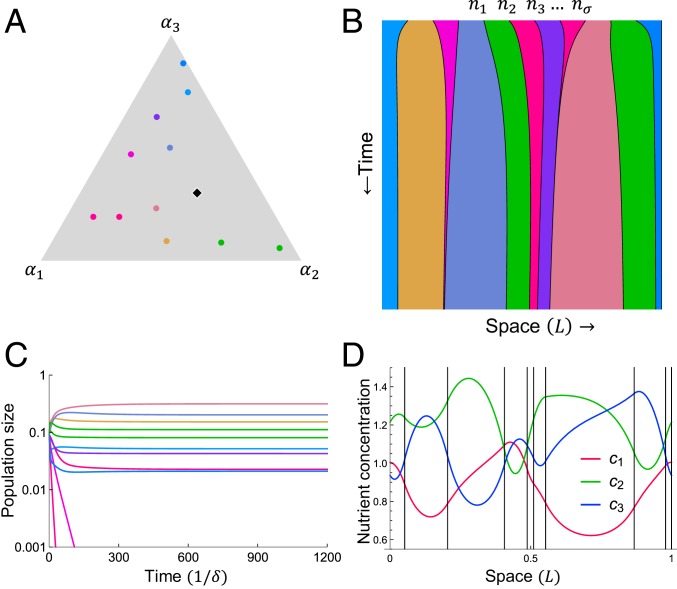
Fig. 1.

A model with spatial structure and metabolic trade-offs supports more species than expected from the principle of competitive exclusion. Example with 3 nutrients and 11 species starting with equal populations is shown. (A) Each species uptakes nutrients according to its enzyme-allocation strategy $\left({\alpha }_{\sigma 1},{\alpha }_{\sigma 2},{\alpha }_{\sigma 3}\right)$. Because strategies satisfy the budget constraint ${\sum }_i{\alpha }_{\sigma i}=E$, each can be represented as a point on a triangle in strategy space. The nutrient supply $\overrightarrow{s}=\left(E/S\right)\overrightarrow{S}=\left(0.25,0.45,0.3\right)$ is represented as a black diamond. Colors correspond to strategies and are consistent throughout the figure. (B) Each species occupies a fraction of a 1-dimensional space (a ring) and has a corresponding time-dependent population size $n_{\sigma }\left(t\right)$. Here, the nutrient diffusion time ${\tau }_D$ is 400. (C) Population dynamics from A. Nine species coexist on 3 nutrients. (D) Concentrations of the 3 nutrients at steady state (vertical black lines denote boundaries between populations).