Flow Arrest in the Plasma Membrane

Abstract

The arrangement of receptors in the plasma membrane strongly affects the ability of a cell to sense its environment both in terms of sensitivity and in terms of spatial resolution. The spatial and temporal arrangement of the receptors is affected in turn by the mechanical properties and the structure of the cell membrane. Here, we focus on characterizing the flow of the membrane in response to the motion of a protein embedded in it. We do so by measuring the correlated diffusion of extracellularly tagged transmembrane neurotrophin receptors TrkB and p75 on transfected neuronal cells. In accord with previous reports, we find that the motion of single receptors exhibits transient confinement to submicron domains. We confirm predictions based on hydrodynamics of fluid membranes, finding long-range correlations in the motion of the receptors in the plasma membrane. However, we discover that these correlations do not persist for long ranges, as predicted, but decay exponentially, with a typical decay length on the scale of the average confining domain size.

Significance

The plasma membrane is the interface through which a cell interacts with its environment. Membrane proteins function both as mechanical and chemical signal sensors, transmitting the information they receive into the cell via cascades of biochemical reactions. To optimize its response and adaptation to external conditions, a cell may control the spread of the plasma membrane proteins, for example, in dispersed nanoclusters. Understanding the mechanism and strategy of such protein self-organization requires the knowledge of the material properties of the cell membrane and the mobility of proteins and lipids within the membrane. Here, we show long-range correlations in the motion of membrane proteins. However, contrary to belief, we show that the plasma membrane does not flow as a continuous fluid at long range.

Main Text

The plasma membrane is a highly dynamic heterogeneous object. It is made of a lipid bilayer in which a variety of proteins are embedded and is anchored to the cytoskeleton through binding domains (1, 2, 3, 4, 5, 6). Although the weight percent of lipids and proteins in the plasma membrane is comparable, the conventional description of the plasma membrane is of a complex fluid in which protein inclusions can diffuse (7). This point of view is supported by the observed mobility of entities of different sizes embedded in the plasma membrane, such as protein aggregates and transient lipid rafts (6, 7, 8, 9, 10). For this reason, models such as the Saffman-Delbrück model (11) that describe the plasma membrane as a simple viscous fluid are often inconsistent with experimental observations. For example, a significantly lower mobility of proteins is measured in live cells as compared to in artificial lipid-based vesicles that are composed of a fluid lipid bilayer (3, 8) and in red blood cells (12). The question then arises regarding whether a membrane that is “more mosaic than fluid” (3) can flow like a fluid lipid bilayer. Continuous flow of the plasma membrane is believed to be the mechanism for fast equilibration of membrane tension. Such flow is therefore essential for the commonly suggested mediation of fast long-range mechanical signals within cells (e.g., see (13, 14, 15, 16, 17, 18, 19, 20) and reference in (21)). Surprisingly, a recent study by Shi et al. (21) has put forth evidence that local changes in the cell membrane tension result in localized mechanical signaling. In these experiments, short tethers where pulled out of cells to perturb locally the tension in the cell membrane and to measure it. No mechanical coupling between two tethers drawn at distances of 5–15 μm was observed in contrast to the strong coupling found for tethers drawn from cell-attached membrane blebs. To account for their findings, the authors suggest a model in which the membrane has a gel-like structure and that transmembrane proteins anchored to the cytoskeleton are the source of the membrane’s resistance to flow.

The correlated motion of tracer particle gives a direct measure of fluid flow. It was proposed and used to characterize the viscoelastic properties of complex fluids (22, 23, 24) in microscopic length scales. In this method, the effect of the mechanical perturbation created by the thermal motion of one tracer on the motion of a second tracer is measured as a function of their separation. For correlations between the motion of the two tracers in a membrane to exist, information through flow or deformation of the membrane needs to pass between them (24, 25, 26, 27, 28). As a result, the correlated motion is not only a means to characterize the viscoelastic properties of a complex fluid at large length scales, which are larger than the scale of structural and compositional inhomogeneity in it, but also a way to characterize the relevant length scale of heterogeneity (23, 25, 29). This measurement is insensitive to tracer size or to tracer confinement as long as the material in which the tracer is suspended can flow or deform (24, 30).

Here, we use single-particle tracking of transmembrane proteins diffusing on the plasma membrane of two types of cells to extract the characteristic flow of the plasma membrane. From this direct measurement, we quantify the characteristic flow of the plasma membrane and its range before being arrested. Our results further support and provide new, to our knowledge, insight into the surprising results of Shi et al. (21).

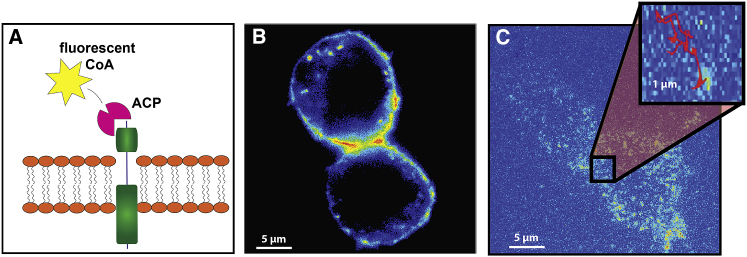
Our experiments consisted of imaging the motion of TrkB and p75 receptors along the plasma membrane of neuronal and HEK 293T cells. In each experiment, we follow only one of the two receptors. The receptors were tagged extracellularly using ACP-CoA surface labeling, previously described in (31) (Fig. 1, A and B), resulting in minimal background noise arising from the cell cytoplasm. Importantly, the tagged receptors keep their biological function and specificity (see Supporting Materials and Methods; (31)). We use TIRF to image the motion of these receptors on the cell membrane on a single molecule level (Fig. 1 C) and extract their motion using video microscopy (32) (see details in Supporting Materials and Methods). To obtain significant statistics, we analyze more than 40,000 trajectories, each of them longer than 20 frames (i.e., at least 0.5 s long), from at least 40 different cells from several independent cultures for each receptor and cell type.

Figure 1.

Experimental system. (A) A schematic representation of the TrkB receptor and its fluorescent tagging are shown. (B) An oblique illumination image of transfected primary motor neuron shows that TrkB ACP is localized on the cell membrane. (C) Single TrkB receptors on the cell membrane of a motor neuron as imaged by TIRF are shown. To see this figure in color, go online.

From the extracted trajectory of the receptors, we calculate the correlated displacement of two proteins α and β according to the following:

$$D_{\left|\right|,\perp }\left(R,\tau \right)={\langle \mathit{\Delta }{r}_{\left|\right|,\perp }^{\alpha }\left(\text{τ}\right)\mathit{\Delta }{r}_{\left|\right|,\perp }^{\beta }\left(\tau \right)\delta \left(|{\overrightarrow{r}}^{\alpha \beta }\text{|}-R\right)\rangle }_{\alpha \ne \beta }$$ (1)

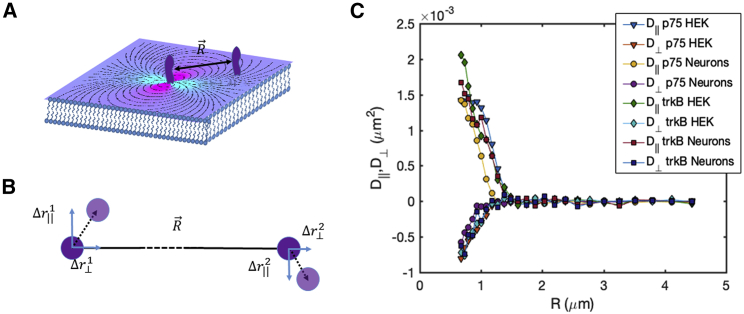
where ${\overrightarrow{r}}^{\alpha \beta }$ is the vector connecting the two proteins, $\mathit{\Delta }{r}_{\left|\right|,\perp }^{\alpha ,\beta }$ is the displacement of protein α, or β along the direction parallel or perpendicular to ${\overrightarrow{r}}^{\alpha \beta }$, and δ(r) is the δ function (for discussion on measurement errors, see Supporting Materials and Methods). The correlated displacement of both receptors, TrkB and p75, in both cell types with τ = 25 ms is presented in Fig. 2. Each cell contained only one type of tagged receptors; therefore, correlations in motion were calculated only between receptors of the same type.

Figure 2.

Two-point microrheology of transmembrane proteins in the plasma membrane. (A) An illustration of two proteins embedded in the plasma membrane at a distance R ρ is shown. The dotted lines represent the flow field induced by the motion of the protein in the center of the image. (B) Cross correlation between displacements along the line connecting the proteins and the line perpendicular to them are calculated. (C) The measured correlated diffusion of p75 and TrkB in neurons and in HEK cells as a function of distance is shown. All the results fall on the same lines, confirming the similar flow characteristics of the plasma membrane in response to the different proteins and in the different cell types. To see this figure in color, go online.

The flow generated by the motion of a protein in the membrane affects the motion of a second protein at a distance r from it and vice versa. This information exchange is manifested in correlations in the motion of the proteins in the membrane. For example, in a membrane with mobile protein inclusions suspended in fluid, for protein separations larger than the protein diameter, $r\gg a$, we expect $D_{\left|\right|}\sim r^{-1},D_{\perp }\sim r^{-2}$ (26). However, if the membrane is supported on a glass surface, which is the case in total internal reflection fluorescence (TIRF) microscopy, for large separations, we expect $D_{\left|\right|,\perp }\cong \pm k_{B}Th/2\pi {\eta }_f{r}^2$, where k_BT is the thermal energy, h is the distance between the membrane and the supporting surface, and ${\eta }_f$ is the viscosity of the surrounding fluid (33). This result is the asymptotic behavior expected in the case of an adsorbed membrane on a glass surface at large separation between tracer particles (33). Similarly, immobile inclusions in the plasma membrane will cause the correlated diffusion in both directions to decay at large separations as r⁻² (34). The flow field induced by a protein in this case is depicted by the dotted lines in Fig. 2 A.

From the theoretical analysis, for our experimental conditions, we expect the long-range correlated diffusion in the parallel and transverse direction of both receptors and in the different cell types to agree well (Fig. 2 C). As predicted theoretically, the symmetry of the flow field causes the longitudinal response to be positive and the transverse response to be negative. To compare these measurement to the theoretical prediction of Oppenheimer and Diamant (33), we estimated the parameters entering the calculation as follows: the distance of the plasma membrane to the glass slide to be h = 50 nm (35, 36), the thickness of the plasma membrane to be w = 4 nm (37), the radius of the transmembrane part of the receptors to be a = 2 nm, the viscosity of the cytosol and surrounding medium to be equal and ${\eta }_F=0.001$ Pa ⋅ s (similar to water), and the viscosity of membrane ${\eta }_m=0.395$ Pa ⋅ s (37).

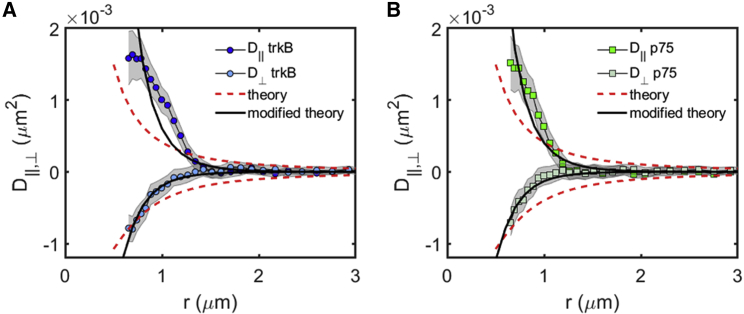
The calculated correlated diffusion agrees well with the experimentally measured one for both receptors, with positive longitudinal correlations and negative transverse correlation (Fig. 3). Surprisingly, these correlations seem to decay much faster than expected. To account for this discrepancy, we modify the theoretical prediction by multiplying the transverse and longitudinal solutions with the same exponentially decaying function. This fit provides us with an estimate for a typical decay length of the correlations, which in our case is 450 ± 80 nm (Fig. 3, A and B). The flow of the plasma membrane is completely arrested, namely, correlations decay to the noise level, on length scales larger than 1.7 ± 0.2 μm, as seen in Fig. 3. We note that the fact that the membrane flow is arrested at large distances does not imply that proteins and other biomolecules cannot diffuse in between domains. These findings indicate that the motion of proteins in the plasma membrane is strongly correlated at intermediate distances (∼450 nm) via the flow field induced in the membrane by their motion. However, at larger distances (∼1.5 μm and larger) the motion of proteins is completely decoupled.

Figure 3.

Correlated diffusion of protein receptors on the plasma membrane of neuronal cells exhibit long-range correlations. Comparisons between the correlated diffusion of TrkB (A) and p75 (B) in the longitudinal and transverse directions are shown. Similar behavior is observed for both receptors, with a qualitative agreement with the simplified theory of (33) (red dashed line; see text for the parameter choice for the theoretical curves). The modified theory (black solid line) better fits the experimental results of both proteins. To see this figure in color, go online.

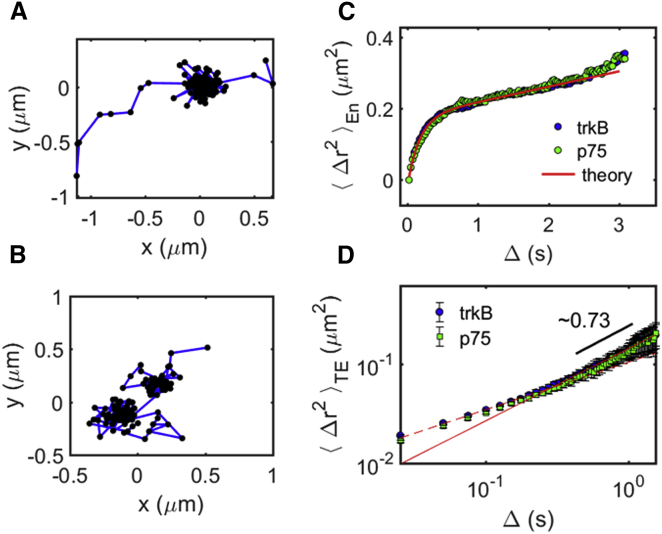
To relate the decay length of correlation in protein motion to structural features in the membrane, we analyze the single-protein stochastic motion of the proteins. Typical trajectories of receptors in the plasma membrane exhibit an alternation between two modes of motion, confined and free (Fig. 4, A and B). The transient confinement events are similarly manifested in the mean-square displacement (MSD) of both TrkB and p75 receptors (Fig. 4 C). To obtain a good estimate for the size of the confining domain, we focus on the subset of long trajectories, which are tracked for at least 3 s. The ensemble-averaged MSD, ${\langle \mathit{\Delta }{r}^2\rangle }_{En}$, of these trajectories and the time-averaged MSD, ${\langle \mathit{\Delta }{r}^2\rangle }_{TE}$, curves of both receptors agree well with each other. The MSD of a protein diffusing in a bounded domain is given by ${\langle \mathit{\Delta }{r}^2\rangle }_{En}=\langle r_D^2\rangle \left[1+A_1\exp \left(-\mathit{\Delta }/t_0\right)\right]$, where $\langle \mathit{\Delta }{r}_D^2\rangle$ is the average domain area, A₁ is a geometrical factor, t₀ is the average time it takes a protein to diffuse the length of the domain, and Δ is the lag time (38). If the bounded domain diffuses normally, the equation can be modified so that it results in the following:

$${\langle \mathit{\Delta }{r}^2\rangle }_{En}=\langle \mathit{\Delta }{r}_D^2\rangle \left[1+A_1\exp \left(-\frac{\mathit{\Delta }}{t_0}\right)\right]+4D_D\mathit{\Delta ,}$$ (2)

where D_D is the diffusion constant of the domain. Fitting Eq. 2 to Fig. 2 C, we obtain that $\langle \mathit{\Delta }{r}_D^2\rangle$ = 0.175 ± 0.003 μm², A₁ = 1.12 ± 0.03, t₀ = 0.17 ± 0.001 s, and D_D = 0.01 ± 0.001 μm²/s. Interestingly, similar domain areas were found for different cell types (38); for example, a study using superresolution imaging to measure the distribution of area size of the cortical actin networks found a wide distribution of area sizes peaked at 0.1–0.2 μm² (6). Assuming proteins undergo normal diffusion within the confined domain, we can extract the diffusion coefficient of TrkB and p75 to be $D_{p75}=D_{trkB}=\langle \mathit{\Delta }{r}_D^2\rangle /4t_0$ = 0.28 ± 0.01 μm²/s, which is 28 times larger than the diffusion constant of the confining domain. Moreover, we observe a second change in the MSD slope starting at $\mathit{\Delta }\sim 2.5$ s, which gives an estimate for the residency time in the confinement domain. The time and ensemble-averaged MSD, ${\langle \mathit{\Delta }{r}^2\rangle }_{TE}$, of both receptors is shown in Fig. 4 D. The proteins exhibit subdiffusion,$\langle \mathit{\Delta }{r}^2\rangle {}_{TE}\sim {\mathit{\Delta }}^{\alpha }$ with a power law $\alpha \sim 0.73$ for Δ > 0.05 s. We note that the time- and ensemble-averaged MSD, ${\langle \mathit{\Delta }{r}^2\rangle }_{TE}$, is qualitatively different from ${\langle \mathit{\Delta }{r}^2\rangle }_{En}$ (Fig. 4 D), indicating a nonergodic diffusion mechanism (39, 40). Similar subdiffusion behavior with similar power laws was observed previously, for example, for ion channels in Human embryonic kidney (HEK) cells (6, 41).

Figure 4.

Transient confinement in the motion of TrkB receptors in the plasma membrane of neuronal cells. The typical trajectory of the (A) TrkB receptor and (B) p75 receptor is shown. (C) Ensemble-averaged MSD of TrkB (green triangles) and p75 (purple circles) shows confinement in submicron domains for durations of several seconds. A fit of the data to Eq. 2 is shown in the red solid line. (D) Time-averaged MSD of TrkB (green triangles) and p75 (purple circles) shows a transition between a short-time power law behavior (fitted with dashed line) to a different power law behavior at long times (fitted with solid line). To see this figure in color, go online.

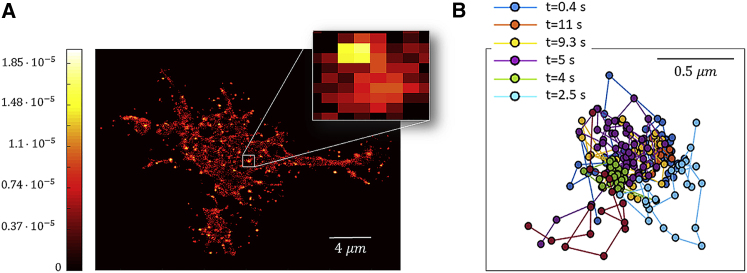
To further support the conclusion that TrkB and p75 are confined to physical domains within the membrane, we plot the two-dimensional probability distribution of finding a receptor at any location within the membrane during the entire span of an experiment, as shown in Fig. 5 A. Namely, we take into account all protein positions within a span of 15 s. Similar domains were found when studying the spatial distribution of dendritic cell-specific intercellular adhesion molecule-3-grabbing nonintegrin in Chinese hamster ovary cells (42). The analysis shows clear domains in which the occupation probability is high. A closer examination of the trajectories contributing to each domain, as shown in Fig. 5 B for the highlighted domain in Fig. 5 A, reveals that receptors entered the same domain at different times, the first entering 0.4 s after the recording started, and the last receptor entered 11 s after the recording started. We were able to observe in several cases two receptors entering the same domain or a receptor entering an occupied domain. However, our tracking algorithm is unable to follow the motion of two proteins in the same domain because their fluorescence signal overlaps most of the time in such a small domain. We note that receptors can escape a domain, as can be observed in the transient localization of the trajectories presented in Fig. 4, A and B. However, the receptors in the domain of Fig. 5 B do not seem to escape the domain. We conclude that the observed domains are actual locations within the membrane and that their lifetime is at least as long as our experiment length, which is 15 s. Further support to this observation can be found in (43), which observed stable membrane domains in neuron cells with a lifetime exceeding 30 min.

Figure 5.

Characterization of compartments in the plasma membrane from the trajectories of p75. (A) The two-dimensional probability distribution of finding a receptor at any time during the experiment is shown. Domains of higher probability are present throughout the cell; one of each is shown at higher magnification. (B) Trajectories of different receptor entering the domain in the inset of (A) are shown. Each receptor enters the domain at a different time as indicated in the figure. To see this figure in color, go online.

Discussion

The emerging picture from our combined results is that flows in the plasma membrane induced, for example, by the motion of transmembrane proteins, propagate through the membrane at intermediate distances but are arrested on a length scale equivalent to the size of these domains. Such a severe suppression of flow can result only from momentum absorption due to an immobile inclusion around which the plasma lipids cannot flow. We note that a few immobile obstacles cannot account for this flow suppression; they will affect the amplitude but not the long-range power low decay of the flow field (34).

We also find that there are physical domains in the plasma membrane. Protein receptors can diffuse into these domains and escape from them. In addition, these domains maintain their integrity for at least several seconds. The domains themselves diffuse at a low rate. It is known that domains in the plasma membrane can originate from various sources, such as lipid microdomains sensitive to cholesterol (44) and sphingomyelin concentration (45) or interactions with the underlying actin cytoskeleton (pickets and fences model) (8, 45). In addition, the motion of proteins can be affected by interactions with other biomolecules (10, 42, 46). Most probably, the motion of plasma proteins is susceptible to all these effects. It is yet unclear whether the confining domains observed here are the cause of the suppression of flow in the plasma membrane. Experiments to elucidate the source of flow suppression are currently underway.

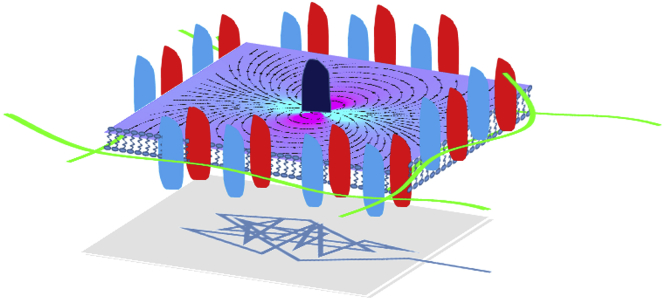
One possible interpretation of these results is that the domain boundaries are surrounded by relatively immobile obstacles (e.g., proteins anchored to underlying actin cortical mesh), which form dense enough fences to suppress lipid flow (see Fig. 6). Such an interpretation is consisted with other studies (6). Because the actin network fluctuates and changes as well as the internal section of the receptors, it is expected that these domains will diffuse and change in time on a longer timescale. This interpretation is supported by the high protein density in the plasma membrane and the many reports that implicate that the cortical actin network plays a role in restricting protein motion in the cell membrane (e.g., (6, 45, 47, 48, 49, 50, 51, 52)). Moreover, studies of the structure of the actin cortex (6, 53) show that the actin mesh size is comparable to the length scale emerging form our various measurements for domain size and flow suppression, that is, ∼0.4 μm.

Figure 6.

An optional model for flow arrest due to dense protein arrangement entangles with the underlying actin mesh. The flow field in the plasma membrane induced by protein motion decays strongly because of momentum absorption by immobile proteins. The trajectory of the tracer protein (depicted below the membrane) reflects the transient local trapping of the tracer protein. To see this figure in color, go online.

Our results and suggested interpretation provide a microscopic explanation to the surprising finding that local changes in the plasma membrane result only in a local perturbation of membrane tension (21). Combined, the observation that perturbations to membrane tension do not propagate throughout the cell have significant implication to models relying on mechanical signaling across cells.

From the vast literature concerned with the plasma membrane structure, it is clear that the factors governing its local organizations are multiple and that their combined effect is complex. How these factors affect and contribute to optimize sensing and signaling at the interface between a cell and its surrounding is still not fully understood. However, some studies hint that the passive receptor confinement in microcompartments of the plasma membrane may promote the maintenance of signaling protein complexes (52). We hypothesize that the correlated motion of proteins within these compartments may add to the integrity of such complexes without affecting proteins at larger distances.

Author Contributions

M.C. performed the experiments and part of the analysis. E.P. designed and supervised the experiments. Y.R. conceived the project, led the analysis, and wrote the manuscript.

Editor: Joseph Falke.