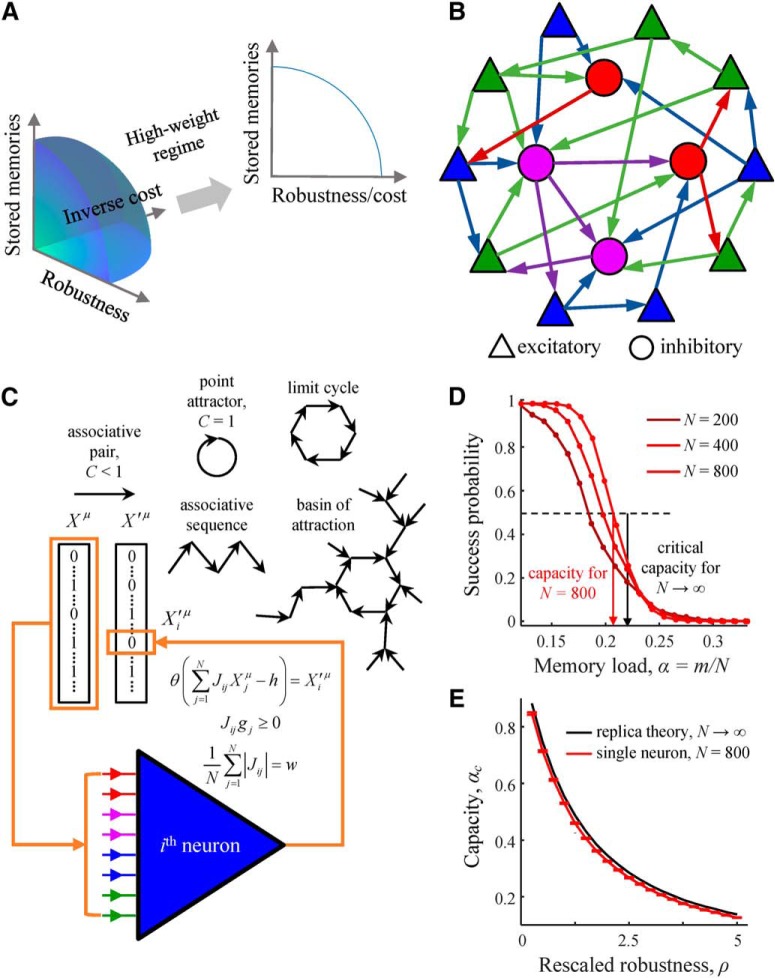
Figure 1.

Associative memory storage in recurrent networks of excitatory and inhibitory neurons. A, Associative learning in the brain is expected to be constrained by functional and metabolic considerations, such as being able to store large amounts of memories, tolerate noise during memory retrieval, and have a low cost of the underlying connectivity. In the model, these three considerations are represented with memory load, α, robustness parameter, κ, and average absolute connection weight, w. We show that, in the biologically plausible regime of high weight, results of the model depend only on α and κ/w. B, Recurrent network of various classes (color) of all-to-all potentially connected excitatory and inhibitory neurons. Arrows indicate actual (or functional) connections. C, Associative memory in the model is a connected graph of successive network states (directed edges termed associations), {X^μ→X′^μ}, in which every node has no more than one daughter node. Each neuron in the network (e.g., neuron i) must learn a set of input–output associations derived from the memory (orange boxes) by modifying the strengths of its input connections, J_ij, under the constraints on connection signs and l₁-norm. D, A neuron's ability to learn a presented set of associations decreases with the number of associations in the set, m. The memory storage capacity of the neuron, α_c (e.g., red arrow for N = 800) is defined as the fraction of associations, m/N, that can be learned with success probability of 50%. The transition from perfect learning to inability to learn the entire set of associations sharpens with increasing N and approaches the result obtained with the replica theory in the limit of N → ∞ (black arrow). Results shown correspond to associative sequences of uncorrelated network states, C = 0. Numerical results for N = 200, 400, and 800 were obtained with convex optimization (lines) and the modified perceptron learning rule (dots) (for details, see Materials and Methods). E, The capacity of a single neuron is a decreasing function of the rescaled robustness, ρ. Error bars indicate SDs calculated based on 100 networks.