Figure 2:

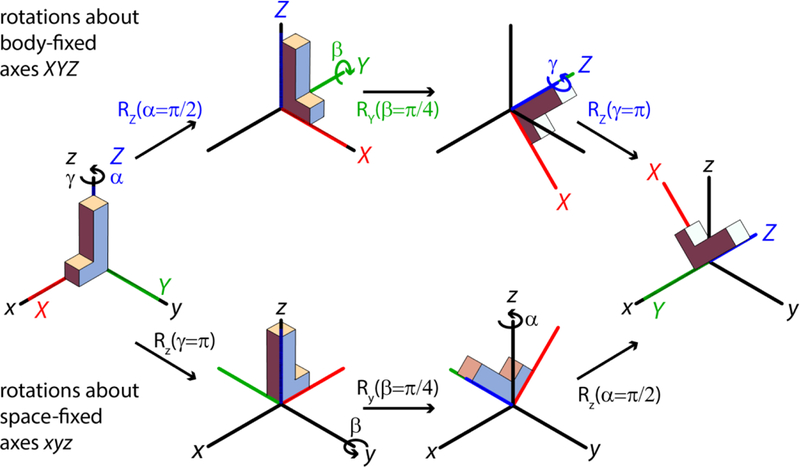
TensorView makes use of the active rotation convention to describe the rotation and orientation of an object defined by the final position of its body-fixed axes (XYZ) relative to a stationary, space-fixed reference frame (xyz). The Euler angles $\mathrm{\Omega }=\left\{\alpha ,\beta ,\gamma \right\}$ parameterize this transformation by the three successive rotations shown along the upper pathway: first an α-rotation about the object’s body-fixed Z-axis (using a right-hand rule); second, a β-rotation about its body-fixed Y-axis (in its new orientation in the space-fixed frame); third, a γ-rotation about its body-fixed Z-axis (in its final orientation). The same net transformation can be effected by three successive rotations performed entirely with respect to the space-fixed axes (bottom path): first, a γ-rotation about the z-axis; second a β-rotation about the space-fixed y axis; and finally an α-rotation about the space-fixed z axis. It is important to note the inversion in order for the α and γ rotations along the space-fixed pathway.