Zero- and high-pressure mechanisms in the complex forming reactions of OH with methanol and formaldehyde at low temperatures

Abstract

A recent Ring Polymer Molecular Dynamics study of the reactions of OH with methanol and formaldehyde, at zero pressure and below 100 K, has shown the formation of long lived complexes, with long lifetimes, longer than 100 ns for the lower temperatures studied, 20-100 K (del Mazo-Sevillano et al., 2019). These long lifetimes support the existence of multi collision events with the He buffer-gas atoms under experimental conditions, as suggested by several transition state theory studies of these reactions. In this work we study these secondary collisions, as a dynamical approach to study pressure effects on these reactions. For this purpose, the potential energy surfaces of He with H₂CO, OH, H₂O and HCO are calculated at highly accurate ab initio level. The stability of some of the complexes is studied using Path Integral Molecular dynamics techniques, determining that OH-H₂CO complexes can be formed up to 100 K or higher temperatures, while the weaker He-H₂CO complexes dissociate at approximately 50 K. The predicted IR intensity spectra shows new features which could help the identification of the OH-H₂CO complex. Finally, the He-H₂CO + OH and OH-H₂CO + He collisions are studied using quassi-classical trajectories, finding that the cross section to produce HCO + H₂O products increases with decreasing collision energy, and that it is ten times higher in the He-H₂CO + OH case.

1. Introduction

Organic molecules are among the most complex molecules observed in space, and they are called complex organic molecules¹ (COMs, while this term is generally attributed to molecules with more than 6 atoms, here we include formaldehyde among them to simplify). These molecules were first detected in the gas phase in hot cores or corinos,^2–5 at about 50 K or higher temperatures. It was then accepted that these molecules were formed on ices mantles of grains in cold cores, at 10 K, and then released to the gas phase in hot cores for dust temperatures of ≈ 100 K.⁶ Probably among the most abundant COMs, formaldehyde² and methanol³ are efficiently formed by radiation of CO-H₂ mixture ices^7,8 and by successive hydrogenation of CO on dust grains.^9–12 These reactions involving H-abstraction present barriers associated to the breaking of a bond prior to the formation of a new one, making very improbable their formation in the gas phase at low temperatures.

More recently, COMs were also detected in other environments, such as UV-shielded cold cores^13–16 at 10K, outflows^17–19 and photodissociation regions.^20,21 At 10 K in cold cores, molecules formed on ices do not thermally desorb, and several hypothesis such desorption induced by cosmic rays or by chemical desorption^22,23 are possible. Molecules with a strong electric dipole, such as methanol, are strongly bonded to the ice and do not easily desorb after UV absorption, and recent measurements have found that these molecules break releasing their photofragments to the gas phase.^24,25 A combined route is therefore possible, a synthesis on ices followed by a postprocessing in the gas phase.

This gas phase route was open recently by Heard and co-workers²⁶ who measured an extraordinary acceleration of the OH + CH₃OH reaction at temperatures below 100 K, confirmed by other experiments later.^27–30 This behavior was also found in many other reactions of OH with organic compounds involving alcohol, ether, and aldehyde groups^31–35 when studied using laval expansion experiments. In these experiments, the measured reaction rate showed a non-Arrhenius behavior, with V-shaped form versus temperature, with a minimum at about 200-300 K for all of them, independently of the height of the reaction barrier. The increase of the reaction rate constant below 100 K was originally explained by the formation of collision complexes between reactants followed by tunneling through the reaction barrier.^26,35 The formation of the complex is very reasonable because all the organic molecules studied have strong dipole moments giving rise to important long range interactions with OH, and a relatively deep well associated to the COM-OH complex. However, some controversy, associated to the tunneling, persists as explained below.³⁶

Several transition state theory (TST) studies have been performed,^30,36–38 especially on the OH + CH₃OH reaction, concluding that the tunneling is too low. In all these studies, the rise of the reaction rate constant is explained by the pressure. First, Siebrand and co-workers³⁶ proposed a model based on the formation of methanol dimer in the expansion. However, a high density of dimers is necessary to reproduce the experimental data, which seems to be too high according to the experimental conditions.³⁹ Later, Gao and co-workers³⁷ made a systematic study of this reaction using the competitive canonical unified statistical (CCUS) model in the low and high pressure limits, showing that at low temperatures the rate constant becomes pressure dependent. In this model,³⁷ the stabilization of the reaction complex in the low pressure limit (LPL) was not included and only at high pressure the complex is formed over a wide energy interval thus allowing tunneling. More recently, the formation of the complex was considered within the low pressure limit in a TST formalism,³⁰ but it was necessary to consider also the high pressure limit (HPL) to get a good agreement with the experimental data below 100K, fitting some free parameters of the models. Also, the OH + CH₃OH reaction was recently studied using a two-dimensional master-equation/semi-classical TST/variational Rice-Ramsperger-Kassel-Marcus approach, and it was found that below 250 K the reaction rate constant depends strongly on pressure.

The pressure dependence at low temperature is nearly impossible to eliminate from the CRESU experiments (French acronym of the uniform gas expansion technique) due to the necessity of using a buffer gas, usually helium, in the laval expansion.^26–30 However, in the interstellar medium the density is very low and the LPL rate constant is needed in astrophysical models. It is therefore of paramount importance to combine experimental and theoretical studies to extract the LPL reaction cross section. For doing so, dynamical studies without ad hoc parameters are expected to be of great help. At this regards, we have recently developed the full dimensional potential energy surface (PES) for two reactions, H₂CO^33,40 and CH₃OH⁴¹ with OH. Quasi-classical trajectory (QCT) calculations performed on these potentials showed the mentioned increase of the reaction rate constant below 100 K, originated by a complex forming mechanism in the two reactions. Thus, for H₂CO + OH, the QCT rate constants are in rather good agreement with the experimental data,³³ while for CH₃OH + OH,⁴¹ with higher barriers, the calculated rate constant remains nearly constant below 100 K, in qualitative agreement with the previous TST studies. However, quantum effects are important at low temperatures, such as tunneling and zero-point energy (ZPE). In order to include these effects, very recently Ring Polymer Molecular Dynamics (RPMD) calculations were performed on the reactions of OH with formaldehyde and methanol⁴² showing the formation of extremely long lived collision complexes, with lifetimes longer than 100 ns, and a very large capture rate. This finding opens the possibility that the zero-pressure reaction cross section of these reactions also increases below 100 K, and it is important to determine as accurately as possible such effects.

In this work, we present a preliminary study of the pressure effect by determining the effects of the interaction of the reactants with helium on the H₂CO + OH reaction dynamics. The manuscript is distributed as follows. In section II the method used for the analytical representation of the full dimensional PESs is briefly presented and extended to the case of including the interactions with He. In section III, previous dynamical calculations, QCT and RPMD, are summarized and discussed for the title reactions, to show the results in the zero-pressure limit. In section IV, preliminary QCT calculations are presented for the H₂CO + OH system in the presence of one Helium atom as a prototype to study the pressure effect dynamically. Finally, section V is devoted to extract some conclusions.

2. Potential energy surfaces

The two reactions studied here present exothermic H-abstraction mechanism with barriers,

$$H_{2}CO+OH\to HCO+H_{2}O$$ (1)

and

$$\begin{array}{l}C{H}_{3}OH+OH\to C{H}_{3}O+H_{2}O{R}_1\\ C{H}_{3}OH+OH\to C{H}_{2}OH+H_{2}O{R}_2.\end{array}$$ (2)

The study of reaction dynamics at low temperature requires the use of highly accurate ab initio methods to reproduce long range interactions, reaction barriers, etc. Also, long propagation times are needed, involving many integration steps and many evaluations of the electronic energy. Therefore, it is required the use of hyperdimensional potential energy surfaces, which are generally developed as analytic fits of ab initio points.

Recently, analytical fits of the full dimensional PES have been developed for the two title reactions,^40,41 which were partitioned in two terms, H^diab + H^MB. H^diab is a diabatic matrix in which each diagonal element (channel) corresponds to a single rearrangement channel. For H₂CO + OH this matrix is of dimension 3× 3 (there are two equivalent products channel in Eq. (1)), and for CH₃OH + OH the dimension is 5 (there are 3 equivalent channels in Eq. (2.b)). This terms includes the long range dipole-dipole interaction between reactants, crucial in the low temperature dynamics. The second term, H^MB, is the many-body term described by permutationally invariant polynomials following the method of Aguado et al.^43,44 For the two reactions studied, more than 2 × 10⁵ CCSD(T)-F12a ab initio points have been used to fit this term, as described previously for H₂CO + OH⁴⁰ and CH₃OH +OH,⁴¹ respectively. The details of the corresponding PESs are summarized in Fig. 1.

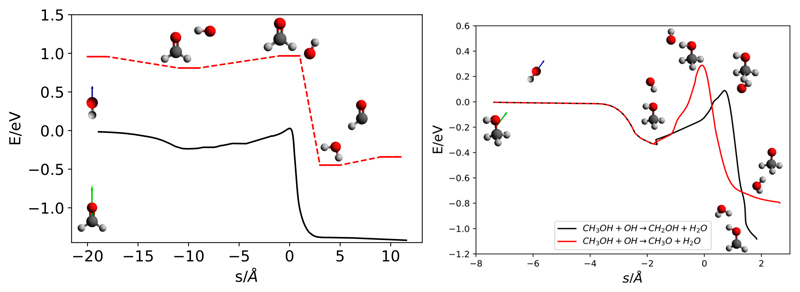
Figure 1.

Minimum energy paths for H₂CO +OH (left) and CH₃OH+OH (right) reactions, summarizing the main features of the PESs. For the CH₃OH + OH case, black and red lines correspond to CH₂OH + H₂O and CH₃O + H₂O products, respectively. In dashed lines, a common path for both reactions from the asymptotic reactant geometries to the reactive complex is presented.

In both cases, there is a dipole-dipole long range interaction between OH and the COM that determines the capture, and a well of ≈ 0.3 eV, corresponding to the collision complex COM⋯ OH. The electric dipole in H₂CO is parallel to the CO bond while in CH₃OH it goes approximately from the center of C-O bond to the opposite side of H in the OH group, as indicated schematically in Fig. 1.

The lowest barrier is that of H₂CO +OH reaction (of ≈ 27 meV without ZPE), while for methanol the barriers are higher, of 89 and 289 meV for the R₂ and R₁ mechanisms in Eq. 2, corresponding to the abstraction of one H from the CH₃ or OH group. For methanol, the minimum energy path (MEP) shows a common reactive complex for both reactions, respectively. For the abstraction of an H via R1 reaction, the oxygen of the OH radical has to approach the hydrogen of the alcohol group, being that a movement of shorter amplitude than via R2. This explains why QCT calculations predict the branching ratio CH₃O/CH₂OH to be approximately 3 below 100 K.

The interaction of He is considered additive since He is chemically inert. In the case of reaction 1, it is built by adding the He-OH and He-H₂CO interactions to their corresponding matrix diagonal elements in H^diab term briefly described above. Each interaction term is build individually keeping the molecule frozen in its equilibrium geometry and performing high-level ab initio calculations for multiple positions of He around it, as detailed below.

2.1. Interactions with He atoms

For consistency, we have used the same R/CCSD(T)-F12a method with the cc-PVQZ-F12 basis set, both implemented in the MOLPRO package,⁴⁵ as in the previous papers.^40,41 Energies for each PES have been calculated for 19 radial points between 2 and 10 Å(spaced more densely near the minima) along 9 cuts between 0° and 180°, with the polar-coordinate origin at the center of mass of the molecule (H₂CO, HCO, H₂O or OH). Then the values have been interpolated with cubic splines radially and with Legendre polynomials angularly. The radial cuts have been extrapolated beyond 10 Å with a R⁻⁶ tail. For He-H₂CO, coplanar and several nonplanar (with He located respectively in and out of the molecule plane) 2D sub-PES have been produced. The obtained energy variation with the dihedral angle ϕ= HeOCH between 0° (planar) and 90° (perpendicular) geometry has been closely approximated with a switching function sin² ϕ via V = V₀ + (V₉₀–V₀) sin² ϕ. A similar approach has been used for the He-H₂O and He-HCO, the latter featuring two planar half-PESs, with and without the H atom. The PES are illustrated in Figs. 2 and 3.

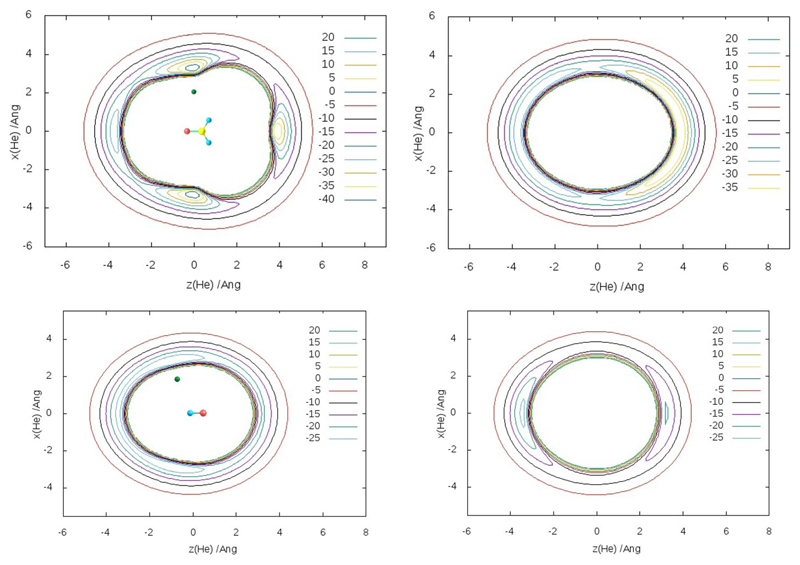
Figure 2.

Contour maps (in cm⁻¹) of the calculated He-H₂CO PES (top), for planar and perpendicular configurations, and He-OH A´ and A´´ PES (bottom).

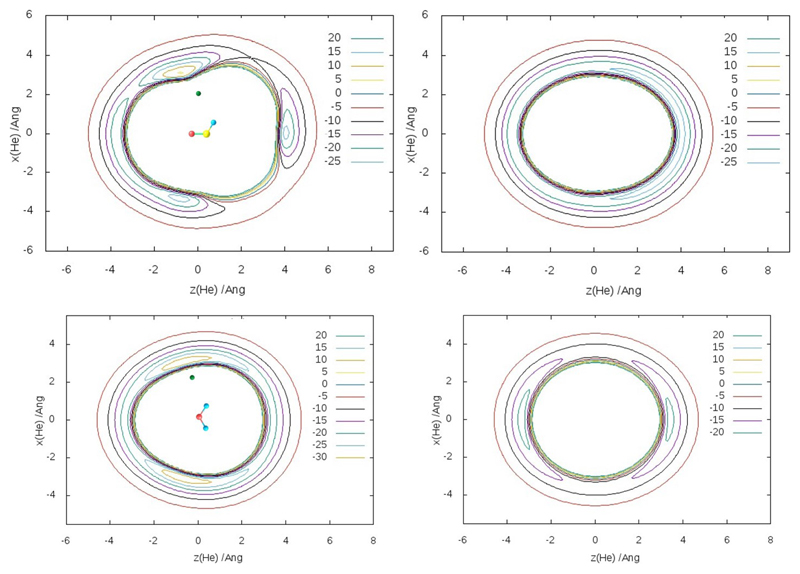
Figure 3.

Contour maps (in cm⁻¹) of the calculated He-HCO (top) and He-H₂O planar and perpendicular (left and right) PES.

The He-H₂CO PES has four minima of energy, with He axially at each end of the molecule (more stably between the H atoms of H₂CO) and at the symmetric co-planar positions near-perpendicular to the C-O axis, which are slightly still more stable. This is consistent with the earlier work.⁴⁶ The relative stabilities of these conformers could be interpreted by the combination of van der Waals interactions and those with the partial charges on atoms. In particular, the deeper collinear minimum in the H side relative to that in the O side could be due to smaller H’s allowing for a closer approach of He and stronger interactions with their charges. The deepest minimum in the near-T-shaped conformation could benefit from the stronger He-O as compared to He-H van der Waals interaction. In addition, the reduction of the He-H interaction might be responsible for destabilization in the nonplanar geometries. Alternative interpretations are based on the relative repulsion of He by the electron density of the CO component in different geometries⁴⁶.

For He-OH, both A´ and A´´ PESs are shallower and flatter angularly, with the stable energy minimum for A´ corresponding to He attached sideways and shifted to (smaller) H. Accordingly, the lower-energy A´-state PES has been employed further in the present work.

The removal of H from H₂CO, making HCO, destabilizes the interaction with He, especially for the coplanar minimum of energy on the “H-lacking” side. This minimum becomes much more delocalized, shallower towards the O end, and thus destroys the axial minimum there via removing the barrier separating it. Similar evolutions apply to the He-H₂O interaction when the system is transformed to He-OH. In addition to becoming shallower, more so towards the H end, the energy minimum is fully delocalized around the O-H axis, thus transforming to a ring.

The He-H₂O PES features only symmetric coplanar wells on the sides of the molecule, and, unlike the He-H₂CO, no axial minima, even in the hollow between the H atoms. This could be related to the repulsion of He from the electron density of the doubly-occupied p-orbital of oxygen perpendicular to the plane of H₂O (composing its HOMO orbital). Upon “insertion” of C in the middle of H₂O to make H₂CO, this density is moved axially inwards from both ends of the molecule, more so on the H side.

The above PESs parameters are listed in Table 1 and compared with the previous values from literature.

Table 1. Calculated equilibrium parameters of the He complexes.

System	De (cm−1)	Re (Å)	Θe
He-H2CO	44.0	3.27	91°
Ref.46	59.4	3.08	97°
He-OH	29.8	2.98	108°
Ref47	30.0	3.01	111°
Ref48	29.8	3.01	111°
Ref.49	29.8	3.02	113°
He-HCO	35.3	3.21	104°
He-H2O	33.4	3.13	104°
Ref.50	34.1	3.14	104°
Refs.51,52	34.9	3.12; 3.13	102°; 105°
Ref.53	30.4	3.19	101°

Our He-H₂CO PES exhibits a somewhat lower binding than the previous basis-set extrapolated CCSD(T) one⁴⁶. This could be related to using (smaller) aug-cc-PVXZ (X=D,T) basis sets for the extrapolation of that PES. They have also calculated a well depth of about 50 cm⁻¹ for the aug-cc-PVQZ basis set, matched by our value more closely. A further support comes from comparison of the PES parameters of similar, same-core He-CO. The corresponding previous results⁴⁶ are De = 23.4 cm⁻¹ at Re = 3.46 Å and θ_e = 63.2°, while the extrapolation with larger aug-cc-PVXZ (X=T,Q) basis sets in later work⁵⁴ gives 22.0 cm⁻¹ at 3.40 Åand 70.8°, matched better by our 21 cm⁻¹ at 3.40 Å and 69°.

For He-OH, our PES appears to be in a good agreement with the recent PESs also obtained at the RCCSD(T) level and using aug-cc-PVTZ+spdfg-bond-functions,⁴⁷ aug-cc-PV5Z+spdfg-bond-functions⁴⁸ or basis-set-extrapolated from aug-cc-PVXZ (X=Q,5,6).⁴⁹ The differences do not exceed 1% in both D_e and R_e or 5% in θ_e.

The deepest well for HCO (in the coplanar conformation) is about 20% (10 cm⁻¹) shallower than for H₂CO and shifts slightly nearer to the molecule as a result of the H atom removal. Such variations increase for the axial energy minimum on the H side and further for the shallowest coplanar minimum on the “H-lacking” side (up to 20 cm⁻¹ in D_e). The energy gap between the axial (H-side) and deepest minima thus increases from about 5 cm⁻¹ in H₂CO to about 10 cm⁻¹ in HCO. It is worth noting that upon removal from HCO of the remaining H to make CO, the interaction with He is consistently destabilazed further. In particular, the coplanar well becomes symmetrically shallower on both sides while the axial well is levelled out.

For He-H₂O, our PES parameters are close to those from previous works at the CCSD(T)/aug-cc-PVQZ+spdfg-bond-functions⁵⁰ and SAPT^51,52 levels within 1 cm⁻¹ and 0.01 Å. Somewhat larger differences, up to 10% in D_e, are found from the CCSD(T)/aug-cc-PVTZ data⁵³ with a smaller basis set.

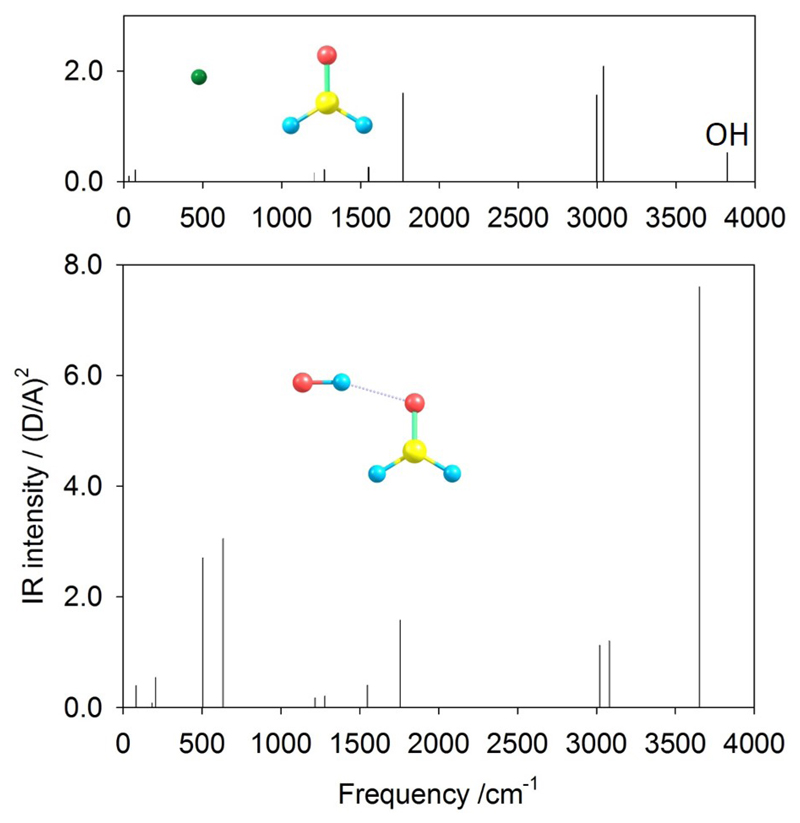
The weak He-H₂CO interaction is predicted to be represented by a couple of weak IR spectral lines of the complex in the low-frequency range of under 100 cm⁻¹ (Fig. 4). While the main set of lines, above 1000 cm⁻¹ and up to an order of magnitude more intense, is essentially preserved from the isolated H₂CO, the variations do not exceed 3 cm⁻¹ shift in the line positions. This is different for the (more strongly) hydrogen-bonded OH-H₂CO complex. The three major lines of H₂CO, one near 1800 and two 3000 cm⁻¹ are affected relatively weakly, via a 10 cm⁻¹ red-shift or 30-40 cm⁻¹ blue-shift, respectively, and the latter pair is almost halved in intensity. The formation of the complex is clearly manifested by the three new bright lines near 500-600 and 3600 cm⁻¹, all dominated by OH vibrations. The latter, most intense line corresponds to the O-H stretch, red-shifted by about 170 cm⁻¹ and brightened by more than an order of magnitude relative to the isolated OH. This is likely due to H atom shuttling between two O atoms, accompanied by considerable dipole-moment alterations. The above shift is nearly identical to 175 cm⁻¹, predicted⁵⁵ at the same level of theory for the OH-CH₃OH complex (while their corresponding experimental shift is 50 cm⁻¹ smaller). The similarity of the shifts suggests similar influences on OH of CH₂O and CH₃OH, which, however, have rather different dipole moments calculated as 2.39 and 1.67 D, respectively. A likely rationalization here is a less favorable (interaction-wise) alignment of the molecular-component dipoles in OH-CH₂O relative to OH-CH₃OH. This is consistent with the smaller total dipole of the former compared to the latter, predicted to be, respectively, about 3.56 and 4.03 D. The other two lines originate from the OH-bending (H-wagging) vibrations in and (lower-frequency) perpendicular to the H₂CO plane. These are less than half as bright as the OH-stretching mode but of about double intensity compared to the H₂CO-related lines. These two lines are beyond the range investigated in the earlier work.⁵⁵

Figure 4.

Calculated IR intensity spectra of He-H₂CO (top) and OH-H₂CO. In the top panel, the OH line is added for clarity.

By comparison, the predicted spectrum of the (H₂CO)₂ dimer is dominated by the lines of a monomer. Only a couple of lines, in the 100-200 cm⁻¹ range, with an intensity half of the monomer are new and can be considered as a representative of the dimer.

3. Dynamics of the gas phase reaction: zero pressure

The reaction dynamics was studied using a QCT method for H₂CO+OH^33,40 and CH₃OH +OH.⁴¹ For the H₂CO + OH reaction, QCT results mimic rather satisfactorily the experimental data, showing an increase below 300 K as the experimental results. The reaction barrier in this case is only of 27 meV (≈ 232 K), which is reduced to only ≈ 10 meV when ZPE is taken into account. This small energy can be easily transfered due to anharmonic effects from the orthogonal vibrational modes, and this could explain why QCT works so well.

In contrast, the QCT obtained for the CH₃OH +OH reaction do not show an increase as important as the experimental results below 200 K. This disagreement was attributed to quantum effects, such as tunneling and ZPE, important at low temperature.

Rigorous quantum methods are not feasible due to the high number of dimensions involved in the reaction dynamics. RPMD method, which has already shown itself as a reliable alternative^56–60 was used recently to study the reactions of OH with formaldehyde and methanol.⁴² RPMD is a semiclassical formalism based on Path Integral Molecular Dynamics (PIMD) which includes quantum effects as ZPE⁶¹ and tunneling,⁶² and it has been demonstrated to be a very powerful technique to describe low-temperature reaction dynamics.^60?

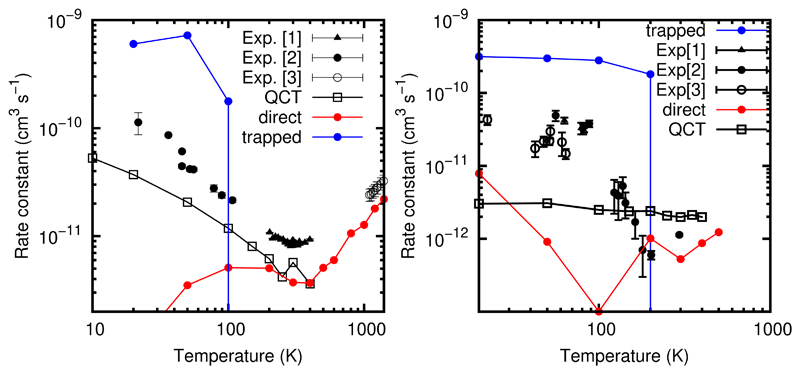
In Ref.,⁴² the RPMD description of the two reactions under study followed two very different mechanisms, one direct at T> 200 K and a second indirect at T<200 K, as it is shown in Fig. 5. The direct mechanism corresponds to a H-abstraction mechanism. This process is fast, and all reactive RPMD trajectories which finish in less than few ps were considered to be direct. Note that the time required for the approach of the two reactants (capture time) is rather long because of the low temperatures considered, becoming an important fraction of the whole time of each trajectory.

Figure 5.

Direct reaction and direct rate constants obtained with the RPMD method for H₂CO + OH (left panel) and CH₃OH reactions (right panels). The QCT reaction rate constants are taken from Refs.,^40,41 respectively. The [1,2,3] experimental results are Refs.^33,63,64 for H₂CO + OH reaction and^26,27,29 for CH₃OH+OH reactions, respectively.

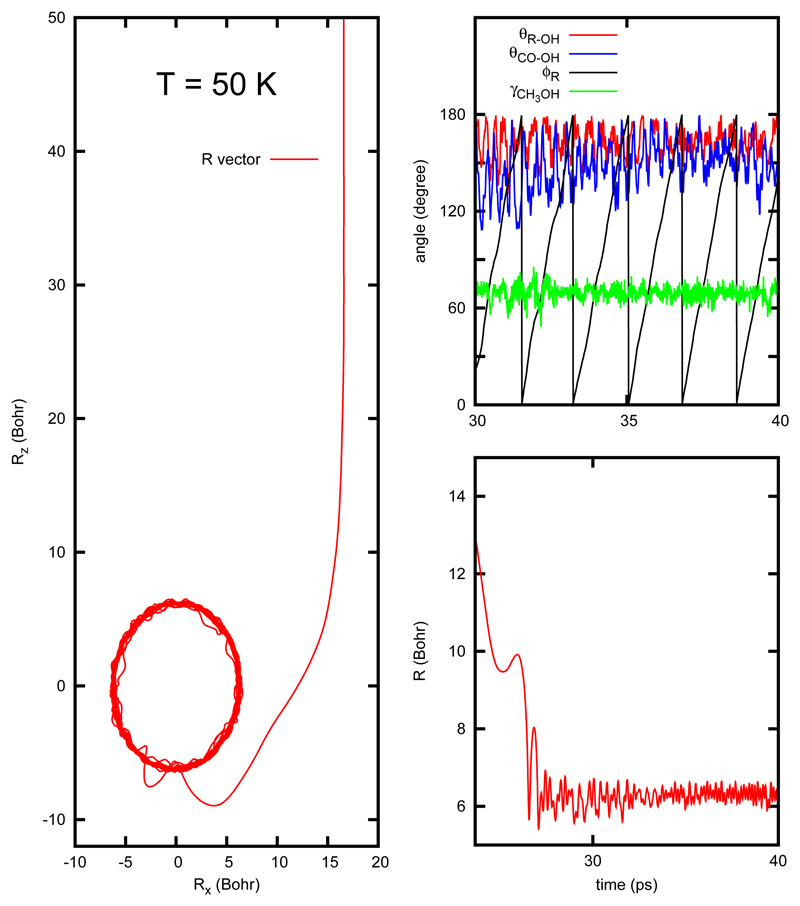
The indirect mechanism corresponds to trapping, and a typical RPMD trajectory of this type obtained for the CH₃OH +OH reaction at 50 K is shown in Fig. 6. At such low temperature, the capture increases because of the strong long range dipole-dipole interaction. This implies that the maximum impact parameter increases significantly, and the dipole-dipole interaction is able to deviate the trajectory until the two reactants start rotating around each other, as shown in the left panel of Fig. 6. Along this rotation, the vector R is turning along a circular orbit as shown by the azimuthal angle ϕ_R in the top-right panel of the figure. However, the relative orientation of the two reactants is kept fixed, as well as the torsional angle γ_CH3OH, shown in the same figure, in a configuration very close to the minimum of the CH₃OH⋯ OH well. This implies that the two reactants have a high rotational angular momentum, and also the end-over-end angular momentum is very high. On the contrary, the internal vibrations of the reactants and the van der Waals stretching between them (shown in the lower panel of Fig. 6) keep restricted to a much narrower radial interval, demonstrating that these modes are not very excited in the complexes. Similar results were recently reported for the H₂CO+OH reaction described above,⁴² indicating that this is a rather general result, and that these kind of resonances have a very long lifetime, what gives rise to the trapping.

Figure 6.

Evolution of the vector R, between the centers-of-mass of reactants using the centroid for a RPMD trajectory at 50 K (left panels) for the CH₃OH +OH reaction. In the upper right panels, the evolution of the angles between R and r_OH and r_CO and r_OH are displayed for a short period of time. The angle ϕ_R = arctan (R_x/R_z) represents the end-over-end rotation of OH with respect to CH₃OH. The angle γ is the torsion angle of CH₃OH corresponding to one of the H atoms with respect to the COH group.

At this point we differentiate between capture and trapping. Capture is the first part of the trajectory in which the strong dipole-dipole interaction forces the two fragments to approach each other, as in the first 25 ps of the RPMD trajectory of Fig. 6. The capture is responsible for the orbital motion of reactants with respect to each other. When running classical trajectories, this kind of orbits is also obtained, but the difference is that they only live for a few ps. However, when quantum effects are considered, like in the RPMD trajectories, the number of open channels of the reactants is very small, and the collision complex lifetime increases a lot. These quantum effects give rise to the trapping of the collision complexes for very long times, which we estimate here to be longer than 0.1 μs.

These long complex lifetimes become closer to the time scale of tunneling through barriers, making possible that the reaction may take place. In fact, the collision complex can dissociate back to reactants, the redissociation process, or tunnel to form products. Therefore, complex forming reactive rate constant is given by

$$k_{CF}\left(T\right)=k_{trap}\left(T\right)\frac{k_{tunnel}\left(T\right)}{k_{tunnel}\left(T\right)+k_{rediss}\left(T\right)},$$ (3)

where k_trap(T) is shown in Fig. 5 in blue. In this expression, k_tunnel(T) and k_rediss(T) are the tunneling and redissociation rate constants, respectively.

In the case of H₂CO + OH reaction, the k_tunnel(T)/[k_tunnel(T) + k_rediss(T)] branching ratio was taken from the QCT calculations, leading to results rather similar to the experimental values.⁴² The differences were attributed to inaccuracies of the PES specially at high temperatures, and some work is now-a-days in progress to solve this problem. In addition, pressure effects may also play a role, but only at low temperature, as discussed below.

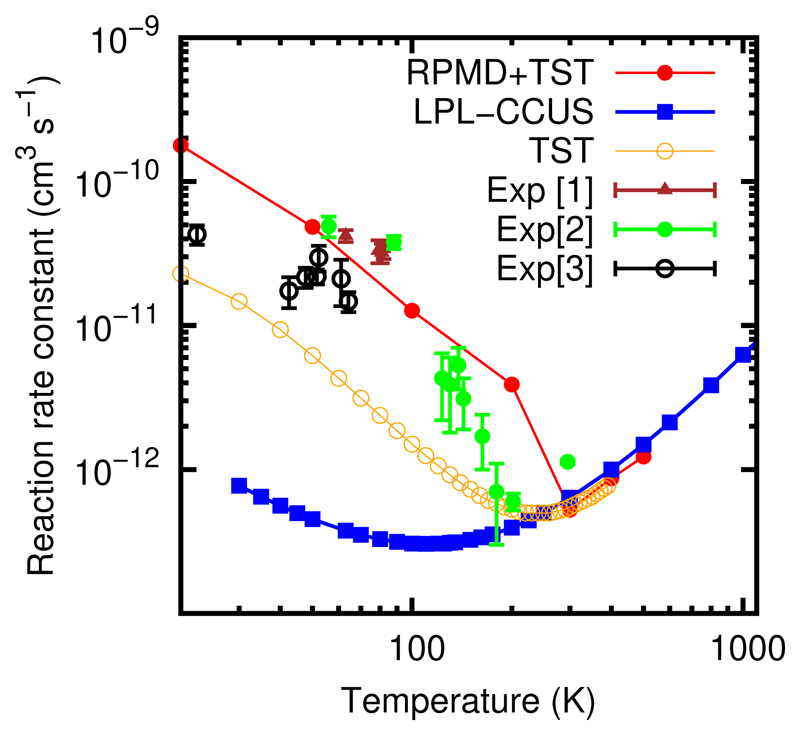
In the case of CH₃OH + OH, the k_tunnel(T)/[k_tunnel(T) + k_rediss(T)] ratio was obtained from the low pressure TST studies performed by Ocaña et al.,³⁰ following the method explained before.⁴² The total reaction rate constant is the sum of the direct and complex forming contribution. In this study, we have added the results obtained for 20 K for the CH₃OH + OH reaction, which were not included before, and that are shown in Fig. 7. The RPMD results combined with the TST ratio are always larger than the TST results obtained in the low pressure limit by Ocaña et al.³⁰ and Gao et al.,³⁷ showing that the trapping is more efficient when the system is treated in full dimensions and when the quantum effects are taken into account. The agreement with the experimental data is excellent, except for 20 K, where the RPMD is slightly higher than the experimental result due essentially to the increase of the k_tunnel(T)/[k_tunnel(T) + k_rediss(T)] ratio. This good agreement for the CH₃OH +OH reaction may be taken in part as fortuitous since there are aspects to be improved in the simulations, namely the potential energy surface and the calculation of the k_tunnel(T)/[k_tunnel(T)+ k_rediss(T)] ratio which should also include the multidimensional character. Nevertheless, these results indicate that the experimental results reported below 100 K^26,27,29,30 can also be explained by assuming the zero-pressure limit, and not only by assuming pressure effects as used in TST-like formalisms so far.^30,37,38 It is therefore of paramount importance to determine the real effect of pressure on the experimental reaction rate constant not only by fitting their role to the experimental data, but by performing dynamical calculations.

Figure 7.

Total reaction rate constant obtained in the zero-pressure limit for the CH₃OH + OH reaction with the RPMD calculations. The results were obtained in Ref.⁴² except that obtained for 20K, added in this work. The [1,2,3,4] experimental results are from Refs.,^26,27,29,30 respectively. LPL–CCUS are taking from Ref.³⁷ TST referes to the TST (RRKM) results obtained in the LPL in Ref.³⁰

The fact that pressure may play a role in the experimental values reported is justified by the long lifetimes of the collision complexes, since at the densities of the laval expansion at low temperatures the time between collisions with the buffer gas is estimated to be of the order of 1-100 μs (E. Jiménez, private communication). Thus, long-lived collision complex can collide with the buffer gas used in CRESU experiments. This result reconciliates with the high pressure TST models to explain the rise of the reaction rate constant at low temperatures and, at the same time, is taken as an indication that the reaction rate constant at zero pressure also increases at low temperatures. Such collisions induce changes which are responsible for the pressure effects, and deserve a further study, which is presented below.

4. Collisions with He: high pressure effects

In the laval expansions used in the CRESU experiments there must be a buffer gas. This buffer gas is frequently Helium, and it is more than 3 orders of magnitude more abundant than any of the two reactants, the COM and the OH. Also, in general, the density of the COM is higher than that of OH, because this radical is produced by photolysis (E. Jiménez, private communication). At low temperatures, complexes like He⋯ H₂CO, He⋯ OH, H₂CO ⋯ H₂CO and OH ⋯ H₂CO will be formed in this order if only relative density is considered.

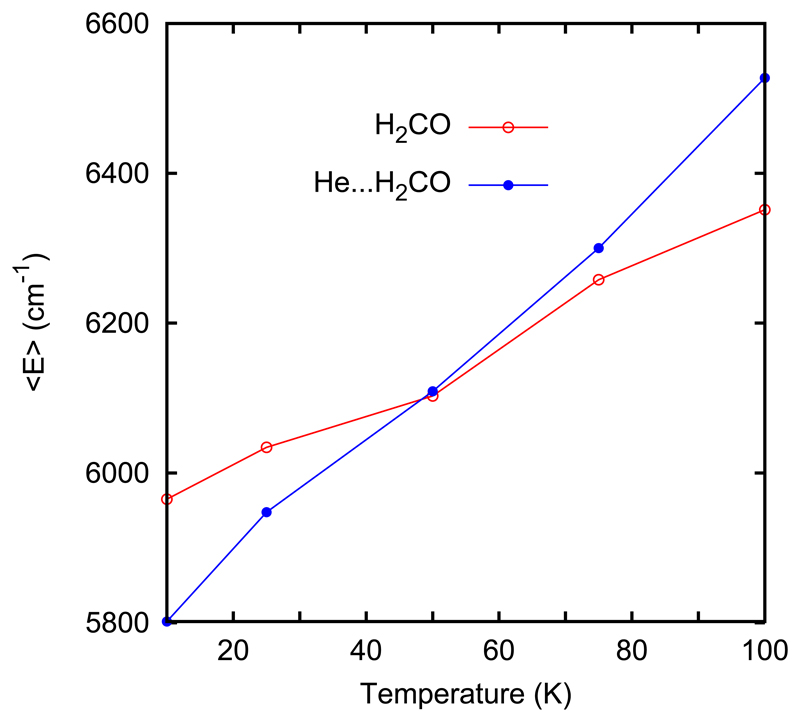
However, stability will also play a role. For example, the RPMD study discussed above allows us to say that the OH ⋯ H₂CO complexes are formed and live long enough between 100 and 200 K. Here we will also like to study at what temperature He⋯ H₂CO complexes are no longer formed, or live short time. For doing so, we have performed PIMD calculations with no contraints for H₂CO and He⋯ H₂CO at several temperatures. 10⁶ integrations were done in each PIMD propagation, and the average free energy is calculated,⁶⁵ see Fig. 8. The zero of energy is taken at the bottom of the H₂CO well, isolated, and the He ⋯ H₂CO van der Waals interaction is weak and negative. Therefore, at low temperature < E >_He–H2CO is below that of bare H₂CO, < E >_H2CO. As temperature increases, more and more levels are populated, and soon the weak He ⋯ H₂CO interaction is broken, i.e. the continuum states of He +H₂CO are populated which have a positive energy. As a consequence, the order of the mean energy is reversed at 100 K, and the crossing point is at ≈ 50 K. In addition, the distribution of the distance between He and the center of mass of H₂CO increases a lot for T > 50 K, what is also taken as an indication that at those temperatures the He⋯ H₂CO complex dissociates fast. We take T = 50 K as a rough estimate of the temperature at which the He⋯ H₂CO dissociates fast. This temperature for the OH⋯ H₂CO complex is higher, above 100 K. We can then separate the contributions of these two complexes in two temperature ranges: while both are important below 50 K, between 50 and 150 K only the OH⋯ H₂CO collision complexes are playing a significant role.

Figure 8.

Mean energy of H₂CO and He⋯ H₂CO as a function of temperature

In order to study how energy is transferred in collisions of any of these complexes with other species in the beam, we present here the QCT results for the H₂CO ⋯ He + OH and H₂CO ⋯ OH + He collisions, to determine which are the dominant fragmentation channels. In the two cases, the initial conditions are determined by the adiabatic switching method,^66–69 using the normal modes calculated at the bottom of the corresponding potential well, as described previously.^33,40 The interaction of He with H₂CO is so weak and anharmonic that the system fragments when using all the vibrational modes. To avoid fragmentation, in this case the three modes associated with the van der Waals interaction were neglected.

It is important to note the long range interactions for the two cases. For OH + He-H₂CO collisions, the leading term is the strong dipole-dipole interaction, and for this reason the initial distance between reactants is set to 120 bohr, as in the OH + H₂CO with no He. Accordingly, the maximum impact parameter is rather large and is calculated with a capture model⁷⁰ depending on the collision energy. In the He + OH-H₂CO case, however, the dispersion long range interaction is much weaker, and the initial distance was set to 50 bohr, and the maximum impact parameter of 20 bohr. The calculations have been performed at fixed collision energies and 10⁴ trajectories were run in each case.

For OH + He-H₂CO collisions, the examinated fragmentation channels are

$$\begin{array}{ll}{H}_{2}CO\cdots He+OH\to H_{2}CO\cdots He+OH\hfill & \hfill \text{Inelastic}\\ \to H_{2}CO+He+OH\hfill & \hfill \text{Complex}\text{dissociation}\\ \to H_{2}CO+He\cdots OH\hfill & \hfill \text{He}–\text{exchange}\\ \to H_{2}CO\cdots OH+He\hfill & \hfill \text{Complex}\text{forming}\\ \to HCO+He+H_{2}O\hfill & \hfill \text{Reaction.}\end{array}$$ (4)

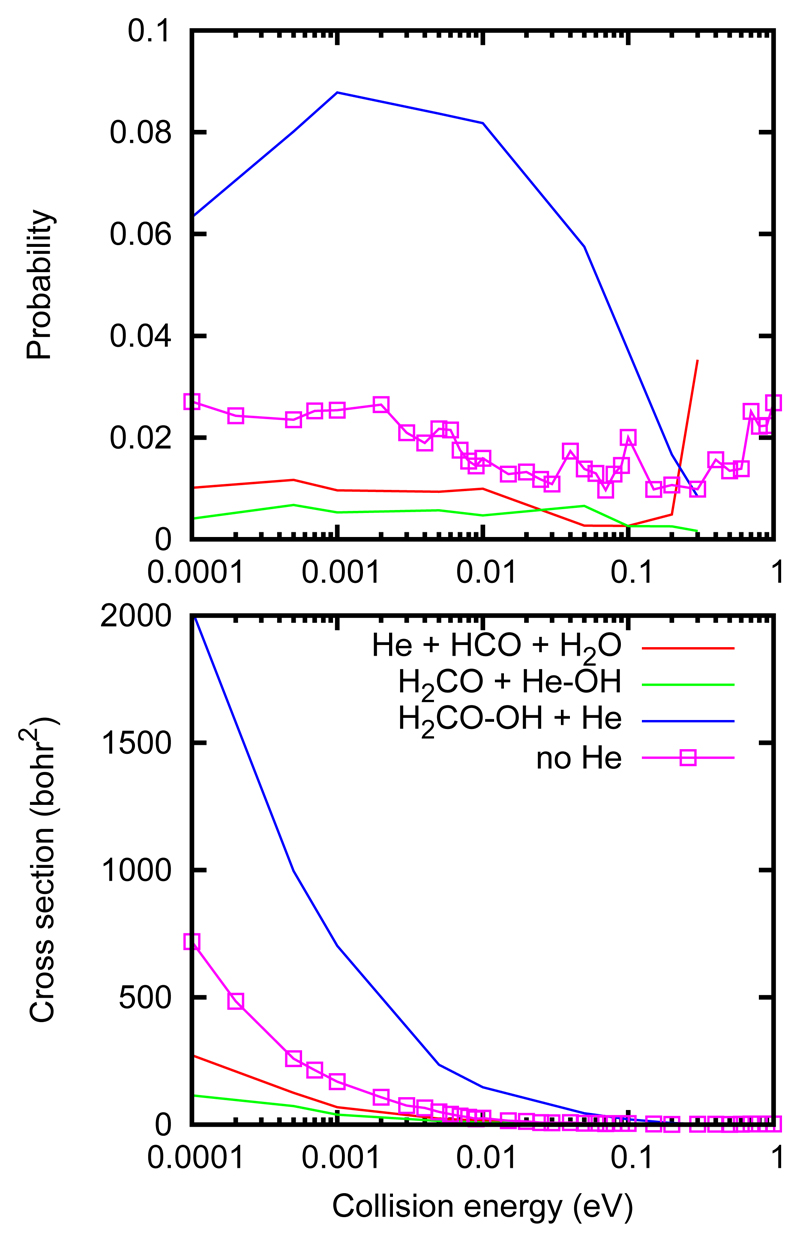
Complex dissociation and He-exchange are new rearrangement channels, but are directly linked to the reaction though they will reduce the probabilities of other channels. The two channels more relevant for the reactivity are the last two, the complex forming and the reaction. The cross sections and probabilities for each process are shown in Fig. 9, and compared with the QCT calculations performed for the H₂CO + OH reaction with no He.

Figure 9.

QCT cross sections (bottom panel) and probability (top panel) for the processes of Eq. 4 in the He⋯ H₂CO + OH collisions.

It can be seen that the reaction channel, in red, is reduced with respect to the case without He. The He exchange between H₂CO and OH is also possible but is always smaller. The dominant channel below 0.1 eV of collision energy is the complex forming channel, in blue, whose cross section increases with decreasing collision energy. This channel indicates a very efficient energy exchange between OH and He.

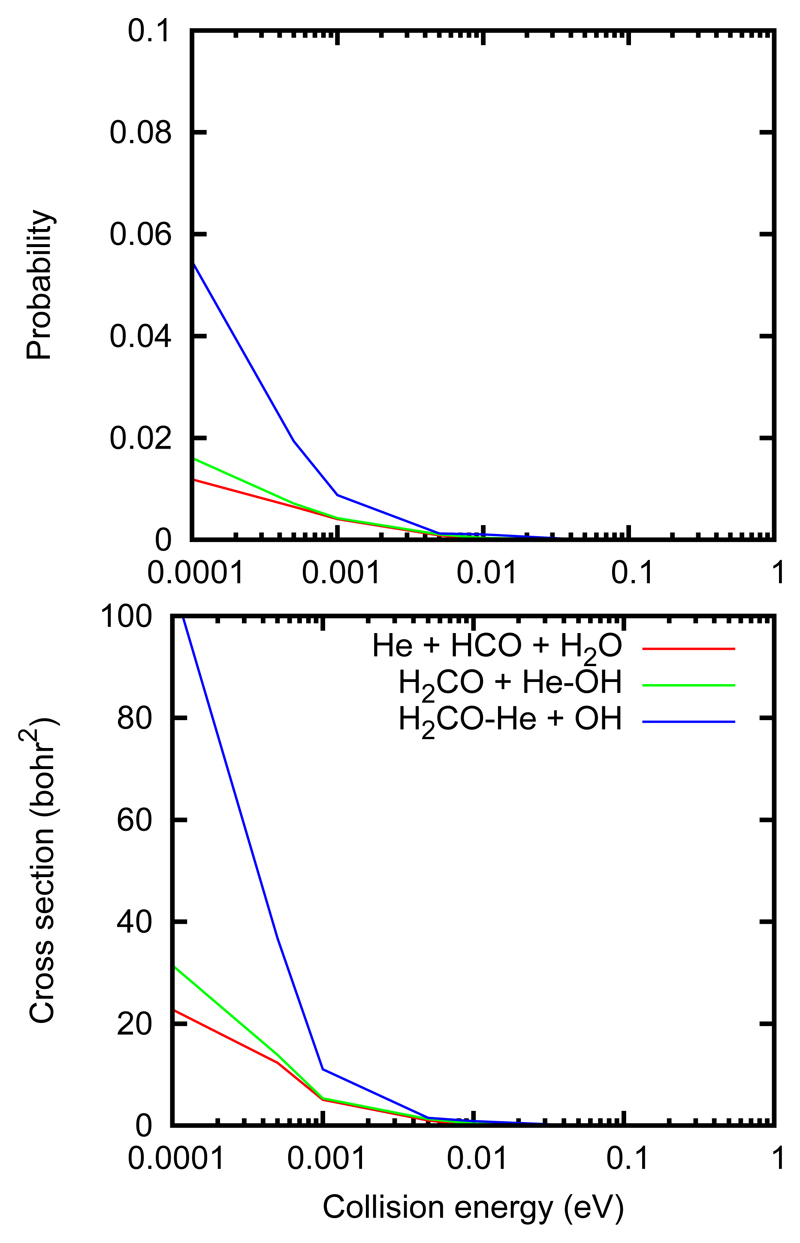
In the He + OH-H₂CO case, we can differentiate similar channels, namely

$$\begin{array}{ll}He+H_{2}CO\cdots OH\to H_{2}CO\cdots OH+He\hfill & \hfill \text{Inelastic}\\ \to H_{2}CO+OH+He\hfill & \hfill \text{Complex}\text{dissociation}\\ \to H_{2}CO+He\cdots OH\hfill & \hfill \text{He}–\text{exchange}\\ \to H_{2}CO\cdots He+OH\hfill & \hfill \text{Complex}\text{forming}\\ \to HCO+He+H_{2}O\hfill & \hfill \text{Reaction.}\end{array}$$ (5)

Because the long range interactions are weaker in this system, all the cross sections are considerably lower than in the previous case. The reaction cross section to form HCO products increases slightly with decreasing collision energy, and is smaller than that obtained in the He⋯ H₂CO + OH collisions. The fact that the cross sections for all processes in Fig. 10 increase with decreasing energy indicates that they are due to the formation of a complex in which there is an energy redistribution.

Figure 10.

QCT cross sections (bottom panel) and probability (top panel) for the processes of Eq. 5 in OH⋯ H₂CO + He collision.

The contribution of He + H₂CO⋯ OH and He⋯ H₂CO + OH to the reactivity depends not only on the cross sections but also on the densities of the parent complexes, which are also connected through the collisions. Therefore a realistic simulation of the experimental conditions such as density of the different species, temperatures, etc., are required. Moreover, quantum effects are also expected to play an important role, as in the H₂CO + OH collisions discussed above. For this reason we plan to perform a RPMD study of some of these reactive processes to shed light on these reactions.

5. Conclusions

In this work, we present a review for the Ring Polymer Molecular (RPMD) study of the reaction of OH with H₂CO and CH₃OH,⁴² showing the importance of the formation of very long-lived collision complex, COM-OH, below 100-200 K. These complexes live at least of the order of 0.1 μs, at 100 K, and it is expected to live even longer at lower temperatures. These long lifetimes are slightly shorter than average collision times at the conditions of the CRESU experiments (E. Jiménez, private communication) and supports the existence of pressure effects. However, the pure RPMD zero-pressure simulations⁴² are very close to the experimental data, suggesting that pressure effects do not strongly change the reactivity in these cases.

Since the most commonly used buffer gas in CRESU experiments is helium, we present a first dynamical study on the pressure effects. For this purpose, highly accurate potential energy surfaces (PESs) for He with all the reactants and products have been developed here. The PESs for the series of complexes involved (He-X, X = H₂CO, HCO, H₂O, OH), calculated at a uniform level of accuracy, show the anisotropy of interactions increasing with the system size. In particular, comparison of the He-X PES for X = H₂CO and HCO together with X = CO has indicated appearance of additional minima from the latter to the former. In addition, a consistent stabilization of these complexes with subsequent addition of H atoms is predicted, apparently due to increasing polarity of the molecules. Besides, the He-H₂CO PES features a lower anisotropy in the plane perpendicular to the molecule as compared to coplanar geometries, with the corresponding barriers between the two almost degenerate conformers, coplanar and axial (on the H side), different by a factor of two. In contrast, the situation is opposite for He-H₂O.

The calculated IR intensity spectra are sensitive indicators of the complexation, manifesting it via new lines corresponding to the interactions of components. Three strong lines have been identified for the OH-H₂CO complex, all dominated by the movements of OH. These spectra also reflect the strength of the interactions between the components, e.g., from weak lines for He-H₂CO to strong lines for OH-H₂CO. Still another factor is the mutual orientation of the components, affecting the relative line intensities for different modes of vibrations of one component relative to the other, such as of OH near H₂CO. In particular, the O-H stretch is found to produce the strongest line, more than an order of magnitude more intense than for the isolated diatom.

The stability of the He-H₂CO complexes is studied with the path integral molecular dynamics (PIMD) method, which allows to establish that these complexes are formed below 50 K. The OH-H₂CO collision complexes, however, survive more than 0.1 μs below 100-200 K, suggesting that different complexes can play an important role depending on the temperature range.

In addition, QCT calculations for the He-H₂CO + OH and OH-H₂CO + He collisions have been performed in this work, as a first preliminary check of their role played in the reaction under multiple collision conditions, or pressure effects. In the He-H₂CO + OH case, the reaction cross sections to form HCO + H₂O are more than 10 times higher than in the OH-H₂CO + He case at low collision energies. The reason is that long range dipole-dipole interaction is stronger as compared to the weak dispersion forces. Also, the OH-H₂CO complex is more stable than the He-H₂CO one, which thus may be broken more easily. For He-H₂CO + OH, the OH-H₂CO complex formation is facilitated by He, likely due to removal of excess kinetic energy and therefore stabilization of the complex, while the reaction leading to HCO + H₂O is hindered. The importance of the interactions with He should apparently multiply for analogous processes in helium clusters and nanodroplets. In particular, the above mentioned OH-CH₃OH complex was produced experimentally in a helium nanodroplet environment.⁵⁵ The presently studied OH-H₂CO could likely be formed in such a way as well.

Extending this study to all the processes and complexes may allow to perform a dynamical approach to pressure effects by calculating the individual collisional events and then solving the master equation to get the effective reaction rate constant. At the low temperatures of interest, below 100 K, quantum effects are important and should be included. Work in this direction, using the RPMD methodology is being done to analyze pressure effects.

In astrophysical environments the density is very low, and therefore only the zero-pressure reaction rate constants are of interest. The reviewed RPMD results in the zero-pressure limit are therefore important to show the increase of the rate below 100 K, very similar to the experimental results until ≈ 50 K for the two reactions studied. Since many reactions of COMs with OH have been reported, it is also very important to determine the effect of pressure on those measurements. Following the indications of the present results, these effects seem to be smaller than in the recent TST studies, and it is of paramount importance to analyze this problem in more detail.