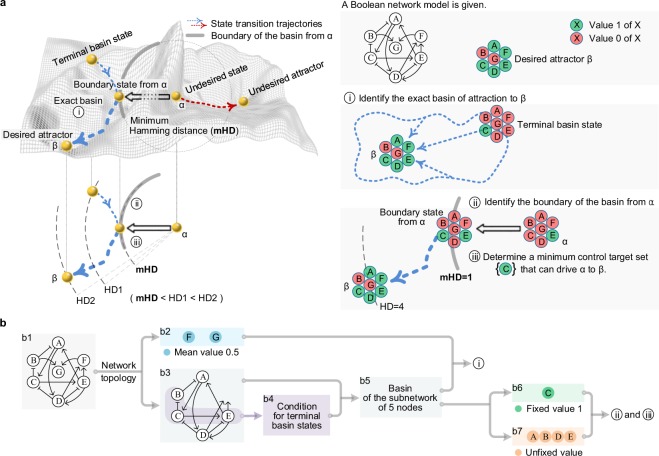
Figure 1.

Overview of BRC. (a) The overall flow of BRC process is illustrated in three steps. Given a Boolean network model (top right: arrows and bar-headed lines represent activation and inhibition, respectively) and a desired attractor state β (A, B, C, D, E, F, G) = (1, 0, 1, 1, 1, 1, 0), the first step $\overline{)\mathrm{i}}$ (middle right) is to identify the exact basin of β in a hierarchical and algebraic way, searching from β to the terminal states of state transition trajectories. So, the exact basin contains those states upon the state transition trajectory from the terminal state (0, 0, 1, 0, 0, 0, 0) to β, represented by two connected dotted blue arrows on the attractor landscape (left). The second step $\overline{)\mathrm{ii}}$ is to identify the boundary of the basin from an undesired state α converging to an undesired attractor where the convergence and the boundary are represented by the blue dotted arrow and the thick arc of a dotted circle in top left. The boundary consists of those states of having a minimum Hamming distance from α. Bottom left shows that a boundary state might not be a terminal state. The last step $\overline{)\mathrm{iii}}$ is to determine a boundary state to which α is to be driven and then a minimum control target set is determined, where all the leftward arrows denote driving α (0, 0, 0, 0, 1, 0, 0) to the boundary state (0, 0, 1, 0, 1, 0, 0) and thereby {C = 0} becomes the minimum control target set (bottom right). (b) The overall flow of the three steps is summarized. The first step $\overline{)\mathrm{i}}$ begins to divide the model (b1) into symmetric nodes F and G (b2) and a subnetwork of the remaining five nodes (b3). The topological and algebraic structures (B, C and E in purple) provide conditions for terminal states (b4), which are used to identify the basin of the reduced attractor β′ (A, B, C, D, E) = (1, 0, 1, 1, 1) in the subnetwork (b5). Concatenation of each basin state of β′ and all possible states of (F, G) results in the exact basin of β. The basin of β′ is decomposed into two collections b6 and b7 for $\overline{)\mathrm{ii}}$ and $\overline{)\mathrm{iii}}$. See Results, Supplementary Figs 1–3 and Methods for details.