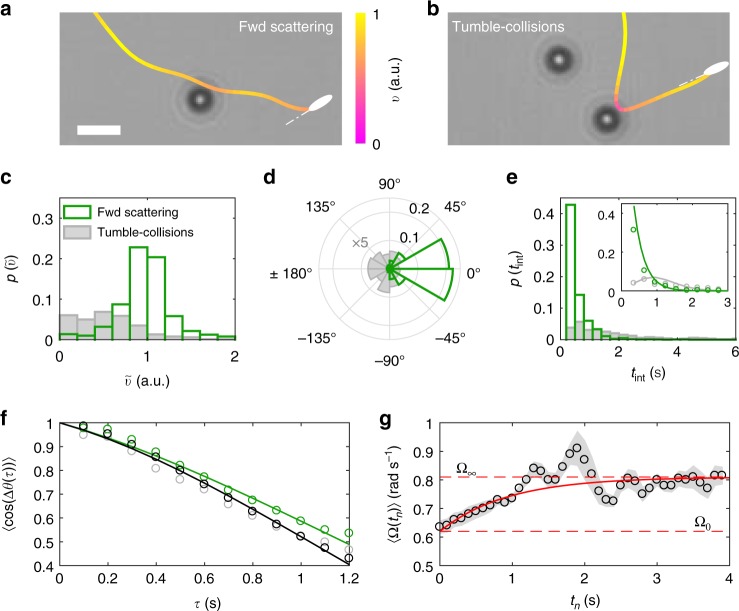
Fig. 3.

Differences between cell–obstacle interactions classified as forward scattering and tumble-collisions. a, b Examples of a forward-scattering event (a) and a tumble-collision (b). The stylised cells represent the trajectories’ final position and orientation. The trajectories’ colour code represents the cells’ normalised instantaneous velocity v. The white scale bar corresponds to 5 μm. c–e Probability density distributions of the cells’ c change in relative speed $ṽ$, d change in direction of motion Δθ_int, and e time t_int spent at the obstacles during interaction for forward scattering (empty histograms) and tumble-collisions (filled histograms). All distributions are normalised to the total number of interactions to show the relative weight between forward-scattering events and tumble-collisions. In d, the distribution for tumble-collisions is 5× bigger for visualisation. In the inset in e, the experimental distributions (circles) are fitted to an exponential distribution for forward scattering and to a Poissonian distribution for tumble-collisions (solid lines). f Average experimental decorrelation 〈cos(Δθ(τ))〉 of the cells’ direction of motion over time for forward scattering (green circles) and tumble-collisions (grey circles) calculated as ensemble average from the first instant t₀ after at least 100 cell–obstacle interactions. For reference, the black circles show the same quantity calculated in the absence of obstacles (Eq. (3), Methods). The solid lines are fittings to the function $f\left(\tau \right)=\cos \left(\mathrm{\Omega }\tau \right){\mathrm{e}}^{-\tau ∕{\tau }_0}$. g Time evolution of the cells’ average angular speed 〈Ω〉 (black circles) after the end of a forward-scattering event. Each value is calculated as an ensemble average from the n-th instant t_n after at least 100 forward-scattering events. The shaded area represents one standard deviation around the average values. The solid line represents the fitting to the function $f\left(t_n\right){=\mathrm{\Omega }}_{\infty }-\left({\mathrm{\Omega }}_{\infty }{-\mathrm{\Omega }}_0\right){\mathrm{e}}^{-t_n∕{\tau }_{\mathrm{\Omega }}}$, where Ω₀ and Ω_∞ (dashed lines) are the average angular speeds at t₀ and for ρ = 0%, respectively